3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997
Werbung

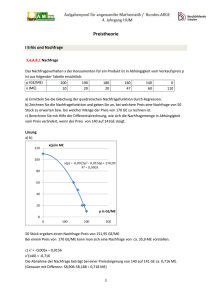
4. Lernzielkontrolle aus Mathematik und angewandte Mathematik 4 ak – 2014 - riegler Montag, 10. Juni 2013 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notation ist bewertungsrelevant und führt zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) b) 2. a) b) 3. a) b) 4. a) b) Die Elastizität einer Nachfrage läuft mit (x) = Error!. Bei einem Preis von 4 GE/ME können 2 ME Absatz erzielt werden. Berechnen Sie die Gleichung der Nachfragefunktion. (x) = Error! = – Error! Error! = Error! ln(p) = C + ln(x – 10) – ln(x) p = K Error! mit 4 = K (–4) K = –1 p(x) = Error! Eine Nachfragefunktion lautet: p(x) = 35 – 12x + x2. Berechnen Sie die Sättigungsmenge und den Prohibitivpreis. Berechnen Sie die Elastizität bei Menge von m Preis von 8 GE/ME. p(x) = 0 x = 5 und x = 7 relevant ist 5 daher Sättigungsmenge = 5 ME. p(0) = 35 daher Prohibitivpreis = 35 GE/ME 8 = 35 – 12x + x2 x = 3 Error! = 2x – 12 Error!(3) = –6 (3) = – Error! = 0,444 Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = 29 – 2x. Berechnen Sie die Stelle des maximalen Erlöses. (x) = 1 = 29 – 2x x = 14 Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = Error!. Berechnen Sie die Elastizität an der Stelle x = 20. Berechnen Sie, um welchen Prozentsatz sich die Nachfrage ändert, wenn der Preis um 10 % gesenkt wird. Berechnen Sie, um welchen Prozentsatz sich dann der Erlös ändert. (20) = 1,5 d.h. die Absatzänderung ist – 1,5 mal so hoch wie die Preisänderung, daher – 15 % der Erlös sinkt dann mit 0,85 · 1,1 = 0,935 um 6,5 % Eine quadratische Nachfragefunktion p(x) = ax2 + bx + c erfüllt folgende Bedingungen: Der Prohibitivpreis ist 150 GE/ME, bei einem Preis von 36 GE/ME können 6 ME verkauft werden. Die Elastizität bei diesem Preis ist Error!. Berechnen Sie die Nachfragefunktion. 150 = c 36 = 36a + 6b + c Error! = Error! 432a + 36b = –468 a = 1, b = – 25 c = 150 daher p(x) = x2 – 25x + 150 Ein Produkt hat folgende Nachfrage- und Angebotsfunktionen: p(x) = 100 – x und a(x) = 1 + 2x. Berechnen Sie den Gleichgewichtspreis. Berechnen Sie den Angebotsüberhang bei einem Preis von 81 GE/ME. 100 – x = 1 + 2x 99 = 3x x = 33 und p(33) = 67 = a(33) 81 = 100 – xn xn = 19 81 = 1 + 2xa xa = 40 daher x = 21 ME Der Gleichgewichtspreis ist 67 GE/ME, bei einem Preis von 81 GE/ME beträgt der Nachfrageüberhang 21 ME. Ein Betrieb hat einen linear-progressiven Kostenverlauf mit Fixkostensprung: Von 0 bis 10 ME verläuft der Kostenverlauf linear mit K 1(x) = 50 + 2x. Im Bereich zwischen 10 ME und 20 ME ist K2(x) = 1,4x2 – 26x + 190. Beim Beschäftigungsgrad 20 erfolgt ein Fixkostensprung über 100 GE. Berechnen Sie die Gleichung von K3(x) = ax + b im Bereich [20 / 40], wenn die neuen Grenzkosten nur mehr 1 GE/ME betragen. K3(20) = K2(20) + 100 = 330 330 = 20 + b b = 310 daher K3(x) = x + 310 Für: K1(x) = 50 + 4x für 0 ≤ x ≤ 10 K2(x) = 1,3x2 – 22x + 180 für 10 < x < 20 K3(x) = 2x + 270 für 20 ≤ x ≤ 40 und einem festen Verkaufspreis p = 10 GE/ME berechnen Sie den Gewinn an der Kapazitätsgrenze (d.h. bei x = 40. K(40) = 350 E(40) = 400 daher G(40) = 50 4. Lernzielkontrolle aus Mathematik und angewandte Mathematik 4 ak – 2014 - riegler Montag, 10. Juni 2013 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notation ist bewertungsrelevant und führt zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) b) 2. a) b) 3. a) b) 4. a) b) Die Elastizität einer Nachfrage läuft mit (x) = Error!. Bei einem Preis von 8 GE/ME können 2 ME Absatz erzielt werden. Berechnen Sie die Gleichung der Nachfragefunktion. (x) = Error! = – Error! Error! = Error! ln(p) = C + ln(x – 10) – ln(x) p = K Error! mit 8 = K (–4) K = –2 p(x) = Error! Eine Nachfragefunktion lautet: p(x) = 350 – 120x + 10x2. Berechnen Sie die Sättigungsmenge und den Prohibitivpreis. Berechnen Sie die Elastizität bei Menge von m Preis von 80 GE/ME. p(x) = 0 x = 5 und x = 7 relevant ist 5 daher Sättigungsmenge = 5 ME. p(0) = 350 daher Prohibitivpreis = 350 GE/ME 80 = 350 – 120x + 10x2 x = 3 Error! = 20x – 120 Error!(3) = –60 (3) = – Error! = 0,444 Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = 27 – 2x. Berechnen Sie die Stelle des maximalen Erlöses. (x) = 1 = 27 – 2x x = 13 Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = Error!. Berechnen Sie die Elastizität an der Stelle x = 20. Berechnen Sie, um welchen Prozentsatz sich die Nachfrage ändert, wenn der Preis um 10 % gesenkt wird. Berechnen Sie, um welchen Prozentsatz sich dann der Erlös ändert. (20) = 1,5 d.h. die Absatzänderung ist – 1,5 mal so hoch wie die Preisänderung, daher – 15 % der Erlös sinkt dann mit 0,85 · 1,1 = 0,935 um 6,5 % Eine quadratische Nachfragefunktion p(x) = ax2 + bx + c erfüllt folgende Bedingungen: Der Prohibitivpreis ist 150 GE/ME, bei einem Preis von 36 GE/ME können 6 ME verkauft werden. Die Elastizität bei diesem Preis ist Error!. Berechnen Sie die Nachfragefunktion. 150 = c 36 = 36a + 6b + c Error! = Error! 432a + 36b = –468 a = 1, b = – 25 c = 150 daher p(x) = x2 – 25x + 150 Ein Produkt hat folgende Nachfrage- und Angebotsfunktionen: p(x) = 100 – x und a(x) = 1 + 2x. Berechnen Sie den Gleichgewichtspreis. Berechnen Sie den Angebotsüberhang bei einem Preis von 81 GE/ME. 100 – x = 1 + 2x 99 = 3x x = 33 und p(33) = 67 = a(33) 81 = 100 – xn xn = 19 81 = 1 + 2xa xa = 40 daher x = 21 ME Der Gleichgewichtspreis ist 67 GE/ME, bei einem Preis von 81 GE/ME beträgt der Nachfrageüberhang 21 ME. Ein Betrieb hat einen linear-progressiven Kostenverlauf mit Fixkostensprung: Von 0 bis 10 ME verläuft der Kostenverlauf linear mit K 1(x) = 50 + 2x. Im Bereich zwischen 10 ME und 20 ME ist K2(x) = 1,4x2 – 26x + 190. Beim Beschäftigungsgrad 20 erfolgt ein Fixkostensprung über 100 GE. Berechnen Sie die Gleichung von K3(x) = ax + b im Bereich [20 / 40], wenn die neuen Grenzkosten nur mehr 1 GE/ME betragen. K3(20) = K2(20) + 100 = 330 330 = 20 + b b = 310 daher K3(x) = x + 310 Für: K1(x) = 50 + 4x für 0 ≤ x ≤ 10 K2(x) = 1,3x2 – 22x + 180 für 10 < x < 20 K3(x) = 2x + 270 für 20 ≤ x ≤ 40 und einem festen Verkaufspreis p = 10 GE/ME berechnen Sie den Gewinn an der Kapazitätsgrenze (d.h. bei x = 40. K(40) = 350 E(40) = 400 daher G(40) = 50 4. Lernzielkontrolle aus Mathematik und angewandte Mathematik 4 ak – 2014 - riegler Montag, 10. Juni 2013 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notation ist bewertungsrelevant und führt zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Die Elastizität einer Nachfrage läuft mit (x) = Error!. Bei einem Preis von 4 GE/ME können 2 ME Absatz erzielt werden. Berechnen Sie die Gleichung der Nachfragefunktion. b) Eine Nachfragefunktion lautet: p(x) = 35 – 12x + x2. Berechnen Sie die Sättigungsmenge und den Prohibitivpreis. Berechnen Sie die Elastizität bei Menge von m Preis von 8 GE/ME. a) Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = 29 – 2x. Berechnen Sie die Stelle des maximalen Erlöses. b) Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = Error!. Berechnen Sie die Elastizität an der Stelle x = 20. Berechnen Sie, um welchen Prozentsatz sich die Nachfrage ändert, wenn der Preis um 10 % gesenkt wird. Berechnen Sie, um welchen Prozentsatz sich dann der Erlös ändert. a) Eine quadratische Nachfragefunktion p(x) = ax2 + bx + c erfüllt folgende Bedingungen: Der Prohibitivpreis ist 150 GE/ME, bei einem Preis von 36 GE/ME können 6 ME verkauft werden. Die Elastizität bei diesem Preis ist Error!. Berechnen Sie die Nachfragefunktion. b) Ein Produkt hat folgende Nachfrage- und Angebotsfunktionen: p(x) = 100 – x und a(x) = 1 + 2x. Berechnen Sie den Gleichgewichtspreis. Berechnen Sie den Angebotsüberhang bei einem Preis von 81 GE/ME. a) Ein Betrieb hat einen linear-progressiven Kostenverlauf mit Fixkostensprung: Von 0 bis 10 ME verläuft der Kostenverlauf linear mit K1(x) = 50 + 2x. Im Bereich zwischen 10 ME und 20 ME ist K2(x) = 1,4x2 – 26x + 190. Beim Beschäftigungsgrad 20 erfolgt ein Fixkostensprung über 100 GE. Berechnen Sie die Gleichung von K3(x) = ax + b im Bereich [20 / 40], wenn die neuen Grenzkosten nur mehr 1 GE/ME betragen. b) Für: K1(x) = 50 + 4x für 0 ≤ x ≤ 10 K2(x) = 1,3x2 – 22x + 180 für 10 < x < 20 K3(x) = 2x + 270 für 20 ≤ x ≤ 40 und einem festen Verkaufspreis p = 10 GE/ME berechnen Sie den Gewinn an der Kapazitätsgrenze (d.h. bei x = 40. 4. Lernzielkontrolle aus Mathematik und angewandte Mathematik 4 ak – 2014 - riegler Montag, 10. Juni 2013 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notation ist bewertungsrelevant und führt zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. 2. 3. 4. a) Die Elastizität einer Nachfrage läuft mit (x) = Error!. Bei einem Preis von 8 GE/ME können 2 ME Absatz erzielt werden. Berechnen Sie die Gleichung der Nachfragefunktion. b) Eine Nachfragefunktion lautet: p(x) = 350 – 120x + 10x2. Berechnen Sie die Sättigungsmenge und den Prohibitivpreis. Berechnen Sie die Elastizität bei Menge von m Preis von 80 GE/ME. a) Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = 27 – 2x. Berechnen Sie die Stelle des maximalen Erlöses. b) Der Verlauf der Elastizität für eine Nachfragefunktion ist (x) = Error!. Berechnen Sie die Elastizität an der Stelle x = 20. Berechnen Sie, um welchen Prozentsatz sich die Nachfrage ändert, wenn der Preis um 10 % gesenkt wird. Berechnen Sie, um welchen Prozentsatz sich dann der Erlös ändert. a) Eine quadratische Nachfragefunktion p(x) = ax2 + bx + c erfüllt folgende Bedingungen: Der Prohibitivpreis ist 150 GE/ME, bei einem Preis von 36 GE/ME können 6 ME verkauft werden. Die Elastizität bei diesem Preis ist Error!. Berechnen Sie die Nachfragefunktion. b) Ein Produkt hat folgende Nachfrage- und Angebotsfunktionen: p(x) = 100 – x und a(x) = 1 + 2x. Berechnen Sie den Gleichgewichtspreis. Berechnen Sie den Angebotsüberhang bei einem Preis von 81 GE/ME. a) Ein Betrieb hat einen linear-progressiven Kostenverlauf mit Fixkostensprung: Von 0 bis 10 ME verläuft der Kostenverlauf linear mit K 1(x) = 50 + 2x. Im Bereich zwischen 10 ME und 20 ME ist K2(x) = 1,4x2 – 26x + 190. Beim Beschäftigungsgrad 20 erfolgt ein Fixkostensprung über 100 GE. Berechnen Sie die Gleichung von K3(x) = ax + b im Bereich [20 / 40], wenn die neuen Grenzkosten nur mehr 1 GE/ME betragen. b) Für: K1(x) = 50 + 4x für 0 ≤ x ≤ 10 K2(x) = 1,3x2 – 22x + 180 für 10 < x < 20 K3(x) = 2x + 270 für 20 ≤ x ≤ 40 und einem festen Verkaufspreis p = 10 GE/ME berechnen Sie den Gewinn an der Kapazitätsgrenze (d.h. bei x = 40.