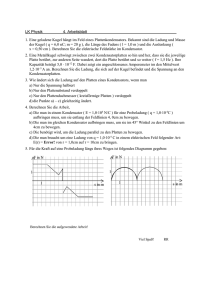
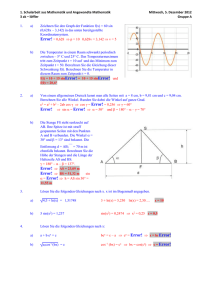
3. Schriftliche Wiederholung aus Physik Donnerstag, 27. Februar 1997
Werbung

1. Schularbeit aus Mathematik und angewandter Mathematik 4 ck - lunzer ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Dienstag, 29. November 2016 Gruppe A Name: - Zeigen Sie allgemein, dass die Folge ⟨an⟩ = Error!streng monoton fallend ist. - Geben Sie den Grenzwert der Folge an - Geben Sie den Index des Folgengliedes an, dass sich um weniger als 0,03 vom Grenzwert unterscheidet. Error! < Error! (3n + 12) (n + 1) < (3n + 9) (n + 2) 3n2 + 15n + 12 < 3n2 + 15n + 18 richtig für alle n ∈ ℕ lim; n→∞ Error! = Error!Error! = 3 3,03 > Error! 3,03n + 3,03 > 3n + 9 0,03n > 5,97 n > 199 also a200 = 3,02985 . 2. b) - Argumentieren Sie, warum die Folge ⟨dn⟩ = Error!eine geometrische Folge ist. - Berechnen Sie die Summe der ersten 10 Folgenglieder. - Berechnen Sie die Summe aller Folgenglieder s . weil der Quotient Error! = –0,2 immer gleich groß ist. s20 = 3 125 Error! = 2 604,1664 s = Error! = 2.604,1666… a) Von einer Funktion f(x) kennt man f(10) = 100, f(5) = 25, f(7) = 49 und die Werte der Differentialquotienten Error!(10) = 20, Error!(5) = 10, Error!(7) = 14 Berechnen Sie näherungsweise den Funktionswert f(7,03) und f(9). Begründen Sie, warum f(9) viel ungenauer als f(7,03) wird. Error!(7) = 14 Error! f(7,03) = 14 · 0,03 + 49 = 49,42 Error!(10) = 20 Error! f(9) = 20 · (–1) + 100 = 80 x ist hier viel größer, daher ungenauer b) Ein Gefäß wird im Rahmen einer Produktion mit Flüssigkeit gefüllt. Die Gesamtmenge im Gefäß wird durch die Funktion G(t) beschrieben. G ist die Menge in Liter (L), t die Zeit seit Beginn der Füllung in Minuten (min). - Beschreiben Sie, was die Werte G(10) = 350 und G′(7) = 15 im Sachzusammenhang bedeuten. - Erläutern Sie, was G′(7) = 15 für den Graphen der Funktion G(t) in einem Koordinatensystem bedeutet. G(10) = 350 heißt, dass nach 10 Minuten die Füllmenge 350 L beträgt G′(7) = 15 heißt, dass zum Zeitpunkt 7 die zufließende Menge 15 L/min beträgt. G′(7) = 15 gibt die Steigung der Tangente im Punkt mit dem t-Wert 7 an. A 3. 4 a) - Berechnen Sie für die Funktion f(a,b) = ab 3 + eb – sin(a) Error!= b3 – cos(a) Error!= 3ab2 + eb b) - Differenzieren und vereinfachen Sie: y = 5x2 e–2x. y‘ = 10x e–2x + 5x2 (–2) e–2x = 10x e–2x (1 – x) c) - Differenzieren und vereinfachen Sie: y = Error! y‘ = Error! = Error! a) Ein von einer erhöhten Plattform hochgeworfener Körper bewegt sich mit der Bewegungsgleichung h(t) = 20 + 4t – 5t2. h ist dabei die Höhe über Grund in Meter (m), t die Zeit nach Abwurf in Sekunden (s). - Berechnen Sie die Abwurfhöhe - Berechnen Sie die Abwurfgeschwindigkeit - Geben Sie ein Verfahren an, wie man die Aufprallgeschwindigkeit auf dem Boden berechnen kann. Error! und dann Error! h(0) = 20 v = Error! = 4 – 10t v(0) = 4 m/s zuerst den Aufprallzeitpunkt p mit h(t) = 0 berechnen, dann p in v einsetzen. . b) Ein Fahrzeug bewegt sich mit gleichbleibender Beschleunigung von 0,6 m/s2 in positiver s-Richtung und hat nach 10 s die Geschwindigkeit 11 m/s. Der Startpunkt der Bewegung erfolgt bei s = 0. Die allgemeine Bewegungsgleichung ist s(t) = at2 + bt + c Geben Sie ein Gleichungssystem in a, b und c an, mit dem man die Werte von a, b und c bestimmen kann. v = s ′ = 2at + b a = v ′ = s ″ = 2a 2a = 0,6 und 11 = v(10) = 20a + b und s(0) = 0 = c 1. Schularbeit aus Mathematik und angewandter Mathematik 4 ck - lunzer ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Dienstag, 29. November 2016 Gruppe B Name: - Zeigen Sie allgemein, dass die Folge ⟨an⟩ = Error!streng monoton fallend ist. - Geben Sie den Grenzwert der Folge an - Geben Sie den Index des Folgengliedes an, dass sich um weniger als 0,03 vom Grenzwert unterscheidet. Error! < Error! (4n + 13) (n + 1) < (4n + 9) (n + 2) 4n2 + 17n + 13 < 4n2 + 17n + 18 richtig für alle n ∈ ℕ lim; n→∞ Error! = Error!Error! = 4 4,03 > Error! 4,03n + 4,03 > 4n + 9 0,03n > 4,97 n > 165,67 also a166 = 4,0299 . 2. b) - Argumentieren Sie, warum die Folge ⟨dn⟩ = Error!eine geometrische Folge ist. - Berechnen Sie die Summe der ersten 10 Folgenglieder. - Berechnen Sie die Summe aller Folgenglieder s . weil der Quotient Error! = –0,8 immer gleich groß ist. s20 = 1 000 Error! = 495,9 s = Error! = 555,55… a) Von einer Funktion f(x) kennt man f(10) = 200, f(5) = 50, f(7) = 98 und die Werte der Differentialquotienten Error!(10) = 40, Error!(5) = 20, Error!(7) = 28 Berechnen Sie näherungsweise den Funktionswert f(7,03) und f(9). Begründen Sie, warum f(9) viel ungenauer als f(7,03) wird. Error!(7) = f28 Error! f(7,03) = 28 · 0,03 + 98 = 98,84 Error!(10) = 40 Error! f(9) = 40 · (–1) + 200 = 160 x ist hier viel größer, daher ungenauer b) Ein Gefäß wird im Rahmen einer Produktion mit Flüssigkeit gefüllt. Die Gesamtmenge im Gefäß wird durch die Funktion G(t) beschrieben. G ist die Menge in Liter (L), t die Zeit seit Beginn der Füllung in Minuten (min). - Beschreiben Sie, was die Werte G(10) = 700 und G′(7) = 30 im Sachzusammenhang bedeuten. - Erläutern Sie, was G′(7) = 30 für den Graphen der Funktion G(t) in einem Koordinatensystem bedeutet. G(10) = 700 heißt, dass nach 10 Minuten die Füllmenge 700 L beträgt G′(7) = 30 heißt, dass zum Zeitpunkt 7 die zufließende Menge 30 L/min beträgt. G′(7) = 30 gibt die Steigung der Tangente im Punkt mit dem t-Wert 7 an. A 3. 4 a) - Berechnen Sie für die Funktion f(a,b) = a3b + ea – sin(b) Error!= 3a2b + ea Error!= a3 – cos(b) b) - Differenzieren und vereinfachen Sie: y = 6x2 e–2x. y‘ = 12x e–2x + 6x2 (–2) e–2x = 12x e–2x (1 – x) c) - Differenzieren und vereinfachen Sie: y = Error! y‘ = Error! = Error! a) Ein von einer erhöhten Plattform hochgeworfener Körper bewegt sich mit der Bewegungsgleichung h(t) = 10 + 6t – 5t2. h ist dabei die Höhe über Grund in Meter (m), t die Zeit nach Abwurf in Sekunden (s). - Berechnen Sie die Abwurfhöhe - Berechnen Sie die Abwurfgeschwindigkeit - Geben Sie ein Verfahren an, wie man die Aufprallgeschwindigkeit auf dem Boden berechnen kann. Error! und dann Error! h(0) = 10 v = Error! = 4 – 10t v(0) = 6 m/s zuerst den Aufprallzeitpunkt p mit h(t) = 0 berechnen, dann p in v einsetzen. . b) Ein Fahrzeug bewegt sich mit gleichbleibender Beschleunigung von 0,6 m/s 2 in positiver s-Richtung und hat nach 5 s die Geschwindigkeit 8 m/s. Der Startpunkt der Bewegung erfolgt bei s = 0. Die allgemeine Bewegungsgleichung ist s(t) = at2 + bt + c Geben Sie ein Gleichungssystem in a, b und c an, mit dem man die Werte von a, b und c bestimmen kann. v = s ′ = 2at + b a = v ′ = s ″ = 2a 2a = 0,6 und 8 = v(5) = 10a + b und s(0) = 0 = c 1. Schularbeit aus Mathematik und angewandter Mathematik 4 ck - lunzer ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. Dienstag, 29. November 2016 Gruppe A Name: a) - Zeigen Sie allgemein, dass die Folge ⟨an⟩ = Error!streng monoton fallend ist. - Geben Sie den Grenzwert der Folge an - Geben Sie den Index des Folgengliedes an, dass sich um weniger als 0,03 vom Grenzwert unterscheidet. b) - Argumentieren Sie, warum die Folge ⟨dn⟩ = Error!eine geometrische Folge ist. - Berechnen Sie die Summe der ersten 10 Folgenglieder. - Berechnen Sie die Summe aller Folgenglieder s . . A 2. a) Von einer Funktion f(x) kennt man f(10) = 100, f(5) = 25, f(7) = 49 und die Werte der Differentialquotienten Error!(10) = 20, Error!(5) = 10, Error!(7) = 14 Berechnen Sie näherungsweise den Funktionswert f(7,03) und f(9). Begründen Sie, warum f(9) viel ungenauer als f(7,03) wird. b) Ein Gefäß wird im Rahmen einer Produktion mit Flüssigkeit gefüllt. Die Gesamtmenge im Gefäß wird durch die Funktion G(t) beschrieben. G ist die Menge in Liter (L), t die Zeit seit Beginn der Füllung in Minuten (min). - Beschreiben Sie, was die Werte G(10) = 350 und G′(7) = 15 im Sachzusammenhang bedeuten. - Erläutern Sie, was G′(7) = 15 für den Graphen der Funktion G(t) in einem Koordinatensystem bedeutet. A 3. a) - Berechnen Sie für die Funktion f(a,b) = ab 3 + eb – sin(a) b) - Differenzieren und vereinfachen Sie: y = 5x2 e–2x. c) - Differenzieren und vereinfachen Sie: y = Error! 4 a) Ein von einer erhöhten Plattform hochgeworfener Körper bewegt sich mit der Bewegungsgleichung h(t) = 20 + 4t – 5t2. h ist dabei die Höhe über Grund in Meter (m), t die Zeit nach Abwurf in Sekunden (s). - Berechnen Sie die Abwurfhöhe - Berechnen Sie die Abwurfgeschwindigkeit - Geben Sie ein Verfahren an, wie man die Aufprallgeschwindigkeit auf dem Boden berechnen kann. . b) Ein Fahrzeug bewegt sich mit gleichbleibender Beschleunigung von 0,6 m/s 2 in positiver s-Richtung und hat nach 10 s die Geschwindigkeit 11 m/s. Der Startpunkt der Bewegung erfolgt bei s = 0. Die allgemeine Bewegungsgleichung ist s(t) = at2 + bt + c Geben Sie ein Gleichungssystem in a, b und c an, mit dem man die Werte von a, b und c bestimmen kann. Error! und dann Error! 1. Schularbeit aus Mathematik und angewandter Mathematik 4 ck - lunzer ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. Dienstag, 29. November 2016 Gruppe B Name: a) - Zeigen Sie allgemein, dass die Folge ⟨an⟩ = Error!streng monoton fallend ist. - Geben Sie den Grenzwert der Folge an - Geben Sie den Index des Folgengliedes an, dass sich um weniger als 0,03 vom Grenzwert unterscheidet. b) - Argumentieren Sie, warum die Folge ⟨dn⟩ = Error!eine geometrische Folge ist. - Berechnen Sie die Summe der ersten 10 Folgenglieder. - Berechnen Sie die Summe aller Folgenglieder s . . B 2. a) Von einer Funktion f(x) kennt man f(10) = 200, f(5) = 50, f(7) = 98 und die Werte der Differentialquotienten Error!(10) = 40, Error!(5) = 20, Error!(7) = 28 Berechnen Sie näherungsweise den Funktionswert f(7,03) und f(9). Begründen Sie, warum f(9) viel ungenauer als f(7,03) wird. b) Ein Gefäß wird im Rahmen einer Produktion mit Flüssigkeit gefüllt. Die Gesamtmenge im Gefäß wird durch die Funktion G(t) beschrieben. G ist die Menge in Liter (L), t die Zeit seit Beginn der Füllung in Minuten (min). - Beschreiben Sie, was die Werte G(10) = 700 und G′(7) = 30 im Sachzusammenhang bedeuten. - Erläutern Sie, was G′(7) = 30 für den Graphen der Funktion G(t) in einem Koordinatensystem bedeutet. B 3. a) - Berechnen Sie für die Funktion f(a,b) = a3b + ea – sin(b) b) - Differenzieren und vereinfachen Sie: y = 6x2 e–2x. c) - Differenzieren und vereinfachen Sie: y = Error! 4 a) Ein von einer erhöhten Plattform hochgeworfener Körper bewegt sich mit der Bewegungsgleichung h(t) = 10 + 6t – 5t2. h ist dabei die Höhe über Grund in Meter (m), t die Zeit nach Abwurf in Sekunden (s). - Berechnen Sie die Abwurfhöhe - Berechnen Sie die Abwurfgeschwindigkeit - Geben Sie ein Verfahren an, wie man die Aufprallgeschwindigkeit auf dem Boden berechnen kann. . b) Ein Fahrzeug bewegt sich mit gleichbleibender Beschleunigung von 0,6 m/s 2 in positiver s-Richtung und hat nach 5 s die Geschwindigkeit 8 m/s. Der Startpunkt der Bewegung erfolgt bei s = 0. Die allgemeine Bewegungsgleichung ist s(t) = at2 + bt + c Geben Sie ein Gleichungssystem in a, b und c an, mit dem man die Werte von a, b und c bestimmen kann. Error! und dann Error!