4. SA
Werbung

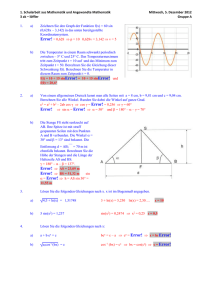
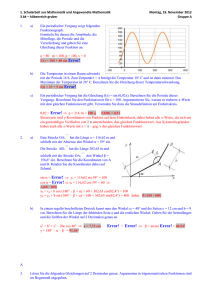
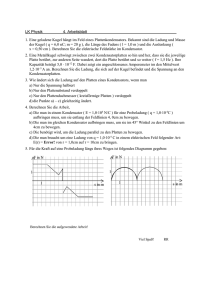
4. Schularbeit aus Mathematik und angewandter Mathematik 1al – kirisits Donnerstag, 7. Mai 2015 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) b) c) 2. 3. 4. Von einem allgemeinen Dreieck mit Standardbeschriftung kennt man: a = 12 cm, = 40° und γ = 75°. Berechnen Sie die Längen von b und c und die Größe des Winkels . = 180° – – γ = 65° Error! = Error! b = Error! = 16,92 cm Error! = Error! c = Error! = 18,03 cm Ein standardbeschriftetes allgemeines Dreieck hat die Seitenlängen a = 10 m, b = 15 m und die Fläche 44,08 m2. Berechnen Sie die Größe des Winkels γ . A = Error! sin γ = Error! = 0,5877… γ = 36° Ein viereckiges Grundstück (s. Skizze) hat folgende Form und Abmessungen. x sin φ = Error! Drei der fünf Gleichungen sind e2 = c2 + b2 – 2cb cos korrekt. Kreuzen Sie die x Error! = Error! zutreffenden Gleichungen an. + φ = 90° x b 2 + c2 = e2 a) Ermitteln Sie für die Funktion f(x) = 5 + 20 sin Error! die Periode und die Amplitude. Geben sie den maximalen und minimalen Funktionswert an. Periode = 50, Amplitude = 20, Max = 25 Min = –15 b) Zeichnen Sie den Funktionsverlauf von y = 10 sin Error! für 0 ≤ x ≤ 40 in das folgende Koordinatensystem ein: c) Zeichnen Sie in die Einheitskreisskizze den Winkel = 40° ein und ermitteln Sie einen weiteren Winkel im Bereich [0 ; 360°], der den gleichen Kosinuswert hat. Lesen Sie den cos(40°) so genau wie möglich ab. cos(40°) 0,76 = cos(320°) Lösen Sie die Gleichung 3x2 – 36x + 105 = 0 über ℝ. x1,2 = Error! = Error! x1 = 7 und x2 = 5 b) Ermitteln Sie in der Gleichung 5x2 +bx + 80 den Parameter b so, dass die Gleichung genau eine Lösung hat. b2 – 4 · 5 · 80 = 0 b2 = 1 600 b = ± 40 c) Eine quadratische Funktion hat die Nullstellen x1 = 7 und x2 = –3 und es gilt f(10) = 390. Berechnen Sie die Gleichung dieser Funktion. y = a(x – 7) (x + 3) mit 390 = a 3 · 13 a = 10 daher y = 10 (x – 7) (x + 3) = 10x2 – 40x – 210 Die Flugbahn eines Körpers wird durch die Funktion h(x) = –x2 +8x + 20 beschrieben. x ist die horizontale Entfernung in Meter (m) vom Abschussort, h(x) die Höhe über dem Boden in Meter an der Stelle x. a) Berechnen Sie aus welcher Höhe der Körper abgeschossen wurde. h(0) = 20 b) Berechnen Sie die Koordinaten des höchsten Punktes. h(x) = – (x2 – 8x) + 20 = – (x – 4)2 + 16 + 20 = – (x – 4)2 + 36 also S(4 / 36) c) Berechnen Sie, in welcher horizontalen Entfernung vom Abschusspunkt der Körper zum erstenmal den Boden berührt. h(x) = 0 = –x2 + 8x + 20 0 = x2 – 8x – 20 x12 = Error! x1 = 10 und x2 = –2 also nach 10 m a) 4. Schularbeit aus Mathematik und angewandter Mathematik 1al – kirisits Donnerstag, 7. Mai 2015 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) b) c) 2. a) b) c) 3. a) b) c) 4. Von einem allgemeinen Dreieck mit Standardbeschriftung kennt man: a = 120 cm, = 40° und γ = 75°. Berechnen Sie die Längen von b und c und die Größe des Winkels . = 180° – – γ = 65° Error! = Error! b = Error! = 169,2 cm Error! = Error! c = Error! = 180,3 cm Ein standardbeschriftetes allgemeines Dreieck hat die Seitenlängen a = 10 m, b = 5 m und die Fläche 18 m2. Berechnen Sie die Größe des Winkels γ . A = Error! sin γ = Error! = 0,72 γ = 46° Ein viereckiges Grundstück (s. Skizze) sin φ = Error! hat folgende Form und Abmessungen. e2 = c2 + b2 – 2cb cos γ x Drei der fünf Gleichungen sind korrekt. x Error! = Error! Kreuzen Sie die zutreffenden Gleichungen an. + φ = 90° x b 2 + c2 = e2 Ermitteln Sie für die Funktion f(x) = 7 + 30 sin Error! die Periode und die Amplitude. Geben sie den maximalen und minimalen Funktionswert an. Periode = 20, Amplitude = 30, Max = 37 Min = –23 Zeichnen Sie den Funktionsverlauf von y = 10 sin Error!für 0 ≤ x ≤ 40 in das folgende Koordinatensystem ein: Zeichnen Sie in die Einheitskreisskizze den Winkel = 40° ein und ermitteln Sie einen weiteren Winkel im Bereich [0 ; 360°], der den gleichen Sinuswert hat. Lesen Sie den sin(40°) so genau wie möglich ab. sin(40°) 0,64 = sin(140°) Lösen Sie die Gleichung 3x2 – 30x + 63 = 0 über ℝ. x1,2 = Error! = Error! x1 = 7 und x2 = 3 Ermitteln Sie in der Gleichung 2x2 +bx + 32 den Parameter b so, dass die Gleichung genau eine Lösung hat. b2 – 4 · 2 · 32 = 0 b2 = 256 b = ± 16 Eine quadratische Funktion hat die Nullstellen x1 = 7 und x2 = –3 und es gilt f(10) = 195. Berechnen Sie die Gleichung dieser Funktion. y = a(x – 7) (x + 3) mit 195 = a 3 · 13 a = 5 daher y = 5 (x – 7) (x + 3) = 5x2 – 20x – 105 Die Flugbahn eines Körpers wird durch die Funktion h(x) = –x2 +6x + 16 beschrieben. x ist die horizontale Entfernung in Meter (m) vom Abschussort, h(x) die Höhe über dem Boden in Meter an der Stelle x. a) b) c) Berechnen Sie aus welcher Höhe der Körper abgeschossen wurde. h(0) = 16 Berechnen Sie die Koordinaten des höchsten Punktes. h(x) = – (x2 – 6x) + 16 = – (x – 3)2 + 9 + 16 = – (x – 3)2 + 25 also S(3 / 25) Berechnen Sie, in welcher horizontalen Entfernung vom Abschusspunkt der Körper zum erstenmal den Boden berührt. h(x) = 0 = –x2 + 6x + 16 0 = x2 – 6x – 16 x12 = Error! x1 = 8 und x2 = –2 also nach 8 m 4. Schularbeit aus Mathematik und angewandter Mathematik 1al – kirisits Donnerstag, 7. Mai 2015 Gruppe A ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Von einem allgemeinen Dreieck mit Standardbeschriftung kennt man: a = 12 cm, = 40° und γ = 75°. Berechnen Sie die Längen von b und c und die Größe des Winkels . b) Ein standardbeschriftetes allgemeines Dreieck hat die Seitenlängen a = 10 m, b = 15 m und die Fläche 44,08 m2. Berechnen Sie die Größe des Winkels γ . c) Ein viereckiges Grundstück (s. Skizze) hat folgende Form und Abmessungen. Drei der fünf Gleichungen sind korrekt. Kreuzen Sie die zutreffenden Gleichungen an. sin φ = Error! e2 = c2 + b2 – 2cb cos Error! = Error! + φ = 90° b 2 + c2 = e2 2. a) Ermitteln Sie für die Funktion f(x) = 5 + 20 sin Error! die Periode und die Amplitude. Geben sie den maximalen und minimalen Funktionswert an. b) Zeichnen Sie den Funktionsverlauf von y = 10 sin Error!für 0 ≤ x ≤ 40 in das folgende Koordinatensystem ein: A 3. 4. c) Zeichnen Sie in die Einheitskreisskizze den Winkel = 40° ein und ermitteln Sie einen weiteren Winkel im Bereich [0 ; 360°], der den gleichen Kosinuswert hat. Lesen Sie den cos(40°) so genau wie möglich ab. Argumentieren Sie Ihre Vorgangsweise. a) Lösen Sie die Gleichung 3x2 – 36x + 105 = 0 über ℝ. b) Ermitteln Sie in der Gleichung 5x2 +bx + 80 den Parameter b so, dass die Gleichung genau eine Lösung hat. c) Eine quadratische Funktion hat die Nullstellen x1 = 7 und x2 = –3 und es gilt f(10) = 390. Berechnen Sie die Gleichung dieser Funktion. Die Flugbahn eines Körpers wird durch die Funktion h(x) = –x2 +8x + 20 beschrieben. x ist die horizontale Entfernung in Meter (m) vom Abschussort, h(x) die Höhe über dem Boden in Meter an der Stelle x. a) Berechnen Sie aus welcher Höhe der Körper abgeschossen wurde. b) Berechnen Sie die Koordinaten des höchsten Punktes. c) Berechnen Sie, in welcher horizontalen Entfernung vom Abschusspunkt der Körper zum erstenmal den Boden berührt. 4. Schularbeit aus Mathematik und angewandter Mathematik 1al – kirisits Donnerstag, 7. Mai 2015 Gruppe B ACHTUNG: Fehlerhafte und unübliche Notationen sind bewertungsrelevant und führen zu Punkteabzügen. Beantworten Sie Anwendungsbeispiele in ganzen Sätzen. Dokumentieren Sie Lösungswege (Ansätze, Nebenrechnungen, Überlegungen) 1. a) Von einem allgemeinen Dreieck mit Standardbeschriftung kennt man: a = 120 cm, = 40° und γ = 75°. Berechnen Sie die Längen von b und c und die Größe des Winkels . b) Ein standardbeschriftetes allgemeines Dreieck hat die Seitenlängen a = 10 m, b = 5 m und die Fläche 18 m2. Berechnen Sie die Größe des Winkels γ . c) Ein viereckiges Grundstück (s. Skizze) hat folgende Form und Abmessungen. Drei der fünf Gleichungen sind korrekt. Kreuzen Sie die zutreffenden Gleichungen an. sin φ = Error! e2 = c2 + b2 – 2cb cos γ Error! = Error! + φ = 90° b 2 + c2 = e2 2. a) Ermitteln Sie für die Funktion f(x) = 7 + 30 sin Error! die Periode und die Amplitude. Geben sie den maximalen und minimalen Funktionswert an. b) Zeichnen Sie den Funktionsverlauf von y = 10 sin Error!für 0 ≤ x ≤ 40 in das folgende Koordinatensystem ein: B 3. 4. c) Zeichnen Sie in die Einheitskreisskizze den Winkel = 40° ein und ermitteln Sie einen weiteren Winkel im Bereich [0 ; 360°], der den gleichen Sinuswert hat. Lesen Sie den sin(40°) so genau wie möglich ab. a) Lösen Sie die Gleichung 3x2 – 30x + 63 = 0 über ℝ. b) Ermitteln Sie in der Gleichung 2x2 +bx + 32 den Parameter b so, dass die Gleichung genau eine Lösung hat. c) Eine quadratische Funktion hat die Nullstellen x1 = 7 und x2 = –3 und es gilt f(10) = 195. Berechnen Sie die Gleichung dieser Funktion. Die Flugbahn eines Körpers wird durch die Funktion h(x) = –x2 +6x + 16 beschrieben. x ist die horizontale Entfernung in Meter (m) vom Abschussort, h(x) die Höhe über dem Boden in Meter an der Stelle x. a) Berechnen Sie aus welcher Höhe der Körper abgeschossen wurde. b) Berechnen Sie die Koordinaten des höchsten Punktes. c) Berechnen Sie, in welcher horizontalen Entfernung vom Abschusspunkt der Körper zum erstenmal den Boden berührt.