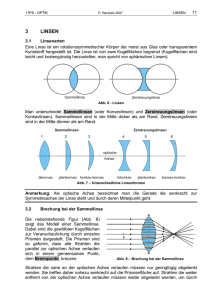
1 LICHT
Werbung

11PS – PHYSIK P. Rendulić 2014 OPTIK 1 OPTIK Die Optik ist ein Teilgebiet der Physik. Sie handelt vom Licht und vom Sehen. 1 1.1 LICHT Lichtquellen und beleuchtete Körper Sichtbare Körper senden teilweise Licht aus, teilweise reflektieren sie aber auch das auf sie fallende Licht. Beispiele für Lichtquellen Unsere Sonne ist für die Erde ein Im Universum gibt es Milliarden Ein Blitz ist eine Funkenentladung wichtiger Energieund von Sternen (das Bild zeigt den während eines Gewitters infolge Lichtlieferant. Sternhaufen der Plejaden, M45). einer elektrostatischen Entladung. Ein stromdurchflossener, Die Leuchtdiode (LED, light Eine Flamme besteht aus heissen, glühender Draht strahlt Licht aus emitting diode) ist seit einigen glühenden Verbrennungsabgasen. (hier: Glühwendel einer Lampe). Jahren, durch ihren geringen Energieverbrauch, eine immer wichtigere Lichtquelle. Beispiele für beleuchtete Körper Der Mond und die Planeten (rechts: Saturn, aufgenommen von der Alle sichtbaren Körper, die keine Raumsonde Voyager 2 (NASA), August 1981) sind von der Sonne Lichtquellen sind, sind beleuchtete Körper. beleuchtete Körper. Ohne Sonne wären sie für uns unsichtbar. 11PS – PHYSIK P. Rendulić 2014 OPTIK 2 1.2 Ausbreitung des Lichts Es soll untersucht werden, wie Licht sich ausbreitet. 1.2.1 Versuch mit durchlöcherter Karton und Nebel Wir stellen einen durchlöcherten Karton über eine eingeschaltete Glühlampe. Dann dunkeln wir den Raum ab und anschließend blasen wir mit einem Nebelgerät in Richtung des Kartons. Feststellung: Von jedem Loch aus kann man Lichtbündel beobachten, welche sich in alle Richtungen des Raums geradlinig fortpflanzen. 1.2.2 Zusammenfassung Von einer Lichtquelle aus breitet sich Licht geradlinig und nach allen Seiten aus. Licht breitet sich geradlinig in alle Richtungen des Raums aus. 1.3 Lichtgeschwindigkeit Die Geschwindigkeit, mit der sich das Licht ausbreitet, wird als Lichtgeschwindigkeit bezeichnet. Die Lichtgeschwindigkeit ist stoffabhängig. Sie ist in materiellen Medien, das heißt in Stoffen, kleiner als im Vakuum (Vakuumlichtgeschwindigkeit c0 = 299 792,458 km/s). Die folgende Tabelle gibt die Lichtgeschwindigkeit in unterschiedlichen Stoffen an: Medium Lichtgeschwindigkeit in km/s Luft 299 705 Wasser 225 000 Ethanol 219 000 Quarzglas 205 500 Plexiglas 201 500 Flintglas 187 500 Diamant 124 000 Zur Vereinfachung der Berechnungen wird die Lichtgeschwindigleit im Vakuum und in Luft oft gleichgesetzt mit 300 000 Kilometern pro Sekunde. Die Lichtgeschwindigkeit im Vakuum und in Luft beträgt c = 300 000 km/s. 11PS – PHYSIK P. Rendulić 2014 OPTIK 3 1.3.1 Beispiel Die Distanz Sonne-Erde beträgt 150 Millionen Kilometer. Wie lange braucht ein Lichtstrahl um von der Sonne zur Erde zu gelangen? Lösung: Für den Zusammenhang zwischen Geschwindigkeit c, zurückgelegter Strecke s und dafür benötigter Zeit t gilt: Geschwindigkeit= Strecke s ⇔ c= Zeit t Eine Formelumstellung gibt: Zeit= Strecke s ⇔ t= Geschwindigkeit c Durch Einsetzen der bekannten Größen finden wir schließlich: s 150 000 000 km 1 500 km 1500 t= = = = s= 500 s= 8,33 min= 8 min20 s c km km 3 300 000 3 s s Ein Lichtstrahl benötigt 8 Minuten und 20 Sekunden, um von der Sonne zur Erde zu gelangen. 1.4 Aufgaben 1.4.1 Lichtstrahl Bestimme die Strecke, welche ein Lichtstrahl in einer Tausendstel Sekunde zurücklegt! 1.4.2 Voyager 1 Das am weitesten von der Erde entfernte und von Menschenhand gebaute Objekt ist die im September 1977 gestartete Raumsonde Voyager 1. Im Jahr 2010 befindet sie sich in einer Entfernung von etwa 17 Milliarden Kilometern. Bestimme die Zeit, die ein von der Sonde abgestrahlter Lichtstrahl brauchen würde, um die Erde zu erreichen! (Graphik: NASA) 1.4.3 Mond Ein Lichtsrahl wird zum Mond geschickt und dort von einem Spiegel reflektiert, welcher den Strahl wieder zur Erde zurückschickt. Der Strahl benötigt für den ganzen Weg 2,6 s. Bestimme die Entfernung Erde-Mond! 11PS – PHYSIK P. Rendulić 2014 OPTIK 4 1.5 Schatten Hinter beleuchtete, lichtundurchlässige Körper kann kein Licht gelangen. Es bilden sich dunkle Gebiete aus, die man als Schatten bezeichnet. 1.5.1 Schattengebiete bei einer punktförmigen Lichtquelle 1.5.2 Schattengebiete bei mehreren Lichtquellen Bei mehreren punktförmigen Lichtquellen oder einer ausgedehnter Lichtquelle (z.B. Leuchtstoffröhre) entstehen unterschiedliche Schatten. Das Gebiet, das vom Licht keiner Lichtquelle erreicht wird nennt man Kernschatten. Die Gebiete, die vom Licht einer punktförmigen Lichtquelle oder Teilen einer ausgedehnten Lichtquelle erreicht werden heißen Halbschatten. 11PS – PHYSIK 2 P. Rendulić 2014 OPTIK 5 REFLEXION DES LICHTS 2.1 Reflexionsgesetz Trifft Licht auf die Oberfläche eines Spiegels (ebene, polierte Oberfläche), so wird es reflektiert (zurückgeworfen). Dafür gilt das Reflexionsgesetz. Wenn Licht an einem Spiegel reflektiert wird, so sind der Einfallswinkel α und der Reflexionswinkel α’ gleich groß: α = α’ Dabei liegen der einfallende Lichtstrahl, das Einfallslot und der reflektierte Lichtstrahl in einer Ebene. 2.1.1 Reguläre und diffuse Reflexion Reguläre Reflexion Diffuse Reflexion Die reguläre Reflexion tritt an glatten Die diffuse Reflexion tritt an rauen Flächen ebenen Oberflächen wie Spiegeln oder auf. Hier wird das Licht in die Wasseroberflächen auf. Das Licht wird unterschiedlichsten Richtungen reflektiert. dabei in eine Richtung reflektiert. 2.2 Aufgaben 2.2.1 Lichtstrahl und Spiegel Ein Lichtstrahl trifft senkrecht auf einen Spiegel. a) Bestimme den Reflexionswinkel und beschreibe, wie das Licht reflektiert wird! b) Um wie viel muss der Spiegel gedreht werden, damit der Strahl um 90° abgelenkt wird? Fertige dazu auch eine Zeichnung an! 2.2.2 Winkelspiegel Zeichne den Verlauf der angegebenen Lichtstrahlen ein! 11PS – PHYSIK 3 P. Rendulić 2014 OPTIK 6 BRECHUNG DES LICHTS Im folgenden Kapitel soll untersucht werden, was man unter der Brechung vom Licht versteht. 3.1 Versuche zur Untersuchung der Brechung 3.1.1 Münze in der Schale Wir legen eine Münze in eine niedrige Schale und blicken so in die Schale, dass die Münze vom Rand der Schale verdeckt ist. Wir können die Münze also nicht sehen. Ohne unseren Blickpunkt zu verändern (wir benutzen eine fest stehende Kamera) gießen wir Wasser in die Schale. Die Münze wird dann sichtbar. Es scheint als würde das von der Münze kommende Licht seine Ausbreitungsrichtung ändern, wenn sich Wasser in der Schale befindet. 3.1.2 Münze im Aquarium Wir legen eine Münze in ein Aquarium (in die Ecke rechts unten), welches zu ¾ mit Wasser gefüllt ist. Wir nehmen dann ein Rohr und versuchen die Münze durch das Rohr zu beobachten, indem wir das Rohr in Bezug zur Wasseroberfläche schief stellen. Sobald wir die Münze sehen können fixieren wir das Rohr an einem Stativ. Dann schieben wir eine Stange durch das Rohr und versuchen die Münze zu berühren. Dies ist jedoch unmöglich. Es scheint als würde das von der Münze kommende Licht sich nicht geradlinig ausbreiten. 3.1.3 Laserstrahl im Aquarium Wir füllen ein Aquarium zu ¾ mit Wasser. Dann schicken wir einen starken Laserstrahl schief auf die Wasseroberfläche. Damit man den Strahl in der Luft sehen kann, benutzen wir ein Nebelgerät. Damit der Strahl im Waser sichtbar ist, geben wir etwas Calciumhydroxid ins Wasser und rühren um. Wir können dann sehr gut erkennen, dass der Lichtstrahl beim Übergang von der Luft ins Wasser, an der Wasseroberfläche, gebrochen wird. Außerdem erkennt man gut, dass ein Teil des Lichts an der Wasseroberfläche reflektiert wird. 11PS – PHYSIK 3.2 P. Rendulić 2014 OPTIK 7 Brechungsgesetz 3.2.1 Brechzahl Um die Brechung des Lichts beschreiben zu können führen wir die Brechzahl (Brechungsindex) ein. Die Brechzahl ist eine optische Materialeigenschaft. Sie ist abhängig vom Medium (=Stoff), in welchem sich das Licht fortpflanzt. Die Brechzahl ist dimensionslos, das heißt sie besitzt keine Einheit. Die Brechzahl n eines Mediums ist definiert als der Quotient aus der Vakuum-Lichtgeschwindigkeit c0 und der Lichtgeschwindigkeit c im Medium: n= c0 c Da die Lichtgeschwindigkeit in materiellen Medien kleiner ist als die VakuumLichtgeschwindigkeit, ist der Brechungsindex n immer größer als 1 (n>1). Beispiele n Luft = 299792 km/s = 1,000292≃ 1,00 299705 km/s n Wasser = 299792 km/s =1,33 225000 km/s Der Brechungsindex hängt ab: • von der Farbe (= Frequenz oder Wellenlänge) des Lichts. Die Brechzahl für violettes Licht ist größer als die für rotes Licht, • von der Temperatur des Mediums (warme Luft hat z.B. eine kleinere Brechzahl als kalte Luft). Medium Farbspektrum Lichtgeschw. In km/s Brechzahl Luft 299 705 1,00 Wasser 225 000 1,33 Ethanol 219 000 1,37 Quarzglas 205 500 1,46 Plexiglas 201 500 1,49 Kronglas 198 500 1,51 Flintglas 187 500 1,60 Diamant 124 000 2,42 3.2.2 Optische Dichte Zwei Medien unterscheiden sich durch ihre optische Dichte. Wenn die Brechzahl vom Medium 1 größer ist als die Brechzahl vom Medium 2 (n 1 > n2), dann sagt man, dass das Medium 1 das optisch dichtere Medium ist. Die Lichtgeschwindigkeit ist dann in diesem Medium geringer als im Medium 2 (c1 < c2). Je kleiner die Brechzahl eines Mediums, ist desto optisch dünner ist dieses Medium. 11PS – PHYSIK P. Rendulić 2014 OPTIK 8 3.2.3 Das Brechungsgesetz Trifft ein Lichtstrahl auf die Trennfläche zwischen zwei Medien, so wird ein Teil des Lichts nach dem Reflexionsgesetz in dem Medium 1 reflektiert und ein Teil dringt in das Medium 2 ein. Der eindringende Lichtstrahl verändert beim Übergang vom Medium 1 ins Medium 2 seine Ausbreitungsrichtung; er wird gebrochen. Dieser Vorgang wird Brechung des Lichts oder Refraktion des Lichts genannt. Der Einfallswinkel α ist der Winkel zwischen Lot und einfallendem Lichtstrahl. Als Brechungswinkel β bezeichnet man den Winkel zwischen Lot und gebrochenem Lichtstrahl. Das Lot steht senkrecht zur Grenzfläche. 3.2.4 Experimentelle Herleitung des Brechungsgesetzes Beim Übergang Luft → Plexiglas wird für unterschiedliche Einfallswinkel der dazugehörige Brechungswinkel gemessen. Die Messwerte werden in eine Tabelle eingetragen. Zur Auswertung werden die Größen sin α und sin β sowie deren Quotient berechnet. α in ° β in ° sin α sin β sin α / sin β 0 0 0,000 0,000 - 20 13 0,342 0,225 1,52 40 26 0,643 0,438 1,47 60 36 0,866 0,588 1,47 70 40 0,940 0,643 1,46 80 42 0,985 0,669 1,47 85 43 0,996 0,682 1,46 90 - 1,000 - - Die Tabelle zeigt, dass der Quotient sin α / sin β konstant ist. Die Größen sin α und sin β sind daher proportional zueinander. Desweiteren kann man feststellen, dass sin α n2 = sin β n1 denn n2 n Plexiglas 1,49 = = = 1,49 n1 n Luft 1,00 11PS – PHYSIK P. Rendulić 2014 OPTIK 9 3.2.5 Formulierung des Brechungsgesetzes sin α n2 = sin β n1 • α: Einfallswinkel im Medium 1 • β: Einfallswinkel im Medium 2 oder • n1: Brechungszahl vom Medium 1 n 1⋅ sin α= n2⋅ sin β • n2: Brechungszahl vom Medium 2 (Brechungsgesetz nach Snellius) 3.2.6 Brechungsgesetz: Analyse Je nachdem ob ein Lichtstrahl vom optisch dünneren in das optisch dichtere Medium übergeht oder umgekehrt, unterscheidet man die folgenden 2 Fälle: Übergang vom optisch dünneren in das optisch Übergang vom optisch dichteren in das optisch dichtere Medium (z.B von Luft nach Wasser) dünnere Medium (z.B von Wasser nach Luft) n1 < n 2 → α > β n1 > n 2 → α < β Der Einfallswinkel ist größer als der Der Brechungswinkel ist größer als der Brechungswinkel. Der Strahl wird zum Lot Einfallswinkel. Der Strahl wird vom Lot weg hin gebrochen. gebrochen. Ein Strahl der senkrecht auf die Grenzfläche auftrifft wird nicht gebrochen. 11PS – PHYSIK 3.3 P. Rendulić 2014 OPTIK 10 Totalreflexion Beim Übergang vom optisch dichteren (hier Wasser) in das optisch dünnere Medium (hier Luft) wird der Strahl vom Lot weg gebrochen. Bei α = 90° erreicht der Brechungswinkel seinen Maximalwert und der austretende Strahl läuft tangential zur Grenzfläche. Der zugehörige Einfallswinkel heißt Grenzwinkel βG. Wird er überschritten, so beobachtet man eine vollständige Reflexion des Lichtstrahls, die den Namen Totalreflexion trägt. Lampe unter Wasser In diesem Fall kann der einfallende Lichtstrahl nicht aus dem optisch dichteren in das optisch dünnere Medium austreten. In diesem Fall gilt das Reflexionsgesetz: β = β' 3.3.1 Bestimmung des Grenzwinkels Für den Grenzfall hat der Brechungswinkel einen Wert von α = 90° (im dünneren Medium). In diesem Fall entspricht der Einfallswinkel β (im dichteren Medium) dem Grenzwinkel βG (β = βG). Das Brechungsgesetz kann folgendermaßen angeschrieben werden: n 2⋅ sin G = n 1⋅ sin 90 ° ⇔ 1 ⇔ sinβG = n1 n2 Der Grenzwinkel, ab dem beim Übergang vom optisch dichteren in das optisch dünnere Medium Totalreflexion eintritt, wird daher nach der folgenden Formel berechnet: βG= arcsin ( Es gilt z.B Luft, n1 <1 n2 n2 denn n 1< n 2 ( n1 n1 ) n2 ist die Brechzahl des optisch dünneren Mediums, ist die Brechzahl des optisch dichteren Mediums z.B. Wasser). 3.3.2 Beispiel: Übergang Wasser → Luft Grenzwinkel für den Übergang Wasser → Luft: βG= arcsin ( nLuft 1 )= arcsin ( )= 48,8 ° nWasser 1,33 11PS – PHYSIK P. Rendulić 2014 OPTIK 11 3.3.3 Technische Anwendung: das Glasfaserkabel Die Totalreflexion von Licht wird bei Glasfaserkabeln genutzt, die zur optischen Informationsübertragung eingesetzt werden. Glasfaserkabel bestehen aus einem Kern aus klarem Glas oder Kunststoff, der von einem Mantel aus einem optisch dünneren Medium umgeben ist. Dadurch wird erreicht, dass das Licht an den Rändern total reflektiert wird und somit in der Glasfaser verbleibt und weitergeleitet wird. In der Medizin werden biegsame Glasfaserkabel in Endoskopen verwendet, um Licht ins Körperinnere und umgekehrt Bilder aus dem Körper nach außen zu befördern 3.4 Das Prisma Prismen sind Körper aus lichtdurchlässigen Stoffen, die von zwei sich schneidenden Ebenen begrenzt sind. Die Schnittkante dieser beiden Ebenen wird Brechungskante oder brechende Kante genannt. Der Winkel γ an der brechenden Kante wird brechender Winkel oder Prismenwinkel genannt. 3.4.1 Strahlengang beim Prisma Trifft ein monochromatischer Lichtstrahl auf eine Seite eines Prismas, so wird er im Regelfall zweimal gebrochen und tritt somit auf der zweiten Seite in eine neue Richtung aus. Insgesamt wird das Licht durch die zweimalige Brechung stärker abgelenkt als bei einmaliger Brechung. Der Winkel zwischen den Richtungen des einfallenden Lichtstrahles und des austretenden Lichtstrahles wird Ablenkungswinkel genannt. Monochromatisches Licht ist Licht einer einzigen Wellenlänge, das heißt Licht einer einzigen Farbe (siehe auch → Zugehörigkeit von Farbe und Wellenlänge). 11PS – PHYSIK P. Rendulić 2014 OPTIK 12 3.4.2 Farbzerlegung des Lichts Die Abbildung zeigt, dass weißes Licht beim Durchgang durch das Prisma aufgefächert und dabei in farbige Bestandteile zerlegt wird. Weißes Licht ist aus farbigen Anteilen zusammengesetzt. Diese Anteile können mithilfe eines Prismas voneinander getrennt werden. Das entstehende Farbband heißt Spektrum Die Zerlegung des Lichts am Prisma kommt dadurch zustande, dass violettes Licht stärker gebrochen wird als rotes das heißt, dass die Brechzahl für violettes Licht größer ist als für rotes Licht. Ursache dafür ist, dass die Lichtgeschwindigkeit, und somit auch die Brechzahl von der Farbe abhängt. 3.4.3 Wellenlängen Die folgende Tabelle zeigt dir Zugehörigkeit von Farbe und Wellenlänge Infrarot Rot Orange Gelb Grün Blau Violett Ultraviolett 0,75-100 μm 650-750 nm 585-650 nm 575-585 nm 490-575 nm 420-490 nm 400-420 nm 15-400 nm 3.4.4 Lichtgeschwindigkeit in km/s für verschiedene Farben Die folgende Tabelle zeigt die Lichtegeschwindigkeit in km/s für Kronglas und Wasser in Abhängigkeit der Farbe Medium Kronglas Wasser Rot 198 407 225 408 Orange 198 014 225 069 Gelb 197 883 224 901 Grün 197 362 224 564 Blau 197 102 224 228 Violett 196 328 223 559 11PS – PHYSIK P. Rendulić 2014 OPTIK 13 3.4.5 Anwendung für Prismen Umlenkprismen Prismen, bei denen das Licht in eine andere Richtung gelenkt wird, nennt man Umlenkprismen. Durch zweifache Brechung erfolgt eine Umlenkung des Lichts. Durch Totalreflexion wird das Licht um 90° umgelenkt. Umkehrprismen Prismen, bei denen die Lage von einfallenden und reflektierten Strahlen gerade umgekehrt wird, nennt man Umkehrprismen. Durch zweifache Totalreflexion erfolgt eine Umkehrung des Lichts. 3.5 Durch zweifache Brechung und Totalreflexion erfolgt eine Umkehrung des Lichts. Aufgaben 3.5.1 Unterschiedliche Medien Erkläre, wie das Licht in den folgenden Fällen gebrochen wird! Erkläre dabei, ob die Brechung zum Lot hin oder vom Lot weg erfolgt! 11PS – PHYSIK P. Rendulić 2014 OPTIK 14 3.5.2 Prisma Ein Lichtstrahl trifft von Luft kommend auf ein gleichseitiges Prisma aus Flintglas (siehe Figur). Berechne die Ablenkungen an beiden Grenzflächen! Wie groß ist die Gesamtablenkung? 3.5.3 Planparallele Platte Ein Lichtstrahl trifft aus Luft kommend unter einem Winkel von 60° auf eine planparallelle Platte aus Plexiglas. Zeichne den Strahlenverlauf und kontrolliere dein Resultat durch einen Versuch! 3.5.4 Aquarium Ein Lichtstrahl trifft unter einem Winkel von 70° auf ein mit Wasser gefülltes Aquarium, auf dessen Boden ein Spiegel liegt. Das Wasser ist 15 cm tief. Zeichne den Verlauf des Lichtstrahls ein! Bestimme den Gesamtablenkungswinkel des Lichtstrahls! Darunter versteht man den Winkel unter der Richtung des einfallenden Lichtstrahls und der Richtung des aus dem Wasser austretenden Lichtstrahls. Bestimme den Abstand zwischen den beiden Punkten, in welchen der einfallende und der reflektierte Lichtstrahl durch die Wasseroberfläche stoßen! 3.5.5 Grenzwinkel Berechne den Grenzwinkel der Totalreflexion für den Übergang von Flintglas nach Luft! 3.5.6 Totalreflexion im Glasfaserkabel * Welche Brechzahl muss ein zylindrisches, von Luft umgebenes Glasfaserkabel mindestens haben, damit alle durch seine Stirnfläche eintretenden Strahlen durch Totalreflexion weitergeleitet werden? 11PS – PHYSIK 4 P. Rendulić 2014 OPTIK 15 Optische Linsen 4.1 Linsenarten Eine Linse ist ein rotationssymmetrischer Körper der meist aus Glas oder transparentem Kunststoff hergestellt ist. Die Linse ist von zwei Kugelflächen begrenzt (Kugelflächen sind leicht und kostengünstig herzustellen, man spricht von sphärischen Linsen). Man unterscheidet Sammellinsen (oder Konvexlinsen) und Zerstreuungslinsen (oder Konkavlinsen). Sammellinsen sind in der Mitte dicker als am Rand. Zerstreuungslinsen sind in der Mitte dünner als am Rand. Als optische Achse bezeichnet man die Gerade die senkrecht zur Symmetrieachse der Linse steht und durch deren Mittelpunkt geht. 4.2 Brechung bei der Sammellinse Die nebenstehende Figur zeigt das Modell einer Sammellinse. Dabei sind die gewölbten Kugelflächen zur Veranschaulichung durch einzelne Prismen dargestellt. Die Prismen sind so geformt, dass alle Strahlen die parallel zur optischen Achse verlaufen sich in einem gemeinsamen Punkt, dem Brennpunkt, kreuzen. Strahlen die nahe an der optischen Achse verlaufen müssen nur geringfügig abgelenkt werden. Sie treffen daher nahezu senkrecht auf die Prismenfläche auf. Strahlen die weiter entfernt von der optischen Achse verlaufen müssen weiter abgelenkt werden, um durch den Brennpunkt zu verlaufen. Für diese Strahlen muss daher der Einfallswinkel an der Grenzfläche größer sein. Die Neigung der Prismenfläche ist dementsprechend angepasst. Im Fall einer reellen (dünnen) Linse erlaubt die Kugelwölbung, dass Strahlen, die parallel zur optischen Achse verlaufen, sich in guter Näherung alle im Brennpunkt kreuzen. 11PS – PHYSIK P. Rendulić 2014 OPTIK 16 4.3 Brennweite und Brechkraft Die Distanz zwischen Brennpunkt und Linsenmitte wird Brennweite f genannt. Oft wird anstatt der Brennweite die Brechkraft D in Dioptrien (dpt) angegeben. Sie ist definiert als: D= 1 f Eine Linse von 1 m Brennweite hat daher eine Brechkraft von 1 dpt. Für die Zerstreuungslinse sind die Brennweite und die Brechkraft negativ. 4.4 Strahlengang in dünnen Linsen Zur Bildkonstruktion werden die sogenannten Hauptstrahlen benutzt. Dabei handelt es sich um Strahlen deren Ablenkung durch die Linse ohne Berechnung bekannt ist. 4.4.1 Sammellinse ► Ein Lichtstrahl, welcher parallel zur optischen Achse verläuft, verläuft nach der Brechung durch den Brennpunkt F’. ► Ein Lichtstrahl, welcher durch den Brennpunkt F verläuft, verläuft nach der Brechung parallel zur optischen Achse weiter. ► Ein Lichtstrahl, welcher durch den Mittelpunkt O verläuft, verläuft in gerader Linie weiter und wird nicht gebrochen. 4.4.2 Zerstreuungslinse ► Ein Lichtstrahl, welcher parallel zur optischen Achse verläuft, scheint nach der Brechung aus dem Brennpunkt F zu kommen. ► Ein Lichtstrahl, welcher durch den Brennpunkt F’ verlaufen müsste, verläuft nach der Brechung parallel zur optischen Achse weiter. ► Ein Lichtstrahl, welcher durch den Mittelpunkt O verläuft, verläuft in gerader Linie weiter und wird nicht gebrochen. 4.5 Bilder durch Sammellinsen 4.5.1 Versuch Wir dunkeln den Raum ab, und stellen eine Kerze auf den Experimentiertisch. Zwischen die Kerze und eine weiße Wand stellen wir eine Sammellinse. Wir beobachten dabei, dass 2 Positionen der Linse existieren, welche es ermöglichen ein scharfes Bild auf der Wand zu erzeugen. Wenn die Linse nahe bei der Kerze steht entsteht ein vergrößertes Bild, wenn sie jedoch nahe an der Wand steht entsteht ein verkleinertes Bild. 11PS – PHYSIK P. Rendulić 2014 OPTIK 17 4.5.2 Grundlagen Im Idealfall wird Licht, das von einem Punkt ausgeht, durch eine Sammellinse so gebrochen, dass es wieder in einem Punkt vereinigt wird. Bilder an Sammellinsen lassen sich einfach konstruieren, wenn die Hauptstrahlen benutzt werden. Die Figur zeigt zeigt die Größen die bei der Bildentstehung eine Rolle spielen. Es handelt sich um: F, F’ Brennpunkte der Linse f Brennweite der Linse G Gegenstandsgröße (Größe des Gegenstandes) B Bildgröße (Größe des Bildes) g Gegenstandsweite (Entfernung zwischen Gegenstand und Linsenmitte) b Bildweite (Entfernung zwischen Bild und Linsenmitte) 4.5.3 Reelle und virtuelle Bilder Ob reelle oder virtuelle Bilder entstehen, hängt von der Position des Gegenstandes zur Linse ab. ► Bei einem reellen Bild konvergieren (vereinigen sich) die Strahlen hinter der Linse, somit können diese Bilder auf einem Schirm aufgefangen werden. Reelle Bilder entstehen, wenn die Gegenstandsweite größer als die Brennweite ist. 11PS – PHYSIK P. Rendulić 2014 OPTIK 18 ► Bei einem virtuellen Bild divergieren die Strahlen hinter der Linse (ihre gedachte Verlängerungen vereinigen sich jedoch), somit können diese Bilder durch unser Auge erkannt werden, jedoch nicht auf einem Schirm sichtbar gemacht werden. In diesem Fall funktioniert die Sammellinse als Lupe Virtuelle Bilder entstehen, wenn die Gegenstandsweite kleiner als die Brennweite ist. 4.6 Bildeigenschaften Die folgende Tabelle fasst die Bildweite und die Bildeigenschaften in Abhängigkeit von der Gegenstandsweite zusammen. Gegenstandsweite g Bildweite b Bildeigenschaften ∞ f verkleinert, umgekehrt, reell 2f g∞ f b2f verkleinert, umgekehrt, reell 2f 2f gleich groß, umgekehrt, reell f g 2f 2f b∞ vergrößert, umgekehrt, reell f ∞ sehr groß, umgekehrt, reell g f − ∞ b0 vergrößert, aufrecht, virtuell g 0 b 0 gleich groß, aufrecht, virtuell 11PS – PHYSIK 4.7 P. Rendulić 2014 OPTIK 19 Technische Anwendung: die einäugige Spiegelreflexkamera Bei einer Spiegelreflexkamera gelangt das Licht durch die Linsen des Objektivs (1) und wird dann vom Schwingspiegel (2) reflektiert und auf die Einstellscheibe (5) projiziert. Mit einer Sammellinse (6) und durch die Totalreflexion innerhalb des Pentaprismas (7) wird das Bild schließlich im Sucher (8) sichtbar. Während einer Aufnahme klappt der Spiegel nach oben (im Bild durch einen Pfeil gekennzeichnet), und der Verschluss (3) öffnet sich; das Bild wird dann nicht mehr in das Pentaprisma umgelenkt, sondern gelangt auf die Filmebene (4) und belichtet den Film. Um das Bild scharf zu stellen wird die Distanz zwischen Linsensystem (welches wie eine Sammellinse wirkt) und Film verändert. Bei weit entfernten Gegenständen steht das Linsensystem näher an der Filmebene als bei nahen Gegenständen. 4.8 Abbildungsmaßstab und Abbildungsgesetz Die Zusammenhänge zwischen der Gegenstandsgröße G, der Bildgröße B, der Gegenstandsweite g, der Bildweite b und der Brennweite f der Linse können mithilfe von zwei Gesetzen beschrieben werden: dem Abbildungsmaßstab und dem Abbildungsgesetz. 4.8.1 Abbildungsmaßstab Aus der Ähnlichkeit der gefärbten Dreiecke folgt 11PS – PHYSIK P. Rendulić 2014 OPTIK 20 B G = b g und durch Umstellen B b = =Γ G g Γ bezeichnet den Abbildungsmaßstab. Er gibt an, wie viel mal das Bild größer ist, als der Gegenstand. 4.8.2 Abbildungsgesetz Aus der Ähnlichkeit der gefärbten Dreiecke folgt G B = g− f f B f ⇔ = G g− f Unter Berücksichtigung des Abbildungsmaßstabs ergibt sich mit B b = G g b f = g g− f ⇔ g⋅ f = b⋅ g− f ⇔ g⋅ f = b⋅ g− b⋅ f ⇔ g⋅ f b⋅ f = b⋅ g ⇔ f⋅ gb = b⋅ g b⋅ g ⇔ f= gb 1 g b ⇔ = f b⋅ g 1 1 1 ⇔ = f b g Daher das Abbildungsgesetz: 1 1 1 = f b g Das Abbildungsgesetz gilt sowohl für Sammellinsen als auch für Zerstreuungslinsen. Für die unterschiedlichen Größen müssen folgende Vorzeichen gewählt werden: 11PS – PHYSIK P. Rendulić 2014 Brennweite f OPTIK Sammellinse f 0 Zerstreuungslinse* f 0 g 0 und G0 Gegenstandsgröße g virtueller Gegenstand* g 0 und G0 Bildweite b relles Bild b0 und B0 Bildgröße B virtuelles Bild b0 und B0 Gegenstandsweite g reller Gegenstand 21 4.8.3 Experimentelle Überprüfung des Abbildungsmaßstabes und des Abblidungsgesetzes Für unterschiedliche Linsen und Anordnungen wird von einem Gegenstand (z.B. Diapositiv) ein Bild auf einem Schirm erzeugt. Die relevantent Größen werden gemessen und die Messwerte werden in die folgende Tabelle eingetragen: f (cm) Man G (cm) kann g (cm) feststellen, B (cm) dass b (cm) sowohl der B/G b/g 1/f 1/b+1/g Abbildungsmaßstab als auch B b 1 1 1 = = . Abbildungsgleichung gültig sind, denn in allen Fällen gilt und G g f b g die 11PS – PHYSIK P. Rendulić 2014 OPTIK 22 4.9 Das menschliche Auge Das menschliche Auge ist ein kompliziertes Organ, bestehend aus Muskeln, Fasern, Häuten, Blutgefäßen und Nerven. Es erlaubt uns zu Sehen, indem es die wichtigsten optischen Bauelemente enthält um Bilder von Gegenständen zu erzeugen: • ein Linsensystem bestehend aus Augenlinse und Glaskörper, welches wie eine Sammellinse wirkt (Brennweite von ca. 23 mm), • die Netzhaut als Schirm, diese besteht aus zwei Arten von lichtempfindlichen Zellen, den helldunkelempfindlichen Stäbchen und den farbempfindlichen Zäpfchen. Wenn Licht durch die Pupille ins Auge fällt, dann wird es so gebrochen, dass auf der Netzhaut ein verkleinertes, reelles, umgekehrtes und seitenvertauschtes Bild entsteht. Über den Sehnerv gelangen die Bildinformationen zur weiteren Verarbeitung ins Gehirn. 4.9.1 Funktionsweise der Augenlinse Damit wir scharf sehen, muss das Auge sich an unterschiedliche Bedingungen anpassen können. Da Gegenstände unterschiedlich weit von uns entfernt sein können, kann das Auge durch ein Muskelsystem die Krümmung der Augenlinse und damit die Brennweite stufenlos verändern. Diesen Vorgang nennt man Akkomodation. Er passiert unwillkürlich. Beim scharfen Sehen von weit entfernten Gegenständen ist die Linse abgeflacht und nur wenig gekrümmt (große Brennweite). Beim Scharfen Sehen von nahen Gegenständen ist die Linse stärker gewölbt, was zu einer stärkeren Brechung des Lichts und zu einer kleineren Brennweite führt. 11PS – PHYSIK P. Rendulić 2014 OPTIK 23 4.10 Sehfehler und Korrekturmöglichkeiten Bei vielen Menschen ist die Anpassung des Auges an unterschiedlich entfernte Gegenstände gestört. Diese Sehfehler sind teilweise angeboren (oft die Kurzsichtigkeit), sie können aber auch im forstreitenden Alter auftreten (oft die Weitsichtigkeit). Kurzsichtigkeit Weitsichtigkeit Bei kurzsichtigen Menschen ist der Augapfel zu lang. Dadurch entsteht das scharfe Bild von weit entfernten Gegenständen vor der Netzhaut. Für den Kurzsichtigen bedeutet das, dass das wahrgenommene Bild verschwommen ist. Bei weitsichtigen Menschen ist der Augapfel zu kurz. Dadurch entsteht das scharfe Bild von nahen Gegenständen hinter der Netzhaut. Für den Weitsichtigen bedeutet das, dass das wahrgenommene Bild verschwommen ist. Kurzsichtige können nur sehr nahe Gegenstände Weitsichtige können nur weit entfernte Gegenstände scharf sehen. scharf sehen. Zur Korrektur der Kurzsichtigkeit benutzt man eine Zur Korrektur der Weitsichtigkeit benutzt man eine Brille, deren Gläser Sammellinsen sind. Brille, deren Gläser Zerstreuungslinsen sind. Dadurch erreicht man, das das von weit entfernten Gegenständen auf das Auge treffende Licht, so zerstreut wird, dass das scharfe Bild weiter hinten, auf der Netzhaut entsteht. Dadurch erreicht man, das das von bahen Gegenständen auf das Auge treffende Licht, so gebündelt wird, dass das scharfe Bild weiter vorne, auf der Netzhaut entsteht. Sehfehler kann man auch durch Kontaktlinsen und teilweise durch Operationen am Auge korrigieren. Die Altersweitsichtigkeit kommt dadurch zustande, dass die Augenlinse im fortschreitenenden Alter an Elastizität verliert, dadurch nicht mehr so stark verformt werden kann und somit die Akkomodation an nahe Gegenstände nicht mehr möglich ist. Auch diese Form der Weitsichtigkeit wird durch eine Brille mit Sammellinsen korrigiert. 4.10.1 Lupe Sinn einer Lupe ist, kleine Gegenstände vergrößert zu sehen. Damit dies möglich ist, muss sich der Gegenstand innerhalb der Brennweite der Sammellinse befinden. Es entsteht ein vergrößertes, aufrechtes, seitenrichtiges und virtuelles Bild, das mit dem Auge betrachtet wird. Zum Beschreiben einer Lupe benutzt man die Normalvergrößerung. Man erhält sie, wenn sich der Gegenstand nahe am Brennpunkt der Sammellinse befindet und sich die Augen in der deutlichen Sehweite von 25 cm vor der Lupe befinden. Mit der Lupe sind 10 bis 20-fache Vergrößerungen möglich. 25 cm , wobei f der f Brennweite der Lupe entspricht. Für die Vergrößerung einer Lupe gilt: V= 11PS – PHYSIK 4.10.2 P. Rendulić 2014 OPTIK 24 Mikroskop Wenn man stärkere Vergrößerungen als mit einer Lupe möglich erreichen, so muss man ein Mikroskop benutzen. Das Mikroskop besteht vereinfacht gesehen aus 2 Sammellinsen (oder Gruppen von Linsen), dem Objektiv und dem Okular. Der Gegenstand befindet sich zwischen der einfachen und der doppelten Brennweite des Objektivs. Dadurch entsteht im Tubus des Mikroskops ein vergrößertes und reelles Bild des Gegenstands. Dieses Zwischenbild befindet sich innerhalb der Brennweite des Okulars. Dadurch wirkt das Okular als Lupe, wodurch man mit dem Auge ein stark vergrößertes, umgekehrte, seitenvertauschtes virtuelles Bild des Gegenstands sehen kann. Mit dem Objektiv sind Vergrößerungen möglich. bis zu 1000-fache t⋅ s f Obj⋅ f Ok wobei t der Tubuslänge und s der deutlichen Sehweite entspricht. Für die Vergrößerung eines Mikroskops gilt: V = V Objektiv⋅ V Okular = 4.11 Aufgaben Für jede Aufgabe soll ein geeignetes Schema / Skizze angefertigt werden. 4.11.1 Sammellinse und Feuer Erkläre, wie du mit einer Sammellinse (z.B. einer Vergrößerungslupe) und Sonnenlicht ein Feuer entzünden kannst! Fertige dazu auch eine entsprechende Zeichnung an! 4.11.2 Linse In welcher Entfernung von einer Sammellinse (Brennweite: 3 cm) wird ein Gegenstand scharf abgebildet, wenn dieser sich 9 cm vor der Linse befindet? 11PS – PHYSIK P. Rendulić 2014 OPTIK 25 4.11.3 Fotoapparat Mit einer Kleinbildkamera der Brennweite 50 mm soll eine Person von 1,80 Meter Größe im Hochformat formatfüllend fotografiert werden. Bei Hochformat beträgt die maximale Bildgröße 36 mm. Wie groß muss die Gegenstandsentfernung sein? 4.11.4 Abbildung vom Mond Mit der gleichen Kleinbildkamera wie in dervorherigen Aufgabe solll der Mond (G = 3476 km, g = 384400 km) abgebildet werden. Berechne die Bildgröße! Wie groß wäre die Abbildung des Mondes, wenn man als Objektiv ein Teleskop mit einer Brennweite von 1 500 mm nehmen würde? 4.11.5 Bildkonstruktion Konstruiere für die folgenden Fälle das Bild! Erkläre auch, ob es sich um ein reelles oder ein virtuelles Bild handelt! 11PS – PHYSIK P. Rendulić 2014 OPTIK 26 4.11.6 Bildkonstruktion Konstruiere die Bilder für die folgenden Fälle: Berechne auch jeweils die Bildweite, sowie die Bildgröße! 4.11.7 Bildkonstruktion Mit einer Sammellinse von 6 cm Brennweite soll ein 3 cm großen Gegenstandes, welcher 12 cm von der Linse entfernt steht, abgebildet werden. Fertige die Bildkonstruktion an und bestimme die Bildweite und die Bildgröße. 4.11.8 Sammellinse und Feuer Erkläre, wie du mit einer Sammellinse (z.B. einer Vergrößerungslupe) und Sonnenlicht ein Feuer entzünden kannst! Fertige dazu auch eine entsprechende Zeichnung an! 4.11.9 Lupe Eine Sammellinse (f = 5 cm) soll als Lupe zur Betrachtung eines 4,9 cm entfernten Objektes der Größe 1 mm benutzt werden. Wo entsteht das Bild und wie groß ist es? 4.11.10 Welche Linse? Bestimme für die folgenden 2 Fälle die Position, sowie die Brechkraft der Sammellinse! 11PS – PHYSIK 5 P. Rendulić 2014 OPTIK 27 Dispersion von Licht 5.1 Das Prisma Prismen sind Körper aus lichtdurchlässigen Stoffen, die von zwei sich schneidenden Ebenen begrenzt sind. Die Schnittkante dieser beiden Ebenen wird Brechungskante genannt. Der Winkel γ an der brechenden Kante wird Prismenwinkel genannt. 5.1.1 Strahlengang beim Prisma Trifft ein einfarbiger Lichtstrahl auf eine Seite eines Prismas, so wird er im Regelfall zweimal gebrochen und tritt somit auf der zweiten Seite in eine neue Richtung aus. Insgesamt wird das Licht durch die zweimalige Brechung stärker abgelenkt als bei einmaliger Brechung. Der Winkel zwischen den Richtungen des einfallenden Lichtstrahles und des austretenden Lichtstrahles wird Ablenkungswinkel δ genannt. 5.1.2 Farbzerlegung des Lichts Weißes Licht wird beim Durchgang durch das Prisma aufgefächert und dabei in farbige Bestandteile zerlegt. Das entstehende Farbband heißt Spektrum. Die Zerlegung des Lichts am Prisma kommt dadurch zustande, dass violettes Licht stärker gebrochen wird als rotes Licht. Das Phänomen der Lichtzerlegung in Farben nennt man Dispersion. Farbspektrum von weißem Licht: 11PS – PHYSIK 5.2 P. Rendulić 2014 OPTIK 28 Der Regenbogen Einen Regenbogen kann man dann sehen, • wenn es regnet, • man die Sonne im Rücken hat • und Sonnenlicht auf die Wassertropfen trifft, die sich noch in der Luft befinden. Die Farbfolge beim Regenbogen ist immer die gleicher und erinnert an das Farbspektrum, das wir bei der Dispersion am Prisma gesehen haben. Die Ursache für die Entstehung der Farben des Regenbogens ist auch hier hauptsächlich die Dispersion des Lichts durch Brechung (es treten auch noch Interferenzeffekte auf, auf die wir hier nicht weiter eingehen). 5.2.1 Entstehung des Regenbogens • Trifft weisses Licht auf einen kugelförmigen Regentropfen, so wird es beim Übergang Luft -Wasser gebrochen, dann teilweise reflektiert und beim Übergang Wasser-Luft wieder gebrochen. Während dieser Vorgänge wird das Licht wie beim Prisma durch Dispersion in die einzelnen Spektral-Farben zerlegt. Die Summe aller Eindrücke des von vielen Regentropfen umgelenkten Lichts ergibt den Regenbogen. 5.3 • Untersuchungen zeigen, dass man den Regenbogen immer unter einem Winkel von 42° in Bezug zur Einfallsrichtung des Sonnenlichts sieht.Ein Nebenregenbogen erscheint in einem Winkel von 52° zum Sonnenlicht. • Beim Nebenregenbogen ist die Farbfolge umgekehrt und der Farbeindruck weniger ausgeprägt. Der Nebenregenbogen ensteht durch zweifache Brechung und zweifache Reflexion des Lichts. Aufgaben 5.3.1 Künstlicher Regenbogen Überlege eine Versuchsanordnung, mit der du einen Regenbogen erzeugen kannst. Beschreibe deine Planung genau und begründe wichtige Schritte. 5.3.2 Regenbogen und Schatz Nimm zur Aussage „ Am Ende eines Regenbogens ist ein Schatz verborgen“ Stellung! Kann man das Ende eines Regenbogens überhaupt erreichen? Begründe deine Antwort! 11PS – PHYSIK 5.4 P. Rendulić 2014 OPTIK 29 Spektrale Zerlegung des Lichts Zerlegt man das Licht einer Glühlampe oder das Sonnenlicht mit der Hilfe eines Prismas, so entsteht auf einem Schirm ein lückenloses Farbband, ein kontinuierliches Spektrum. (siehe Figur) Glühende feste Körper und Gase unter hohem Druck senden Licht mit einem kontinuierlichen Spektrum aus. Wenn man einen Magnesiastab, den man zuvor in eine Salzläsung getaucht hat, in eine Bunsenbrennerflamme hält, so stellt man fest, dass diese je nach Salz unterschiedlich farbig aufleuchtet. Auch Gase unter niedrigem Druck können in speziellen Lampen zum Leuchten angeregt werden (z.B bei Leuchtreklamen: Neon → orange). Flammenfärbung und leuchtende Gase Natrium färbt eine Flamme gelb. Lithium färbt eine Flamme rot. Leuchtreklame Erzeugt man mithilfe eines Prismas ein Spektrum dieser leuchtenden Gase, so stellt man fest, dass es sich um ein diskontinuierliches Linienspektrum handelt. Das Linienspektrum ist charakteristisch für das Gas, aus dem es entsteht. Gase unter niedrigem Druck senden farbiges Licht aus. Bei der Zerlegung dieses Lichts entsteht ein Linienspektrum, Linienspektren unterschiedlicher Gase Wasserstoff Helium Neon Natrium Quecksilber 11PS – PHYSIK P. Rendulić 2014 OPTIK 30 5.4.1 Spektralanalyse Wenn man die Spektren vieler Stoffe kennt, kann man die Zusammensetzung eines unbekannten Stoffgemisches durch eine Spektralanalyse bestimmen. Um eine Stoffprobe zu analysieren (Chemie, Medizin) wird diese zum Leuchten angeregt und in einem Spektrometer spektral zerlegt. Durch den Vergleich des ermittelten Spektrums mit Spektraltafeln, auf denen die Spektrallinien unterschiedlicher Elemente verzeichnet sind, lassen sich die Bestandteile der Probe ermitteln. Die Spektralanalyse wird aber auch in der Astrophysik eingesetzt. So kann z.B. mit der Hilfe von Spektren die Zusammensetzung von Sternen bestimmt werden. 5.5 Infrarot und Ultraviolett 5.5.1 Infrarote Strahlung, IR-Strahlung In der Nähe eines Heizkörpers oder einer Herdplatte spürt man Wärmestrahlung. Auch in der Nähe einer Glühlampe oder im Sonnenlicht bemerkt man, dass Wärme abgestrahlt wird. Diese Wärmestrahlung heißt Infrarotstrahlung. VERSUCH: Mit einer leistungsstarken Halogenlampe und einem Prisma wird ein breites Spektrum auf einem Schirm erzeugt. Mit einer Thermosäule wird das gesamte Spektrum langsam abgetastet. Dabei stellt man fest, dass der Zeigerausschlag jenseits von Rot am größten ist. 5.5.2 Ultraviolette Strahlung, UV-Strahlung Das Licht der Sonne wärmt uns nicht nur, es kann uns auch bräunen oder einen schmerzvollen Sonnenbrand verursachen. Hierfür ist der energiereiche ultraviolette Bestandteil des Sonnenlichts verantwortlich. VERSUCH: Das Licht einer Quecksilberdampflampe wird mit einem Prisma in ein Spektrum zerlegt. Der obere Teil des Schirms ist mit Zinksulfid beschichtet. Auf dieser Schicht sind jenseits von Violett deutlich helle Linien zu erkennen. Der Zinksulfid-Schicht strahlt sichtbares Licht aus, wenn sie von ultravioletter Strahlung getroffen wird. 5.5.3 Zusammenfassung Im Spektrum der Sonne und anderer Lichtquellen gibt es jenseits von Rot die Infrarotstrahlung und jenseits des Violett die ultraviolette Strahlung. Beide Strahlungsarten sind für das menschliche Auge unsichtbar. 11PS – PHYSIK P. Rendulić 2014 OPTIK 31 5.5.4 Anwendungen in Natur und Technik Infrarotfernbedienung IR-Fernbedienungen senden ein Signal im unsichtbaren Infrarotbereich aus. Als Strahlungsquelle dienen meistens Leuchtdioden. Das Signal wird mit einer Frequenz von 38 kHz ausund eingeschaltet. Durch Modulation dieses Sendesignals werden Informationen zum Empfänger übertragen. UV-Strahlung und Ozon-Schicht In einer Höhe von etwa 20 bis 40 km bildet sich aus Luftsauerstoff (O2) unter Einfluss der im Sonnenlicht enthaltenen UV-Strahlung Ozon (O3). Diese Schicht absorbiert daher einen Teil der im Sonnenlicht enthaltenen UV-Strahlung, welche für Lebewesen gefährlich ist. 5.6 Aufgaben 5.6.1 Schutz vor UV-Strahlung Wie kannst du dich vor UV-Strahlung schützen? 5.6.2 Ozon-Loch Was versteht man unter dem Ozon-Loch? Wie ist es entstanden? Was ist gefährlich daran? Wie kann man es „reparieren“. 11PS – PHYSIK 5.7 P. Rendulić 2014 OPTIK 32 Elektromagnetisches Spektrum * Licht ist eine elektromagnetische Welle. Als elektromagnetische Welle bezeichnet man eine Welle aus gekoppelten elektrischen und magnetischen Feldern. Zu ihnen gehören unter anderem Radiowellen, Mikrowellen, Infrarotstrahlung, sichtbares Licht, UV-Strahlung sowie Röntgen- und Gammastrahlung. Der einzige Unterschied zwischen diesen Wellentypen liegt in ihrer Frequenz und somit ihrer Energie. Bereich Bezeichnung Frequenz Frequenz in Hz 103 Radiowellen Mikrowellen 4 3·105 300 km 4 10 10 kHz 3·10 30 km Langwellen 105 100 kHz 3·103 3 km Mittelwellen 6 10 7 1 MHz 2 300 m 1 3·10 Kurzwellen 10 10 MHz 3·10 30 m Ultrakurzwellen, UKW 108 100 MHz 3·100 3m Dezimeterwellen 109 1 GHz 3·10-1 3 dm Zentimeterwellen, Radar 1010 10 GHz 3·10-2 3 cm Millimeterwellen 1011 100 GHz 3·10-3 3 mm 10 13 1 THz 3·10 -4 300 μm -5 30 μm Fernes Infrarot 10 10 THz 3·10 Nahes Infrarot 1014 100 THz 3·10-6 Sichtbares Licht Ultraviolett Weiche Röntgenstrahlung Röntgenstrahlung Harte Röntgenst. Gammastrahlung Kosmische Strahlung Wellenlänge Längstwellen 12 Lichtartige Strahlung 1 kHz Wellenlänge in m 15 10 16 10 17 10 1018 19 10 20 3·10 300 nm 3·10 -8 30 nm 100 PHz 3·10 -9 3 nm 1 EHz 3·10-10 1 PHz 10 PHz 10 EHz 3·10 300 pm -11 30 pm 3 pm 300 fm 10 100 EHz 3·10 -12 10 1 ZHz 3·10 -13 1022 10 ZHz 3·10-14 30 fm 10 100 ZHz 3·10 3 fm 21 Höhenstrahlung 3 μm -7 23 -15 Zwischen Wellenlänge λ und Frequenz f gibt es den folgenden Zusammenhang: wobei c die Vakuumlichtgeschwindigkeit ist (c = 3· 10 8 m/s). c= λ⋅ f Im elektromagnetischen Frequenzspektrum nimmt das sichtbare Licht einen kleinen Bereich an (400 nm – 750 nm). 11PS – PHYSIK P. Rendulić 2014 OPTIK 33 5.8 Farben und Sinne Farben wie wir sie kennen sind Sinneseindrücke. Dass wir die Farben rein subjektiv empfinden, kann man bei den folgenden Versuchen erkennen. 5.8.1 Versuch 1 Schließe dein linkes Auge mit der Hand und richte deinen Blick auf den schwarzen Punkt im grünen Quadrat. Fixiere den Punkt mit starrem Blick etwa eine Minute lang. Die Farbe scheint zu verblassen. Beobachte dann das grüne Quadrat mit dem linken Auge. Der Farbeindruck scheint jetzt intensiver zu sein. 5.8.2 Versuch 2 Wiederhole den Versuch 1 mit beiden Augen, das heißt, starre den schwarzen Punkt im grünen Quadrat während ungefähr einer Minute an. Richte dann deinen Blick auf den rechten schwarzen Punkt und blinzele mit den Augen. Du siehst jetzt auf dem weißen Hintergrund ein Quadrat in der Komplementärfarbe Magenta. 5.8.3 Versuch 3 Zwei gelbe Zitronen aus Karton werden auf gelben und roten Untergrund gelegt. Man stellt fest, dass der wahrgenommene Farbeindruck der Zitrone vom Hintergrund abhängt. 5.8.4 Schlussfolgerung Die Versuche zeigen, dass die wahrgenommene Farbe von der jeweiligen Situation abhängt. Farben sind Sinneseindrücke. Unterschiedliche Situationen und unterschiedliche Lichtarten bewirken unterschiedliche Farbeindrücke. Physikalisch unterscheiden sich die Farben durch ihre Wellenlänge oder Frequenz. 11PS – PHYSIK 5.9 P. Rendulić 2014 OPTIK 34 Farbensehen 5.9.1 Additive Farbmischung Unter der additiven (lat. hinzufügend) Farbmischung versteht man ein Phänomen, das den vom Auge empfundenen Farbeindruck durch Hinzufügen von Farbreizen beschreibt. Da das Farbensehen beim Menschen mit drei unterschiedlichen Fotorezeptoren, den sogenannten Zapfen in der Netzhaut des Auges stattfindet, können mit drei additiven Grundfarben, alle Farbreize dargestellt werden. Beim Menschen unterscheidet man zwischen den Zapfen vom L-Typ (Rotrezeptor), M-Typ (Grünrezeptor) und STyp (Blaurezeptor). Daher sind die additiven Grundfarben Rot, Grün und Blau. Bei der additiven Farbmischung handelt es sich um ein physiologisches Phänomen (den menschlichen Körper betreffend). 5.9.2 Spektrale Empfindlichkeit des Auges Die sich im Auge befindenden Zapfen sprechen auf unterschiedliche spektrale Bereiche an. Sie tragen zum photopischen Sehen bei (Farbensehen bei Tag). Sie sind maximal empfindlich für Licht der Wellenlängen: • 564 nm: (Gelb)-Rot, • 534 nm: Grün, • 420 nm: Blau Im Auge befinden sich ausserdem noch weitere Fotorezeptoren, die Stäbchen mit einer maximalen Empfindlichkeit bei 498 nm. Die Stäbchen sind besonders lichtempfindlich und tragen zum skotopischen Sehen bei (Nachtsehen, Dämmerungssehen, monochromatisch ohne Farben). 5.9.3 Komplementärfarben Farben sind komplementär, wenn sie gemischt einen Grauton ergeben. Nach dem RGB/CMY Modell sind die folgenden Grundfarben Komplementär: Rot und Cyan # FF 00 00 # 00 FF FF Grün und Magenta # 00 FF 00 # FF 00 FF Blau und Yellow # 00 00 FF # FF FF 00 Im RGB-Modell sind Farben Komplementär wenn ihre Hexadezimalen Zahlenwerte addiert # FF FF FF ergeben. 11PS – PHYSIK P. Rendulić 2014 OPTIK 35 Komplementärfarben werden vom Auge als angenehmes Farb-Paar empfunden. Zwischen beiden Komplementärfarben herrscht auch ein erhöhter Farbkontrast. Dieser Effekt wird oft von Photographen ausgenutzt. 5.9.4 Subtraktive Farbmischung Unter der subtraktiven (lat. entfernen) Farbmischung versteht man die physikalische Farbmischung. Mit der Hilfe von „Filtern“ werden hier nicht die Farben gemischt, sondern es werden Bestandteile des Lichtspektrums durch diese Filter entfernt. Dadurch entstehen unterschiedliche Farbreize im Auge. Die Farben Magenta, Cyan und Gelb sind die Primärfarben der subtraktiven Farbmischung. Das jeweilige Filter entfernt den komplementärfarbigen Spektralbereich aus dem weissen Licht. 5.10 Körperfarben Wenn Licht auf einen Körper trifft, so treten die folgenden Phänomene auf: • Ein Teil des Lichts wird reflektiert. • Ein Teil des Lichts wird absorbiert. • Ein Teil des Lichts wird durch den Körper durchgelassen. Wenn man von einem „Teil“ spricht, so meint man einen Teil der Farben die im Licht enthalten sind. Dementsperchend entstehen die Farben von Körpern, die wir sehen. Wenn man Körper mit unterschiedlichem Licht beleuchtet, so nehmen wir auch unterschiedliche Farben wahr. Beispiele Das Foto zeigt eine Farbtafel die mit Blitzlicht beleuchtet wurde. Die Kamera wurde so eingestellt, um mit Blitzlicht optimale Ergebnisse zu liefern (Weißabgleich Blitzlicht). Wenn bei gleichen Einstellungen an der Kamera Glühlampenlicht verwendet wird zeigt das Foto eine gelbe Verfärbung (Gelbstich). Dies kommt zustande weil „weißes“ Glühlampenlicht weniger Blau- und mehr Gelbanteile besitzt. Wird die Kamera bei Benutzen von Glühlampenlicht entsprechend eingestellt (Weißabgleich Glühlampenlicht) so kann auch mit Glühlampenlicht eine „farbechte“ Aufnahme gelingen. 11PS – PHYSIK P. Rendulić 2014 OPTIK 36 Unsere Augen spielen uns hier oft einen Streich, denn sie passen sich in gewissem Maße an die farblichen Gegebenheiten des Lichts an, sodass wir Weiß stets als Weiß empfinden (automatischer Weißabgleich) und je nach Lichtgegebenheiten die Farben von Körpern unterschiedlich sehen. Digitale Kameras arbeiten meistens mit einem automatischen Weißabgleich (AWG, automatic white balance), damit Aufnahmen farblich so aussehen, wie unser Auge es sehen würde. Es kann jedoch vorkommen, dass bei schwierigen Lichtverhältnissen die Kameraautomatik versagt und Bilder verfärbt aussehen. 5.10.1 Bildschirme Foto von Lego-Mann und Lego-Bagger Makro-Aufnahme von Computer-Bildschirm Bildschirme benutzen leuchtende Punkte der Grundfarben Rot, Grün und Blau um durch additive Farbmischung alle möglichen Farben darzustellen. 5.10.2 Drucker Farbdrucker (Tintenstrahl, Laser) benutzen Pigmente der Grundfarben Cyan, Magenta und Gelb um durch subtraktive Farbmischung alle möglichen Farben darzustellen. 11PS – PHYSIK 6 6.1 P. Rendulić 2014 OPTIK 37 Beugung und Interferenz * Beugung von Licht Wenn man Licht durch einen schmalen Spalt gehen lässt, dann müsste hinter dem Spalt, auf einem Schirm, durch die geradlinige Lichtausbreitung, ein scharf begrenzter Lichtfleck zu sehen sein. Der Versuch zeigt jedoch, dass hinter dem Spalt Licht in allen Richtungen nachweisbar ist. Diese Ablenkung des Lichts aus seiner geradlinigen Ausbreitungsrichtung kann mit dem Modell Lichtstrahl nicht erklärt werden. Nach dem Wellenmodell ist durch das huygensche Prinzip jeder Punkt einer Öffnung, der von der Wellenfront getroffen wird, Ausgangspunkt einer Elementarwelle, die sich nach allen Seiten ausbreitet (→ Beugung des Lichts). Die Ausbreitung des Lichts hinter schmalen Spalten, Kanten und kleinen Hindernissen auch in Schattenräume hinein wird als Beugung bezeichnet. Da die Beugung eine wellentypische Erscheinung ist (sie tritt z.B auch bei Wasserwellen auf), sagt man, dass das Licht Welleneigenschaften hat. 6.2 Interferenz von Licht Wie bei Wasser- oder Schallwellen kann auch bei Lichtwellen das Phänomen der Interferenz beobachtet werden. Unter Interferenz von Licht versteht man die Überlagerung von Lichtwellen mit Bereichen der Verstärkung und der Abschwächung bzw. Auslöschung. Interferenzmuster sind aber nur unter bestimmten Bedingungen beobachtbar. Die zu interferierende Wellen müssen nicht nur die gleiche Frequenz sondern auch eine feste Phasenlage zueinander haben. Man sagt, dass die Wellen kohärent sein müssen. Am einfachsten lässt sich die Interferenz bei kohärentem, monochromatischem Laserlicht beobachten. 6.3 Interferenz am Doppelspalt Wenn man 2 eng benachbarte Spalte mit parallelem, kohärentem und monochromatischem Licht beleuchtet, so können beide Spalte als Zentren von huygenschen Elementarwellen betrachtet werden. Die beiden Wellensysteme überlagern sich und ergeben ein stabiles Interferenzmuster mit Maxima (hell) und Minima (dunkel). 11PS – PHYSIK P. Rendulić 2014 OPTIK 38 6.3.1 Interferenz am Strichgitter Man erhält ein optisches Gitter, wenn man anstatt eines Doppelspalts viele Spalte mit jeweils gleichem Abstand benutzt. Der entscheidende Vorteil des Gitters gegenüber dem Doppelspalt besteht darin, dass die Maxima beim Gitter wesentlich schärfer ausgeprägt sind. Dadurch sind genauere Messungen möglich. Charakteristisch für das Gitter ist die Gitterkonstante. Sie entspricht dem Abstand zweier benachbarter Spalte. Bei einem Gitter hängt die Lage der Interferenzmaxima von der Gitterkonstante b und der Wellenlänge λ ab k⋅ λ sin α k= ( k= 0,± 1,± 2, ...) b Zwischen den Maxima befinden sich breite dunkle Streifen Bei sonst gleichen Parametern hängt der Abstand der Interferenzmaxima von der Wellenlänge λ und somit von der Farbe des Lichts ab. Da rotes Licht eine größere Wellenlänge als blaues Licht besitzt, liegen die Maxima bei Verwendung von rotem Licht weiter auseinander als bei der Verwendung von blauem Licht. Bei der Verwendung von weißem Licht entstehen daher farbige Streifen, die man als Beugungsspektrum bezeichnet. Mit einem Gitter kann Licht in seine farblichen Bestandteile zerlegt werden. 6.3.2 Beisiel: die Compact-Disc Wenn man eine Compact-Disc anschaut, kann man, wenn der Betrachtungswinkel stimmt, das Spektrum der Lichtquelle, welche die CD beleuchtet, gut sehen. Dies kommt dadurch zustande, weil die aus Pits und Lands geformte Spur wie ein Beugungsgitter wirkt. 11PS – PHYSIK 7 P. Rendulić 2014 OPTIK 39 Energiegewinnung aus Sonnenlicht * Die Sonne ist der wichtigste Energielieferant der Erde und der Motor des Klimas und des Lebens. Da die Reserven an fossilen Brennstoffe langsam aber sicher immer geringer werden ist es wichtig, die direkt verfügbare Sonnenernergie so schnell wie möglich auszunutzen. Möglich ist dies durch den Solarkollektor und die Solarzelle. 7.1 Solarkollektor Der Solarkollektor ermöglicht es, die im Sonnenlicht enthaltene Wärmestrahlung auszunutzen, um kaltes Wasser zu erwärmen. Das warme Wasser kann dann im Sanitärbereich genutzt werden (Warmwasser zum Baden oder zum Heizen). Das folgende Schema zeigt Warmwasseraufbereitung, den Aufbau einer thermischen Solaranlage zur Die thermische Solaranlege besteht aus mehreren Kreisen. Im Solarkreis zirkuliert eine Flüssigkeit, welche die von den Kollektoren aufgefangenen Wärme aufnimmt und sie in den Kombispeicher führt. In diesem Speicher wird dann durch diese Wärme Kaltwasser für das Bad erwärmt. Die Wärme wird aber auch genutzt, um das Wasser im Kreislauf der Raumheizung zu erwärmen. Für den Fall, wo die Kollektoren dem Kombispeicher nicht genug Wärme zufügen können (z. B im Winter bei niedrigem Sonnenstand, oder bei starker Bevölkung) steht ein Heizkessel zur Verfügung, welcher dann für die Warmwasszubereitung einspringt. Dieser kann durch Gas, Heizöl, Holz, Kohle, Bricketts, etc. befeuert werden. 11PS – PHYSIK 7.2 P. Rendulić 2014 OPTIK 40 Solarzelle Die Solarzelle oder photovoltaische Zelle ermöglicht es, durch die im Sonnenlicht enthaltene Energie elektrischen Strom zu erzeugen. Der Strom kann entweder direkt genutzt werden, ins Stromnetz eingespeist werden oder in Akkumulatoren gespeichert werden. Das folgende Schema zeigt den Aufbau einer photovoltaischen Solaranlage zur Stromerzeugung. Im gezeigten Fall wird der erzeugte Strom in das öffentliche Stromnetz eingespeist. 7.3 Aufgaben 7.3.1 Notwendigkeit der Energiegewinnung aus Sonnenlicht Erkläre, warum es wichtig ist, die im Sonnenlicht enthaltene Energie intensiv zu nutzen! 7.3.2 Vor- und Nachteile der Solaranlagen Welche Vor- und welche Nachteile siehst du in der Energiegewinnung aus Sonnenlicht? Wie kann man den Einfluss der Nachteile minimieren?