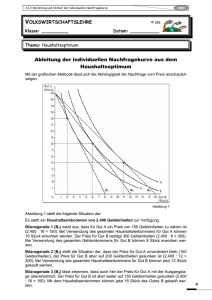
Aufgabe 1 (12 Punkte) Horsts Nutzenfunktion ist gegeben durch U !x

Aufgabe 1 (12 Punkte)
Horsts Nutzenfunktion ist gegeben durch
U (x1 ; x2 ) = x21 + 4x22 .
Dabei steht x1 für die von ihm konsumierte Menge von Gut 1 und x2 für die von ihm
konsumierte Menge von Gut 2. Der Preis einer Einheit von Gut 1 beträgt p1 > 0 und der
Preis einer Einheit von Gut 2 genau 2 Geldeinheiten. Horst besitzt 8 Geldeinheiten.
a) Bestimmen Sie die Grenzrate der Substitution! Wie ändert sich diese mit steigendem
x1 ?
b) Bestimmen Sie das Haushaltsoptimum! Hinweis: Nehmen Sie eine Fallunterscheidung
vor!
c) Zeichnen Sie die Nachfragekurve für Gut 1!
Lösung
a) Die Grenzrate der Substitution beträgt:
@U
@x1
@U
@x2
=
x1
2x1
=
.
8x2
4x2
Entlang einer Indi¤erenzkurve nimmt x2 mit steigendem x1 ab. Eine Senkung von x2
und ein Anstieg von x1 führen zu einem Anstieg von M RS. Aufgrund dessen sind
Horsts Präferenzen konkav.
b) Da Horsts Präferenzen konkav sind, kommt nur ein Randoptimum als Lösung in Frage.
Konsumiert Horst nur Gut 1, kann er maximal p81 Einheiten von Gut 1 konsumieren.
Konsumiert Horst nur Gut 2, kann er maximal 4 Einheiten von Gut 2 konsumieren.
Horsts Nutzen beträgt entweder
U
8
;0
p1
=
8
p1
2
oder
U (0; 4) = 64.
Demnach konsumiert Horst nur Gut 1, wenn gilt (es sind nur positive Mengen möglich):
8
p1
2
8
p1
p1
Demnach ist
8
p1 ; 0
Haushaltsoptima
> 64
> 8
< 1
das Haushaltsoptimum für p1 < 1. Für p1 = 1 gibt es zwei
8
p1 ; 0
und (0; 4). Für p1 > 1 lautet das Haushaltsoptimum (0; 4).
1
p
1
1
x
8
1
Aufgabe 2 (12 Punkte)
Erik muss sein Taschengeld von 32 auf die beiden Güter Schokolade und Lakritzstangen
aufteilen. Der Preis für eine Tafel Schokolade betrage zunächst pS = 1, der für eine Stange
1
1
Lakritz pL = 1. Eriks Nutzenfunktion sei U (S; L) = S 2 L 6 :
(a) Berechnen Sie die optimalen Mengen an Süß
igkeiten!
(b) Der Staat bemüht sich um eine gesündere Jugend und erhöht den Preis für Schokolade
auf 2 Euro. Beschreiben Sie gra…sch die Veränderung zum neuen optimalen Konsumbündel! Zeichnen Sie insbesondere den Einkommens- und den Substitutionse¤ekt für
Schokolade ein! Hinweis: Nutzen Sie, dass für Preise pS = 2 und pL = 1 und bei
einem Budget von 56 das optimale Konsumbündel (21; 14) beträgt!
Lösungsvorschlag:
(a) Variante a)
3
1
Nutzenfunktion ist äquivalent zu U (S; L) = S 4 L 4
L
=
S
=
1m
=8
4 1
3m
= 24
4 1
Variante b)
M RS
=
L =
1
1
1
2 L3
2S
2
1 12
3
6S L
1
S
3
Eingesetzt in die Budgetbedingung:
2
=3
L !
1
= M OC =
S
1
1
S+ S
3
1
S+ S
3
S
L
=
32
=
32
=
=
24
8
(b) Budget, falls man sich altes Optimum leisten will:
msub
=
=
2 24 + 1 8
56
Zur gra…schen Lösung wurde damit das Hilfsoptimum gegeben (S H ; LH ) = (21; 14);
womit bereits der Substitutionse¤ekt bereits eingezeichnet werden kann.
Nun wird das Optimum mit neuen Preisen aber altem Budget bestimmt:
S neu;
=
Lneu;
=
3m
= 12
4 2
1m
=8
4 1
Zeichnung:
L
EE
SE
32
21,14
12,8
24,8
16
3
28
32
S
Aufgabe 3 (7 Punkte)
(a) In einer Welt mit den beiden Gütern Gut 1 und Gut 2 gibt es zwei Güterbündel:
A
Bündel A : xA
1 = 4; x2 = 9;
B
Bündel B : xB
1 = 5; x2 = 3:
Die Preise der Güter sind p1 = 1 und p2 = 3: Einem Agenten steht ein Budget in Höhe
von 30 Geldeinheiten zur Verfügung. Die Präferenzen werden durch die Nutzenfunktion u (x1 ; x2 ) = 2x1 + x2 repräsentiert.
Welches Güterbündel präferiert der Haushalt?
(b) Kreuzen Sie an! Hinweis: Es ist jeweils eine Antwort korrekt.´
In welcher Einheit wird die Konsumentenrente gemessen?
Gramm
Nutzeneinheiten
Geldeinheiten/Mengeneinheit
Geldeinheiten
o
o
o
o
Welche Formel zum Berechnen der Produzentenrente P R ist korrekt ?
PR = E
PR = E
PR = E
C
CF ix
Cvar
o
o
o
Wo liegt eine äquivalente Variation vor?
Welche Mindestsumme verlangen Sie dafür, dass die Verbesserung nicht eintritt?
Was verlangen Sie mindestens als Entschädigung für eine Verschlechterung?
Lösungsvorschlag
(a)
u (4; 9) = 17
u (5; 3) = 13
17 > 13
Er präferiert GB A.
(b) Richtige Antworten:
Geldeinheiten
PR = E
Cvar
Welche Mindestsumme verlangen Sie dafür, dass die Verbesserung nicht eintritt?
4
o
o
Aufgabe 4 (5 Punkte)
Ein Unternehmen besitzt die Produktionsfunktion
3
1
y = f (x1 ; x2 ) = x15 x23 :
(a) Bestimmen Sie die Grenzproduktivität des zweiten Produktionsfaktors!
(b) Bestimmen Sie die Produktionselastizität des zweiten Produktionsfaktors!
Lösungsvorschlag:
(a) Die Grenzproduktivität des zweiten Produktionsfaktors ist die partielle Ableitung der
Produktionsfunktion nach diesem Faktor:
M P2 =
@f (x1 ; x2 )
1 3 2
= x15 x2 3 :
@x2
3
(b) Nach entsprechender De…nition ist die Produktionselastizität wie folgt gegeben:
"y;x2
=
@y
@x2
x2
y
x2
= M P2
3
5
1
x1 x23
3
=
1 5
3 x1 x2
3
5
2
3
x2
1
3
x1 x2
5
=
1
:
3
Aufgabe 5 (7 Punkte)
Ein (gewinnmaximierender) Monopsonist produziert gemäßder Produktionsfunktion:
y = f (x) =
1
x:
4
Dabei bezeichnet y die beim Einsatz von x Einheiten des Produktionsfaktors erstellte Ausbringungsmenge. Die inverse Angebotsfunktion des Produktionsfaktors lautet:
w (x) =
1
x + 1:
3
w (x) steht für den Faktorpreis, der beim Einsatz von x Einheiten des Produktionsfaktors
zu entrichten ist. Der Preis für das Produkt auf dem Absatzmarkt wird durch den Monopsonisten nicht beein‡usst und beträgt 12.
Bestimmen Sie die optimale Einsatzmenge des Produktionsfaktors und den Preis, den der
Monopsonist dabei für diesen entrichtet!
Lösungsvorschlag:
Variante 1:
Die Gewinnfunktion des Monopsonisten lautet:
(x)
= p f (x) x w (x)
1
1
x x
x+1
= 12
4
3
1 2
= 3 x
x
x
3
Diese Funktion maximiert der Monopsonist, indem er die optimale Einsatzmenge des Produktionsfaktors bestimmt:
d
=
dx
x =
2 !
x=0
3
2
3:
Durch Einsetzen in die inverse Angebotsfunktion ergibt sich der Preis, den der Monopsonist
für den Produktionsfaktor entrichtet:
w (3) =
1
3 + 1 = 2:
3
Variante 2:
Im Gewinnoptimum gilt:
!
M R M Px = M Cx
!
p M Px = M Cx
2
1
12
= x+1
4
3
x=3
1
w (3) =
3 + 1 = 2:
3
6
Aufgabe 6 (4 Punkte)
Ein Unternehmen besitzt die Produktionsfunktion
y = f (x) = x2 :
Bestimmen Sie die Grenzkosten des Unternehmens!
Lösungsvorschlag
p
Man bestimmt die Kostenfunktion mittels x (y) = y und
C (y)
= w1 x1
p
= w1
y:
Ableiten gibt die Grenzkostenfunktion
M C = C 0 (y) =
7
1
w1 y
2
1
2
:
Aufgabe 7 (6 Punkte)
Betrachten Sie das folgende Spiel:
Spieler 2
a
b
c
(7; 6)
(2; 5)
d
(4; 0)
(1; 3)
Spieler 1
(a) Ist für den Zeilenwähler Strategie c eine dominante Strategie? Begründen Sie, indem
Sie die relevante(n) Ungleichung(en) angeben!
(b) Ist die Strategiekombination (c; b) ein Nash-Gleichgewicht? Begründen Sie, indem Sie
die relevante(n) Ungleichung(en) angeben!
Lösungsvorschlag
(a) Ja, da 7 > 4 und 2 > 1:
(b) Nein, da 6 < 5 (die Angabe 2 > 1 ist nicht relevant im engsten Sinne).
8
Aufgabe 8 (7 Punkte)
Zwei Unternehmen sind die einzigen Produzenten auf einem Markt mit der inversen Nachfragekurve p(Y ) = 60 5Y: Die Kostenfunktion für das erste Unternehmen sei gegeben
durch C1 (y1 ) = 15y12 ; die Kostenfunktion des anderen Unternehmens sei gegeben durch
C2 (y2 ) = 10y22 :
(a) Berechnen Sie die Reaktionsfunktion von Unternehmen 1 im simultanen Mengenwettbewerb!
(b) Angenommen das zweite Unternehmen würde den Markt verlassen. Wie hoch wäre
nun die Produktion des ersten Unternehmens? Hinweis: Verwenden Sie Aufgabe a)
Lösungsvorschlag:
(a) Gewinnfunktion aufstellen
1 (y1 ; y2 )
= 60y1
5(y1 + y2 )y1
15y12
Partielle Ableitung bilden und Nullsetzen
@
1 (y1 ; y2 )
@y1
= 60
10y1
!
5y2
30y1 = 0
Au‡ösen und Reaktionsfunktion bestimmen
40y1
=
60
3
=
2
y1R (y2 )
5y2
y2
8
(b) Variante 1:
Falls das zweite Unternehmen den Markt verlässt, dann ist y2 = 0 zu wählen und in
die Reaktionsfunktion einzusetzen. Unternehmen 1 bietet demnach y1 = 32 Einheiten
an.
Variante 2:
Falls das zweite Unternehmen den Markt verlässt, ist dies gleichbedeutend, dass Unternehmen 1 Monopolist auf dem Markt ist. Entsprechend lautet die Gewinnfunktion:
1 (y1 ; y2 )
= 60y1
5y12
15y12
Nullsetzen der ersten Ableitung liefert:
d
1 (y1 )
dy1
y1
=
60
=
3
:
2
9
!
40y1 = 0
Aufgabe 9 (12 Punkte)
Gegeben sei die Lotterie 95; 105; 21 ; 12 . Betrachten Sie zur Analyse der Lotterie die folgende
Abbildung:
vNM Nutzenfunktion
[I]
[III]
95
[II]
Geldauszahlung
105
(a) Wahr oder falsch?
wahr
falsch
Die dargestellte vNM-Nutzenfunktion gibt Risikoaversion wieder.
p
Die vNM-Nutzenfunktion u(x) = x gibt Risikoaversion wieder.
Die vNM-Nutzenfunktion u(x) = x2 gibt Risikofreude wieder.
Die vNM-Nutzenfunktion u(x) = 2x2 + 4 gibt Risikoaversion
wieder.
(b) Ordnen Sie für die oben dargestellte vNM-Nutzenfunktion korrekt zu, indem Sie in
jeder Spalte (nicht Zeile!) ein Kreuz setzen!
[I]
[II]
[III]
CE (L)
E (L)
u (105)
u (95)
u (E (L))
Eu (L)
(c) Nehmen Sie nun die vNM-Nutzenfunktion
u (x) = ax2 + c; a > 0
an und bestimmen Sie das Sicherheitsäquivalent der Lotterie 2; 3; 54 ; 15 !
Lösungsvorschlag
wahr
(a)
Die dargestellte vNM-Nutzenfunktion gibt Risikoaversion wieder.
p
Die vNM-Nutzenfunktion u(x) = x gibt Risikoaversion wieder.
Die vNM-Nutzenfunktion u(x) = x2 gibt Risikofreude wieder.
Die vNM-Nutzenfunktion u(x) = 2x2 + 4 gibt Risikoaversion
wieder.
10
falsch
x
x
x
x
(b)
[I]
CE (L)
E (L)
u (105)
u (95)
u (E (L))
Eu (L)
[II]
[III]
x
x
x
(c) Zunächst gilt
4
u (2) +
5
1
4
=
a22 + c +
5
5
= a5 + c;
Eu (L) =
also ist wegen
1
u (3)
5
a32 + c
2
Eu (L) = u (CE (L)) = a (CE (L)) + c
p
CE (L) = 5:
11
Aufgabe 10 (8 Punkte)
In einem Gutshaus gibt es sechs Wohnungen, die jeweils von einer Person bewohnt werden.
Um den Zufahrtsweg zum Gutshaus zu verschönern, überlegen sich die Mieter eine Allee zu
errichten. Alle Mieter haben die gleiche Präferenzordnung bezüglich des Einp‡anzens von
Bäumen am Zufahrtsweg und einem privaten Gut. Die Präferenzordnung
eines einzelnen
p
Mieters i kann durch die Nutzenfunktion U (Xi ; B) = Xi + B dargestellt werden, wobei
Xi die Mengen des privaten Gutes und B die Anzahl an Bäumen ist. Der Preis des privaten
Gutes beträgt 100 und der Preis eines Baumes 50.
Wie viele Bäume sollten gep‡anzt werden?
Lösung
Es handelt sich um konvexe Präferenzen der Mieter, deshalb gilt:
6
X
!
M RSi = M OC
=
M RSi
=
i=1
6
p
2 B
p
B
B
=
=
=
50
100
M UB
=
M UXi
50
100
600
100
36:
12
1
p
2 B
1
1
= p
2 B