Aufgabenblatt 7: Monopol, Natürliches Monopol

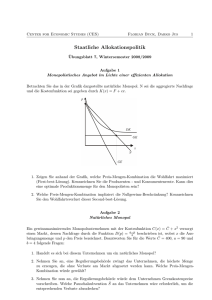
Center for Economic Studies (CES)
Nadjeschda Arnold, Christian Beermann
Ressourcenallokation und Wirtschaftspolitik
Wintersemester 2010 / 2011
Aufgabenblatt 7
Aufgabe 1
Besteuerung und Subventionierung im Monopol
Ein lokales Monopol stehe einer Preis-Absatz-Funktion von p(x) = 12 − 23 x gegenüber und produziere
mit variablen Kosten in Höhe von K(x) = 2x.
1. Berechnen Sie den Gewinn des Monopolisten. Um wie viel liegt der Monopolpreis über dem
Konkurrenzpreis?
2. Nehmen Sie an, der Staat interveniert nun auf dem Monopolmarkt und verlangt eine Mengensteuer in Höhe von τ . Berechnen Sie den Monopolpreis und die Monopolmenge in Abhängigkeit
von der Steuer. Wie hoch darf die Steuer maximal sein, damit der Monopolist seine Produktion
nicht einstellt?
3. Nehmen Sie an, der Staat möchte seine Steuereinnahme aus der Monopolbesteuerung maximieren. Welchen Steuersatz τ ∗ wird der Staat festsetzen und welche Marktallokation wird sich
folglich ergeben? Fertigen Sie auch eine exakte Abbildung an.
4. Wie sich in Teilaufgabe 3. gezeigt hat, wird der Monopolist bei Besteuerung die angebotene
Menge einschränken und nicht ausdehnen. Welche Strategie muss der Staat verfolgen, wenn er
den Monopolisten dazu bringen möchte die Pareto-optimale Menge herzustellen?
Center for Economic Studies (CES)
Nadjeschda Arnold, Christian Beermann
Aufgabe 2
Monopolistisches Angebot im Lichte einer effizienten Allokation
Betrachten Sie das in der Grafik dargestellte natürliche Monopol. N sei die aggregierte Nachfrage und
die Kostenfunktion sei gegeben durch K(x) = F + cx.
1. Zeigen Sie anhand der Grafik, welche Preis-Mengen-Kombination die Wohlfahrt maximiert (Firstbest-Lösung). Kennzeichnen Sie die Produzenten - und Konsumentenrente. Kann dies eine optimale Produktionsmenge für den Monopolisten sein?
2. Welche Preis-Mengen-Kombination impliziert die Nullgewinn-Beschränkung? Kennzeichnen Sie
den Wohlfahrtsverlust dieser Second-best-Lösung.
Aufgabe 3
Natürliches Monopol
Ein gewinnmaximierendes Monopolunternehmen mit der Kostenfunktion C(x) = C +x2 versorgt einen
Markt, dessen Nachfrage durch die Funktion D(p) = a−p
b beschrieben ist, wobei x die Ausbringungsmenge und p den Preis bezeichnet. Beantworten Sie für die Werte C = 400, a = 90 und b = 4 folgende
Fragen:
1. Handelt es sich bei diesem Unternehmen um ein natürliches Monopol?
2. Nehmen Sie an, eine Regulierungsbehörde zwingt das Unternehmen, die höchste Menge zu erzeugen, die ohne Verluste am Markt abgesetzt werden kann. Welche Preis-Mengen-Kombination
würde gewählt?
3. Nehmen Sie nun an, die Regulierungsbehörde würde dem Unternehmen Grenzkostenpreise vorschreiben.
Welche Pauschalsubvention S an das Unternehmen wäre erforderlich, um die entsprechenden
Verluste abzudecken?
Center for Economic Studies (CES)
Nadjeschda Arnold, Christian Beermann
Aufgabe 4
Multiple Choice
Kreuzen Sie die jeweils richtige Antwort an.
1. Ein natürliches Monopol ist dadurch gekennzeichnet, dass
(a) die Durchschnittskosten mit steigender Produktionsmenge fallen.
(b) die Grenzkosten mit steigender Produktionsmenge fallen.
(c) es einer Interessensgruppe gelungen ist, Wettbewerbsbeschränkungen durchzusetzen.
(d) sich die Grenzkosten für jedes Produktionsniveau unterscheiden, da immer ein entsprechender Fixkostenanteil einkalkuliert werden muss.
2. Eigenschaften des natürlichen Monpols
(a) Ein natürliches Monopol ist immer durch fallende Grenzkosten im relevanten Bereich gekennzeichnet.
(b) Da im Fall des natürlichen Monopols die ”Grenzkosten = Preis” Regel gilt, sinkt mit steigender Ausbringungsmenge der Preis.
(c) Es kommt im natürlichen Monopol zu einer Unterversorgung mit dem produzierten Gut,
da der Monopolist im Gewinnmaximum den Preis gleich den Durchschnittskosten setzt.
(d) Bei zunehmenden Skalenerträgen in der Produktion sind Verluste des Monopolisten eine
notwendige Bedingung für gesamtgesellschaftliche Effizienz.