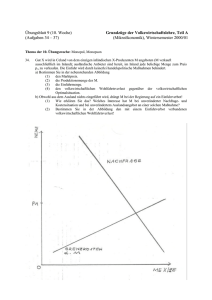
Kostenfunktion im natürlichen Monopol Die Kostenfunktion C(x)

1
Aufgabe 1.1: Kostenfunktion im natürlichen Monopol
Die Kostenfunktion C(x) weise Skalenvorteile bei der Produktion von x auf. Zeige, dass
Grenzkostenpreise nicht kostendeckend sind. Erläutern Sie Ihr Ergebnis auch graphisch.
Antwort zu Aufgabe 1.1
Zu zeigen ist, daß Grenzkosten kleiner sind als die tatsächlichen Kosten bzw. der Monopolist bei Grenzkostenpreisen keinen Gewinn macht:
p=
dC !
< C(x)
dx
!
bzw. π < 0
Die Gewinnfunktion des Unternehmens lautet in diesem Fall
dC
x − C(x)
dx
Zusätzlich ist angenommen, daß Skalenvorteile vorliegen, also:
π = px − C(x) =
C(x)
x
·
dx
dC
>
1
⇔
C(x)
x
>
dC
dx
⇔
C(x)
>
dC
dx x
⇔
dC
dx x
<
0
− C(x)
q.e.d.
Aufgabe 1.2: Kostenfunktion im natürlichen Monopol
Muß ein natürliches Monopol im Einproduktfall notwendig Skalenvorteile aufweisen?
Antwort zu Aufgabe 1.2
Nein, Subadditivität (als Voraussetzung für ein natürliches Monopol) erfordert nicht notwendigerweise Skalenvorteile. Man betrachte z.B.die Kostenfunktion C(x) = 5 + (x − 3)2 an
der Stelle x0 = 5 in Hinblick auf Skalenvorteile und Subadditivität:
Skalenvorteile?
(5−3)2
5
Durchschnittskosten:
C(5)
5
=
Grenzkosten:
dC(x)
x |x0 =5
= 2(5 − 3)
→
keine Skalenvorteile
S=
1,8
2
<1
5
5
+
= 1, 8
=2
P
P
Subadditivität, i.S. v. C( xi ) < C(xi ) ?
Betrachte die Gesamtproduktion von x0 = 5 i.Vgl. zu einer geteilten mit x1 = 2 und x2 = 3
Kosten bei Gesamtproduktion:
Kosten bei geteilter Produktion:
C(5)
C(2) + C(3)
=9
=6+5
= 11
Die Kosten der Gesamtproduktion sind also niedriger als die einer geteilten Produktion.
Daher liegt Subadditivität vor, auch wenn keine Skalenvorteile in Erscheinung treten. (Betrachte in diesem Zusammenhang vor allem die Fixkosten.)
2
Aufgabe 1.3: Kostenfunktion im natürlichen Monopol
1
Betrachten Sie die Kostenfunktion C(x1 , x2 ) = (x1 x2 ) 3 . Prüfen Sie die Kostenfunktion
auf i) Skalenvorteile ii)Verbundvorteile und iii) Subadditivität!
Antwort zu Aufgabe 1.3
i) Vorliegen von Skalenvorteilen entlang eines Strahls:
S
= P C(x)
∂C(x)
xi
=
=
∂xi
1
(x1 x2 ) 3
2
2
x1 ( 31 x2 (x1 x2 )− 3 )+x2 ( 31 x1 (x1 x2 )− 3
1
(x1 x2 ) 3
1
1
1
1
(x
x
1 2 ) 3 + 3 (x1 x2 ) 3
3
)
=
3
2
>1
⇒ Es liegen Skalenvorteile entlang eines Strahls vor.
ii) Vorliegen von Verbundvorteilen
1
C(x1 , 0) + C(0, x2 ) = 0 < (x1 x2 ) 3 = C(x1 , x2 )
⇒ Es liegen keine Verbundvorteile vor.
iii) Vorliegen von Subadditivität:
Aufgrund der vorangegangenen Ergebnisse zeigt sich, dass die Kostenfunktion nicht die Eigenschaft der Subadditivität erfüllt.
Aufgabe 2.1:
Wir betrachten eine Industrie, die ein natürliches Monopol ist. Die Kostenfunktion in der
Industrie ist durch C(x) = F + cx, mit F > 0 und c > 0 gegeben, wobei x die Menge
des in der Industrie angebotenen Gutes ist. Der Nutzen der Verbraucher sei gegeben durch
U = U0 − px und der Gewinn des Monopolisten ist π = (p − c)x(p) − F , wobei die Marktnachfrage x(p) im Preis fällt; also dx/dp < 0 gilt. Die soziale Wohlfahrt, W, ist definiert
durch W := U + π mit dU/dp = −x.
i) Charakterisieren Sie den wohlfahrtsoptimalen Ramsey-Preis. ii) Charakterisieren Sie nun
den gewinnmaximierenden Preis des unregulierten Monopolisten. iii) Inwiefern unterscheiden sich Ihre Ergebnisse unter i) und ii), und warum ist das so.
(Verwenden Sie für die Eigenpreiselastizität den Ausdruck |ηx,p | := −(dx/dp)(p/x).)
Antwort zu Aufgabe 2.1
i) Wohlfahrt unter der Bedingung, daß Monopolist keinen Verlust macht
Aufstellen der Lagrange-Funktion
⇔
W =U +π
L(p, λ)
u.d.B.
=
=
=
π≥0
U + π + λπ
U + (1 + λ)π
U + (1 + λ)(p − c)x − F
Maximierungsbedingung (FOC, Betrachten der inneren Lösung):
3
∂L
∂p
c) dx
dp
=
−x + (1 + λ)(x + (p − c) dx
dp )
=
x(−1 + 1 + λ)
⇔
−(1 + λ)(p −
⇔
p−c
=
⇔
p−c
p
p−c
p
=
λ x
− 1+λ
dx
dp
x dp
λ
−
1+λ
p dx
=
λ
1
1+λ |ηx,p |
⇔
!
=
0
|: p
ii) Maximiere den Profit des Monopolisten:
π
= (p − c)x − F
⇔
dπ
dx
=
⇔
p−c
=
⇔
p−c
p
=
dp
dx x + p − c = 0
dp
− dx
x
1 dp x
− dx
=
p
ηx,p |: p
iii) In beiden Fällen ergibt sich ein Preisaufschlag abhängig von der Eigenpreiselastizität.
λ
Das Ergebnis unterscheidet sich um den Faktor 1+λ
für den Fall von wohlfahrtsoptimalen
Preisen. Diese sind daher niedriger als monopolistisch gesetzte Preise. Ein Vergleich der Gewinne kann diesen Unterschied erklären: Maximieren der Wohlfahrt führt zu Nullgewinn der
Firmen, während Profitmaximierung diesen zu Lasten der Gesamtwohlfahrt steigert.
Aufgabe 2.2:
Unterstellen Sie nun den Fall eines natürlichen Monopolisten, der zwei Güter x1 und x2
produziert...
Antwort zu Aufgabe 2.2
Bei unabhängigen Nachfragen ergeben sich folgende Ramsey-Aufschläge für die beiden
Güter:
∂C
p1 − ∂x
1
p1
=
∂C
p2 − ∂x
2
p2
=
Umformen nach
⇔
λ
1+λ
1 ηx ,p 1 1
λ
1 1+λ ηx ,p λ
1+λ
2
λ
1+λ
=
2
(Gut x1 )
(Gut x2 )
und gleichsetzen:
∂C
p1 − ∂x
1
p1
· |ηx1 ,p1 |
=
∂C
p2 − ∂x
2
p2
· |ηx2 ,p2 |
Entsprechend bestimmt sich der relative Preisaufschlag auf die Grenzkosten eines Gutes
über seine Eigenpreiselastitzität: Bei unabhängigen Nachfragen gilt, daß die jeweiligen mit
der Elastitzität multiplizierten Aufschläge übereinstimmen müssen.
4
Aufgabe 2.3:
Unterstellen Sie nun die folgenden linearen Nachfragen:...
Antwort zu Aufgabe 2.3
Zu zeigen:
x1
∂C
∂x1
− x1
x2
=
x1
∂C
∂x2
− x2
x2
Gegeben:
x1 (p1 ) = a1 − bp1
x2 (p2 ) = a2 − bp2
Preise und Nachfrageveränderung aufgrunddessen:
p1
=
p2
=
a1
b1
a2
b2
−
−
x1
b1
x2
b2
dx1
dp1
dx2
dp2
= −b1
= −b2
Ramsey-Preisaufschläge:
∂C
p1 − ∂x
1
p1
1 p1
· (− dx
dp1 ) x1
=
Kürzen von pi und einsetzen von (2):
h
i
a1
x1
1
0
b1 − b1 − C (x1 ) b1 x1
=
∂C
p2 − ∂x
2
p2
h
a2
b2
−
2 p2
· (− dx
dp2 ) x2
x2
b2
i
− C 0 (x2 ) b2 x12
Weiteres Umformen ergibt dann:
a1 −b1 ·C 0 (x1 )−x1
x1
=
a2 −b2 ·C 0 (x2 )−x2
x2
∂C
x1 ( ∂x
)−x1
1
x1
=
∂C
x2 ( ∂x
)−x2
2
x2
=
q.e.d.
Es bedeutet, dass die relativen Abweichungen der Nachfrage bei Ramsey-Preisen von den
nachgefragten Mengen zu Grenzkostenpreisen gleich groß sind. Damit ist die prozentuale
Mengenverschiebung beider Güter identisch.
Aufgabe 2.4:
Unterstellen Sie nun, dass die Kostenfunktion gegeben ist durch C(x1 , x2 ) = 1000 + x1 + x2
und die Nachfragen durch x1 (p1 ) = 500 − 10p1 und x2 (p2 ) = 1000 − 20p1 . Berechnen Sie die
Ramsey-Preise und Ramsey-Mengen für dieses Beispiel.
Antwort zu Aufgabe 2.4
(Ramsey-Preisansatz, da wg. der Fixkosten Grenzkostenpreise nicht kostendeckend sind.)
Bestimmen der inversen Nachfrage und der Nachfrageveränderung im Preis:
x1 (p1 ) = 500 − 10p1
x2 (p2 ) = 1000 − 20p2
⇔
5
p1 (x1 ) = 50 −
p2 (x2 ) = 50 −
1
10 x1
1
20 x2
(1)
(2)
und
∂x1
∂p1
∂x2
∂p2
= −10
(3)
= −20
(4)
Ramsey-Gewinnbedingung:
π(x1 , x2 ) = p1 x1 + p2 x2 − C(x1 , x2 ) = 0
Einsetzen von (1),(2),(3),(4):
= 50x1 −
= 49x1 −
π(x1 , x2 )
1
2
10 (x1 )
1
2
10 (x1 )
+ 50x2 −
+ 49x2 −
1
2
20 (x2 )
1
2
20 (x2 )
− 1000 − x1 − x2
− 1000
Verwenden des Zusammenhangs aus Aufg. 2.3:
⇔
490−x1
x1
490
x1 − 1
490
x1
=
⇔
2x1
= x2
⇔
=
=
980−x2
x2
980
x2 − 1
980
x2
Einsetzen des Ergebnisses in Ramsey-Gewinnbedingung:
49x1 −
1
2
10 (x1 )
+ 49x2 −
⇔
3 2
x1 + 147x1 − 1000
− 10
⇔
x21
− 490x −
1
2
20 (x2 )
10000
3
Lösen der quadratischen Gleichung:
1.Möglichkeit:
q
+
x1 = 245 − 2452 +
10000
3
⇒ x11 < 0
⇒ x11 = 0 = x21
(Beachte Nebenbedingung für Produktion : x1 ≥ 0)
2.Möglichkeit:
→ x12 = 496, 71 ≈ 497
→
x22 = 994
→
p1 = 0, 3 = p2
− 1000
=
0
=
0
=
0
6
Aufgabe 2.5:
Unterstellen Sie nun, dass die Nachfragen nach den Gütern voneinander abhängig sind.
Antwort zu Aufgabe 2.5
∂xi
∂pj
>
0
if
γ < 0, also sind Güter Substitute.
∂xi
∂pj
<
0
if
γ > 0, also sind Güter Komplemente.
Aufgabe 2.6:
Leiten Sie die Bestimmungsgleichungen für die Ramsey-Aufschläge bei von Null verschiedenen Kreuzpreiselastizitäten her.
(Hinweis: ∂U/∂p1 = −x1 und ∂U/∂p2 = −x2 )
Antwort zu Aufgabe 2.6
Bestimmen des wohlfahrtsoptimalen Preises bei Produktabhängigkeiten:
i. Aufstellen der Lagrangefunktion:
⇔
W =U +π
L(p, λ)
π≥0
U (p1 , p2 ) + π + λπ
U (p1 , p2 ) + (1 + λ)π
U (p1 , p2 ) + (1 + λ)(p1 x1 + p2 x2 − C(x1 , x2 ))
u.d.B.
=
=
=
⇔
ii. Maximierungsbedingungen(FOC, innere Lösung):
1. Ableiten nach p1 :
∂L
∂p1
h
i
∂x2
∂C ∂x1
∂C ∂x2
1
−x1 + (1 + λ) x1 + p1 ∂x
+
p
−
−
2
∂x
∂x
h
∂p1
∂p1
1 ∂p1
2 ∂p1i
∂x1
∂C
∂C
2
−x1 + (1 + λ) x1 + p1 − ∂x1 ∂p1 + p2 − ∂x2 ∂x
∂p1
=
=
!
=
p1
p1 ,
0
λ
Nach − 1+λ
auflösen. Beim verbleibenden Term (Ausdruck in Klammern) ersten Teil mit
zweiten Teil mit pp11 pp22 xx22 erweitern:
⇔
λ
− 1+λ
∂C
p1 − ∂x
1
=
∂C
p1 − ∂x
1
=
p1
∂x1
∂p1
·
1
x1
· ηx1 ,p1 +
· pp11 + p2 −
∂C
p2 − ∂x
2
p2
∂C
∂x2
· ηx2 ,p1 ·
∂x2
∂p1
·
1
x1
·
p1
p1
·
p2
p2
x2 p2
x1 p1
2. Ableiten nach p2 :
∂L
∂p2
=
h
i
∂x1
∂C ∂x1
∂C ∂x2
2
−x2 + (1 + λ) x2 + p2 ∂x
∂p2 + p1 ∂p2 − ∂x1 ∂p2 − ∂x2 ∂p2
h
i
∂x2
∂x1
∂C
∂C
−x2 + (1 + λ) x2 + p2 − ∂x
+
p
−
1
∂p
∂x
∂p
2
2
1
2
=
0
=
·
x2
x2
7
λ
− 1+λ
⇔
=
=
∂C
p2 − ∂x
2
∂C
p2 − ∂x
∂x2
∂p2
·
1
x2
· pp22 + p1 −
∂C
p1 − ∂x
· ηx2 ,p2 +
2
p2
∂C
∂x1
· ηx1 ,p2 ·
1
p1
∂x1
∂p2
·
1
x2
·
p1
p1
·
p2
p2
·
x1
x1
p1 x1
p2 x2
Partielle Betrachtung, d.h. kein Einkommenseffekt, ergibt:
∂x1
∂p2
∂x2
∂p1
=
ηx1 ,p2
=
x2 p1
x2 p1
ηx2 ,p1 · xx21 pp21
und analog:
ηx2 ,p1
=
ηx1 ,p2 ·
∂x1
∂p2
·
x1 p2
x1 p2
=
∂x2
∂p1
·
x1 p1
x2 p2
Dies berücksichtigend und gleichsetzen der zwei FOCs ergibt:
∂C
p1 − ∂x
1
p1
∂C
p1 − ∂x
1
p1
· ηx1 ,p1 − ηx1 ,p2 pp12 xx12
· (ηx1 ,p1 − ηx2 ,p1 )
=
=
∂C
p2 − ∂x
2
p2
∂C
p2 − ∂x
2
p2
· ηx2 ,p2 − ηx2 ,p1 pp21 xx21
· (ηx2 ,p2 − ηx1 ,p2 )
Aufgabe 2.7:
Wie verändern sich die Ramsey-Aufschläge bei Substituten und Komplementen gegenüber
dem Fall unabhängiger Güter?
Antwort zu Aufgabe 2.7
(
ηxi ,pj < 0
ηxi ,pj > 0
d.h. Substitutionalität, folglich höherer Preisaufschlag
d.h. Komplementarität, folglich niedrigerer Preisaufschlag
Aufgabe 2.8
Nennen Sie Argumente, die gegen eine Verwendung von Ramsey-Preisen als Regulierungsregel für ein natürliches Monopol sprechen.
Antwort zu Aufgabe 2.8
Informationserfordernisse und Effizienzbetrachtungen (s. weitere Aufgaben)