1. Rotation um eine feste Achse
Werbung
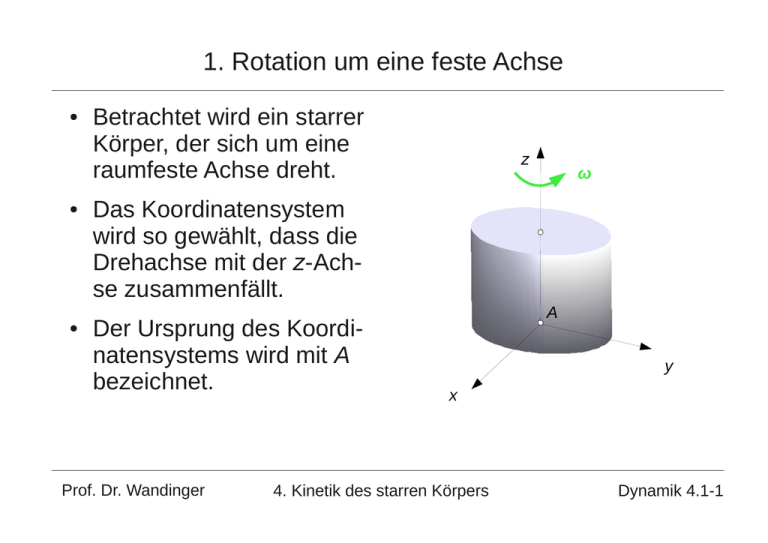
1. Rotation um eine feste Achse ● ● ● Betrachtet wird ein starrer Körper, der sich um eine raumfeste Achse dreht. z ω Das Koordinatensystem wird so gewählt, dass die Drehachse mit der z-Achse zusammenfällt. Der Ursprung des Koordinatensystems wird mit A bezeichnet. Prof. Dr. Wandinger A y x 4. Kinetik des starren Körpers Dynamik 4.1-1 1. Rotation um eine feste Achse 1.1 Schwerpunktsatz 1.2 Drallsatz 1.3 Massenträgheitsmoment 1.4 Zentrifugalmomente 1.5 Arbeit und Energie 1.6 Massenpunkt und starrer Körper Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-2 1.1 Schwerpunktsatz ● Schwerpunktsatz: – – Am freigeschnittenen Körper greift die resultierende äußere Kraft F und die resultierende Lagerkraft A an. Prof. Dr. Wandinger rS ω Wie bei einem System von Massenpunkten gilt: m r̈ S = F A F y A A 4. Kinetik des starren Körpers S x Dynamik 4.1-3 1.1 Schwerpunktsatz ● Dynamisches Gleichgewicht: – Aus dem Schwerpunktsatz folgt: F A−m r̈ S =0 – Mit r̈ S = a S = ̇× r S × × r S folgt daraus: F A−m ̇× r S −m × ×r S =0 – Die Trägheitskraft T =−m ̇× r S wird durch die Bahnbeschleunigung verursacht. – Die Trägheitskraft Z=−m × ×r S wird durch die Zentripetalbeschleunigung verursacht. Sie wird als Zentrifugalkraft bezeichnet. – Das dynamische Gleichgewicht lautet: F AT Z=0 Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-4 1.1 Schwerpunktsatz ● Statische Unwucht: – Wenn die Drehachse durch den Schwerpunkt geht, sind wegen r S =0 die Trägheitskräfte null. Die Lagerkräfte sind im Gleichgewicht mit den äußeren Kräften. – Bei Körpern, die sich mit großer Winkelgeschwindigkeit drehen, sollte daher der Schwerpunkt auf der Drehachse liegen. – Liegt der Schwerpunkt nicht auf der Drehachse, so spricht man von statischer Unwucht. – Ist ein Rad statisch ausgewuchtet, so ist es in jeder Lage im statischen Gleichgewicht. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-5 1.2 Drallsatz ● Drall: – z Aus dem Grenzübergang zu infinitesimalen Massenelementen folgt für den Drall: ω vP L A =∫ r P ×v P dm dm K – Für die Vektoren gilt: r P = x e x y e yz e z v P =v Px e x v Py e y A rP y x Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-6 1.2 Drallsatz – Das Vektorprodukt berechnet sich zu r P ×v P = x e x y e y z e z × v Px e x v Py e y = x v Py − y v Px e z z v Px e y−z v Py e x – Jeder Massenpunkt bewegt sich auf einer Kreisbahn um die z-Achse. Daher gilt für seine Geschwindigkeit: v Px =− y , v Py= x – Damit berechnet sich der Integrand zu r P ×v P = x 2 y 2 e z −y z e y −x z e x Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-7 1.2 Drallsatz – Integration über den Körper ergibt: L A = – 2 2 x y dm e z −∫ x z dm e x−∫ y z dm e y ∫ K K K Definitionen: ● Massenträgheitsmoment: J z =∫ x y dm=∫ r dm 2 K ● Deviationsmomente: 2 K J xz =−∫ x z dm , J yz =−∫ y z dm K ● 2 K Die Deviationsmomente werden auch als Zentrifugalmomente bezeichnet. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-8 1.2 Drallsatz – Ergebnis: ● Bei einer Drehung um die z-Achse gilt für die Komponenten des Dralls: L Ax = J xz L Ay = J yz L Az = J z ● ● Nur wenn die Deviationsmomente null sind, stimmt die Richtung des Drallvektors mit der Richtung der Drehachse überein. In einem körperfesten System ändern sich Jxz, Jyz und Jz nicht. Der Drallvektor dreht sich mit dem Körper. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-9 1.2 Drallsatz – Beispiel: ● z ● ω Der Schwenkarm dreht sich mit der Winkelgeschwindigkeit ω = 1s-1 um die z-Achse. Massenträgheitsmoment: J z =5 kgm ● 2 Deviationsmomente: 2 J xz =−7,5 kgm , J yz =0 LA ● A Prof. Dr. Wandinger x Komponenten des Drallvektors: 2 2 L Ax =−7,5 kgm / s , L Ay =0 kgm / s 2 L Az =5 kgm / s 4. Kinetik des starren Körpers Dynamik 4.1-10 1.2 Drallsatz ● Drallsatz: – Für ein System von Massenpunkten lautet der Drallsatz: L̇ A = M A – Der Drallsatz behält seine Gültigkeit beim Grenzübergang auf ein System aus unendlich vielen unendlich kleinen Massenelementen. – Bei einer Drehung um die z-Achse bewegt sich jeder Punkt des starren Körpers auf einer Kreisbahn um die z-Achse. – Dabei ändern sich sein Abstand r von der z-Achse sowie seine z-Koordinate z nicht. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-11 1.2 Drallsatz – Für die z-Komponente des Dralls gilt daher: L̇ Az =J z ̇= M Az – Dabei ist MAz das Moment der äußeren Kräfte um die z-Achse. – Wenn das Moment der äußeren Kräfte null ist, gilt der Drallerhaltungssatz: J z 2= J z 1 2 =1 Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-12 1.2 Drallsatz – Die x- und y- Koordinaten der Punkte des starren Körpers ändern sich bei einer Drehung um die z-Achse. – Daher ändern sich die Deviationsmomente. – Für die Momente um die x- und y-Achse folgt aus dem Drallsatz: M = L̇ =̇ J J̇ Ax Ax xz xz M Ay = L̇ Ay =̇ J yz J̇ yz – Da sich die Punkte auf einer Kreisbahn um die z-Achse bewegen, gilt: ẋ=v Px =− y , ẏ=v Py = x Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-13 1.2 Drallsatz – Damit folgt für die zeitliche Änderung der Deviationsmomente: J̇ xz =−∫ ẋ z dm= ∫ y z dm=− J yz K K J̇ yz =−∫ ẏ z dm=−∫ x z dm= J xz – Ergebnis: K K M Ax =̇ J xz −2 J yz M Ay =̇ J yz 2 J xz M Az =̇ J z Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-14 1.2 Drallsatz – Das Moment MAz um die Drehachse verursacht eine Winkelbeschleunigung. – Die Momente MAx und MAy sind auch bei konstanter Winkelgeschwindigkeit von null verschieden. Sie sind notwendig, um die Drehachse in ihrer Richtung zu halten, wenn die Deviationsmomente nicht null sind. – Dieser Effekt wird als dynamische Unwucht bezeichnet. – Der Drallsatz stellt eine Beziehung zwischen den am Körper angreifenden Momenten und der Winkelgeschwindigkeit her. Er wird daher auch als Momentensatz bezeichnet. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-15 1.2 Drallsatz – In einem ortsfesten Koordinatensystem sind die Deviationsmomente zeitlich veränderlich. – In einem Koordinatensystem, das sich mit dem Körper dreht, sind die Deviationsmomente zeitlich konstant. Die Komponenten des berechneten Moments beziehen sich dann ebenfalls auf das körperfeste Koordinatensystem. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-16 1.2 Drallsatz – Beispiel: ● ● z Der Schwenkarm wird um 90° um die z-Achse gedreht. Für 0 ≤ t ≤ T gilt für den Winkel: t t = 1−cos 4 T ω ● Winkelgeschwindigkeit: 2 t t =̇t = sin 4T T A x ● Winkelbeschleunigung: 3 t ̇t = 2 cos T 4T Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-17 1.2 Drallsatz ● Im mitrotierenden Koordinatensystem gilt mit Jyz = 0 für die Momente: 3 t J xz M Ax t =̇t J xz = cos 2 4 T T 4 J xz 2 t 2 M Ay t = t J xz = sin 16 T 2 T 3 t Jz M Az t= cos 2 4 T T ● Zahlenwerte: Prof. Dr. Wandinger 2 T =2 s , J z =5 kgm , J xz =−7,5 kgm 4. Kinetik des starren Körpers 2 Dynamik 4.1-18 1.2 Drallsatz Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-19 1.2 Drallsatz Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-20 1.3 Massenträgheitsmoment ● Definition: – Das Massenträgheitsmoment ist definiert durch a J a =∫ r 2 dm K – – Dabei ist r der senkrechte Abstand zur Drehachse. Bei einer Drehung um die z-Achse gilt: r P J z =∫ r 2 dm=∫ x 2 y 2 dm K Prof. Dr. Wandinger K 4. Kinetik des starren Körpers Dynamik 4.1-21 1.3 Massenträgheitsmoment ● Homogener Körper: – Bei einem homogenen Körper ist die Dichte ρ konstant. – Mit dm= dV folgt: J z =∫ r 2 dm=∫ r 2 dV K – V Wenn die Dicke h des homogenen Körpers konstant ist, folgt mit dV =h dA : J z = h ∫ r 2 dA= h I p A – 2 Dabei ist I p =∫ r dA das polare Flächenträgheitsmoment. A Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-22 1.3 Massenträgheitsmoment ● Beispiel: Propeller y b Dicke h L x S – Der Koordinatenursprung wird in den Schwerpunkt gelegt. – Der Propeller dreht sich um die z-Achse. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-23 1.3 Massenträgheitsmoment – Massenträgheitsmoment: L J z = h∫ x 2 y 2 dA= h ∫ A L = h ∫ −L [ ] 2 2 x y dy dx −L −b /2 [ 3 y=b /2 y 2 x y 3 x3 b2 = h b x 3 12 – [∫ b /2 ] ] y=−b/ 2 x =L L dx= h ∫ −L 3 b b x2 dx 12 2 2 3 2 2 2 b = h b L b L = h b L L 2 3 12 3 4 x =−L Mit der Masse m=2 h b L folgt: [ ] 1 b 2 J z = m L 1 3 2L Prof. Dr. Wandinger 2 1 ≈ m L 2 für b≪ L 3 4. Kinetik des starren Körpers Dynamik 4.1-24 1.3 Massenträgheitsmoment ● Beispiel: Kreisscheibe y Dicke h dA=2 r dr R J z = h ∫ r 2 dA=2 h∫ r 3 dr dr A R x r dA Prof. Dr. Wandinger 0 4 r =R [] r =2 h 4 1 = m R2 2 4. Kinetik des starren Körpers 1 = h R4 2 r =0 Dynamik 4.1-25 1.3 Massenträgheitsmoment ● Beispiel: Rechteck Dicke h y J z = h∫ x 2 y 2 dA x b A a/ 2 = h [ b/ 2 2 2 x y dy ∫ ∫ −a/ 2 −b /2 a/ 2 = h ∫ −a/ 2 [ [ x 3 b2 = h b x 3 12 Prof. Dr. Wandinger 3 y=b/ 2 y x y 3 2 ] a dx ] ] y=−b/ 2 x=a /2 a /2 dx= h ∫ −a /2 b3 x b dx 12 2 a3 b2 1 = h b a = m a 2 b 2 12 12 12 x=−a / 2 4. Kinetik des starren Körpers Dynamik 4.1-26 1.3 Massenträgheitsmoment ● Satz von Steiner: – – z Massenträgheitsmomente und Deviationsmomente für Achsen durch den Schwerpunkt sind für viele elementare Körper tabelliert. Z zS S Y Sie lassen sich leicht auf parallel in einen anderen Punkt verschobene Achsen umrechnen. xS A X x Prof. Dr. Wandinger m 4. Kinetik des starren Körpers yS y Dynamik 4.1-27 1.3 Massenträgheitsmoment x= X x S , y=Y y S , z=Z z S – Für die Koordinaten gilt: – Daraus folgt: 2 2 2 2 x y = X x s Y y s = X 2 2 x S X x 2S Y 2 2 y S Y y 2s x z= X x S Z z S = X Z x S Z z S X x S z S y z= Y y S Z z S =Y Z y S Z z S Y y S z S – Aus der Definition des Schwerpunkts folgt: ∫ X dm=∫ Y dm=0 K – K Damit liefert die Integration über den Körper: J Az =∫ x 2 y2 dm=∫ X 2 Y 2 dm x 2S y 2S m=J Sz r 2S m K Prof. Dr. Wandinger K 4. Kinetik des starren Körpers Dynamik 4.1-28 1.3 Massenträgheitsmoment – Entsprechend folgt für die Deviationsmomente: J Axz =−∫ x z dm=−∫ X Z dm− x S z S m=J Sxz − x S z S m K K J Ayz =−∫ y z dm=−∫ Y Z dm− y S z S m=J Syz −y S z S m K – K Ergebnis: (Satz von Steiner) J Az = J Sz x 2S y 2S m J Axz = J Sxz − x S zS m J Ayz = J Syz − yS z S m Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-29 1.3 Massenträgheitsmoment ● Massenpunkte: – Da ein Massenpunkt keine Ausdehnung hat, sind sein Massenträgheitsmoment und seine Deviationsmomente bezüglich dem Punkt, an dem er sich befindet, null. – Befindet sich der Massenpunkt am Punkt P, so folgt aus dem Satz von Steiner für das Massenträgheitsmoment und die Deviationsmomente bezüglich Punkt A: J Az = J Axz = J Ayz = Prof. Dr. Wandinger 2 2 x y P P m −x P z P m −y P z P m 4. Kinetik des starren Körpers Dynamik 4.1-30 1.3 Massenträgheitsmoment ● Trägheitsradius: – Ein Massenpunkt der Masse m im Abstand iz von der Drehachse hat das gleiche Massenträgheitsmoment wie ein starrer Körper der Masse m, wenn gilt: – Der Abstand iz heißt Trägheitsradius. – Beispiele: ● Kreisscheibe: ● Prof. Dr. Wandinger 2 Rechteck: Jz m i =J z i z = m 2 z 2 R 2 iz= = R 2 2 4. Kinetik des starren Körpers a b iz= 12 2 Dynamik 4.1-31 1.3 Massenträgheitsmoment ● Zusammengesetzte Körper: – Das Massenträgheitsmoment eines aus elementaren Körpern zusammengesetzten Körpers lässt sich durch Addition der Massenträgheitsmomente der einzelnen Körper ermitteln. – Dabei können auch Körper subtrahiert werden. – Es ist darauf zu achten, dass alle Massenträgheitsmomente mit dem Satz von Steiner auf den gemeinsamen Bezugspunkt umgerechnet werden. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-32 1.3 Massenträgheitsmoment ● Beispiel: Schlagbaum 0,5 0,25 A 0,25 4 1 0,5 3 0,25 2 1 1,5 2,5 0,5 3 Dicke h1 = 0,2 Dicke h2 = 0,1 Alle Maße in m Dichte ρ = 2700kg/m3 Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-33 1.3 Massenträgheitsmoment – Zu berechnen ist das Massenträgheitsmoment des Schlagbaums um den Drehpunkt A. – Der Schlagbaum besteht aus dem quaderförmigen Ausgleichsgewicht 1 und der quaderförmigen Schranke 2 mit den beiden kreisförmigen Löchern 3 und 4. – Körper 1: Ausgleichsgewicht ● ● ● 3 Masse: m1 =1 m⋅0,5 m⋅0,2 m⋅2700 kg/ m =270 kg Massenträgheitsmoment bezogen auf Schwerpunkt: 1 2 2 2 2 2 J S 1= ⋅270 kg⋅ 1 m 0,5 m =28,13 kgm 12 Massenträgheitsmoment bezogen auf Drehpunkt: 2 2 2 J 1 =28,125 kgm 0,5 m ⋅270 kg=95,63 kgm Prof. Dr. Wandinger 4. Kinetik des starren Körpers 2 Dynamik 4.1-34 1.3 Massenträgheitsmoment – Körper 2: Schranke ohne Löcher ● ● ● Masse: 3 m2 =3 m⋅0,5 m⋅0,1 m⋅2700 kg /m =405 kg Massenträgheitsmoment bezogen auf Schwerpunkt: 1 2 2 2 2 2 J S 2 = ⋅405 kg⋅ 3 m 0,5 m =312,2 kgm 12 Massenträgheitsmoment bezogen auf Drehpunkt: 2 2 2 J 2 =312,2 kgm 1,5−0,25 m ⋅405 kg=945 kgm Prof. Dr. Wandinger 4. Kinetik des starren Körpers 2 Dynamik 4.1-35 1.3 Massenträgheitsmoment – Körper 3: Loch 2 0,25 2 3 m ⋅0,1 m⋅2700 kg/ m =13,25 kg 2 m3 =⋅ ● Masse: ● Massenträgheitsmoment bezogen auf Schwerpunkt: 1 2 2 2 J S 3 = ⋅13,25 kg⋅0,125 m =0,10 kgm 2 ● Massenträgheitsmoment bezogen auf Drehpunkt: 2 2 2 J 3=0,10 kgm 1,5−0,25 m ⋅13,25 kg=20,81 kgm Prof. Dr. Wandinger 4. Kinetik des starren Körpers 2 Dynamik 4.1-36 1.3 Massenträgheitsmoment – Körper 4: Loch m 4 =m3 =13,25 kg ● Masse: ● Massenträgheitsmoment bezogen auf Schwerpunkt: J S 4=J S 3=0,10 kgm ● 2 Massenträgheitsmoment bezogen auf Drehpunkt: 2 2 2 J 4 =0,10 kgm 2,5−0,25 m ⋅13,25 kg=67,20 kgm – Gesamt: 2 J =J 1J 2 −J 3−J 4 2 2 2 2 J =95,63 kgm 945 kgm −20,81 kgm −67,20 kgm =952,6 kgm Prof. Dr. Wandinger 4. Kinetik des starren Körpers 2 Dynamik 4.1-37 1.4 Zentrifugalmomente ● ● Betrachtet wird ein Körper, der sich mit der konstanten Winkelgeschwindigkeit ω um die z-Achse dreht. Dynamisches Gleichgewicht: – Die Beschleunigung eines Massenpunktes ist a Px =−2 x , a Py =−2 y – Für die Zentrifugalkraft gilt: dZ x =−a Px dm=2 x dm , dZ y =−a Py dm=2 y dm Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-38 1.4 Zentrifugalmomente – z Resultierende Momente: ω M TAx =−∫ z dZ y K =− 2∫ z y dm= 2 J yz K dm z M TAy =∫ z dZ x y K = 2 ∫ z x dm=− 2 J xz A K – x Dynamisches Gleichgewicht: M Ax M TAx =0 : −2 J yz2 J yz =0 ✓ M Ay M TAy =0 : 2 J xz − 2 J xz =0 ✓ Prof. Dr. Wandinger y 4. Kinetik des starren Körpers dZy dZx x Dynamik 4.1-39 1.4 Zentrifugalmomente – Die Fliehkraftmomente versuchen, die Drehachse zu kippen. – Um die Drehachse festzuhalten, sind die äußeren Momente M Ax =−M TAx , M Ay =−M TAy nötig. – Im ortsfesten Koordinatensystem hängen diese Momente von der Zeit ab, da die Deviationsmomente von der Zeit abhängen. – In einem mitrotierenden körperfesten Koordinatensystem sind die Deviationsmomente zeitlich konstant. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-40 1.4 Zentrifugalmomente ● Symmetrische Körper: – Spiegelsymmetrie bezüglich der xy-Ebene: ● ● ● Zu jedem Massenelement an der Stelle (xi , yi , zi) gibt es ein entsprechendes Massenelement an der Stelle (xi , yi , -zi). Die Momente der Fliehkraft um die x- und y-Achse heben sich jeweils gegenseitig auf. z ω Zi zi S x xi -zi Zi Daher sind die resultierenden Zentrifugalmomente null. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-41 1.4 Zentrifugalmomente – Achsensymmetrie bezüglich der z-Achse: ● ● ● ● y Bei einer Drehung um 180° um die z-Achse wird der Körper auf sich selbst abgebildet. Zi yi Zu jedem Massenelement an der Stelle (xi , yi , zi) gibt es ein entsprechendes Massenelement an der Stelle (-xi , -yi , zi). Die zugehörigen Zentrifugalkräfte heben sich gegenseitig auf. -xi ω xi x -yi Zi Daher sind die resultierenden Zentrifugalmomente null. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-42 1.4 Zentrifugalmomente – Zyklische Symmetrie bezüglich der z-Achse: ● ● ● Bei einer Drehung um den Winkel φ um die z-Achse wird der Körper auf sich selbst abgebildet. y Zi Zi Die Zentrifugalkräfte an entsprechenden Massenelementen bilden ein zentrales Kraftsystem, das im Gleichgewicht ist. Die Zentrifugalmomente sind null. Prof. Dr. Wandinger x Zi 4. Kinetik des starren Körpers Zi Dynamik 4.1-43 1.4 Zentrifugalmomente ● – Für einen Winkel von 180° ergibt sich die Achsensymmetrie. Rotationssymmetrie bezüglich der z-Achse: ● ● ● Bei einer Drehung um einen beliebigen Winkel um die z-Achse wird der Körper auf sich selbst abgebildet. Die Rotationssymmetrie ist ein Spezialfall der zyklischen Symmetrie. Daher sind die Zentrifugalmomente null. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-44 1.4 Zentrifugalmomente ● Auswuchten: – – Durch Anbringen von zwei Ausgleichsmassen wird erreicht, dass das Rad statisch und dynamisch ausgewuchtet ist. Die x- und y-Koordinaten der beiden Massen werden so bestimmt, dass der Schwerpunkt auf der Drehachse liegt und die beiden Zentrifugalmomente verschwinden. Prof. Dr. Wandinger 4. Kinetik des starren Körpers m z m Dynamik 4.1-45 1.5 Arbeit und Energie ● Arbeit eines Kräftepaares: dW = F a d = M d a L F – Für die Leistung gilt: Prof. Dr. Wandinger dr 1=L d dr 2 = La d dr2 dr1 dφ dW = F dr 2 −F dr 1 B W AB=∫ M d F A dW d P= =M =M dt dt 4. Kinetik des starren Körpers Dynamik 4.1-46 1.5 Arbeit und Energie ● Kinetische Energie bei Rotation: – – – 1 2 Kinetische Energie eines Massenelementes: dE = v dm 2 1 Mit v 2=2 x 2 y 2 folgt: dE K = 2 x 2 y2 dm 2 K Integration über den Körper ergibt die gesamte kinetische Energie: 1 1 2 2 2 E = ∫ x y dm = J z 2 2K 2 K Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-47 1.5 Arbeit und Energie ● Arbeitssatz: – Bei starren Bindungen verrichten die inneren Kräfte keine Arbeit. – Damit folgt aus dem Arbeitssatz für Massenpunktsysteme unmittelbar der Arbeitssatz für einen starren Körper, der um eine feste Achse rotiert: E KB −E KA =W AB Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-48 1.5 Arbeit und Energie – Die Differenz zwischen der kinetischen Energie zum Zeitpunkt B und der kinetischen Energie zum Zeitpunkt A ist gleich der während dieser Zeit vom resultierenden Moment der äußeren Kräfte verrichteten Arbeit. – Der Arbeitssatz gilt auch für Systeme aus starren Körpern. Dabei ist über die kinetischen Energien aller Körper sowie über die an allen Körpern von den äußeren Kräften verrichteten Arbeiten zu summieren. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-49 1.5 Arbeit und Energie ● Beispiel: Bremse L F a ω JA Prof. Dr. Wandinger A r 4. Kinetik des starren Körpers Dynamik 4.1-50 1.5 Arbeit und Energie – Die Trommel mit dem Massenträgheitsmoment JA dreht sich mit der Winkelgeschwindigkeit ω0 um den Punkt A. – Sie wird durch einen Bremshebel zum Stillstand gebracht. – Am Bremshebel greift die konstante Kraft F an. – Der Reibungskoeffizient zwischen Bremse und Trommel ist μ. – Nach wie vielen Umdrehungen kommt die Trommel zum Stillstand? Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-51 1.5 Arbeit und Energie Bremskraft: – L P F a R N ∑ M P=0 : R A a N −L F =0 L N= F a r L R= N = F a Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-52 1.5 Arbeit und Energie – – Kinetische Energie der Trommel: ● Bei Bremsbeginn: 1 K 2 E 0 = J A 0 2 ● Am Ende des Bremsvorgangs: E E =0 K Arbeit der äußeren Kräfte: ● ● An der Trommel greift die konstante Reibkraft R an. Zugehöriges Bremsmoment: M B =r R ● Arbeit des Bremsmoments: ● φB : während des Bremsvorgangs überstrichener Winkel Prof. Dr. Wandinger W 0 E =−M B B 4. Kinetik des starren Körpers Dynamik 4.1-53 1.5 Arbeit und Energie – Arbeitssatz: E KE −E 0K =W 0 E 1 − J A 20 =−M B B 2 J A 20 J A 20 a B= = 2 MB 2r LF – Während einer Umdrehung wird ein Winkel von 2π überstrichen. – Daher gilt für die Anzahl der Umdrehungen bis zum Stillstand: B J A 20 a N B= = 2 4r L F Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-54 1.5 Arbeit und Energie ● Energieerhaltungssatz: – Wenn an einem starren Körper nur konservative Kräfte angreifen, dann gilt: E KB E PB =E KA E PA – Der Satz gilt auch für ein System aus starren Körpern, zwischen denen starre Bindungen vorliegen. – Dabei ist über kinetischen Energien aller Körper und die potenziellen Energien aller am System angreifenden konservativen Kräfte zu summieren. Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-55 1.5 Arbeit und Energie ● Beispiel: – Auf einer homogenen Scheibe der Masse m2 ist ein dehnstarres Seil aufgewickelt. – An dem Seil hängt über eine masselose Rolle die Masse m1. – Das System ist anfangs in Ruhe. – Gesucht ist die Geschwindigkeit der Masse m1 in Abhängigkeit vom zurückgelegten Weg. Prof. Dr. Wandinger 4. Kinetik des starren Körpers m2 r m1 Dynamik 4.1-56 1.5 Arbeit und Energie – – Der Weg s der Masse m1 und der Winkel φ der Masse m2 werden ab der Ruhelage gemessen. m2 A φ Kinetische Energie: ● ● ● K E 0 =0 Ruhelage: 1 1 2 Ausgelenkte Lage: E = J A ̇ m1 ṡ 2 2 2 1 2 Mit J A = m2 r gilt: 2 1 1 K 2 2 2 Es = m2 r ̇ m1 ṡ 2 2 K s Prof. Dr. Wandinger m1 s 4. Kinetik des starren Körpers Dynamik 4.1-57 1.5 Arbeit und Energie – Arbeit der äußeren Kräfte: ● ● ● – Die einzige äußere Kraft, die Arbeit verrichtet, ist die Gewichtskraft. Als Bezugspunkt für die Lageenergie wird die Ruhelage gewählt. Dann gilt für die Lageenergie in der Ruhelage und in der ausgelenkten Lage: G G E 0 =0, E s =−m1 g s Kinematik: ● Die Änderung der freien Seillänge ist gleich der Länge des abgespulten Seils: ṡ 2 s=r ̇=2 r Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-58 1.5 Arbeit und Energie – Energieerhaltungssatz: E sK E Gs = E K0 E G0 =0 1 1 m 2 r 2 ̇ 2m1 ṡ 2 −m1 g s=0 2 2 2 1 ṡ 2 m2 r 2 m1 ṡ 2 =2 m1 g s 2 r 2 m1 g s 2 m 2 m1 ṡ =2 m1 g s ṡ=v= 2 m 2m1 2 Prof. Dr. Wandinger 4. Kinetik des starren Körpers Dynamik 4.1-59 1.6 Massenpunkt und starrer Körper Eindimensionale Bewegung des Massenpunkts Weg s Rotierender starrer Körper Winkel Geschwindigkeit v= ṡ Winkelgeschwindigkeit Beschleunigung a= v̇= s̈ Winkelbeschleunigung ̇=̈ =̇ Masse m Massenträgheitsmoment J z Kraft F Moment Prof. Dr. Wandinger 4. Kinetik des starren Körpers Mz Dynamik 4.1-60 1.6 Massenpunkt und starrer Körper Eindimensionale Bewegung des Massenpunkts Impuls p=m v Impulssatz Drall Drallsatz F=m v̇ 1 Kinetische Energie E = m v 2 2 dW = F ds Arbeit K Leistung P=F v Prof. Dr. Wandinger Rotierender starrer Körper L z= J z M z =J z ̇ 1 Kinetische Energie E = J z 2 2 dW = M z d Arbeit K Leistung 4. Kinetik des starren Körpers P= M z Dynamik 4.1-61