Übungsblatt 0 (Muster)

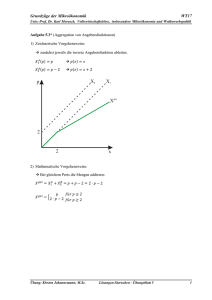
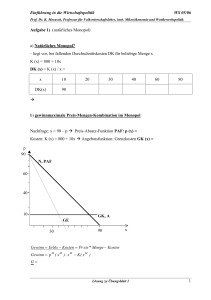
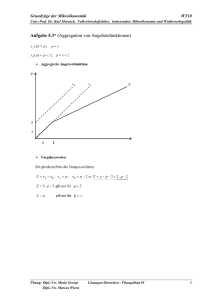
Mikroökonomie II: Allokationstheorie und Wettbewerbspolitik
FT07
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
Übungsaufgabe 1 (Mengenwettbewerb bei homogenen Gütern)
Ein Monopolist produziert ein Gut zu konstanten Durchschnittskosten (und damit auch
konstanten Grenzkosten) DK = GK = 5 . Die Marktnachfrage ist durch X = 53 − p gegeben.
(a) Bestimmen Sie Preis, Menge, Gewinn und Konsumentenrente im Gewinnmaximum des
Monopolisten.
(b) Gehen Sie nun davon aus, dass ein zweites Unternehmen mit gleicher Kostenfunktion in
den Markt eintritt. Geben Sie die Gewinne der Unternehmen als Funktionen der Absatzmengen x1 und x 2 an. Ermitteln Sie auf dieser Grundlage zunächst die Reaktionsfunktionen und bestimmen Sie dann graphisch und analytisch das resultierende CournotGleichgewicht.
(c) Gehen Sie nun alternativ zu (b) davon aus, dass das etablierte Unternehmen die Absatzmenge vor dem Neueintreter bindend festlegen kann. Bestimmen Sie das zugehörige
Stackelberg-Gleichgewicht.
(d) Vergleichen Sie Preis, Mengen, Gewinne, Konsumentenrente und Wohlfahrt im Monopol,
Cournot- und Stackelberg-Gleichgewicht mit der Situation bei vollkommenem Wettbewerb.
(e) Betrachten Sie nochmals den Cournot-Fall, gehen Sie aber jetzt davon aus, dass die
Kosten für Unternehmen 2 durch DK = GK = 8 gegeben sind. Wie unterscheidet sich das
Ergebnis vom Cournot-Gleichgewicht mit identischen Wettbewerbern?
Übung: Dipl.-VW Mario Georgi
Übungsblatt #3 (zu 2.1, 2.2, 2.3)
1
Mikroökonomie II: Allokationstheorie und Wettbewerbspolitik
FT07
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
Übungsaufgabe 2 (Preis- und Mengenwettbewerb bei differenzierten Produkten)
Zwei Unternehmen mit konstanten und identischen Grenzkosten GK = 2 und Fixkosten
K f = 10 stehen auf einem Duopolmarkt mit differenzierten Produkten miteinander im
Wettbewerb. Sie sehen sich dabei Nachfragefunktionen der Form xi = 15 − pi + 1 2 p j
gegenüber. (Hinweis: Es ist günstiger mit Brüchen zu rechnen, da sich ansonsten unendliche
Dezimalbrüche und somit Rundungsfehler ergeben.)
(a) Bestimmen Sie die Reaktionskurven und das Nash-Gleichgewicht des Simultanspiels für
den Fall von Preiswettbewerb. Ermitteln Sie auch das Stackelberg-Gleichgewicht (ein Unternehmen kann den Preis zeitlich vor dem Wettbewerber bindend festlegen)!
(b) Welche Ergebnisse würden sich demgegenüber einstellen, wenn die Unternehmen statt der
Preise die Mengen festlegen? Ermitteln Sie zunächst die inversen Nachfragefunktionen
pi = a0 − a1 xi − a2 x j und bestimmen sie dann auf dieser Grundlage die Gleichgewichte des
Cournot-Spiels und des Stackelberg-Spiels!
(c) Vergleichen Sie Preise und Absatzmengen in den vier Situationen! Wie lassen sich diese
unterschiedlichen Ergebnisse ökonomisch interpretieren?
Übungsaufgabe 3 (Strategische Investition im Mengenduopol)
Zwei Unternehmen mit konstanten Durchschnittskosten DK = 2 stehen sich in einem
homogenen Cournot-Duopol mit inverser Nachfragefunktion p = 14 − X gegenüber.
Unternehmen 1 hat die Möglichkeit, durch ein Forschungsprojekt für das Ausgaben in Höhe
von f anfallen, eine neue Technologie mit Kosten DK = 0 zu entwickeln. Die Entscheidung
von Unternehmen 1 über die Durchführung des Forschungsprojekts fällt zeitlich vor der
(simultanen) Festlegung der Absatzmengen und kann von Unternehmen 2 beobachtet werden.
(a) Berechnen und zeichnen Sie die Reaktionsfunktionen und bestimmen Sie die CournotNash-Gleichgewichte sowohl für den Fall mit als auch für den Fall ohne Durchführung des
Forschungsprojekts!
(b) Bis zu welchen Forschungsausgaben f ist für Unternehmen 1 die Durchführung des
Forschungsprojekts vorteilhaft? Wieviel wäre das Unternehmen demgegenüber höchstens
bereit für Forschung auszugeben, wenn sich dadurch an den Absatzmengen nichts ändern
würde? Erklären Sie, warum es zu dieser "Überinvestition" kommt!
Übung: Dipl.-VW Mario Georgi
Übungsblatt #3 (zu 2.1, 2.2, 2.3)
2
Mikroökonomie II: Allokationstheorie und Wettbewerbspolitik
FT07
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
* Übungsaufgabe 4 (Preiswettbewerb mit differenzierten Produkten, strategische Investition)
Die neue Fluggesellschaft „Fly Germany“ tritt in den Markt für Inlandsflüge ein. Sie bietet
zunächst auf der auch von der Lufthansa bedienten Strecke München – Kiel eine Verbindung
an. Da die Flüge nicht zum gleichen Zeitpunkt stattfinden, werden die Angebote der beiden
Fluggesellschaften von den Konsumenten als differenzierte Produkte wahrgenommen. Das
Nachfrage wird durch das symmetrische Nachfragesystem xFG = 900 − 9 pFG + 3 pL und
xL = 900 − 9 pL + 3 pFG beschrieben. Die Kosten auf dieser Strecke seien zunächst für beide
Gesellschaften identisch und betragen jeweils K ( xi ) = 80 xi + 3000 .
a) Bestimmen Sie zunächst die Reaktionsfunktionen der beiden Wettbewerber und zeichnen
Sie diese in ein Reaktionskurvendiagramm ein.
b) Ermitteln Sie nun graphisch und rechnerisch die Gleichgewichtspreise. Berechnen Sie
dann die zugehörigen Mengen und die Gewinne der Fluggesellschaften.
c) Gehen Sie jetzt davon aus, dass es „Fly Germany“ gelingt, die Kosten pro Passagier durch
ein Kostensenkungsprogramm auf 45 Geldeinheiten zu reduzieren, d.h. die
Kostenfunktion von „Fly Germany“ lautet nun K FG ( xFG ) = 45 xFG + 3000 .
Ermitteln Sie die neue Reaktionsfunktion von „Fly Germany“ und zeichnen Sie sie in das
Reaktionskurvendiagramm ein. Bestimmen Sie dann auf dieser Grundlage die
Gleichgewichtspreise und die resultierenden Gewinne der beiden Fluggesellschaften.
Welche Gewinne hätten sich demgegenüber ergeben, wenn die Preise nach der
Kostensenkung unverändert geblieben wären? Erläutern Sie, wodurch die zusätzliche
Gewinnänderung im Duopol verursacht wird und gehen Sie in diesem Zusammenhang
auch auf die unterschiedlichen Anreize zur Kostensenkung in Oligopolen mit Preis- vs.
Mengenstrategien ein.
Übung: Dipl.-VW Mario Georgi
Übungsblatt #3 (zu 2.1, 2.2, 2.3)
3