Preiswettbewerb versus Kollusion

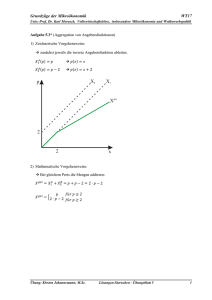
Übung zur Vorlesung Mikroökonomie I
Wintersemester 2005/06
Preiswettbewerb versus Kollusion
Zwei Duopolisten [U1 , U2] produzieren jeweils ein Produkt. Hierbei
handelt es sich um differenzierte Produkte. Die Anbieter haben jeweils Fixkosten F = 20 , ihre variablen Stückkosten ci = 0 . Gegeben
sei die allg. Nachfragefunktion qi ( pi , p j ) = α − β i pi + γ i p j für den
repräsentativen Akteur i, wobei α den Reservationspreis darstellt, βi
die Eigenpreissensitivität der Nachfrage und γi die Preissensitivität
des anderen Preises pj ausdrückt.
a) Nehmen Sie folgende Werte an: α = 12, βi = 2 und γi = 1. Bestimmen Sie die Nachfragefunktionen q1 und q2. Interpretieren Sie die
oben erwähnten Preissensitivitäten. Was passiert mit der Verkaufsmenge, wenn die Preise variieren?
b) Angenommen, die Duopolisten setzen simultan ihre Preise und
nehmen dabei den Preis des Konkurrenten als gegeben hin.
Bestimmen Sie ihre Gewinnfunktionen π i ( pi , p j ) = pi qi − ci qi − F .
c) Bei welchem Preis pi wird πi maximiert? Berechnen Sie hierfür zunächst die Reaktionsfunktionen, anschließend die Gleichgewichts∗
preise ( pi ).
d) Stellen Sie die in Aufgabe c) erlangten Ergebnisse grafisch dar. Wo
liegt das Nash-Gleichgewicht? Was gilt bei dieser Preissetzung für
die Unternehmen?
e) Die Unternehmen haben eine geheime Preisabsprache getroffen.
Anstatt ihre Preise unabhängig voneinander festzulegen, beschließen sie, den gleichen Preis für ihr Produkt zu setzen. Bestimmen
Sie die Funktion, die den Marktgewinn ausweist. Berechnen Sie auf
Basis dessen den Gleichgewichtspreis der Unternehmen sowie den
sich daraus ergebenden Gewinn.
f) Erstellen Sie anhand der in Aufgabe c) und e) erlangten Ergebnisse
eine Auszahlungsmatrix.
g) Überprüfen und interpretieren Sie die vorliegende Situation anhand
der Ihnen bekannten spieltheoretischen Methoden und Ausdrücke.
[Quelle: Pindyck/Rubinfeld (2003): Mikroökonomie, 5. Aufl., Boston et al.: Pearson Studium, S. 616 ff.]