Wettbewerb und Regulierung FT09 Übungsaufgabe 1

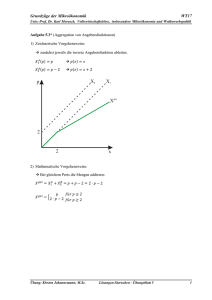
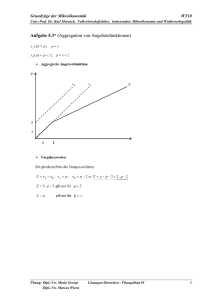
Wettbewerb und Regulierung
FT09
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
Übungsaufgabe 1 (Zusammenhang zwischen Marktstruktur und Marktergebnis)
Gehen Sie von einer Situation mit Marktnachfrage X = 15 − 1 2 p und konstanten Durchschnittskosten DK = 6 aus. Bestimmen Sie den Gesamtabsatz X O ( n ) im Oligopolgleichgewicht für n = 2 , 5 und 11 Unternehmen, sowie den entsprechenden Absatz X W
für die Situation bei vollkommenem Wettbewerb ( p = GK ) . Wie hoch ist jeweils der
prozentualen Wohlfahrtsverlust gegenüber der Situation bei vollkommenem Wettbewerb?
Übungsaufgabe 2 (Unternehmenszusammenschlüsse)
Das Entstehen von Marktmacht durch internes Unternehmenswachstum wird im GWB
zugelassen (nur gegen „Missbrauch von Marktmacht“ wird vorgegangen). Demgegenüber gilt
eine durch Zusammenschluss von Unternehmen (externes Unternehmenswachstum)
entstehende Marktmacht per se als Form der Wettbewerbsbeschränkung. Das folgende
Oligopolbeispiel soll verdeutlichen, wieso diese unterschiedliche Behandlung sinnvoll sein
kann. Zudem soll der allgemein hergeleitete Zusammenhang zwischen Preis-Kosten-Marge
und Herfindahl-Index nochmals an einem konkreten Beispiel veranschaulicht werden.
In einem Markt mit Marktnachfrage X = 80 − p sind drei Unternehmen aktiv. In der
Ausgangssituation ist die Kostenfunktion für alle Unternehmen identisch und durch
K ( x i ) = 64 + 32x i gegeben.
a) Ermitteln Sie die Reaktionsfunktionen und bestimmen Sie dann analytisch das resultierende Cournot-Gleichgewicht. Wie hoch sind Preis, Gewinne, Konsumentenrente und
Wohlfahrt? Bestimmen Sie auch den CR1-Index (Marktanteil des größten Unternehmens),
den Herfindahl-Index H und die Preis-Kosten-Marge. Wie hoch ist die Preiselastizität der
Nachfrage im Cournot-Gleichgewicht?
b) Gehen Sie nun davon aus, dass sich zwei Unternehmen zusammenschließen. Bestimmen
Sie das resultierende Cournot-Gleichgewicht (Duopol-Wettbewerb zwischen dem
fusionierten Unternehmen und dem dritten Wettbewerber)! Wie hoch sind jetzt der CR1und der Herfindahl-Index? Ist der Zusammenschluss für die Unternehmen vorteilhaft,
wenn die Fixkosten des fusionierten Unternehmens gerade der Summe der Fixkosten der
beiden Unternehmen entsprechen? Wie lautet Ihre Antwort, wenn sich die Summe der
Fixkosten durch die Fusion um 25% bzw. 50% reduziert („Synergieeffekte“). Welche
Auswirkung ergibt sich jeweils auf die Wohlfahrt?
c) Gehen Sie nun wieder wie in Teilaufgabe a) von einem Markt mit drei Wettbewerbern
aus. Unternehmen 1 hat jedoch eine überlegene Technologie entwickelt, die es ihm
erlaubt das Gut zu durchschnittlichen variablen Kosten DVK1 = 16 herzustellen (die FixÜbung: Dipl.-Vw Rita Orsolya Toth
Mario Georgi
Übungsblatt #4 (zu 2.4 und 3.1)
1
Wettbewerb und Regulierung
FT09
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
kosten bleiben unverändert). Ermitteln Sie das Cournot-Gleichgewicht dieses asymmetrischen Oligopols. Bestimmen Sie wieder Preis, Gewinne, Konsumentenrente und
Wohlfahrt sowie die Konzentrationsindices. Vergleichen Sie die Ergebnisse mit denen in
den Teilaufgaben a) und b).
Übungsaufgabe 3 (Kartelle und abgestimmtes Verhalten)
Die ursprünglichen Fassung des GWB enthielt nur ein Kartellverbot, d.h. ein Verbot
vertraglich vereinbarter Kollusion. Es zeigte sich jedoch, dass es den Unternehmen häufig
gelang, sich auch ohne vertragliche Regelungen kollusiv zu verhalten. Als Reaktion darauf
wurde das Kartellverbot um ein Verbot abgestimmten Verhaltens erweitert.
a) Gehen Sie von einem Cournot-Duopol mit Preisabsatzfunktion p( X ) = 24 − X und
konstanten Durchschnittskosten DK = 0 aus. Ermitteln Sie das Cournot-Gleichgewicht
und die Kollusionslösung. Bestimmen Sie auf dieser Grundlage die Gewinne für die folgende Auszahlungsmatrix:
Unternehmen 2
Unternehmen 1
Kollusions-Menge
Cournot-Menge
Kollusions-Menge
(π1KK; π2KK)
(π1KC; π2KC)
Cournot-Menge
(π1CK; π2CK)
(π1CC; π2CC)
Gewinn U1 Gewinn U2 (jeweils gerundet)
Welche Strategiekombination wird sich im statischen Spiel einstellen (i) wenn die Unternehmen einen bindenden Vertrag abschließen können, (ii) wenn dies aufgrund des Kartellverbots nicht möglich ist? Ist ein Verbot abgestimmten Verhaltens notwendig?
b) Gehen Sie nun alternativ davon aus, dass die Unternehmen in jeder Periode von neuem
ihre Absatzentscheidung treffen und die Entscheidungen des anderen Unternehmens in der
Vorperiode beobachten konnten. Unternehmen 1 verwendet dabei folgende Strategie
(„Trigger-Strategie“): Beginne in Periode 1 mit „Kollusion“; wähle in den Folgeperioden
ebenfalls „Kollusion“ falls Unternehmen 2 sich bisher immer kollusiv verhalten hat;
wechsle für immer zu „Cournot“ sobald Unternehmen 2 einmal „Cournot“ gewählt hat.
Übung: Dipl.-Vw Rita Orsolya Toth
Mario Georgi
Übungsblatt #4 (zu 2.4 und 3.1)
2
Wettbewerb und Regulierung
FT09
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
Zeigen Sie, dass es im unendlich oft wiederholtem Spiel dann für Unternehmen 2 optimal
ist, immer die Strategie „Kollusion“ zu wählen und somit das kollusive Gleichgewicht
auch ohne bindende Verträge realisiert werden kann. (Hinweis: Ermitteln Sie für eine
Abweichung zur Strategie „Cournot“ in Periode t den in Periode t und t + 1 resultierenden
Gewinn bzw. Verlust gegenüber der Strategie „Kollusion“ )
c) Kann das kollusive Verhalten durch eine solche Strategie auch realisiert werden, wenn die
Unternehmen nur eine endliche Anzahl von Perioden im Markt aktiv sind? (Hinweis:
Ermitteln Sie zunächst die optimale(n) Strategiekombination(en) für die letzte Periode T
und gehen Sie von da aus zu T - 1 über usw.).
d) Das Periodenspiel wird nun dahingehend modifiziert, dass den Spielern als weitere
Möglichkeit die Strategie „Preiskrieg“ zur Verfügung steht. Dabei bietet ein Unternehmen
jede beliebige Menge zu p = GK . Wählt ein Unternehmen diese Strategie, so erzielen alle
Unternehmen einen Gewinn von Null (dies gilt unabhängig von der Strategiewahl des
anderen Unternehmens). Im statischen Spiel stellen dann zwei Strategiekombinationen ein
Nash-Gleichgewicht dar: Beide Spieler wählen die Strategie „Cournot“ bzw. beide Spieler
wählen die Strategie „Preiskrieg“ (Hinweis: In einem Nash-Gleichgewicht kann sich kein
Spieler durch Abweichen von seiner Gleichgewichtsstrategie verbessern solange alle
anderen Spieler ebenfalls ihre Nash-Gleichgewichtsstrategie spielen).
Zeigen Sie, dass in diesem Fall durch die Androhung bei Wechsel des Gegenspielers zur
Strategie „Cournot“ selbst auf die pareto-inferiore Strategie „Preiskrieg“ zu wechseln
auch bei einem endlichen Zeithorizont bis zur Periode T – 1 kollusives Verhalten realisiert
werden kann!
*Übungsaufgabe 4 (Mengenwettbewerb, abgestimmtes Verhalten – Klausuraufgabe FT 2003)
In Lummerland wird Zement ausschließlich von zwei Produzenten – Bauzem und Zemmix –
hergestellt, die zusammen den ganzen inländischen Markt beliefern. Da Baumaterialien
strengen Qualitätsnormen unterliegen, kann Zement als homogenes Gut betrachtet werden.
Die Nachfrage nach Zement beträgt X = 400 − p . Die konstanten Durchschnittskosten der
Zementhersteller sind identisch und belaufen sich auf 40 GE pro Tonne Zement.
a) Ermitteln Sie die Reaktionsfunktionen der beiden Zementproduzenten und bestimmen Sie
dann graphisch und rechnerisch das Cournot-Nash-Gleichgewicht. Wie hoch sind der
Marktpreis und die resultierenden Gewinne der Unternehmen?
Übung: Dipl.-Vw Rita Orsolya Toth
Mario Georgi
Übungsblatt #4 (zu 2.4 und 3.1)
3
Wettbewerb und Regulierung
FT09
Prof. Dr. K. Morasch, Professur für Volkswirtschaftslehre, insbes. Mikroökonomie und Wettbewerbspolitik
b) Wie ändert sich das Marktergebnis (d.h. Produktionsmengen, Preis und
Unternehmensgewinne) gegenüber Teilaufgabe a), wenn Bauzem seine Produktionsmenge
vor Zemmix bindend festlegen kann (Stackelberg-Gleichgewicht)?
c) Der große ausländische Konzern Zemlarge entscheidet sich, ein Zementwerk in
Lummerland zu errichten und damit ebenfalls den inländischen Markt zu beliefern.
Bestimmen Sie das resultierende Cournot-Nash-Gleichgewicht nach dem Markteintritt
von Zemlarge. Gehen Sie dabei davon aus, dass Zemlarge ebenfalls mit konstanten
Durchschnittskosten in Höhe von 40 GE pro Tonne produziert. Erläutern Sie dann kurz
(keine Rechnung!), wie die Absatzmengen der Unternehmen von Ihrem Ergebnis
abweichen würden, wenn Zemlarge über eine verbesserte Technologie verfügen würde,
mit der es Zement zu niedrigeren Grenzkosten als die Wettbewerber herstellen kann.
d) Vor kurzer Zeit hat das Bundeskartellamt ein Kartell in der Zementindustrie aufgedeckt,
das nach Erkenntnissen der Behörde über mehrere Jahre bestanden hat.
(d1) Wenn Zemlarge, Bauzem und Zemmix eine Kartellvereinbarung getroffen hätten,
wie viel würde jedes Unternehmen produzieren? Wie hoch wären in diesem Fall der
resultierende Marktpreis und die Unternehmensgewinne? Zeichnen Sie außerdem in
einem geeigneten Diagramm den Wohlfahrtsverlust ein, der durch die Kartellvereinbarung
im Vergleich zum Cournot-Nash-Gleichgewicht entstehen würde und berechnen Sie, um
wie viel Prozent die Wohlfahrt durch die Kartellbildung verringert wird.
(d2) Kartellverträge sind wettbewerbsrechtlich nicht zulässig. Erläutern Sie kurz die
Anreize zu einer Abweichung von einer nicht bindenden Kartellvereinbarung und
diskutieren Sie dann, wie sich bei wiederholter Interaktion die kollusive Lösung trotzdem
durchsetzen lässt. Welche (Markt-)Faktoren beeinflussen die Erfolgsaussichten einer
Kartellbildung? Wie schätzen Sie vor diesem Hintergrund im konkreten Fall die Chancen
für das Zementkartell ein?
Übung: Dipl.-Vw Rita Orsolya Toth
Mario Georgi
Übungsblatt #4 (zu 2.4 und 3.1)
4