Lösung Übung 1 - Universität Heidelberg

Lösungsblatt 1
Interdisziplinäre Institutionenanalyse
Fachbereich Finanzwissenschaft
Universität Heidelberg
Christian F. Pfeil
Ökonomische Grundlagen
Frage 1 - Bestimmungsfaktoren
• Gruppe 1: individuell kontrollierbare Faktoren
– Zeit für Bildung des Humankapitals
– Zeit zur Verrichtung der Arbeit
– Konsumverzicht zwecks Vermögensaufbau
• Gruppe 2: individuell nicht kontrollierbare Faktoren
– gesellschaftliche Rahmenbedingungen (Wissensstand und Kapitalstock der Volkswirtschaft)
– genetische Veranlagung
– Angebots- und Nachfrageschocks mit dauerhafter Wirkung auf Preise der Produktionsfaktoren
Frage 1 - Situation Lebensbeginn
• anfangs sind beide Gruppen unsicher
• zu Beginn des Arbeitslebens ist die Verwertung der Qualitäten unsicher
• → Einkommensunsicherheit
Frage 1 - Risikoeinstellung
• risikoscheu bzw. -avers (Bsp.: risikobehaftete Finanzanlagen beinhalten Risikoprämie)
Unsicherheit und Risikoaversion sind Gründe für Nachfrage nach Versicherungen, Arbeitslosenversicherung als Beispiel für staatliche Versicherung gegen Einkommensunsicherheit (Wohlfahrtsstaat)
Frage 2a - Annahmen
• ex ante sehr viele identische Individuen
• Lebenseinkommen aus 2 Komponenten:
– h - Erstausstattung mit Humankapital (aktuell in der Gesellschaft kumulierte Wissen, haben alle Individuen gemeinsam)
– - Risiko, Qualifikation verwerten zu können (Arbeitsfähigkeit, Nachfrageschocks Einkommensunsicherheit, individuumsspezifisch)
– Lebenseinkommen: y = h + mit E(y) = h und E() = 0
• Individuen sind risikoscheu bzgl. des Einkommens, d.h. streng konkave Nutzenfunktion
1
EXKURS: konkave Nutzenfunktion
• hohes Einkommen mit c und Wahrscheinlichkeit p
• niedriges Einkommen mit c und Wahrscheinlichkeit (1 − p)
• erwartetes Einkommen: E[c] = pc + (1 − p)c
• Risikoaversion: u(E[c]) = u(pc + (1 − p)c) > pu(c) + (1 − p)u(c) = E[u(c)]
• Grafik 1
Frage 2a - optimaler Wohlfahrtsstaat
• Staat beschrieben durch Steuersatz t mit t ∈ [0, 1] und z (einheitliche Pro-Kopf-Zahlung
an Bürger)
• individueller Konsum: c = (1 − t)y + z
• aufgrund großer Anzahl von Individuen ist Wahrscheinlichkeitsverteilung der Einkommen
(ex ante) gleich Verteilung der tatsächlich realisierten Einkommen (ex post)
• d.h. ex ante erwartetes Einkommen = ex post beobachteten Durchschnittseinkommen
→ E[y] = h
• Budgetbeschränkung Staat: durchschnittliche Staatseinnahmen t · E[y] = t · h gleich ProKopf-Zahlung z, d.h. z = t · h
• Staat maximiert erwarteten Nutzen der Bürger unter Beachtung seiner Budgetbeschränkung
• Konsumniveau eines Bürgers: c = (1 − t)y + t · h = y + t · (h − y)
• ex post: Funktion steigend in t, wenn individuelles Buttoeinkommen h unterdurchschnittlich (y < h) und fallend in t, wenn Bürger überdurchschnittliches Einkommen bezieht
(y > h)
•
δc
δt
> 0, wenn y < h und umgekehrt
• nur Bezieher niedriger Einkommen profitieren
• ex ante: E[u((1 − t)(h + ) + t · h)]
• Nutzenmaximierung unter Beachtung der Budgetbeschränkung:
•
∂E[u]
∂t
=
∂E[u((1−t)(h+)+t·h)]
∂t
• =E[u0 ((1 − t)(h + ) + t · h) · (h + ) · (−1)] + E[u0 ((1 − t)(h + ) + t · h) · (h)]
• =−E[(h + ) · u0 ((1 − t)(h + ) + t · h)] + h · E[u0 ((1 − t)(h + ) + t · h)]
•
∂E[u]
∂t
= − {E[y · u0 (c)] − E[y] · E[u0 (c)]}
• Definition Kovarianz: Cov[X1 , X2 ] = E[(X1 − µ1 )(X2 − µ2 )] → Maßzahl für Zusammenhang zweier Zufallsgrößen
• Umformung: Cov[X1 , X2 ] = E[X1 , X2 ] − µ1 µ2
• es folgt:
∂E[u]
∂t
= −Cov[y, u0 (c)]
2
• Kovarianz von Grenznutzen und Bruttoeinkommen ist negativ, weil Grenznutzen abnehmend: Cov[y, u0 (c)] < 0
folgt, dass erwarteter Nutzen mit Steuersatz
• aufgrund des negativen Vorzeichens von ∂E[u]
∂t
steigt, das Optimum ist eine Randlösung mit t∗ = 1 und z ∗ = h
• Ergebnis: maximaler Wohlfartsstaat ist optimal, Einkommensunterschiede sollten durch
das Steuer-Transfer-System vollständig ausgeglichen werden, wenn die Bürger risikoscheu
sind und das Einkommen exogen gegeben ist
• gilt für dieses Modell (1 Periode, risikoscheue Bürger, exogenes Einkommen)
• das Einkommen wird vollständig als Steuer an den Staat abgeführt, jeder Bürger erhält
eine Sozialleistung in Höhe des Durchschnittseinkommens
• damit nimmt der Sozialstaat den Bürgern das Risiko, mit schwankendem Einkommen und
Konsumniveau konfrontiert zu werden
• der Staat sichert den Bürgern einen festen Lebensstandard zu, der seinem erwarteten
Bruttoeinkommen enstpricht
• parto-effiziente Ressourcenallokation
Frage 2b - Annahmen
• jetzt sollen Anreizwirkungen untersucht werden, deshalb wird eine Periode vorgeschaltet
• Periode 1: Individuen entscheiden, wieviel sie in Humankapital investieren wollen
• Periode 2: Konsum des Einkommens
• höhere Investition in Periode 1 → höheres erwartetes Einkommen für Periode 2
• erwarteter Lebensnutzen: U = u(c1 ) + E[u(c2 )]
• Anfangsausstattung Einkommen k in Periode 1 kann für Konsum oder Investition verwendet werden → k = c1 + h
• Einkommen Periode 2 wie Grundmodell: y = h + • Anreizwirkung: Individuen antizipieren Umverteilung in Periode 2 und bilden evtl. zu
wenig Vermögen in Periode 1
Frage 2b - ohne Umverteilung (laissez-faire)
• ohne Umverteilung sind individuelles Einkommen und individueller Konsum identisch:
c2 = y
• erwarteter Lebensnutzen: U = u(k − h) + E[u(h + )]
• U damit abhängig von Investitionsentscheidung h und exogenen Faktoren k und • jedes Individuum wählt ĥ so, dass der erwartete Lebensnutzen maximiert wird
•
∂U
∂ ĥ
= −u0 (k − ĥ) + E[u0 (ĥ + )] = 0
• u0 (k − ĥ) = E[u0 (ĥ + )]
(I)
3
• ist das ein pareto-effizienter Zustand ?
• laut Grundmodell ist eine Allokation pareto-effizient, wenn der Konsum in Periode 2
komplett abgesichert ist
• das ist gegeben, wenn jedes Individuum in Höhe des Durchschnittseinkommens der Gesamtbevölkerung konsumiert: c∗2 = h∗
• gemäß der Nutzenfunktion ist die Bewertung des Konsums in beiden Perioden gleich:
c∗1 = c∗2
• daraus folgt: c∗1 = h∗ und k = c∗1 + h∗ = 2h∗ und h∗ =
k
2
• bei pareto-effizienter Allokation wird genau die Hälfte der Anfangsausstattung in Humankapital investiert
• weil h∗ = k2 nicht gleich (I), ist die Ressourcenallokation bei fehlender Umverteilung nicht
pareto-effizient
• Ergebnis: das vollständige Fehlen von Umverteilung ist nicht optimal
Frage 2b - mit Umverteilung
• Staat beschrieben durch Steuersatz t mit und einheitliche Pro-Kopf-Zahlung z
• individueller Konsum in Periode 2: c2 = (1 − t) · (h + ) + z
• optimaler Wohlfahrtsstaat maximiert den erwarteten Lebensnutzen der Bürger unter Beachtung der Budgetbeschränkung
• Schritt 1: Wirkungsanalyse (welchen Einfluss haben t und z auf die Handlungen der
Individuen?)
• Schritt 2: Festlegung von t und z so, dass Optimum erreicht wird
• Schritt 1:
• wenn Individuum Investitionsniveau bestimmt, antizipiert es Umverteilung (Besteuerung
/ Sozialleistung)
• erwarteter Lebensnutzen: U = u(k − h) + E[u((1 − t)(h + ) + z)]
•
∂U
∂h
= −u0 (k − h) + E[(1 − t)u0 ((1 − t)(h + ) + z)] = 0
• u0 (k − h) = E[(1 − t)u0 ((1 − t)(h + ) + z)]
(II)
• Investitionsverhalten hängt implizit von t und z ab
• Anreizwirkung des Wohlfahrtsstaates vorhanden
• Staat muss bei Bestimmung der Politikvariablen Budgetbeschränkung und Anreizwirkung
beachten
• Schritt 2:
• Einsetzen von z = t · h in (II) bringt u0 (k − h) = E[u0 ((1 − t)(h + ) + t · h) · (1 − t)]
4
• Umformung: u0 (k − h) = E[u0 (h + − th − t + th) · (1 − t)] →
u0 (k − h) = E[u0 (h + (1 − t)) · (1 − t)]
(III)
• Investitionsentscheidung nun in Abhängigkeit von t
• nun: γ = 1 − t
• mit steigendem t nimmt γ ab, γ stellt somit Anreizwirkung auf t (Anreiz zur Bildung von
Humankapital) dar
• einsetzen in (III): u0 (k − h) = E[u0 (h + γ) · γ]
(IV)
• Investition in Humankapital hängt von der Anreizwirkung ab: h = f (γ)
• Staat maximiert jetzt den Lebensnutzen unter Beachtung seiner Budgetbeschränkung und
der Anreizwirkungen
• erwarteter Lebensnutzen (s.o.) mit z = t · h, ausmultiplizieren, kürzen, zusammenfassen:
U = u(k − h) + E[u(h + (1 − t))]
• mit h = f (γ) und γ = 1 − t ergibt sich: U (γ) = u(k − f (γ)) + E[u(f (γ) + γ)]
• erwarteter Lebensnutzen jetzt in Abhängigkeit von γ
• Bestimmung des optimalen Wohlfahrtsstaates: Nutzenmaximierung
•
∂U
∂γ
= −f 0 (γ) · u0 (k − f (γ)) + E[u0 (f (γ) + γ)(f 0 (γ) + )]
• einsetzen von (IV) bringt: U 0 (γ) = −f 0 (γ) · E[u0 (h + γ) · γ] + E[u0 (f (γ) + γ) · (f 0 (γ) + )]
• h = f (γ) ergibt: U 0 (γ) = −f 0 (γ) · E[u0 (f (γ) + γ) · γ] + E[u0 (f (γ) + γ) · (f 0 (γ) + )]
• zweiten E-Term teilen
• U 0 (γ) = −f 0 (γ) · E[u0 (f (γ) + γ) · γ] + E[u0 (f (γ) + γ) · f 0 (γ)] + E[u0 (f (γ) + γ) · ] (6)
• U 0 (γ) = E[u0 (f (γ) + γ)] · (1 − γ) · f 0 (γ) + E[u0 (f (γ) + γ) · ]
• ausgehend von Zustand ohne Umverteilung (t = 0, γ = 1) wird jetzt die Wirkung einer
marginalen Einführung der Staatstätigkeit beschrieben
• einsetzen von γ = 1 bringt: U 0 (1) = E[u0 (f (γ) + γ) · ]
• U 0 (1) = E[u0 (ĥ + ) · ] = Cov[u0 (ŷ), ŷ]
• wie schon gezeigt ist die Kovarianz von Grenznutzen und Bruttoeinkommen negativ
• es gilt: U 0 (1) < 0
• in einer Situation zunehmender Besteuerung sinkt Einkommen
• weil Kovarianz von Einkommen und Grenznutzen negativ, steigt der Grenznutzen bei
Besteuerung
• weil der Grenznutzen die Ableitung des erw. Lebensnutzens ist, steigt der erw. Lebensnutzen mit zunehmender Besteueuerung an
• Erklärung: Risikoaversion
5
• Bürger sind mit Wohlfahrtsstaat besser gestellt als ohne
• maximaler Wohlfahrtsstaat (t = 1) ist bei Anreizwirkung aber nicht optimal, weil Anreize
zur eignen Investition dann fehlen
• bei endogenem Einkommen ist optimale Sozialleistung geringer als Durchschnittseinkommen, die Individuen müssen einen Teil des Risikos selbst tragen
• optimaler Wohlfahrtsstaat erzeugt keine pareto-optimale Allokation, aber eine paretoVerbesserung ggü. dem Zustand ohne Umverteilung
• optimaler Steuersatz liegt zwischen 0 und 1
EXKURS: Substitutions- und Einkommenseffekt
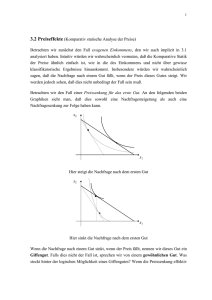
• Wie reagiert ein Konsument, der zwei Güter (x1 , x2 ) zur Auswahl hat, auf die Preisänderung
eines Gutes ?
• Vermutung: Preisanstieg führt zu Nachfragerückgang
• aber: Nachfrageanstieg bei Preisanstieg auch möglich (selbst wenn Gut normal)
• Preisänderung eines Gutes hat zwei Effekte:
1. Änderung des relativen Preisverhältnisses, zu dem man ein Gut für ein anderes
tauschen kann
2. Änderung der Kaufkraft des Einkommens
• sinkt der Preis p1 , muss man weniger von Gut 2 aufgeben, um Gut 1 zu kaufen
• zudem kann man mit gegebenem Einkommen mehr von Gut 1 kaufen, die Kaufkraft ist
gestiegen
• erster Teil: Substitutionseffekt
• zweiter Teil: Einkommenseffekt
• zur Veranschaulichung Zerlegung der Preisbewegung in zwei Schritte:
1. Änderung der relativen Preise und Anpassung (Senkung) des Einkommens, so dass
Kaufkraft konstant bleibt
2. Anpassung der Kaufkraft bei neuem relativen Preisverhältnis
• Zerlegung ist nur hypothetisch, Konsument wählt einfach neues Bündel als Reaktion auf
Preisänderung
• Hinweis: Substitutionseffekt immer entgegen der Preisänderung
(Preis ↓, Nachfrage ↑)
• Hinweis: Einkommenseffekt nicht immer entgegen der Preisänderung:
normales Gut (Preis ↓, Nachfrage ↑) vs. inferiores Gut (Preis ↓, Nachfrage ↓)
• Bsp.: Mais, Arbeit
• wie der Gesamteffekt ausfällt, ist unklar, er kann bei sinkendem Preis positiv und negativ
sein
6
• in der Summe ist ausschlaggebend, ob der Einkommenseffekt den Substitutionseffekt
überwiegt oder nicht
• das ist die Aufteilung nach Slutsky (Slutsky-Gleichung)
• andere Möglichkeit: Hicks-Gleichung
• Hicks hält bei neuem Preisniveau nicht die Kaufkraft, sondern den Nutzen konstant
• Substitutionseffekt nach Hicks: konstantes Nutzenniveau bei neuem relativen Preisverhältnis
• sinkt Preis p1 , wird Einkommen entzogen bis sich das Individuum das alte Nutzenniveau
gerade wieder leisten kann
• Einkommenseffekt: bei neuem Preisniveau wird Einkommensentzug rückgängig gemacht
• Hicks-Substitutionseffekt auch entgegen der Preisänderung
• Grafik 2 (Varian, S. 180)
Frage 3 - Annahmen
• repräsentativer Haushalt, dessen Nuten U sich aus dem Konsum eines Güterbündels x
und der ihm zur Verfügung stehenden Freizeit ergibt: U (x, F )
• maximal steht ihm die Zeit F̄ zur Verfügung
• das Arbeitsangebot (Arbeitszeit) ergibt sich dann aus F̄ − F
• die Arbeit wird mit dem Lohnsatz w vergütet
• das Arbeitseinkommen beträgt damit (F̄ − F )w
• dieses Arbeitseinkommen wird mit dem proportionalen Steuersatz t besteuert
• das verbleibende Nettoeinkommen (F̄ − F )w(1 − t) wird vollständig für den Konsum des
Güterbündels x zum Preis p ausgegeben (es wird nicht gespart)
Frage 3 - Proportionale Steuer
• repr. Haushalt maximiert seinen Nutzen max U (x, F ) unter Beachtung der Budgetbeschränkung (F̄ − F )w(1 − t) = px
• F̄ w(1 − t) − F w(1 − t) = px
• Dividieren durch p ergibt F̄ wp (1 − t) = x + F wp (1 − t)
• linke Seite: maximal mögliches reales Nettoeinkommen (keine Freizeit) → Verwendung
für Konsum oder Freizeit (bewertet zum realen Nettolohn)
• hat sich Konsument für bestimmten Umfang an Freizeit entschieden, stehen Arbeitsangebot und Konsum zu gegebenen Preisen fest
• Bedingung im Nutzenmaximum: M RSF,x =
δU/δF
δU/δx
=
w(1−t)
p
• MRS = Verhältnis, zu dem ein Gut gegen ein anderes getauscht wird
• Was ist der Preis einer Einheit Freizeit ? - Nettolohn entgangener Arbeit
7
• Was ist der Preis einer Einheit x ? - Preis p
• im Optimum ist MRS zwischen Freizeit und Konsum gerade dem Preisverhältnis aus
Nettolohnsatz und Preis des Güterbündels
• Grafik 3 (Wellisch, S. 94)
• ohne Einkommensteuer: Budgetgerade läuft von F̄ nach F̄ wp
• maximaler Nutzen in A
• hier: Steigung der Indifferenzkurve (Grenzrate der Substitution zwischen Freizeit und
Konsum) gleich Steigung der Budgetgerade (Opportunitätskosten der Freizeit)
• Arbeitsangebot ist dann (F̄ − F1 )
• jetzt: proportionale Einkommensteuer wird eingeführt → Budgetgerade dreht sich um F̄
nach innen
• Konsum des Güterbündels x wird teurer, Haushalt erhält für Verzicht auf Einheit Freizeit
weniger x als ohne Besteuerung, Haushalt muss mehr Freizeit opfern, um alte Menge x
zu erhalten
• Haushalt wählt Freizeit-Güter-Kombination B
• in unserem Bsp. verringert sich das Arbeitsangebot von (F̄ − F1 ) auf (F̄ − F2 )
• Argumentation: Freizeit wird relativ billiger, x wird durch F ersetzt, Nachfrage nach
Freizeit steigt, Nachfrage nach x sinkt, Arbeitsangebot sinkt
• unter anderen plausiblen Präferenzstrukturen auch andere Reaktion denkbar
• genauerer Einblick: Zerlegung des Gesamteffektes in Substitutions- und Einkommenseffekt
• Substitutionseffekt: Einführung der Besteuerung reduziert Opportunitätskosten der Freizeit von w auf w(1 − t)
• würde der Haushalt soviel Einkommen erhalten, dass er auch nach Einführung der Steuer
den Nutzen U 1 halten könnte, würde seine Nachfrage nach nun relativ billiger gewordener
Freizeit eindeutig zunehmen
• weil Güterbündel relativ teurer und Freizeit relativ billiger geworden ist, wird Konsum
durch Freizeit ersetzt
• geringerer Relativpreis der Freizeit führt zu Anstieg des Freizeitkonsums (Substitutionseffekt immer entgegen Preisänderung)
• Substitutionseffekt führt also immer zu einem Rückgang des Arbeitsangebotes bei Besteuerung (A → C)
• Wie kann erhöhte Freizeitnachfrage aussehen ? - keine Überstunden, geringere Arbeitsproduktivität, frühzeitige Pensionierung, Verringerung der täglichen / monatlichen Arbeitszeit
• allerdings verringert die proportionale Lohnsteuer auch das Realeinkommen
8
• im Substitutionseffekt wurde dem Haushalt soviel Einkommen gegeben, dass er sein altes
Nutzenniveau halten kann
• das wird jetzt rückgängig gemacht
• Einkommenseffekt (C → B) ist eine Änderung des Einkommens bei neuem relativen
Preisverhältnis
• hier: es wird bei konstanten Preisen (d.h. konstanter Budgetgerade) soviel Einkommen
entzogen, wie ihm vorher dazugegeben wurde
• Haushalt erreicht jetzt geringeres Nutzenniveau Ū2
• ist Freizeit ein normales Gut, ist der Einkommenseffekt dem Substitutionseffekt entgegengesetzt
• Nachfrage nach Freizeit wird teilweise rückgängig gemacht
• hier: in der Summe bleibt ein Nachfrageanstieg nach Freizeit
Frage 4 - (Un)Gebundene Tansfers
• um pareto-effiziente Allokation zu erreichen, müsste direkt an der Leistungsfähigkeit angesetzt werden
• Unterstützung bei unterdurchschnittlicher Leistungsfähigkeit u.u.
• Leistungsfähigkeit lässt sich aber in der Praxis nicht ausreichend gut fassen
• deshalb wird auf andere Größen ausgewichen, z.B. Einkommen
• Zusammenhang: wer hohes Einkommen erzielt, ist leistungsfähig (bestreitbar)
• Transfers, die an solchen Hilfsgrößen angreifen, nennt man gebundene Transfer
• Bsp.: Wohngeld, Mietkosten sinken
• Vergleich mit freiem Transfer
• Individuum erhält eine Geldleistung, ungebundener Transfer
• Individuum kann jetzt zwar auch das Konsumbündel zusammenstellen, dass es mit gebundenem Transfer erhalten hätte (Finanzierung Mietkosten)
• es erhält aber auch weitere Konsummöglichkeiten, kann die Unterstützung anderweitig
verwenden
• Grafik 4 (Corneo, S. 170)
• Individuum konsumiert zwei Güter und erreicht U0 und Punkt A
• Preis Gut 1 = 1 (Numéraire)
• Gut 2 wird nun subventioniert zum Satz von σ pro konsumierter Einheit
• Budgetbeschränkung x1 + (p2 − σ)x = y
• durch Subvention verbilligt sich Gut 2 relativ zu Gut 1
9
• Drehung der Budgetgerade in y
• Individuum erreicht Güterbündel B und höheren Nutzen Û
• Gibt der Staat einen freien Transfer in Höhe von s Einheiten des Numéraire-Gutes, verschiebt sich die Budgetgerade nach außen
• Individuum kann sich weiterhin Güterbündel B leisten
• es kann aber auch ein anderes, höheres Nutzenniveau U ∗ und Güterbündel D erreichen
• Ergebnis: der gleiche Subventionsbetrag führt bei einem freien Transfer zu einem höheren
Nutzenniveau des Empfängers
• anders: der Staat könnte durch freien Transfer die gleiche Nutzensteigerung ermöglichen,
hätte aber geringere Ausgaben, wie bei gebundenem Transfer
• diese nicht wahrgenommene Ersparnis öffentlicher Ausgaben ist die Zusatzlast des gebundenen Transfers
Frage 5 - Wohlfahrtssicherung
• Armutsbekämpfung: jeder Bürger muss einen Nutzen erreichen, der über einem exogen
festgelegtem Niveau Ū liegt
• Aufgabe des Staates: Verhinderung der Armut mit minimalen Ausgaben
• Annahme: Staat hat vollständige Information, kennt Produktivität und Markteinkommen
des Hilfebedürftigen
• Staat unterstützt dann nur die Individuen, die durch eigne Leistungsfähigkeit nicht in der
Lage sind, Ū zu erreichen
• bei diesen Individuen wird Ū mit geringsten Ausgaben erreicht, wenn der Staat ihnen eine
Pauschalsubvention zahlt und ihnen die Arbeit-Freizeit-Entscheidung selbst überlässt
• mit der Transferzahlung zi erreicht das Individuum i dann genau Ū
• Annahmen:
• Individuen haben identische Präferenzen
• sie unterscheiden sich aber hinsichtlich ihrer Produktivität, d.h. Lohn wi / Stunde
• Markteinkommen ist dann yi = wi · li
• jedes Individuum hat eine Einheit Zeit, die für Arbeit l oder Freizeit f ausgegeben werden
kann
• ihre Arbeitszeit ist l = 1 − f
• Grafik 5 (Corneo, S. 216)
• ohne Unterstützung erreicht das Individuum Punkt L als Schnittpunkt der Budgetgerade
mit der Nutzenfunktion ohne Umverteilung V (wi , 0)
• die Freizeit ergibt sich aus 1 − l(wi , 0)
10
• ist dieses Nutzenniveau kleiner Ū , erhält das Individuum eine Pauschalsubvention, die Ū
sicherstellt
• Pauschalsubvention: Budgetgerade verschiebt sich nach außen
• mit der neuen Budgetgerade kann auf Ū der Punkt S realisiert werden
• die Freizeit beträgt jetzt 1 − l(wi , zi∗ )
• die Grafik zeigt, dass es keine billigere Methode gibt, das Individuum auf Ū zu bringen
• unter allen Punkten auf Ū ist S der mit dem kürzesten vertikalen Abstand zur individuellen Budgetgerade
• dieser Abstand entspricht der Höhe des Transfers
• dabei geht das Arbeitsangebot des Hilfeempfängers zurück
Frage 6 - Einkommenssicherung
• normalerweise wird Armutsbekämpfung nicht als Sicherung eines minimalen Nutzenniveaus verstanden
• sondern als Sicherung eines minimalen Konsumniveaus
• Aufgabe des Staates: Einkommenssicherung bei minimalen Ausgaben
• Armutsbekämpfung: jeder Bürger muss mindestens ein exogen festgelegtes Existenzminimum x̄ erreichen
• als Konsequenz existiert ein kritischer Lohnsatz ŵ
• Individuen mit einem Lohnsatz niedriger als ŵ verdienen ohne Umverteilung weniger als
das Mindesteinkommen x̄
• Individuen mit einem höheren Lohnsatz als ŵ verdienen mehr als für x̄ nötig ist
• damit Hilfeempfänger x̄ mit minimalen öffentlichen Ausgaben erreichen, sollen sie möglichst
viel Einkommen selbst erzielen
• Transferzahlung ist dann individuelles Markteinkommen minus Existenzminimum
• das vom Individuum selbst beigesteuerte Arbeitspensum ist l¯i
• das Individuum verpflichtet sich, l¯i Stunden einer Tätigkeit nachzugehen und erhält einen
Transfer, der x̄ sichert
• Grafik 6 (Corneo, S. 218)
• Punkt L ist erreichbares Güterbündel ohne Unterstützung
• damit wird x̄ aber nicht gesichert
• das Individuum erhält eine Unterstützung, die auf gleichem Nutzenniveau liegt (Punkt
S)
• Punkt S wird erreicht, indem das Individuum eine Eigenleistung erbringt
11
• im Punkt S konsumiert das Individuum mehr und es arbeitet mehr
• Ergebnis: unter vollständiger Information verursacht eine optimale Einkommenssicherung
eine Zunahme des Arbeitsangebotes bei konstantem Nutzen
12