Starrer Koerper - Physik (Uni Würzburg)

5 Mechanik starrer Körper
Warum gibt es Atome ?
5.1 „Starre Körper“
Viele Massenpunkte, deren Relativkoordinaten zeitlich konstant sind.
Bei hinreichend großer Zahl von Massenpunkten betrachtet man das
Objekt als „starren Körper“ mit kontinuierlicher Massenverteilung.
Durch die Festlegung der Relativkoordinaten werden die Freiheitsgrade
des starren Körpers auf 6 reduziert:
3 Komponenten der Schwerpunktsgeschwindigkeit
3 Komponenten des Drehimpulses
Bewegungen starrer Körper werden zerlegt in
Translation und Rotation.
1
5.1 Schwerpunkt
Schwerpunkt
r
ri
n
Erinnerung:
r
rS =
∑m
i
i =1
n
∑m
massengewichtete
Durchschnittskoordinate
i
i =1
Übergang zu kontinuierlicher Massenverteilung
dM
dV
Massendichte
ρ=
Gesamtmasse
r
M = ∫ ρ (r ) dV
K
Schwerpunktsvektor
r
r
r
rS = ∫ dM
M
K
Für die Translation des Schwerpunktes gelten
die bisher gelernten Gesetze.
5.1 Schwerpunktsbewegung
Der Schwerpunktsbewegung kann noch eine Rotation überlagert sein,
wobei jedoch nur Drehachsen durch den Schwerpunkt möglich sind.
Der Schwerpunkt bewegt sich
auf einer Parabel (schiefer Wurf)
Gleichzeitig wird eine Drehung
ausgeführt
Hochsprung
Schwerpunkt bleibt
unter der Latte
2
5.2 Trägheitsmoment und Rotationsenergie
Trägheitsmoment eines Massenpunktes
Ursprung in
Bewegungsebene !
J = mr 2
Dies gilt für starren Körper nicht mehr !
Drehachse
Verallgemeinerung für starren Körper:
dM
(= EkindM ) = 12 dM v 2 = 12 dM ωr × rr 2
E rot
r r
r r
r
ω
r
dM
R = r sin α
α
ω × r = ω r sin α = ω R
r
r
dM
E rot
= 12 dM ω 2 R 2
Rotationsenergie
E rot =
Trägheitsmoment
1 2 2 r
1
ω ∫ R ρ (r ) dV = J ω 2
2
2
K 4243
1
=J
r
J = ∫ ρ(r ) R 2 dV
K
5.2 Versuch: Fallmaschine
Potentielle Energie des Gewichtes
→ Rotationsenergie des Balkens
Drehbalken
Geschwindigkeitsmessung
mit Lichtschranke
Gewicht
100 g
3
5.2 Versuchsauswertung
2
J = J Balken + ∑ mi Ri
1
2
2
J 1 ω1 = m g h
2
1
2
J 2 ω2 = m g h
2
i =1
J1 < J 2
mi
mi
ω1 > ω2
m
m
m g h = 0.1 kg ⋅ 9.81 m s −2 ⋅ 0.2 m = 0.196 J
r r
0.05m
0.166
v ∆s
=
v LS = ω × r = ω R ⇒ ω = = Balken =
R R ∆t LS 0.3m ∆t LS
∆t LS
5.2 Trägheitsmoment eines Zylinders
Gesamtmasse:
M = ρ π Rmax h
2
Zylinderachse = Drehachse
dV
Trägheitsmoment:
R
J = ∫ ρ R 2 2 π R h dR
1424
3
V
dV
Rmax
= 2π ρ h
∫R
3
dR
0
4
= 12 π ρ h Rmax
2
= 12 M Rmax
4
5.2 Trägheitsmoment einer Kugel
J Kugel =
∫R
2
ρ dV
Kugel
R π 2π
= ρ ∫ ∫ ∫ r 2 sin 2ϑ r 2 sinϑ dϕ dϑ dr
1
424
3 1442443
0 0 0
R2
dV =da db dr
Rπ
= 2π ρ ∫ ∫ r 4 sin 3ϑ dϑ dr
0 0
Rπ
= 2π ρ ∫ ∫ r 4 sin 3ϑ dϑ dr
0 0
R
R
= 2π ρ
4 4
r dr
3 ∫0
= 2π ρ
4 R5 2
= M R2
3 5 5
5.2 Rollen auf der schiefen Ebene
1
1
Ekin = m v 2 + J ω 2
2
2
1
1
= m r 2ω 2 + J ω 2
2
2
v = rω
Ekin = ∆ E pot
1
1
m r 2ω 2 + J ω 2 = m g ∆h
2
2
Endgeschwindigkeit ist bei gleicher
2 m g ∆h
Masse und Abrollradius nur vom
v=r
Trägheitsmoment abhängig
m r2 + J
5
5.2 Steinerscher Satz
Ist das Trägheitsmoment bezüglich einer Achse durch den Schwerpunkt
bekannt, ergibt sich für eine andere dazu parallele Achse:
J = ∑ mi Ri
2
i
r r 2
= ∑ mi a + Ri′
r
a
andere
Achse
i
r r
2
= ∑ mi (a 2 + 2 a ⋅ Ri′ + Ri′ )
r
Ri
r
R′i
Achse durch
Schwerpunkt
i
r
r
2
= ∑ mi Ri′ + 2a ∑ mi Ri′ + a 2 ∑ mi
i
i
14i243
=0
Das Trägheitsmoment bezüglich der neuen Achse:
J = J S + M a2
a : Abstand der Achse vom Schwerpunkt
5.3 Drehmoment
r r
E rot = 12 J ω 2 = 12 J ω ⋅ ω
Rotationsenergie
r r r r
r r
dE rot 1
= 2 J (ω& ⋅ ω + ω ⋅ ω& ) = J ω& ⋅ ω
dt
r
dE rot
r& dϕ
= J ω⋅
dt
dt
r r
dE rot = J ω& ⋅ dϕ
r
r
E rot = ∫ {
J ω& ⋅ dϕ
r
=: M
analog zu:
r r
Ekin = ∫ m
v& ⋅ ds
{
r
F
Drehmoment:
r
r
M = J ω&
Aktionsprinzip, analog zu:
r
r
r
F = mv& = m a
6
5.3 Drehmoment und Kraft
r
r
Rotationsenergie E rot = ∫ M ⋅ dϕ
r r
somit gilt: dE = M ⋅ dϕ
r r
Außerdem gilt dE = F ⋅ ds
mit
r r
r
d s = dϕ × r
Achse
r
M
r
dϕ
r
ds
r dϕ
r
r
r r
dE = F ⋅ (dϕ × r )
erhält man
r
F
Kreuzprodukt! Es gilt folglich ebenso:
r
r r
dE = r × F ⋅ dϕ
(
)
Somit:
r r r
M = r ×F
5.3 Gleichgewicht
indifferent
stabil
Ein statisches Gleichgewicht ist immer dann
vorhanden, wenn ein Körper über längere
Zeit seine Lage und seine Form beibehält.
Dazu müssen folgende zwei
Beziehungen erfüllt sein:
1. Die Summe der Kräfte muss verschwinden
r
r
r
F1 + F2 + ... + Fn =
n
r
∑F
i
= 0
i =1
labil
2. Die Summe der Momente muss
verschwinden
r
r
r
M 1 + M 2 + ... + M n =
r
M
∑ i =0
n
i =1
→ Hebelgesetze
7
5.4 Drehimpuls eines starren Körpers
r
Drehimpuls L einer Punktmasse
r r r
L=r×p
r
L = 1 kg m 2 s −1 = 1 J s
[]
Drehimpuls eines starren Körpers
r
r r r
L = ∫ r × v (r ) dM
V
r r r
= ∫ r × (ω × r ) dM
1442r44
3
V
= dL
r
r r r
= ∫ (r 2 ⋅ ω − (ω ⋅ r ) ⋅ r )dM
V
Drehimpuls
→
→
L im allgemeinen nicht parallel zu ω !
5.4 Berechnung des Drehimpuls
Drehimpuls Masse
m1
Spiegelsymmetrische
Masse m2=m1
Gesamtdrehimpuls ist
→
parallel zu ω.
r
rr
r r r
L1 = m1r1 × (ω × r1 ) cos ∠ω L1
rr
rr
= ω m1 r12 sin(∠ω r1 )cos ∠ω L1
rr
= ω m1 r12 sin 2 (∠ω r1 )
(
Für Körper die spiegelsymmetrisch
zu einer Ebene in der die→ Drehachse
liegt ist der Drehimpuls L parallel zur
Winkelgeschwindigkeit
→
ω.
(
)
)
= ω m1 R12
Gesamtdrehimpuls für symmetrischen Körper
r
L = ω ∫ ρ (r ) R 2 dV = ω J
V
8
5.4 Drehimpuls und Drehmoment
Für Punktmasse auf Kreisbahn gilt:
r
r
r
dL  d r r   r d p  r r
r r r r r
=
× p +  r ×
 = (v × p ) + r × F = r × F = M
dt  dt
dt 
 
(
)
Für rotierenden starren Körper:
1
J ω2
2
r
r r&
r& dϕ
dErot 1 d 2
= J (ω ) = J ω ω = J ω
dt
2 dt
dt
r& r
dE = J ω dϕ
E rot =
rot
Rotationsenergie
Kettenregel, Vektoren !
·dt
r r
E rot = ∫ {
J ω& dϕ
r
∫
M
r& r
Bewegungsgleichung für Drehimpuls
L=M
5.4 Drehimpulserhaltung
Analog zu der Schreibweise des Newtonschen Aktionsprinzips der
Translation:
r
r d pr
dv dm r
F=
=m
+
v
dt
dt dt
ergibt sich für Rotation um feste Achse:
r
r
r dL
dω d J r
=J
+
M=
ω
dt
dt dt
Wenn kein äußeres Drehmoment wirkt, bleibt der Drehimpuls
erhalten:
Drehimpulserhaltungssatz
r
r
dL r
= M = 0 ⇒ L = const.
dt
9
5.6 Drehimpuls eines starren Körpers
r
r r r
L = ∫ r × v (r ) dM
V
r r r
= ∫ r × (ω × r ) dM
1442r44
3
V
= dL
r r r r
= ∫ (r 2 ⋅ ω − (ω ⋅ r ) ⋅ r )dM
V
r
r r r
= ∫ r 2 ⋅ ω dM − ∫ (ω ⋅ r ) ⋅ r dM
V
V
Vektorgleichung in Komponenten zerlegen
3 

Li = ∑  δ ij ∫ r 2 dM − ∫ ri r j dM  ω j
j =1 
V
V
14
44424
444
3
J ij
Definition: Trägheitstensor
mit
1 i = j
0 i ≠ j
δ ij := 
J ij = ∫ (δ ij r 2 − ri rj )dM
V
5.6 NR: Trägheitstensor
r r
Li = ωi ∫ r 2 dM − ∫ (ω ⋅ r ) ⋅ ri dM
V
V
3
= ωi ∫ r 2 dM − ∫ ri ∑ ω j r j dM
V
j =1
V
3
= ωi ∫ r 2 dM − ∑ ω j ∫ ri rj dM
V
j =1
V


= ∑  δ ij ∫ r 2 dM − ∫ ri r j dM  ω j
j =1 
V
V
14
44424
444
3
J ij
3
J 12 J 13   ω1 
J
r  11
 
r
L =  J 21 J 22 J 23   ω2  = Jˆ ω
J
J 32 J 33   ω3 
31
14
42
443
Jˆ
mit
1 i = j
0 i ≠ j
δ ij := 
Trägheitstensor verknüpft
Drehachse und Drehimpuls
10
5.6 Beispiel: Trägheitstensor eines Quaders
J ij = ∫ δ ij r 2 − ri rj dM
14243
V
jij
 y2 + z2

ˆj =  − y x
 −zx

c b a
2 2 2
J 11 =
∫ ∫ ∫ (y
c b a
− − −
2 2 2
2
− xz 

− yz 
x 2 + y 2 
−xy
x2 + z2
−zy
 b2 c 2 
 b2 c 2 
2


)
z
dx
dy
dz
a
b
c
M
ρ
ρ  +  =  + 
+
=
 12 12 
 12 12 
 b2 + c 2
M
Jˆ =  0
12 
 0
Trägheitstensor eines
Quaders mit
homogener Dichte
0
a + c2
0
2
0 

0 
a 2 + b 2 
5.6 Drehung eines Quaders um Raumdiagonale
a = 2m, b = 3m, c = 1m, M = 2kg
 b2 + c 2
M
Jˆ =
 0
12 
 0
0
a +c
0
2
 2
 
ω =  3  rad s −1
1
 
r

10 0 0 
 2

0  =  0 5 0  kg m 2
12 

a 2 + b 2 
 0 0 13 
0
2
10 0 0   2 
 20 
r 1
 
1 
L =  0 5 0   3  Js =  15  J s
12  
12 
 
 0 0 13  1 
 13 
Drehimpuls ist nicht parallel zu Drehachse
z
→
L
x
ω→
y
Drehimpuls bewegt sich auf einem Kegel
11
5.6 Trägheitsellipsoid
r
r
L = Jˆ ω
Trägheitstensor erlaubt nun die Berechnung des
Drehimpulses für jede Drehachse durch den Schwerpunkt
Trägt man
1
J
r
L
J= r
für jede mögliche Achse durch den
Schwerpunkt auf, erhält man einen Ellipsoid.
ω
Beispiel: Quader
Das Ellipsoid hat drei
Hauptachsen (die senkrecht
zueinander stehen).
Die Trägheitsmomente in
diesen Richtungen nennt man
„Hauptträgheitsmomente“.
5.6 Hauptträgheitsmomente
Mit einem kartesischen Koordinatensystem
entlang der Hauptachsen ist der
Trägheitstensor diagonal
 Ja

ˆ
J = 0
0

0
Jb
0
0

0
J c 
Ja, Jb und Jc sind die Hauptträgheitsmomente.
Oblates Trägheitsellipsoid
Prolates Trägheitsellipsoid
Ein großes und zwei kleine
Zwei große und ein kleines
Hauptträgheitsmomente
Hauptträgheitsmoment
12
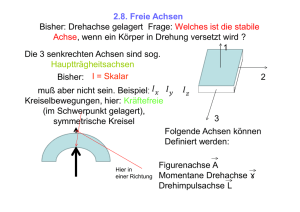
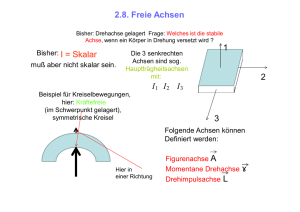
5.6 Freie Achsen
Die eingezeichnete Drehachse kann nur durch
Kräfte auf die Achse beibehalten werden, denn
m1
r
r
dL
≠0
dt
ω
r
L
Nach Freigabe der Achse
r erfolgt die Drehung
um die Richtung von
r
dL
=0
dt
Achse
L
m2
Kräfte wirken nur noch entlang der
kräftefreie
Achse
Stange (innere Radialkräfte).
r
L
r
m1
ω
Auf die Achse wirkt kein Drehmoment.
Solche Achsen bezeichnet man als
m2
„freie Achsen“
5.6 Freie Achsen und Hauptträgheitsmomente
Achsen in Richtung der Hauptachsen des Trägheitsellipsoids sind
freie Achsen.
Der Vektor
damit folgt
r
ω
hat nur eine Komponente, z.B
 La   J a
  
 Lb  =  0
L   0
 c 
0
Jb
0
r
ω = (0,0, ωc )
 0
  
⋅ 0 
J c   ωc 
0
0
r
L = (0,0, J cω c )
r r
und somit ω || L .
oder
Also ist die Achse kräftefrei.
13
5.6 Stabilität Freier Achsen
Rotationen um die Achse mit dem größten und mit dem kleinsten
Trägheitsmoment sind stabil.
Rotation um die Achse mit dem mittleren Trägheitsmoment ist nicht
stabil.
(kleine Störungen führen zum Torkeln).
5.7 Kreisel
Definition:
Ein Kreisel ist ein an einem Punkt
P festgehaltener
rotierender starrer Körper
Die Bewegung des Kreisels ist bestimmt durch
seine Massenverteilung (Trägheitstensor)
die Art und Lage des Unterstützungspunktes
P
(d.h. durch die auf den Kreisel wirkenden Kräfte )
Daher werden unterschieden:
symmetrischer und unsymmetrischer Kreisel
kraftfreier und schwerer Kreisel
unsymmetrischer Kreisel: 3 unterschiedliche Hauptträgheitsmomente
symmetrischer Kreisel: mindestens 2 gleiche Hauptträgheitsmomente
14
5.7 Versuch: Kugelkreisel
Bewegungsformen mit angeschraubter Achse (schwerer Kreisel):
- langsame Drehung der Drehachse um vertikale Mittelachse
- überlagerte schnelle Kreisbewegung der Drehachse nach „Stoß“
Bewegungsformen ohne Achse (kräftefreier Kreisel):
- Drehachse der Kugel bleibt in Ruhe
- schnelle Kreisbewegung der Drehachse nach „Stoß“
5.7 Kräftefreier symmetrischer Kreisel
symmetrischer Kreisel: o.B.d.A.
Ja = Jb ≠ Jc →
Figurenachse
c
kräftefreier Kreisel:
zwei Beispiele zur kräftefreien Lagerung eines Kreisels
reibungsfreie direkte Unterstützung
des Schwerpunktes
→
Kreisel nach Rozé, „Kleinscher Kreisel“
reibungsfreie und frei bewegliche
Unterstützung der Figurenachse in zwei
Punkten die Kräfte (z.B. Schwerkraft) auf
Kreisel genau ausgleicht
→
Gyroskop
15
5.7 Nutation des symmetrischen Kreisels
r r
Ausgangszustand: L ω Figurenachse
Schwerpunkt
Durch kurze äußere Einwirkung wird ein
Drehimpuls um eine beliebige Achse
übertragen
Figurenachse
c
Lc = J cωc
Richtungen von Drehimpuls,
r
ω
momentaner Winkelgeschwindigkeit
r
L
und Figurenachse sind verschieden
Nach Drehimpulserhaltung ist neuer
La = J aωa
Drehimpuls raumfest
a
5.7 Nutation
Die Richtung der Figurenachse kreist um die Drehimpulsrichtung
→ Nutation (Figurenachse bewegt sich auf dem Nutationskegel)
Die Richtung der momentanen Drehachse kreist um die
Drehimpulsrichtung (Rastpolkegel)
Figurenachse
c
r
ω
r
L
Nutationskegel
Rastpolkegel
a
Die Bewegung ist notwendig, um Drehimpuls und Energie zu erhalten.
16
5.7 Präzession
Ein Kreisel, auf den äußere Drehmomente (Kräfte) wirken, präzediert.
Insbesondere meint man Drehmomente auf die Figurenachse, die die
Richtung, aber nicht den Betrag des Drehimpulses ändern.
r
L
Bewegung des
Drehimpulses
gemäß
Schwerpunkt
r
dL r
=M
dt
Gewicht
r
FG
r
r
r r
L + M dt
r
M
r r
M ⊥L
5.7 Präzessionsfrequenz eines sym. Kreisels
r
r
L (t )
In der Zeitspanne dt hat sich L
um
dα gedreht, daraus ergibt sich
die Präzessionsfrequenz:
ωP =
Mit
dα =
dL
L
dα
dt
wird:
dα
r
L (t + dt )
r
dL
1 dL
L dt
M
ωP =
L
M
ωP =
Jω
ωP = ⋅
17
5.8 Zusammenfassung Kapitel 5
5 Mechanik starrer Körper
6.1 „Starre Körper“
6.2 Trägheitsmoment und Rotationsenergie
6.3 Drehmoment
6.4 Drehimpuls eines starren Körpers
6.5 Anwendungen
6.6 Drehimpuls eines starren Körpers
6.7 Kreisel
5.8 Literatur
Kreisel
David Himmel,
„Theorie und Experimente zum mechanischen Kreisel als Grundlage
eines Versuchs im Anfängerpraktikum“ Zulassungsarbeit
Zulassungsarbeit, 1998, Köln
http://www.paehler.org/tim/archiv/extern/david/
Der Stehaufkreisel
http://www.physik.uni-augsburg.de/~wobsta/tippetop/index.shtml.de
Der Büroklammerkreisel – Sakai-Kreisel
Christian Ucke, „Kreisel aus Büroklammern“
Physikalische Blätter 54 (1998), 440-442
18