1 Die Normalverteilung (Gauß-Verteilung) Letzte Änderung 14. Juni

1
Die Normalverteilung (Gauß-Verteilung) Letzte Änderung 14. Juni 2000, 27 Seiten
1 Definition der Normalverteilung
Eine Zufallsvariable mit der Dichte
f: R→R
f(x) =
1
2πσ 2
e-
(x-µ)2
2σ2
heißt normalverteilt mit Parametern µ∈R, σ2∈R++.
Eine verbreitete Kurzschreibweise für diese Universalverteilung der Normalverteilung ist
N(µ,σ2) oder N(µ,σ 2) oder N(µ,σ).
Ob σ2 oder σ als zweites Argument verwandt wird, ist im Regelfall aus dem Zusammenhang klar. Die Verteilung für die (0,1) Variable, d.h. N(0,1), die StandardNormalverteilung wird wie folgt bezeichnet (die Abkürzung der Normalverteilung):
Φ(x) =
x
f(u) du
-∞
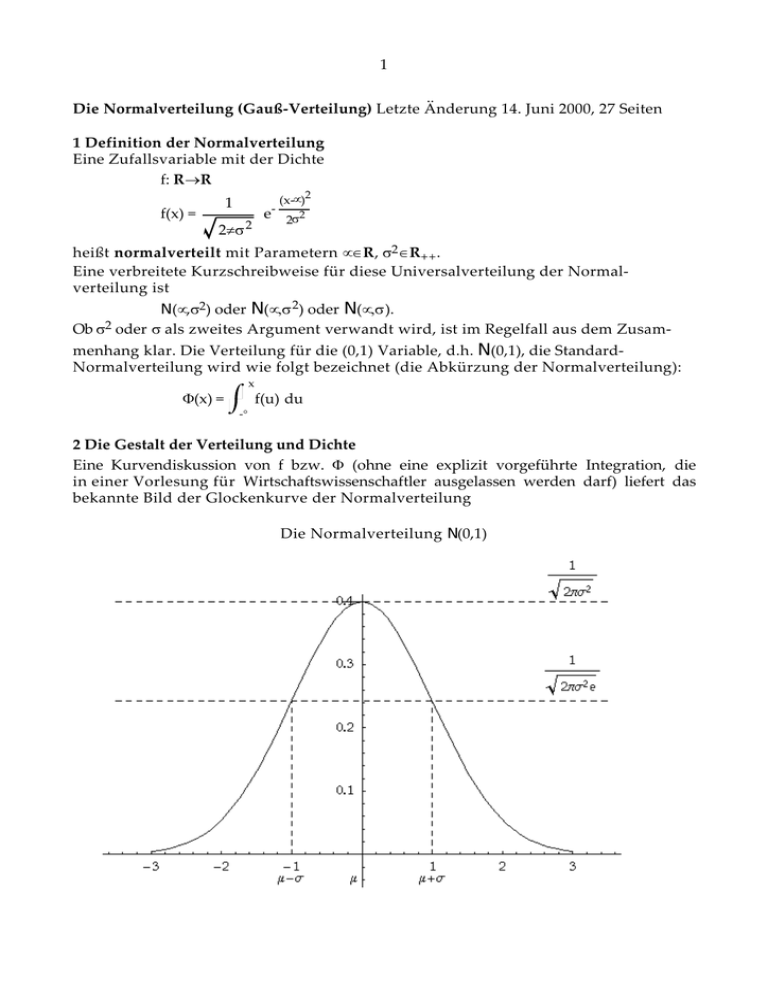
2 Die Gestalt der Verteilung und Dichte
Eine Kurvendiskussion von f bzw. Φ (ohne eine explizit vorgeführte Integration, die
in einer Vorlesung für Wirtschaftswissenschaftler ausgelassen werden darf) liefert das
bekannte Bild der Glockenkurve der Normalverteilung
Die Normalverteilung N(0,1)
2
Eine Kurvendiskussion von f(x) liefert sofort:
1. Symmetrie
f ist symmetrisch um den Extremwert µ, d.h. f'(µ)= 0.
2. Monotonie
f ist streng monoton steigend von -∞ bis µ, und streng monoton fallend
von µ bis +∞.
3. Konkavität/Konvexität
f hat zwei Wendepunkte in µ ± σ
4. Aus der Symmetrie von f um µ folgt die für Φ, d.h. 1 - Φ(µ - x) = Φ(µ + x)
Damit ist f, eine stetige Funktion, vollständig beschrieben. Üblicherweise bezeichnet
man sie als Glockenkurve der Normalverteilung.
Die numerischen Werte sind aus den Tafeln auf den Seiten 26-28 zu entnehmen.
Für die Verteilung gibt es keinen geschlossenen Ausdruck, d.h. es existiert keine
Stammfunktion F(x). Aber die entsprechenden Werte der Fläche unter obiger Kurve
können numerisch gefunden werden. Deswegen ist eine Tabelle der einzige Weg, F(x)
schnell verfügbar zu haben; sie wird üblicherweise mit Φ(x) bezeichnet.
Ohne Beweis sei darauf hingewiesen, daß
(1)
E(X) = µ
(2)
var(X) = σ2 .
M.a.W. die in der Spezifikation der Normaldichte auftretenden Parameter sind
Erwartungswert und Varianz.
3
3 Variationen
Die Vielfalt der Normalverteilung läßt sich schnell durch eine Folge von ParameterVariationen zeigen
1. Zur Vielfalt der Normalverteilungen: die Variation der Varianz
Die Dichten und Verteilungen zu N(0, 1), N(0, 1.69), N(0, 3.21)
Ein gutes Maß für die Lage der Verteilung wird durch die Antwort zu der Frage:
"Wie sehen die Dezile aus?" gegeben:
Die Dezile für N(0,1):
für N(0,1.69
für N(0,3.21)
-1.28155
-2.16582
-4.11378
-0.841621
-1.42234
-2.7016
-0.524401
-0.886237
-1.68333
-0.253347
-0.428157
-0.813244
0 = Median = Mittelwert
0.253347
0.428157
0.813244
0.524401
0.886237
1.68333
0.841621
1.42234
2.7016
1.28155
2.16582
4.11378
(Dezil k liefert die Wahrscheinlichkeit P[X ≤ dk ] = k.0.1, k=1, 2, …,9, 10)
4
2. Der Grenzfall einer nicht-zufälligen Größe: die Variation der Varianz → 0
Für eine monoton sinkende Varianz schrumpft die Zufallsgröße X zu einer
Konstanten, ein Grenzübergang, der später als Konsistenz bezeichnet wird (s.u.
Statistik II). Die bildliche Darstellung der Normalverteilung mit σ2 → 0, ist eine
Glockenkurve, die immer nadelförmiger um µ herum wird:
Die hier benutzten Varianzen, die das Phänomen bereits deutlich zeigen, sind
σ2 = 1.72, 1.32, 1.0, 0.72, 0.42
bei gemeinsamen Mittelwert µ = 0
5
3. Zur Vielfalt der Normalverteilungen: die Variation des Mittelwertes
Die Dichten und Verteilungen zu N(0, 1), N(-2, 1), N(2, 1)
Die Dezile für N(-2, 1):
-3.28155
-2.84162
-2.5244
-2.25335
-2.
Median
-1.74665
-1.4756
-1.15838
-0.718448
Die Dezile für N(2, 1):
0.718448
1.15838
1.4756
1.74665
2.
Median
2.25335
2.5244
2.84162
3.28155
6
4. Variation: Mischungen normal-verteilter Zufallsvariabler
(Siehe z.B. J. Fan, Test of Significance based on Wavelet Thresholding and Neyman's
Truncation, Journal of the American Statistical Association 1996, 682)
Seien X und Y zwei voneinander unabhängig normalverteilte Zufallsvariable, dann
sind (hier ohne Beweis) die folgenden Summen (Mischungen normal-verteilter
Zufallsgrößen) ebenfalls normalverteilt.
Sei Z:= a1.X + a 2.Y, X ~ N(µ1, σ 21), Y ~ N(µ2, σ 22)
dann ist Z ebenfalls normalverteilt, und zwar vom Typ:
2
Z ~ N( Σ a iµ i,
i=1
2
Σ a 2i σ2i )
i=1
für alle Mischungsverhältnisse, Mittelwerte und Varianzen.
Die folgenden Graphiken zeigen zwei Anwendungen:
Mischung 1
Mischung 2
Die durchgezogene Line bezeichnet die (0,1) Variable, die Standard-Normalverteilung.
7
5. Einige Aufschlag-Übungen zur Normalverteilung
Quantile jeder Art
Berücksichtigung der Symmetrie
Eindeutigkeit der Tafel zum Rückrechnen des Mittelwertes bzw. der Varianz
Einige Hauptfälle
1. Der Verteilungswert (Quantil) Die Bestimmung eines α%-Punktes
P[X ist höchstens c], c∈(- ∞, + ∞ )
(die übliche Verteilung)
c-µ
X ~N(µ, σ2): P(X ≤ c) = F(c) = Φ(
): X ~ N(0, 1)
σ
Illustration (Formulierung als Aufgabe)
Es sei µ = 150 und σ2 = 0.25.
a) Berechnen Sie F(µ). (F bezeichnet die Verteilungsfunktion von X.)
b) Berechnen und interpretieren Sie F(150.5).
µ-µ
) = Φ(0) = .5
σ
150.5 - 150.0
zu b) P(X ≤ 150.5) = F(150.5) = Φ(
) = Φ(1) = 0.8413
0.5
Illustration (Formulierung als Aufgabe)
Bestimmen Sie den 75%-Punkt einer normalverteilten Zufallsgröße X, für die gilt
X ~ N(4000, 1 000 000)
Zu dieser Fragestellung wird auch die Umkehrfunktion der Verteilung Φ-1 benutzt:
x 0.75 –4000
x 0.75 –4000
P(X ≤ x0.75 ) = 0.75 = Φ(
) = 0.75 ⇔
= 0.6745 ⇔ x0.75 = 4674.5
1000
1000
Φ-1 (0.75)
= 0.6745
2. Der Schwanz der Verteilung
P[X ist mindestens c], c∈(- ∞, + ∞ )
(der Schwanz der Verteilung)
c-µ
P(X > c) = 1 - F(c) = 1 - Φ(
)
σ
zu a) P(X ≤ µ ) = F(µ ) = Φ(
3. Die Punktwahrscheinlichkeit
P[X ist genau c] = 0, c∈(- ∞, + ∞ )
(eine Frage der Stetigkeit, Unsinn, P ≡ 0)
8
Illustration Aufgabe
Ein Sportfischerverein veranstaltet ein Wettangeln, bei dem derjenige gewinnt, dessen
erste zehn gefangenen Fische das höchste Gesamtgewicht erbringen.
Aus Erfahrung weiß man, daß das Gesamtgewicht von 10 in diesem See gefangenen
Fischen normalverteilt ist mit Erwartungswert µ = 4000 g.
a) Mit welcher Wahrscheinlichkeit ist das Gesamtgewicht der von einem Angler
gefangenen Fische größer als 6 kg, wenn die Varianz 1 000 000 g2 ist?
b) Mit welcher Wahrscheinlichkeit beträgt das Gesamtgewicht der von einem Angler
gefangenen Fische genau 4000 g?
c) Mit Wahrscheinlichkeit 0.7888 beträgt das Gesamtgewicht der zehn von einem
Angler gefangenen Fische zwischen 3 kg und 5 kg. Wie groß ist die Standardabweichung? (s.u. Fall 4)
Lösung: X ~ N(4000, 1 000 000), d.h. µ = 4000, σ2 = 1 000 000
6000 - 4000
) = 1 - Φ(2) = Φ(-2) = 0.0228
1000
b) P(X = 4000) ≡ 0 (eine für stetige Zufallsvariable unsinnige Frage)
a) P(X > 6000) = 1 - P(X ≤ 6000) = 1 - Φ(
4. Die Intervall-Wahrscheinlichkeit
P[ X liegt in einem Bereich (Intervall) (c<d | c,d∈(- ∞, + ∞ )) ]
d-µ
c-µ
P(c ≤ X ≤ d) = F(d) -F(c) = Φ(
) - Φ(
) (die Differenz zweier Verteilungswerte)
σ
σ
Fortsetzung der Illustration der Aufgabe
Wie groß ist die Wahrscheinlichkeit, daß das Gesamtgewicht der zehn von einem
Angler gefangenen Fische zwischen 3 kg und 5 kg beträgt und wenn die Varianz
σ2 = 10002 ist.
Lösungsvariante 1 (µ und σ2, beide Parameter, sind bekannt)
5000 - 4000
3000 - 4000
P(3000 ≤ X ≤ 5000) = Φ(
) - Φ(
)=Φ(1) - Φ(-1) = 0.8413 - 0.1587 = 0.6826
1000
1000
Für die Lösungsvariante 2, daß beide Parameter, µ und σ2, oder einer der beiden
Parameter µ oder σ2 nicht bekannt sind, siehe unten.
9
Illustration (σ-Intervalle)
Für die Intervallbestimmung gibt es für die Normalverteilung eine bedeutsame
Sonder-Anwendung: die σ-Intervalle
P(µ − σ ≤ X ≤ µ + σ)
P(µ − 2σ ≤ X ≤ µ + 2σ)
P(µ − 3σ ≤ X ≤ µ + 3σ) … usw.
µ+σ-µ
µ – σ -µ
) - Φ(
) = Φ(1) - Φ(-1) =
σ
σ
≈ 2/3 Regel (± eine Standardabweichung)
P(µ − σ ≤ X ≤ µ + σ) = F(µ + σ) - F(µ − σ) = Φ(
= 0.6826
µ + 2σ - µ
µ – 2σ - µ
) - Φ(
) = Φ(2) - Φ(-2) =
σ
σ
≈ 95% Regel (± zwei Standardabweichungen)
P(µ - 2σ ≤ X ≤ µ + 2σ) = F(µ +2σ) - F(µ −2σ) = Φ(
= 0.9772 - 0.0228 = 0.9554
µ + 3σ - µ
µ – 3σ - µ
) - Φ(
) = Φ(3) - Φ(-3)=
σ
σ
≈ 100% Regel (± drei Standardabweichungen)
P(µ − 3σ ≤ X ≤ µ + 3σ) = F(µ + 3σ) - F(µ − 3σ) = Φ(
= 0.9987 - 0.0013 = 0.9974
Die inhaltliche Bedeutung ist offensichtlich als Überschlag wichtig: Für
normalverteilte Zufallsgrößen liegen 2/3 bzw. 95% bzw. so gut wie 100% der
Beobachtungen innerhalb der 1- bzw. 2- bzw. 3-σ-Schranken. Entsprechend wichtig ist
die numerische Bestimmung von µ und σ.
10
5. Bestimmen der Lageparameter µ und/oder σ2
Vorgabe eines Tafelwertes und eines der Lageparameter und damit Bestimmen des
fehlenden Lageparameters
Die folgende Kurzschreibweise heißt “aus {…} folgt die rechte Seite vom →”.
c-µ
Fall 1:
{c, Φ(
), µ } → σ2
σ
c-µ
Fall 2:
{c, Φ(
), σ2 } → µ
σ
Vorgabe zweier Tafelwerte und damit Bestimmen beider Lageparameter
c-µ
d-µ
Fall 3:
{c, Φ(
), d, Φ(
) } → (µ, σ2)
σ
σ
Fortsetzung der Illustration der Aufgabe (Bestimmung von σ)
Mit Wahrscheinlichkeit 0.7888 beträgt das Gesamtgewicht der zehn von einem Angler
gefangenen Fische zwischen 3 kg und 5 kg. Wie groß ist die Standardabweichung?
5000 - 4000
3000 - 4000
P(3000 ≤ X ≤ 5000) = Φ(
) - Φ(
) = 0.7888
σ
σ
- 1000
1000
1000
= Φ(
) - Φ(
) = 2Φ(
) - 1 = 0.7888
σ
σ
σ
Zu dieser Fragestellung wird die Umkehrfunktion der Verteilung Φ-1 benutzt (s.u.):
0.7888 gehört in diesem symmetrischen Fall zu zwei Rest-Intervallen der Größe
0.2122/2
= 0.1056 (links in der Verteilung) und
= 0.8944 (rechts in der Verteilung), d.h. aber
Φ(c) = 0.1056 und Φ(d) = 0.8944 = 1 - Φ(c) werden gesucht. Es folgen aus der Tafel
1000
1000
c = -1.245 und d = 1.245, und damit = - 1.245, also σ =
σ
1.245
d.h.
5000 - 4000
3000 - 4000
P(3000 ≤ X ≤ 5000) = 0.7888 ⇔ Φ(
) - Φ(
) = 0.7888
σ
σ
1000
= Φ(d) - Φ(c) =Φ(d) - (1- Φ(d)) = 2Φ(d) - 1 = 2Φ(
) - 1 = 0.7888 ⇔
σ
1000
1000
Φ(
) = 0.5 . 1.7888 = 0.8944 ⇔
= 1.25 ⇒ σ = 800
σ
σ
Φ-1 (0.8944)
= 1.25
11
Fortsetzung der Illustration der Aufgabe (Bestimmung von µ)
Mit Wahrscheinlichkeit 0.7888 beträgt das Gesamtgewicht der zehn von einem Angler
gefangenen Fische zwischen 3 kg und 5 kg, wobei die Varianz 1 000 000 ist. Wie groß ist
der Mittelwert?
Zu dieser Fragestellung wird auch die Umkehrfunktion der Verteilung Φ-1 benutzt. Es
ist eine Anwendung, die ohne weiteres nicht gelingt:
5000 - µ
3000 - µ
P(3000 ≤ X ≤ 5000) = Φ(
) - Φ(
) = 0.7888
1000
1000
Hierfür kann nicht Symmetrie gelten, denn das hieße µ = 4000
5000 - µ
Φ(d) - (1- Φ(d)) = 2Φ(d) - 1 = 2Φ(
) - 1 = 0.7888
1000
5000 - µ
5000 - µ
Φ(
) = 0.5 . 1.7888 = 0.8944 ⇔
= 1.25 ⇒ µ = 3750, ein Widerspruch
1000
1000
Eine zweite Anwendung:
Nun sei µ unbekannt und σ2 = 1 000 000. Außerdem weiß man, daß
P(X > 5000) = 0.8413. Wie groß ist der Mittelwert?
P(X > 5000) = 1 - Φ(
5000 - µ
5000 - µ
5000 - µ
) = 0.8413 ⇔ Φ(
) = 0.1587 ⇔
= -1 ⇔ µ = 6000
1000
1000
1000
Φ-1 (0.1587)
=-1
12
Das Aufschlagen der Tafelwerte aus den Tabellen auf Seiten 25-27 geschieht nach
folgendem Muster, das für zwei Werte illustriert wird.
Das Aufschlagen aus der Φ Tabelle
“Φ(x) = 0.9901“
führt zu x = 2.303,
(Ablesen aus dem Inneren der Tabelle ← ↑ ) bzw. umgekehrt
“x = 2.303”
führt zu Φ(x) = 0.9901
(Ablesen vom Rand der Tabelle → ↓ ).
Φ(x)
…
0.03
…
↑↓
2.30
←→
.9901 = Φ(2.303)
…
Das Aufschlagen aus der Φ−1 Tabelle “x = 1.3787“, führt zu Φ(x) = 0.916,
(Ablesen aus dem Inneren der Tabelle ← ↑ ) bzw. umgekehrt
“Φ(x) = 0.916”
führt zu x = 1.3787
(Ablesen vom Rand der Tabelle → ↓ ).
Φ−1 (x)
…
0.0060
…
↑↓
0.9100
←→
0.916 = Φ−1 (1.3787)
…
13
6 Explizite Bestimmung von Quantilen für stetige parametrische Verteilungen
Das Aufschlagen eines beliebigen Quantils für die Normalverteilung geschieht aus der
Tafel. Es ist ein einfaches Verfahren, aber dennoch eine Hilfskonkonstruktion, wie der
Vergleich zum Bestimmen eines Quantils für andere stetige parametrische Verteilungen zeigt. In vielen anderen stetigen parametrischen Verteilungen kann nämlich das
zu einem Wert α zugehörige xα unmittelbar, ohne jede Tafel, durch Rechnung
explizit bestimmt werden.
Hierzu werden einige Beispiele vorgeführt. Die Parameter a und b sind geeignet
gewählte Konstanten, f und F Dichte und Verteilung und q das Quantil.
Verteilung
1.Gleichverteilung
2.ExponentialVerteilung
f(x) und F(x)
f(x) =
x = F-1 (α) = xα =q, 0≤α≤1
1
x–a
, F(x) =
, a≤x≤b
b –a
b –a
q = a + (b - a) . α, a ≤ b
q = - b . ln(1 - α)
x
1 x
f(x) = e– b , F(x) = 1 - e - b, 0≤x
b
q = b . (-ln(1 - α))1/a
3.WeibullVerteilung
f(x) =
4.Beta-Verteilung
f(x) = a . xa-1 , F(x) = xa , 0≤x≤1
q = α 1/a
5.Beta-Verteilung
f(x) = b(1-x)b-1, F(x) = 1 - (1-x)b, 0≤x≤1
q =1 - (1 - α)1/b
6.ParetoVerteilung
f(x) = aba x - (a+1), F(x) = 1 -
7.Cauchy
f(x) =
a
ba
xa-1
e–
x a
b ,
b
2
F(x) = 1 -
e–
x a
b ,
0≤x
b a
, b≤x
x
q=
b
(1 – α) 1/a
q = a + b tan(π(α - 0.5))
,
π (b2 + (x –a) )
1
x–a
1
F(x) = arctan(
)+ , -∞<x<∞
π
b
2
8.Logistische
Verteilung
f(x) =
e(a–x)/b
b(1+e (a–x)/b )2
, F(x) =
1
q = a - b ln(1/α - 1)
1 + e(a– x)/b
Die Bestimmung des α-Quantils geschieht aus der Umkehrfunktion der Verteilung
dann wie folgt:
α = F(x) ⇒ F-1 (α) = xα ;
x–a
Für die Gleichverteilung ergibt sich z.B. aus α =
das Quantil xα = a + (b-a) . α
b –a
Für den Median: α = 0.5 für die Exponentialverteilung folgt z.B.
x
x
x
α = 1 - e - b ⇔ e - b = 1 - α ⇔ ln(1 - α) = - ⇔ - b . ln(1 - α) = xα ⇔ - b . ln 0.5 = xα
b
14
Für gleichmäßig unterteilte Quantilswerte gibt es feste Namen, z.B. für
die Zweierteilung: der Median
1
i
α = , α = , k=2, i=1,2;
2
k
die Viererteilung: die Quartile
1 2 1 3 4
i
α= ,
= , , = 1, α = , k=4, i=1,2,3,4;
4 4 2 4 4
k
die Fünferteilung: die Quintile
1 2 3 4 5
i
α = , , , , = 1, α = , k=5, i=1,2,3,4,5;
5 5 5 5 5
k
die Zehnerteilung: die Dezile
i
α = 0.1, 0.2, …, 0.8, 0.9, 1.0, α = , k=10, i=1,2, …, 9,10;
k
die Hunderterteilung: die Prozente
i
α = 0.01, 0.02, …, 0.98, 0.99, 1.0, α = , k=100, i=1,2, …, 99,100; usw.
k
7. Einige numerische Beispiele zu Quantilen
Für die Normalverteilung, die Weibull-Verteilung und die Beta-Verteilung werden
einige numerische Aufschlagübungen für die Quantile vorgeführt:
15
1. Die Standard-Normalverteilung zum Vergleich:
Verteilung: normal; Parameter: {0, 1} x: {-3, 3};
Quantile:{0.01, 0.05, 0.5, 0.75, 0.95, 0.99}
Quantil
0.01
0.05
0.50
0.75
0.95
0.99
x-Wert
-2.32635
-1.64485
0.
0.67449
1.64485
2.32635
Einige Aufgaben, bzw. Beispiele illustrieren das Aufschlagen:
Beispiel (Normal-Quantile)
Betrachten Sie die Wahrscheinlichkeit P(X<2) einer N(0,1)-verteilten Zufallsvariablen.
Solch eine Wahrscheinlichkeit α ist in vielen Fragestellungen der schließenden
Statistik schon vorgegeben, und man sucht eine Zahl xα , so daß gerade P(X<x α ) = α.
Beispiel 1:
X sei N(1,4)-verteilt. Wie groß ist x0.5 , so daß also P(X<x0.5 ) = 0.5? Antwort: x0.5 = 1
Eine solche Zahl xα heißt allgemein α-Quantil. Für Spezialfälle gibt es noch andere
Bezeichnungen, z.B. für
α = 0.50 das Quantil x0.5
Median
α = 0.25 das Quantil x0.25
unteres Quartil
α = 0.75 das Quantil x0.75
oberes Quartil.
Lösung: s.o.
Beispiel 2: Berechnen Sie
a) das 0.975-Quantil
b) das 0.025-Quantil
einer N(1, 4)-verteilten Zufallsvariablen X.
Lösung: Quantil x-Wert
0.025
- 2.92
0.975
4.92
16
2. Exponential <-> Weibull-Zusammenhang:
1
Verteilung: exp; Parameter:
x: {0, 6}; Quantile: {0.25, 0.5, 0.75}
4
Quantil
0.25
0.5
0.75
x-Wert
1.15073
2.77259
5.54518
Verteilung: Weibull; Parameter: {1, 4} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
1.15073
2.77259
5.54518
17
3. Weibull-Quantil Darstellung 1
von der Verteilung rechts zur 'x-Achse' links unten
einige alternative Variationen
Verteilung: Weibull; Parameter: {2, 1} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
0.53636
0.832555
1.17741
Verteilung: Weibull; Parameter: {2, 2} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.50
0.75
x-Wert
1.07272
1.66511
2.35482
18
Verteilung: Weibull; Parameter: {2, 3} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
1.60908
2.49766
3.53223
Verteilung: Weibull; Parameter: {2, 4} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
2.14544
3.33022
4.70964
19
Verteilung: Weibull; Parameter: {2, 5} x: {0, 6}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
2.6818
4.16277
5.88705
1/a
Weibull-Quantil Darstellung 2: q = b (-Log[1 - x])
aus der inversen Funktion der Verteilung unten
zur 'x-Achse'(auf der Koordinate nach oben) a= 2; b= 5
20
4. Beta-Verteilungsfunktion F(x) = ax; 0
≤x≤1
Verteilung: Beta; Parameter: {0.5, 1} x: {0, 1}; Quantile: {0.25, 0.5,
Quantil
0.25
0.5
0.75
x-Wert
0.0625
0.25
0.5625.
Beta-Quantil Darstellung:2 q = x
1/a
(Beta-Quantil Darstellung:
q) = x
aus der inversen Funktion der Verteilung unten
zur 'x-Achse'(auf der Koordinate nach oben)
21
Aufgabe (Symmetrische Intervalle um den Mittelwert)
Von einer Zufallsvariablen X kennt man E(X) = var(X) = 100.
Berechnen Sie P(80 ≤ X ≤ 120), wenn
a)
X normalverteilt,
b)
X stetig gleichverteilt, bzw.
c)
X von unbekannter Verteilung ist
Hinweis 1: Für die Normalverteilung gilt E(X) = µ, var(X) = σ2.
Hinweis 2: Für die unbekannte Verteilung ist die Beantwortung mit den bisher verfügbaren Hilfmittel noch nicht möglich, sei hier jedoch schon als Frage vermerkt.
Aufgabe
X sei eine standardnormalverteilte Zufallsvariable N(0,1). Berechnen Sie, bzw.
schlagen Sie auf:
P(X < 0.2) P(- 1.5 ≤ X ≤ 1.5) P(|X| > 0.5)
P(|X| ≥ σ)
Lösung
P(X < 0.2) = 0.5793
P(|X| ≥ σ) = P(|X| ≥ 1) =
= 1 - 0.6826 = 0.3174
(vgl. auch S. 10)
P(|X| ≥ 2σ)
P(X = 7)
P(- 1.5 ≤ X ≤ 1.5) =
= 0.8664
P(|X| > 0.5) =
= 1 - 0.3830 = 0.6170
P(|X| ≥ 2σ) = P(|X| ≥ 2) =
= 1 - 0.9544 = 0.0456
!
P(X = 7) = 0
22
Aufgabe (kleinste und größte Intervalle)
Eine Zufallsvariable X sei nach N(2,4) verteilt. Bestimmen Sie
a) ein x∈R derart, daß gilt
b) das kürzeste Intervall [x1, x2] derart, daß gilt
P(x ≤ X)=0.75
P(x1≤ X ≤x2)=0.8.
c) ein möglichst großes (möglicherweise offenes) Intervall mit
P(x1≤ X ≤x2)=0.8.
Lösung
X-2 x-2
x-2
a) P(x ≤ X) = 0.75 ⇔ P(X ≤ x) = 0.25 ⇔ P(
≤
) = Φ(
) = 0.25
2
2
2
x–2
aus der Tafel (s.u.) folgt:
= - 0.675 ⇔ x = 0.65
2
b) Gesucht wird P(x1 ≤ X ≤ x2) = 0.8, Symmetrie und Stetigkeit verlangen links und
rechts vom gesuchten Intervall zwei gleichgroße Rest-Intervalle:
P(X < x1) = P(X > x2) = 0.1
x1 - 2
P(X < x1) = P(X ≤ x1) = 0.1 ⇒
= - 1.282 ⇒ x1 - 2 = - 2.564 ⇒ x1 = - 0.564
2
"Das Intervall ist symmetrisch zu µ=2", also x2 = 4.564 ∴ I = [-0.564, 4.564]
x2 - 2
X - 2 x2 - 2
c) Setze x1 = -∞ : P(X ≤ x2) = 0.8 ⇔ P(
≤
) = 0.8 ⇔ Φ(
) = 0.8
2
2
2
x -2
⇔ 2
= 0.842 ⇔ x2 - 2 = 1.684 ⇔ x2 = 3.684: ∴ I = (- ∞ , 3.684]
2
Eine Alternative ist, die rechte Intervallgrenze auf ‘+ ∞’ zu setzen.
Aufgabe (kleinste und größte Intervalle)
Sei X normalverteilt mit µ = 2 und σ2 = 9. Bestimmen Sie ein 90% Intervall
a) in beliebiger Lage,
b) von möglichst kleiner Länge,
c) von möglichst großer Länge.
Lösung
X~N(2, 9); zum Benutzen der Tafel der Standard-Normalverteilung X* ~ N(0,1) gilt
x–µ
x* =
⇔ x = σ · x* + µ
σ
Dabei wird die Symmetrie zum Mittelwert und die Lage des Maximums der Dichte
(des Modus) beachtet. Für a) und b) folgen
P(x0 ≤X ≤x1)= 0.9 ⇔ P(x0* ≤ X* ≤ x1*)= 0.9 ⇔
x0*= -1.645 und x1*= 1.645 ⇔ x1= -1.645 · 3 + 2 = -2.935, x2 = 1.645 · 3 + 2 = 6.935
Für a) und c) sei das Intervall (-∞, x] und damit
P(-∞ < X ≤ x)= 0.9 ⇔ F(x)= 0.9 ⇔ Φ(x*)= 0.9 ⇔ x*= 1.282 ⇔ x= 3 · 1.282 + 2 = 5.846
23
8. Die halb-normale Verteilung
Eine in der Wirtschaftstheorie erforderliche Modifikation ist die sog. halb-normale
Verteilung. Die zugehörige Dichte ist
f: (-∞,µ]→R
f(x) :=
2
2
e
-
(x-µ)
2σ
2
2
,x≤µ
2πσ
in der die Variable auf eine Halbachse beschränkt ist.
9. Die lognormale Verteilung
Eine verwandte Verteilung ist die lognormale Verteilung.
Eine Zufallsvariable X mit der Dichte
f: R→R
f(x) :=
1
2πσ
1
.e
2 x
.
-
(lnx-a)
2σ
2
2
2
, x>0, σ >0, a∈R
heißt lognormal-verteilt mit Parametern a und σ2.
Diese Dichte spielt ähnlich wie die Pareto-Verteilung in Größenverteilungen eine
Rolle.
10. Ein Bild der Normal-Verteilung
(nach W. J. Youden, The American Statistician, April-May, 1950, p. 11, bottom, bzw.
W. J. Youden, Topographical delight of a statistican, Multifunctioning graphical
elements, 143)
DIE
N O R M A LODER GAUSS VERTEILUNG IST EINES
DER HERVORRAGENDSTEN
ERGEBNISSE DER STATISTIK UND
DER MENSCHLICHEN ERKENNTNIS
ALLGEMEIN * SIE IST HEUTE EIN NAHEZU
UNENTBEHRLICHER BEGRIFF FUER DIE EMPIRISCHE FORSCHUNG IN DER NATUR- UND SOZIALWISSENSCHAFT, IN MEDIZIN, LANDWIRTSCHAFT UND
INGENIEURWISSENSCHAFTEN * FUER DIE ANALYSE VON DATEN UND
GRUNDWISSEN, DIE SICH AUS BEOBACHTUNG UND EXPERIMENT AUFBAUEN.
Typische Beispiele normalverteilter Größen sind: Größe und Gewicht von Früchten,
z.B. Maiskolben, Äpfel, Bananen; Größe und Gewicht von Mensch und Tier;
Meßfehler; Krankheitsdauern, Fluthöhen; ….
24
11. Weitere Aufgaben
Aufgabe 1
a) Beweisen Sie für die Dichtefunktion f der N(µ, σ2)-Verteilung:
1. f ist symmetrisch um µ, d.h. ∀x∈R: f(µ - x) = f(µ + x).
2. µ ist Maximalstelle von f.
3. f ist streng konvex für x∈(-∞, µ - σ) ∪ (µ + σ, ∞)
und streng konkav für x∈(µ - σ, µ + σ).
b) Berechnen Sie für eine N(µ, σ2)-verteilte Zufallsvariable X die Wahrscheinlichkeiten P(µ - kσ ≤ X ≤ µ + kσ) mit k = 1, 2, 3.
c) Berechnen Sie für eine Zufallsvariable X mit Erwartungswert E(X) und Varianz
var(X) untere Schranken für die Wahrscheinlichkeiten
P( E(X) - k . var(X) ≤ X ≤ E(X) + k . var(X) ) mit k = 1, 2, 3.
Aufgabe 2 (eine bedeutsame, aber auch anspruchsvollere Frage)
Die Stutzung einer Verteilung: Sei eine Zufallsvariable X beliebig über dem Intervall
[a1,b1] verteilt und sei A das Ereignis, daß X auf ein Teilintervall [a2,b2], a1≤a2, b2≤b1
eingeschränkt sei, z.B. für die Normalverteilung N (0, σ2) a1= -∞, b1= +∞ und a2= -σ, b 2=
+σ. Zeigen Sie , daß, falls F(x) eine Verteilung über [a1, b 1] ist, F(x|A) eine Verteilung
F(x) -F(a 2)
über [a2, b2] ist und F (x|A) =
.
F(b 2) - F( a2)
12. Die Standard-Normal-Tafeln
Hierzu siehe die drei folgenden Seiten bzw. die zu der Vorlesung zugehörige
Formelsammlung.
25
Tafel 1
Die Normalverteilung Φ(x)
+------+-------------------------------------------------------------+
| x
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09 |
+------+-------------------------------------------------------------+
| -3.00| .0013 .0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 |
| -2.90| .0019 .0018 .0018 .0017 .0016 .0016 .0015 .0015 .0014 .0014 |
| -2.80| .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 |
| -2.70| .0035 .0034 .0033 .0032 .0031 .0030 .0029 .0028 .0027 .0026 |
| -2.60| .0047 .0045 .0044 .0043 .0041 .0040 .0039 .0038 .0037 .0036 |
| -2.50| .0062 .0060 .0059 .0057 .0055 .0054 .0052 .0051 .0049 .0048 |
| -2.40| .0082 .0080 .0078 .0075 .0073 .0071 .0069 .0068 .0066 .0064 |
| -2.30| .0107 .0104 .0102 .0099 .0096 .0094 .0091 .0089 .0087 .0084 |
| -2.20| .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 |
| -2.10| .0179 .0174 .0170 .0166 .0162 .0158 .0154 .0150 .0146 .0143 |
| -2.00| .0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 |
| -1.90| .0287 .0281 .0274 .0268 .0262 .0256 .0250 .0244 .0239 .0233 |
| -1.80| .0359 .0351 .0344 .0336 .0329 .0322 .0314 .0307 .0301 .0294 |
| -1.70| .0446 .0436 .0427 .0418 .0409 .0401 .0392 .0384 .0375 .0367 |
| -1.60| .0548 .0537 .0526 .0516 .0505 .0495 .0485 .0475 .0465 .0455 |
| -1.50| .0668 .0655 .0643 .0630 .0618 .0606 .0594 .0582 .0571 .0559 |
| -1.40| .0808 .0793 .0778 .0764 .0749 .0735 .0721 .0708 .0694 .0681 |
| -1.30| .0968 .0951 .0934 .0918 .0901 .0885 .0869 .0853 .0838 .0823 |
| -1.20| .1151 .1131 .1112 .1093 .1075 .1056 .1038 .1020 .1003 .0985 |
| -1.10| .1357 .1335 .1314 .1292 .1271 .1251 .1230 .1210 .1190 .1170 |
| -1.00| .1587 .1562 .1539 .1515 .1492 .1469 .1446 .1423 .1401 .1379 |
| -.90| .1841 .1814 .1788 .1762 .1736 .1711 .1685 .1660 .1635 .1611 |
| -.80| .2119 .2090 .2061 .2033 .2005 .1977 .1949 .1922 .1894 .1867 |
| -.70| .2420 .2389 .2358 .2327 .2296 .2266 .2236 .2206 .2177 .2148 |
| -.60| .2743 .2709 .2676 .2643 .2611 .2578 .2546 .2514 .2483 .2451 |
| -.50| .3085 .3050 .3015 .2981 .2946 .2912 .2877 .2843 .2810 .2776 |
| -.40| .3446 .3409 .3372 .3336 .3300 .3264 .3228 .3192 .3156 .3121 |
| -.30| .3821 .3783 .3745 .3707 .3669 .3632 .3594 .3557 .3520 .3483 |
| -.20| .4207 .4168 .4129 .4090 .4052 .4013 .3974 .3936 .3897 .3859 |
| -.10| .4602 .4562 .4522 .4483 .4443 .4404 .4364 .4325 .4286 .4247 |
|
.00| .5000 .4960 .4920 .4880 .4840 .4801 .4761 .4721 .4681 .4641 |
+------+-------------------------------------------------------------+
| x
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09 |
+------+-------------------------------------------------------------+
26
Die Normalverteilung Φ(x)
+------+-------------------------------------------------------------+
| x
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09 |
+------+-------------------------------------------------------------+
|
.00| .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359 |
|
.10| .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 |
|
.20| .5793 .5832 .5871 .5910 .5948 .5987 .6026 .6064 .6103 .6141 |
|
.30| .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 |
|
.40| .6554 .6591 .6628 .6664 .6700 .6736 .6772 .6808 .6844 .6879 |
|
.50| .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 |
|
.60| .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 |
|
.70| .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 |
|
.80| .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 |
|
.90| .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 |
| 1.00| .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 |
| 1.10| .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 |
| 1.20| .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015 |
| 1.30| .9032 .9049 .9066 .9082 .9099 .9115 .9131 .9147 .9162 .9177 |
| 1.40| .9192 .9207 .9222 .9236 .9251 .9265 .9279 .9292 .9306 .9319 |
| 1.50| .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441 |
| 1.60| .9452 .9463 .9474 .9484 .9495 .9505 .9515 .9525 .9535 .9545 |
| 1.70| .9554 .9564 .9573 .9582 .9591 .9599 .9608 .9616 .9625 .9633 |
| 1.80| .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9699 .9706 |
| 1.90| .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767 |
| 2.00| .9772 .9778 .9783 .9788 .9793 .9798 .9803 .9808 .9812 .9817 |
| 2.10| .9821 .9826 .9830 .9834 .9838 .9842 .9846 .9850 .9854 .9857 |
| 2.20| .9861 .9864 .9868 .9871 .9875 .9878 .9881 .9884 .9887 .9890 |
| 2.30| .9893 .9896 .9898 .9901 .9904 .9906 .9909 .9911 .9913 .9916 |
| 2.40| .9918 .9920 .9922 .9925 .9927 .9929 .9931 .9932 .9934 .9936 |
| 2.50| .9938 .9940 .9941 .9943 .9945 .9946 .9948 .9949 .9951 .9952 |
| 2.60| .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964 |
| 2.70| .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974 |
| 2.80| .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981 |
| 2.90| .9981 .9982 .9982 .9983 .9984 .9984 .9985 .9985 .9986 .9986 |
| 3.00| .9987 .9987 .9987 .9988 .9988 .9989 .9989 .9989 .9990 .9990 |
+------+-------------------------------------------------------------+
| x
.00
.01
.02
.03
.04
.05
.06
.07
.08
.09 |
+------+-------------------------------------------------------------+
27
Tafel 2 Die Umkehrfunktion der Normalverteilung Φ(x): Φ−1 (x)
Φ(x)\ .0000 .0010 .0020 .0030 .0040 .0050 .0060 .0070 .0080 .0090
---------------------------------------------------------------------------.5000| .0000 .0025 .0050 .0075 .0100 .0125 .0150 .0175 .0201 .0226
.5100| .0251 .0276 .0301 .0326 .0351 .0376 .0401 .0426 .0451 .0476
.5200| .0502 .0527 .0552 .0577 .0602 .0627 .0652 .0677 .0702 .0728
.5300| .0753 .0778 .0803 .0828 .0853 .0878 .0904 .0929 .0954 .0979
.5400| .1004 .1030 .1055 .1080 .1105 .1130 .1156 .1181 .1206 .1231
.5500| .1257 .1282 .1307 .1332 .1358 .1383 .1408 .1434 .1459 .1484
.5600| .1510 .1535 .1560 .1586 .1611 .1637 .1662 .1687 .1713 .1738
.5700| .1764 .1789 .1815 .1840 .1866 .1891 .1917 .1942 .1968 .1993
.5800| .2019 .2045 .2070 .2096 .2121 .2147 .2173 .2198 .2224 .2250
.5900| .2275 .2301 .2327 .2353 .2378 .2404 .2430 .2456 .2482 .2508
.6000| .2533 .2559 .2585 .2611 .2637 .2663 .2689 .2715 .2741 .2767
.6100| .2793 .2819 .2845 .2871 .2898 .2924 .2950 .2976 .3002 .3029
.6200| .3055 .3081 .3107 .3134 .3160 .3186 .3213 .3239 .3266 .3292
.6300| .3319 .3345 .3372 .3398 .3425 .3451 .3478 .3505 .3531 .3558
.6400| .3585 .3611 .3638 .3665 .3692 .3719 .3745 .3772 .3799 .3826
.6500| .3853 .3880 .3907 .3934 .3961 .3989 .4016 .4043 .4070 .4097
.6600| .4125 .4152 .4179 .4207 .4234 .4261 .4289 .4316 .4344 .4372
.6700| .4399 .4427 .4454 .4482 .4510 .4538 .4565 .4593 .4621 .4649
.6800| .4677 .4705 .4733 .4761 .4789 .4817 .4845 .4874 .4902 .4930
.6900| .4959 .4987 .5015 .5044 .5072 .5101 .5129 .5158 .5187 .5215
.7000| .5244 .5273 .5302 .5330 .5359 .5388 .5417 .5446 .5476 .5505
.7100| .5534 .5563 .5592 .5622 .5651 .5681 .5710 .5740 .5769 .5799
.7200| .5828 .5858 .5888 .5918 .5948 .5978 .6008 .6038 .6068 .6098
.7300| .6128 .6158 .6189 .6219 .6250 .6280 .6311 .6341 .6372 .6403
.7400| .6433 .6464 .6495 .6526 .6557 .6588 .6620 .6651 .6682 .6713
.7500| .6745 .6776 .6808 .6840 .6871 .6903 .6935 .6967 .6999 .7031
.7600| .7063 .7095 .7128 .7160 .7192 .7225 .7257 .7290 .7323 .7356
.7700| .7388 .7421 .7454 .7488 .7521 .7554 .7588 .7621 .7655 .7688
.7800| .7722 .7756 .7790 .7824 .7858 .7892 .7926 .7961 .7995 .8030
.7900| .8064 .8099 .8134 .8169 .8204 .8239 .8274 .8310 .8345 .8381
.8000| .8416 .8452 .8488 .8524 .8560 .8596 .8633 .8669 .8705 .8742
.8100| .8779 .8816 .8853 .8890 .8927 .8965 .9002 .9040 .9078 .9116
.8200| .9154 .9192 .9230 .9269 .9307 .9346 .9385 .9424 .9463 .9502
.8300| .9542 .9581 .9621 .9661 .9701 .9741 .9782 .9822 .9863 .9904
.8400| .9945 .9986 1.0027 1.0069 1.0110 1.0152 1.0194 1.0237 1.0279 1.0322
.8500| 1.0364 1.0407 1.0450 1.0494 1.0537 1.0581 1.0625 1.0669 1.0714 1.0758
.8600| 1.0803 1.0848 1.0893 1.0939 1.0985 1.1031 1.1077 1.1123 1.1170 1.1217
.8700| 1.1264 1.1311 1.1359 1.1407 1.1455 1.1503 1.1552 1.1601 1.1650 1.1700
.8800| 1.1750 1.1800 1.1850 1.1901 1.1952 1.2004 1.2055 1.2107 1.2160 1.2212
.8900| 1.2265 1.2319 1.2372 1.2426 1.2481 1.2536 1.2591 1.2646 1.2702 1.2759
.9000| 1.2816 1.2873 1.2930 1.2988 1.3047 1.3106 1.3165 1.3225 1.3285 1.3346
.9100| 1.3408 1.3469 1.3532 1.3595 1.3658 1.3722 1.3787 1.3852 1.3917 1.3984
.9200| 1.4051 1.4118 1.4187 1.4255 1.4325 1.4395 1.4466 1.4538 1.4611 1.4684
.9300| 1.4758 1.4833 1.4909 1.4985 1.5063 1.5141 1.5220 1.5301 1.5382 1.5464
.9400| 1.5548 1.5632 1.5718 1.5805 1.5893 1.5982 1.6072 1.6164 1.6258 1.6352
.9500| 1.6449 1.6546 1.6646 1.6747 1.6849 1.6954 1.7060 1.7169 1.7279 1.7392
.9600| 1.7507 1.7624 1.7744 1.7866 1.7991 1.8119 1.8250 1.8384 1.8522 1.8663
.9700| 1.8808 1.8957 1.9110 1.9268 1.9431 1.9600 1.9774 1.9954 2.0141 2.0335
.9800| 2.0537 2.0749 2.0969 2.1201 2.1444 2.1701 2.1973 2.2262 2.2571 2.2904
.9900| 2.3263 2.3656 2.4089 2.4573 2.5121 2.5758 2.6521 2.7478 2.8782 3.0902
---------------------------------------------------------------------------Φ(x)/ .0000 .0010 .0020 .0030 .0040 .0050 .0060 .0070 .0080 .0090