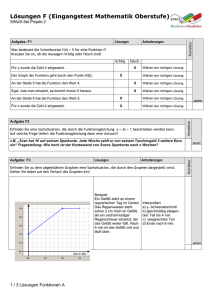
Checkliste für lineare Funktionen

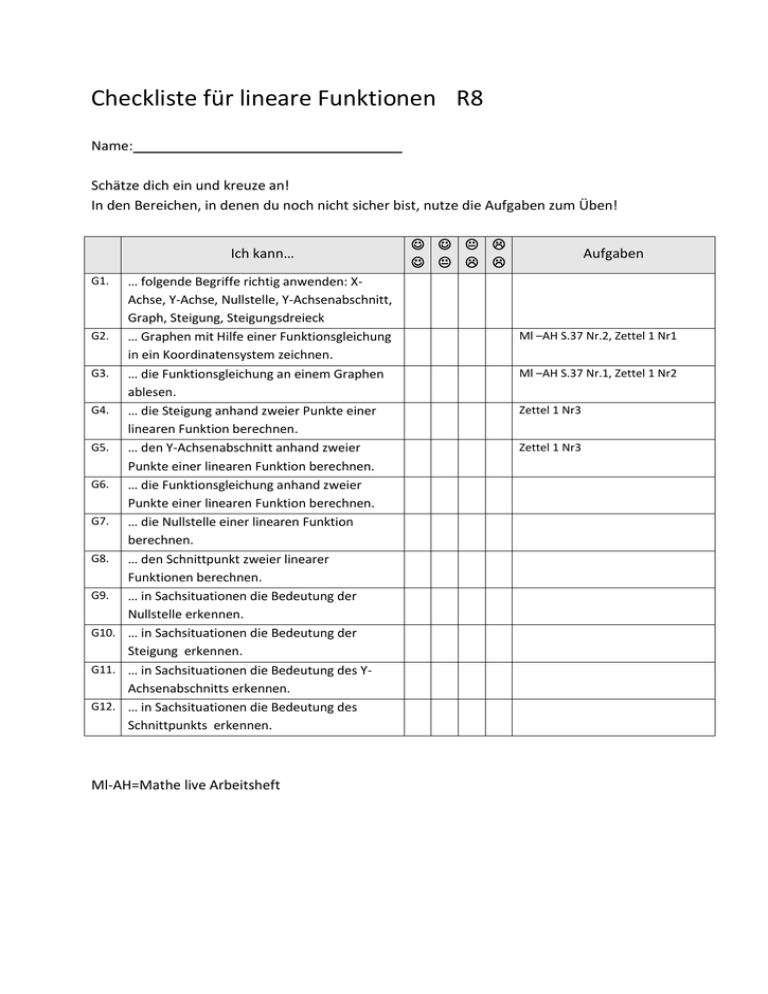
Checkliste für lineare Funktionen R8
Name:
Schätze dich ein und kreuze an!
In den Bereichen, in denen du noch nicht sicher bist, nutze die Aufgaben zum Üben!
Ich kann…
   
   
Aufgaben
G1.
… folgende Begriffe richtig anwenden: XAchse, Y-Achse, Nullstelle, Y-Achsenabschnitt,
Graph, Steigung, Steigungsdreieck
G2. … Graphen mit Hilfe einer Funktionsgleichung
in ein Koordinatensystem zeichnen.
G3. … die Funktionsgleichung an einem Graphen
ablesen.
G4. … die Steigung anhand zweier Punkte einer
linearen Funktion berechnen.
G5. … den Y-Achsenabschnitt anhand zweier
Punkte einer linearen Funktion berechnen.
G6. … die Funktionsgleichung anhand zweier
Punkte einer linearen Funktion berechnen.
G7. … die Nullstelle einer linearen Funktion
berechnen.
G8. … den Schnittpunkt zweier linearer
Funktionen berechnen.
G9. … in Sachsituationen die Bedeutung der
Nullstelle erkennen.
G10. … in Sachsituationen die Bedeutung der
Steigung erkennen.
G11. … in Sachsituationen die Bedeutung des YAchsenabschnitts erkennen.
G12. … in Sachsituationen die Bedeutung des
Schnittpunkts erkennen.
Ml-AH=Mathe live Arbeitsheft
Ml –AH S.37 Nr.2, Zettel 1 Nr1
Ml –AH S.37 Nr.1, Zettel 1 Nr2
Zettel 1 Nr3
Zettel 1 Nr3
G1
Anhang der Checkliste für lineare Funktionen
R8
y
Steigungsdreieck
Y-Achsenabschnitt
Steigung=
5
Nullstelle
x
-5
5
Graph
-5
X-Achse
Y-Achse
=2
G2
Anhang der Checkliste für lineare Funktionen
R8
Eine Funktionsgleichung y = x + 2 ist gegeben.
y
1. Schritt: Zeichne einen Punkt beim YAchsenabschnitt.
2. Schritt: Zeichne ein Steigungsdreieck mit der
Steigung
3. Schritt: Zeichne dort einen Punkt.
4. Schritt: Zeichne den Graphen durch die
Punkte.
Tipps: Wenn die Steigung negativ ist, geht das
Steigungsdreieck nach unten.
Wenn die Steigung aus einer ganzen Zahl besteht,
gehst du einen Schritt nach rechts und dann nach
oben bzw. nach unten.
5
X
X
-5
5
x
-5
G3
Anhang der Checkliste für lineare Funktionen
R8
Ein Graph ist gegeben.
y
1. Schritt: Lies den Y-Achsenabschnitt ab.
Hier ist b=
2. Schritt: Zeichne ein Steigungsdreieck und lies
die Steigung ab.
Hier
3. Schritt: Setze in die Funktionsgleichung ein.
5
-5
5
-5
Tipps: Wenn die Steigung negativ ist, geht das
Steigungsdreieck nach unten.
Wenn die Steigung aus einer ganzen Zahl besteht,
gehst du einen Schritt nach rechts und dann nach oben bzw. nach unten.
x
G4
Anhang der Checkliste für lineare Funktionen
R8
Gegeben sind zwei Punkte einer linearen Funktion und du sollst die Steigung der Funktion
berechnen, gehe folgendermaßen vor:
Punkt 1 = (x1/y1) und Punkt 2 = (x2/y2)
Die Steigung ist die Differenz der y-Koordinaten (Höhe) durch die Differenz der xKoordinaten (Breite).
Berechne:
G5
Anhang der Checkliste für lineare Funktionen
R8
Wenn die Steigung (z.B. m=4) und ein Punkt (z.B. P=(2/3)) einer linearen Funktion gegeben
ist und du sollst den Y-Achsenabschnitt b berechnen, gehe folgendermaßen vor:
Die allgemeine Funktionsgleichung lautet
Also ist der Y-Achsenabschnitt
.
G6
Anhang der Checkliste für lineare Funktionen
R8
Gegeben sind zwei Punkte einer linearen Funktion und du sollst die Funktionsgleichung
berechnen, gehe folgendermaßen vor:
1. Schritt: Berechne die Steigung (siehe G4)
2. Schritt: Berechne den Y-Achsenabschnitt (siehe G5)
3. Schritt: Setze m und b in die allgemeine Funktionsgleichung
ein.
G7
Anhang der Checkliste für lineare Funktionen
Du hast eine Funktionsgleichung
R8
und du sollst die Nullstelle berechnen:
Bei der Nullstelle ist der y-Wert gleich Null, deshalb setzt du die Gleichung gleich Null:
Also ist die Nullstelle bei (1,5/0).
G8
Anhang der Checkliste für lineare Funktionen
R8
Du hast zwei Funktionsgleichungen und sollst den Schnittpunkt berechnen.
Funktion 1:
und Funktion 2:
Im Schnittpunkt sind die x-Werte und die y-Werte beider Funktionen gleich, deshalb werden
die Funktionsgleichungen gleich gesetzt.
Nun wird der berechnete x-Wert in eine Funktion eingesetzt:
(Tipp: Man kann die Probe machen, indem man noch mal in die andere Gleichung einsetzt.)
Der Schnittpunkt ist S=(
)
G9
Anhang der Checkliste für lineare Funktionen
R8
Was bedeutet die Nullstelle in einer Sachsituation?
Größe der Kerze oder Geld auf dem
Sparguthaben oder Liter im Pool
Nullstelle!!
Zeit
Zu diesem Zeitpunkt ist entweder die Kerze abgebrannt, das Geld alle oder der Pool leer.
Die Nullstelle bedeutet meist, dass in einer Situation etwas nicht mehr da ist, also „auf
Null geht“.
G10
Anhang der Checkliste für lineare Funktionen
R8
Was bedeutet die Steigung in einer Sachsituation?
Die Steigung ist immer der Änderungsfaktor pro Einheit.
Bei negativer Steigung ist dies der Abnahmefaktor:
Um wie viel nimmt das Geld, die Länge, die Menge… in einer Einheit ab.
Bei positiver Steigung ist dies der Zunahmefaktor:
Um wie viel steigt die Menge, der Preis,… pro Einheit an.
Ist die Steigung gleich Null, das heißt ist die Funktion konstant, ändert sich nichts, zum
Beispiel bei einer Flatrate oder einem Festpreis.
G11
Anhang der Checkliste für lineare Funktionen
R8
Was bedeutet der Y-Achsenabschnitt in einer Sachsituation?
Der Y-Achsenabschnitt ist meist der Anfangszustand einer Situation,
zum Beispiel wie viel war vor dem Abpumpen im Pool oder wie lang war die Kerze.
Er kann auch die Grundgebühr in einigen Situationen bedeuten,
zum Beispiel eine Telefongrundgebühr oder eine Grundgebühr beim Strompreis.
G12
Anhang der Checkliste für lineare Funktionen
R8
Was bedeutet der Schnittpunkt in einer Sachsituation?
Preis
Tarif 1
Schnittpunkt
Tarif 2
Minuten
Im Schnittpunkt kosten beide Tarife bei gleicher Minutenzahl gleich viel. Vorher ist Tarif 1
billiger, danach ist Tarif 2 billiger.
Allgemein bedeutet der Schnittpunkt, dass in diesem Punkt irgendetwas
gleich ist.