3. Die Umwandlung der Formen komplexer Zahlen

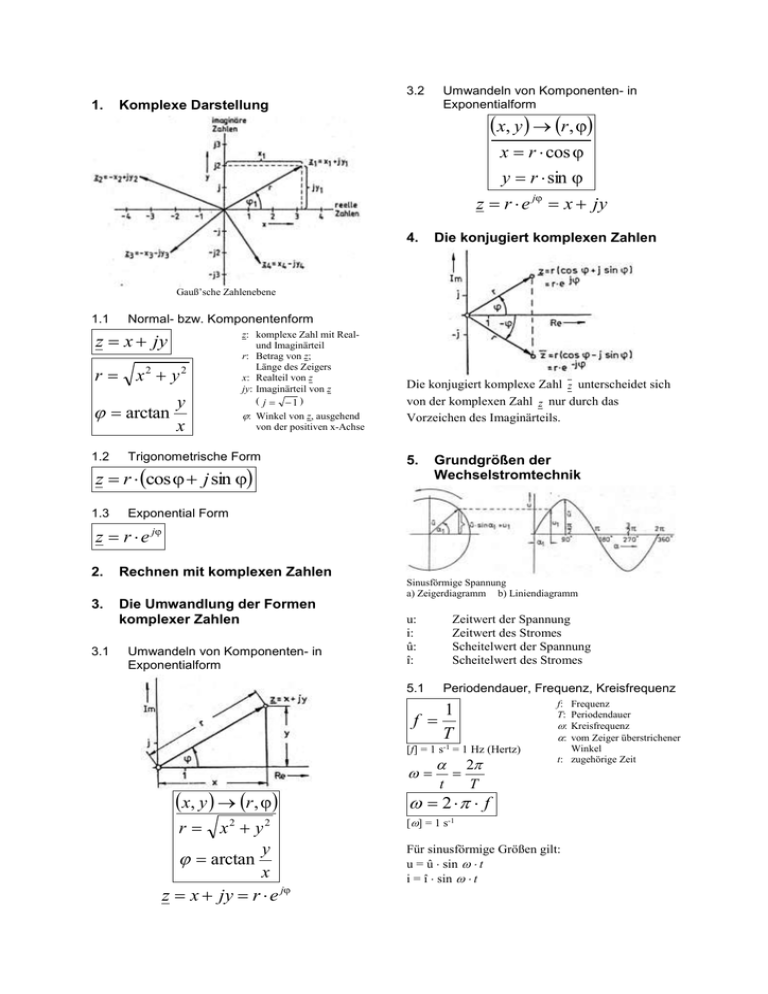
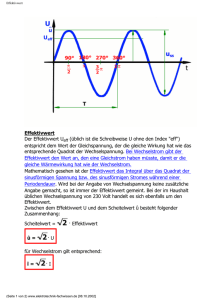
3.2
1.
Komplexe Darstellung
Umwandeln von Komponenten- in
Exponentialform
x, y   r , 
x  r  cos 
y  r  sin 
z  r  e j  x  jy
4.
Die konjugiert komplexen Zahlen
Gauß’sche Zahlenebene
1.1
Normal- bzw. Komponentenform
z  x  jy
z: komplexe Zahl mit Realund Imaginärteil
r: Betrag von z;
Länge des Zeigers
x: Realteil von z
jy: Imaginärteil von z
( j  1 )
r  x2  y 2
  arctan
y
x
: Winkel von z, ausgehend
von der positiven x-Achse
1.2
Trigonometrische Form
1.3
Exponential Form
Die konjugiert komplexe Zahl z unterscheidet sich
von der komplexen Zahl z nur durch das
Vorzeichen des Imaginärteils.
5.
z  r  cos   j sin 
Grundgrößen der
Wechselstromtechnik
z  r  e j
2.
Rechnen mit komplexen Zahlen
Sinusförmige Spannung
a) Zeigerdiagramm b) Liniendiagramm
3.
3.1
Die Umwandlung der Formen
komplexer Zahlen
Umwandeln von Komponenten- in
Exponentialform
u:
i:
û:
î:
5.1
Zeitwert der Spannung
Zeitwert des Stromes
Scheitelwert der Spannung
Scheitelwert des Stromes
Periodendauer, Frequenz, Kreisfrequenz
f:
T:
:
:
1
f 
T
[f] = 1 s-1 = 1 Hz (Hertz)

x, y   r , 
r x y
y
  arctan
x
z  x  jy  r  e j
2
2

t

2
T
Frequenz
Periodendauer
Kreisfrequenz
vom Zeiger überstrichener
Winkel
t: zugehörige Zeit
  2   f
[] = 1 s-1
Für sinusförmige Größen gilt:
u = û  sin   t
i = î  sin   t
5.2
Spitze-Spitze-Wert
iSS  2 iˆ
5.3
bzw.
uSS  2 uˆ
Bei sinusförmigen Größen ist:
i
Mittelwerte der Wechselstromgrößen
5.3.1 Arithmetischer Mittelwert
(Gleichrichtwert)
u
2  iˆ

 0,637  iˆ
2  uˆ
i, u : Artithmetischer
Mittelwert von Strom
und Spannung
 0,637  uˆ

5.3.2 Quadratischer Mittelwert und
Effektivwert
Für beliebige Kurveformen gilt:
i* 
i1  i2  i3  ...  in 1 n
  ik
n
n k 1
Quadratischer Mittelwert
i1  i2  i3  ...  in
1 n 2
I 
  ik
n
n k 1
2
2
2
2
2
Für die Spannung gilt:
U2 
1 n 2
 uk
n k 1
Die exakte Lösung mittels der Integralrechnung
ergibt für sinusförmige Größen:
iˆ 2
I 
2
2
uˆ 2
und U 
2
2
Effektivwert
iˆ 2
iˆ
I

 0,707  iˆ
2
2
uˆ 2
uˆ
U

 0,707  uˆ
2
2
I², U²:
I, U:
Quadratischer Mittelwert von Strom und Spannung
Effektivwert von Strom und Spannung
5.3.3 Scheitelfaktor (sinus)
iˆ
iˆ
iˆ  2


 2  1,414
I
iˆ
iˆ
2
5.3.4 Formfaktor (sinus)
uˆ
U
uˆ  

 2 

 1,11
u 2  uˆ 2  2  uˆ 2  2

5.3.5 Kennwerte von Wechselstromformen
i1 = î1  sin (   t + 0°) und
i2 = î2  sin (   t + 2)
Im Zeigerdiagramm geometrisch addiert wird:
ig = i1 + i2
Summenstrom:
ig  iˆg  sin t  
6.
6.1
x:
ig:
Nullphasenwinkel des
Summenstroms
Summenstrom
Wechselstromwiderstände
Ohmscher Widerstand
Belastung eines Wechselstromgenerators (G) durch einen
Ohmschen Widerstand
5.4
1.
2.
5.5
Nullsphasenwinkel,
Phasenverschiebung
Der Winkel, den die Zeiger gegenüber der
Bezugsachse bilden, wird Nullphasenwinkel
genannt.
Er ist bezugspunktabhängig
Die Augenblickswert-Gleichungen für die
Spannung lauten:
u1 = û1  sin (   t + 1)
u2 = û2  sin (   t + 2)
Die Differenz der Nullphasenwinkel beider
sinusförmigen Spannungen wird
Phasenverschiebuingswinkel  genannt.
Seine Größe ergibt sich zu:
 = 2 + 1
Addition von Wechselgrößen
Liniendiagramm für u und i bei Belastung durch R
Für den Scheitelwert:
û=îR
Für den Effektivwert:
U  R I
Phasenverschiebungswinkel:
  0
6.2
Induktiver Wiederstand
Belastung eines Wechselstromgenerators durch eine Induktivität.
Addition von Wechselgrößen unterschiedlicher Phasenlage
a) Zeigerdiagramm
b) Liniendiagramm
Für die Augenblickswerte ist:
Für den Effektivwert:
U
I
 U   C
XC
XC 
XC: Kapazitiver
Blindwiderstand
1
 C
Phasenverschiebungswinkel zwischen Strom und
Spannung (Bezugsgröße Strom!)  = - 90°
Liniendiagramm für u und i bei rein induktiver Belastung
Für den Scheitelwert:
û=îL
Für den Effektivwert:
U  I   L  I  X L
XL: induktiver
Blindwiderstand
XL   L
Phasenverschiebungswinkel zwischen Strom und
Spannung (Bezugsgröße Strom!)  = 90°
6.3
Kapazitiver Widerstand
Belastung eines Wechselstromgenerators durch eine Kapazität.
Liniendiagramm für u und i bei rein kapazitiver Belastung
Für den Scheitelwert des Stromes:
1
iˆ  uˆ    C  uˆ  1
 C