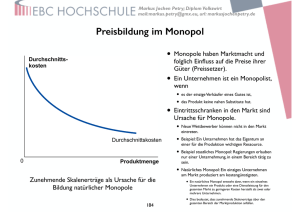
Wettbewerb SS 2016
Werbung

Wettbewerb SS 2016 Prof. Dr. Susanne Soretz Worum wird es gehen? Arbeitsteilung macht Koordinationsmechanismus unverzichtbar ➜ Märkte erfüllen diese Funktion am besten bei vollkommenem Wettbewerb sind Marktergebnisse Pareto-optimal Marktversagen führt zu Fehlallokationen Unternehmen mit Marktmacht (Monopole, Oligopole) verhalten sich anders als Mengenanpasser, in der Regel geringeres Angebot zu höheren Preisen, dadurch wird die Informationsfunktion der Preise gestört, es entstehen Wohlfahrtsverluste Wettbewerbspolitik: Regulierung soll Marktmacht reduzieren bzw. Marktergebnisse korrigieren Prof. Dr. Susanne Soretz Wettbewerb SS 2016 1 / 190 Gliederung 1. Einführung und Überblick: Warum Wettbewerb? 2. Das allg. Gleichgewicht und das 1. Wohlfahrtstheorem: Pareto–Optimum — Wettbewerbsgleichgewicht — Gerechtigkeit und Wohlfahrt — Marktgleichgewichte bei unvollk. Konkurrenz — Anbieteranzahl und Kostenstruktur 3. Das Monopol: Monopolist. Preissetzung: Partialanalyse — Monopolmacht im allgemeinen Gleichgewicht — Das natürliche Monopol 4. Regulierung: Grenzkostenpreisbildung — Ramsey-Preise — Tarifgestaltung — Subvention — Ausschreibung eines natürlichen Monopols 5. Das Monopson und das bilaterale Monopol 6. Das Oligopol: Mengenwettbewerb nach Cournot — Preiswettbewerb nach Bertrand — Wettbewerbsbeschränkung: Kooperation Prof. Dr. Susanne Soretz Wettbewerb SS 2016 2 / 190 Literatur Bester, H. (2012), Theorie der Industrieökonomik, Springer. Binger, B. R., Hoffman, E. (1998) Microeconomics with Calculus, Addison Wesley. Borrmann, J., FinsingerJ. (1999) Markt und Regulierung, Vahlen. Henderson, J. M., Quandt, R. E. (1983) Mikroökonomische Theorie, Vahlen. Hey, J. D. (2003) Intermediate Microeconomics, McGrawHill. Linde, R. (1996), Mikroökonomie, Kohlhammer Verlag. Tirole, J. (1999), Industrieökonomik, Oldenbourg. Wied-Nebbeling, S., (2009) Preistheorie und Industrieökonomik, Springer. Wiese, H., (2010) Mikroökonomik, Springer. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 3 / 190 Organisatorisches Folien im Internet unter www.uni-greifswald.de/soretz/lehre/ Sprechstunden Mittwoch Nachmittag nach Vereinbarung, bitte per email anmelden: [email protected] Übung in 2 Gruppen (beginnt mit Außenwirtschaft und Konjunktur und Wachstum): siehe Übungsplan Prof. Dr. Susanne Soretz Wettbewerb SS 2016 4 / 190 Klausuren Scheinklausur für BWLer am Semesterende: 15. Juli 2016 um 08 Uhr s.t. im HS Loe Klausur für B.A.-Studenten: im Rahmen der AVWL Anfang September Vorkorrekturanträge bitte per email mit Angabe des Grundes (und Termins) bis zwei Wochen vor der betreffenden Klausur beantragen: z.B.: Vorkorrektur der AVWL wegen Fachmodulprüfung, Vorkorrektur AVWL wegen Auslandsbewerbung am 15.09. B.A.-Studenten, die ihre Fachmodulprüfung ablegen möchten, müssen sich innerhalb der kommenden Woche elektronisch melden!! mit Angabe der PO, des gewünschten Fachs, der noch fehlenden Vorleistungen, der Angabe ob Masterstudium Prof. Dr. Susanne Soretz Wettbewerb SS 2016 5 / 190 1 Einführung und Überblick: Warum Wettbewerb? Wettbewerb sichert Effizienz: das Marktergebnis ist pareto-optimal Preise komprimieren alle Informationen über die Knappheit der verschiedenen Güter Wettbewerb ist damit allen anderen Allokationsverfahren überlegen Prof. Dr. Susanne Soretz Wettbewerb SS 2016 6 / 190 Soziale Wohlfahrt aus der Herstellung eines Gutes: P X ➩ maximale soziale Wohlfahrt, wenn Grenznutzen = Grenzkosten. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 7 / 190 Koordination durch einen Wettbewerbsmarkt: P X Konsumenten erhöhen die Nachfrage, bis Preis = Grenznutzen Produzenten erhöhen das Angebot, bis Preis = Grenzkosten Marktgleichgewicht (Angebot = Nachfrage) bringt Grenznutzen und Grenzkosten in Übereinstimmung Das Gleichgewicht auf einem Wettbewerbsmarkt maximiert die soziale Wohlfahrt! Prof. Dr. Susanne Soretz Wettbewerb SS 2016 8 / 190 Der Fall vieler Güter und Produktionsfaktoren Es müssen nicht nur Nutzen und Kosten aus der Herstellung eines Gutes gegeneinander abgewogen werden, sondern auch die Produktionsmengen verschiedener Güter sowie die Aufteilung der Produktionsfaktoren auf die Sektoren. Besonders in einem solchen komplexen Umfeld sind Wettbewerbsmärkte allen anderen Allokationsverfahren überlegen. Sowohl Grenznutzen als auch Grenzkosten eines Gutes bzw. eines Produktionsfaktors hängen auch von der Verfügbarkeit anderer Güter bzw. Produktionsfaktoren ab. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 9 / 190 Beispiel: Der Nutzen von Skistiefeln ist größer, wenn mehr Skiurlaube gemacht werden. Der Grenznutzen steigt bzw. die Nachfrage verschiebt sich nach oben. Die optimale Skistiefelmenge steigt. P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 10 / 190 Beispiel: Die Herstellungskosten von Textilien steigen, wenn der Lohnsatz steigt. Die Grenzkosten steigen bzw. das Angebot verschiebt sich nach oben. Die optimale Menge Textilien sinkt. P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 11 / 190 2 Das allgemeine Gleichgewicht und das erste Wohlfahrtstheorem Quelle: Wiese (Kap. M) oder Henderson/Quandt (Kap. 9) Ziel: Herleitung des 1. Wohlfahrtstheorems: „Jedes Marktgleichgewicht ist Pareto-optimal“ Weg: Charakteristische Eigenschaften des Parto-Optimums finden; zeigen, dass diese Eigenschaften auch im Marktgleichgewicht erfüllt sind Prof. Dr. Susanne Soretz Wettbewerb SS 2016 12 / 190 Annahmen: Das 2x2x2-Modell es gibt zwei Individuen: a und b es gibt zwei Güter, Gut 1 und Gut 2 es gibt zwei Produktionsfaktoren: Arbeit L und Kapital K jeder Sektor produziert mit beiden Produktionsfaktoren gemäß X 1 = X 1 (L1 , K 1 ) bzw. X 2 = X 2 (L2 , K 2 ) (1) beide Produktionsfunktionen sind linear homogen (konstante Skalenerträge). die Produktionsfaktoren sind substituierbar, wobei die Grenzrate der technischen Substitution abnimmt (konvexe Isoquanten) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 13 / 190 2.1 Das Pareto–Optimum Bedingungen für Pareto–Optimalität: 1. Effiziente Produktion: Verteilung der Produktionsfaktoren auf die Sektoren: In keinem Sektor kann die Produktionsmenge erhöht werden, ohne dafür in einem anderen Sektor die Produktionsmenge zu senken. 2. Effizienter Verbrauch: Verteilung der Güter auf die Haushalte: Kein Haushalt kann mehr besser gestellt werden, ohne dafür einen anderen Haushalt schlechter zu stellen. 3. Effiziente Koordination von Produktion und Verbrauch: Produktionsmengen der Güter: Durch eine Änderung der Produktionsstruktur kann kein Haushalt mehr besser gestellt werden kann. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 14 / 190 Effiziente Produktion Isoquanten: K K L L Die Produktionsbedingungen legen die Form der Isoquanten fest: ➜ je leichter die Substitution, um so weniger gekrümmt sind die Isoquanten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 15 / 190 K L Steigung der Isoquanten: Grenzrate der technischen Substitution GRTS dX = 0 ➩ ➩ Prof. Dr. Susanne Soretz dK XL = GRTS = dL XK Wettbewerb SS 2016 (2) 16 / 190 Die Edgeworth–Box der Produktion: K1 L2 K2 L1 Effiziente Produktion Die Produktionsfaktoren sind effizient auf die Sektoren aufgeteilt, wenn die Grenzraten der technischen Substitution übereinstimmen. dK 1 dK 2 = ➩ GRTS 1 = GRTS 2 das heißt dL1 dL2 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 17 / 190 Die effiziente Produktion: ein Zahlenbeispiel So lange die Grenzraten der technischen Substitution verschieden sind, ist es möglich, in einem Sektor mehr zu produzieren, ohne in dem anderen Sektor weniger zu produzieren. Ausgangspunkt: Sowohl Arbeit als Kapital werden voll auch 2 1 1 1 beschäftigt. Die GRTS beträgt dK /dL = 5, die GRTS beträgt 2 dK /dL2 = 10. Erhöht man den Arbeitseinsatz in Sektor 2 um eine Einheit, kann man zehn Einheiten Kapital einsparen. Wenn man diese zehn Einheiten Kapital in Sektor 1 nutzt, werden zwei Einheiten Arbeit frei. Eine Einheit davon braucht man in Sektor 2, mit der anderen Einheit kann man mehr als in der Ausgangssituation produzieren. Erst wenn die GRTS in beiden Sektoren übereinstimmen, kann man durch eine Änderung der Produktionsstruktur keine Mehrproduktion mehr erreichen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 18 / 190 Die Transformationskurve Die Transformationskurve ist die grafische Darstellung aller effizienten Güterkombinationen. X2 K1 L2 K2 Prof. Dr. Susanne Soretz L1 Wettbewerb SS 2016 X1 19 / 190 Die Grenzrate der Transformation in der Regel ist die Transformationskurve konkav die Steigung der Transformationskurve heißt Grenzrate der Transformation GRT die GRT gibt an, auf wieviel Einheiten von Gut 2 verzichtet werden muss, um eine Einheit von Gut 1 mehr zu produzieren: Opportunitätskosten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 20 / 190 Opportunitätskosten und Grenzproduktivitäten: Die Grenzrate der Transformation misst die Opportunitätskosten von Gut 1: 2 dX (3) GRT = 1 dX Die Produktionsmengen verändern sich durch Veränderung des Faktoreinsatzes dX 1 = XL11 dL1 + XK1 1 dK 1 und dX 2 = XL22 dL2 + XK2 2 dK 2 Eine Bewegung auf der Transformationskurve erfolgt durch die Verlagerung von Produktionsfaktoren von Sektor 2 in Sektor 1, d. h. dL1 , dK 1 > 0 wobei dL1 = −dL2 Prof. Dr. Susanne Soretz und und dL2 , dK 2 < 0 dK 1 = −dK 2 Wettbewerb SS 2016 (4) (5) 21 / 190 so dass die GRT 2 dX dX 1 = ➩ GRT = XK2 2 XK1 1 (6) = XL22 (7) XL11 Die GRT entspricht bei effizienter Produktion dem Verhältnis der Grenzproduktivitäten von Arbeit bzw. Kapital. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 22 / 190 Effizienter Verbrauch Indifferenzkurven: X2 X2 X1 X1 Die Präferenzen bestimmen die Form der Indifferenzkurven: ➜ je besser die Güter substituierbar sind, um so weniger gekrümmt sind die Indifferenzkurven Prof. Dr. Susanne Soretz Wettbewerb SS 2016 23 / 190 X2 X1 Steigung der Indifferenzkurve: Grenzrate der Substitution GRS U = U(X 1 , X 2 ) ➩ dU = dU = 0 ➩ ➩ Prof. Dr. Susanne Soretz 2 dX U 1 GRS = 1 = X UX 2 dX Wettbewerb SS 2016 (8) 24 / 190 Die Edgeworth–Box des Verbrauchs: X 2a X 1b X 2b X 1a Effizienter Verbrauch Die Konsumgüter sind effizient auf die Haushalte verteilt, wenn die Grenzraten der Substitution übereinstimmen. ➩ GRS a = GRS b das heißt Prof. Dr. Susanne Soretz dX 2a dX 2b = dX 1a dX 1b Wettbewerb SS 2016 25 / 190 Effizienter Verbrauch: ein Zahlenbeispiel So lange die Grenzraten der Substitution verschieden sind, ist es möglich, einen Haushalt besser zu stellen, ohne den anderen Haushalt schlechter zu stellen. Ausgangspunkt: Sowohl Gut 1 als auch Gut 2 werden vollständig verbraucht. Die GRS a beträgt dX 2a /dX 1a = 2, die GRS b beträgt dX 2b /dX 1b = 1. Erhöht man den Konsum an Gut 1 von Haushalt a um eine Einheit, kann man seinen Konsum von Gut 2 um zwei Einheiten senken. Wenn man diese zwei Einheiten von Gut 2 nun Haushalt b gibt, dann werden zwei Einheiten des Gutes 1 frei. Eine Einheit davon braucht man, um Haushalt a so gut zu stellen wie zuvor, die andere Einheit kann zur Nutzensteigerung verwendet werden. Erst wenn die GRS beider Haushalte übereinstimmen, kann man durch eine Änderung der Verbrauchsstruktur keine Nutzensteigerung mehr erreichen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 26 / 190 Effiziente Koordination von Produktion und Verbrauch Produktionsmöglichkeiten ➩ Transformationskurve daraus resultierende Konsummöglichkeiten ➩ Edgeworth-Box des Verbrauchs X2 Effiziente Koordination von Produktion und Verbrauch Produktion und Verbrauch sind effizient koordiniert, wenn die Grenzraten der Substitution der Grenzrate der Transformation entsprechen ➩ GRT = GRS. X1 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 27 / 190 Effiziente Koordination von Produktion und Verbrauch: ein Zahlenbeispiel So lange die Grenzraten der Substitution von der GRT abweichen, ist es möglich, durch Änderung der Produktionsstruktur einen (beliebigen) Haushalt besser zu stellen. Ausgangspunkt: Sowohl Gut 1 als auch Gut 2 werden vollständig verbraucht. Die GRS a = GRS b = GRS beträgt dX 2 /dX 1 = 2, die GRT beträgt dX 2 /dX 1 = 1. Wird um eine Einheit mehr von Gut 1 produziert, kann um eine Einheit weniger von Gut 2 produziert werden. Die Haushalte verzichten aber auf zwei Einheiten von Gut 2, wenn sie eine Einheit mehr von Gut 1 bekommen. Die „übrige“ Einheit von Gut 2 kann somit nutzensteigernd verwendet werden. Erst wenn die GRS mit der GRT übereinstimmen, kann man durch eine Änderung der Produktionsmengen keine Nutzensteigerung mehr erreichen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 28 / 190 2.2 Das Wettbewerbsgleichgewicht Annahmen: vollkommener/vollständiger Wettbewerb: viele kleine Anbieter und Nachfrager auf allen Märkten ein homogenes Produkt je Markt kein technischer Fortschritt Annahmen: kein Marktversagen Rivalität im Konsum Anwendbarkeit des Ausschlussprinzips keine externen Effekte und Unteilbarkeiten ➜ Marktverhalten: Anbieter und Nachfrager sind Mengenanpasser/Preisnehmer Prof. Dr. Susanne Soretz Wettbewerb SS 2016 29 / 190 Die Faktormärkte Faktornachfrage gewinnmaximierender, mengenanpassender Unternehmen: max G1 = p 1 X 1 (K 1 , L1 ) − wL1 − rK 1 L1 ,K 1 ➩ XL11 XK1 1 = w r ➩ GRTS 1 = Faktorpreisverhältnis genauso: max G2 = p 2 X 2 (K 2 , L2 ) − wL2 − rK 2 L2 ,K 2 ➩ XL22 XK2 2 = w r Prof. Dr. Susanne Soretz ➩ GRTS 1 = GRTS 2 Wettbewerb SS 2016 (9) (10) (11) (12) 30 / 190 Faktornachfrage: w w L1 L2 ➜ Wenn sich alle Firmen an dem gleichen Faktorpreis orientieren, stimmen die jeweiligen Wertgrenzprodukte überein. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 31 / 190 noch einmal Faktornachfrage: K1 K2 L1 L2 ➜ Wenn sich alle Firmen an dem gleichen Faktorpreisverhältnis orientieren, stimmen die jeweiligen GRTS überein. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 32 / 190 Ergebnis: effizienzte Produktion Da sich alle Unternehmen am gleichen Faktorpreisverhältnis orientieren, stimmen alle GRTS überein. Faktorpreise bündeln alle relevanten Informationen über die Knappheit der Faktoren. Die Allokation der Produktionsfaktoren auf Wettbewerbsmärkten ist Pareto-optimal. Zentral dafür ist, dass alle Firmen den selben Faktorpreisen gegenüber stehen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 33 / 190 Die Gütermärkte Güternachfrage nutzenmaximierender, mengenanpassender Haushalte: max U a (X 1a , X 2a ) u. N.y a = p 1 X 1a + p 2 X 2a X 1a ,X 2a ➩ UXa 1a p1 = UXa 2a p2 Prof. Dr. Susanne Soretz (13) (14) Wettbewerb SS 2016 34 / 190 genauso: max U b (X 1b , X 2b ) u. N.y b = p 1 X 1b + p 2 X 2b X 1b ,X 2b ➩ ➩ UXb 1b UXb 2b = p1 p2 (15) GRS a = GRS b Prof. Dr. Susanne Soretz (16) Wettbewerb SS 2016 35 / 190 Güternachfrage: X 2a X 2b X 1a X 1b ➜ Wenn sich alle Haushalte an dem gleichen Güterpreisverhältnis orientieren, stimmen die jeweiligen GRS überein. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 36 / 190 Ergebnis: effizienter Konsum Da sich alle Haushalte am gleichen Güterpreisverhältnis orientieren, stimmen alle GRS überein. Die Güterpreise bündeln alle relevanten Informationen über die Knappheit der Güter. Der Verbrauch der Güter erfolgt auf Wettbewerbsmärkten Pareto-optimal. Zentral dafür ist, dass alle Haushalte den selben Güterpreisen gegenüber stehen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 37 / 190 Die Koordination von Produktion und Verbrauch Aus gewinnmaximierender und mengenanpassender Faktornachfrage der Unternehmen folgte (s.o.): p 1 XL11 = w = p 2 XL22 bzw. p 1 XK1 1 = r = p 2 XK2 2 Daraus bestimmt man die GRT im Marktgleichgewicht: 2 dX X 22 X 22 p1 GRT = 1 = L1 = K1 = 2 dX p X L1 XK 1 (17) (18) Aus nutzenmaximierender und mengenanpassender Güternachfrage der Haushalte folgte (s.o.): 2 dX p1 (19) GRS = 1 = GRS a = GRS b = 2 dX p Prof. Dr. Susanne Soretz Wettbewerb SS 2016 38 / 190 Zusammenfügen beider Bedingungen ergibt GRT = p1 = GRS p2 (20) Ergebnis: effiziente Koordination Da Produzenten und Konsumenten den selben Güterpreisen gegenüber stehen, stimmen GRT und GRS überein. Die Güterpreise vermitteln die Knappheit der Güter zwischen Produktion und Verbrauch. Die Koordination von Produktion und Verbrauch ist im Wettbewerbsgleichgewicht Pareto-optimal. Zentral dafür ist, dass Unternehmen und Haushalte den selben Güterpreisen gegenüber stehen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 39 / 190 Zusammenfassung Das erste Wohlfahrtstheorem: Unter der Bedingung vollständigen Wettbewerbs (sowie der Abwesenheit von Marktversagen) gilt: Jedes Marktgleichgewicht ist Pareto-optimal. Die Aufteilung der Produktionsfaktoren ist effizient (GRTS 1 = w /r = GRTS 2 ), da alle Unternehmen auf der Basis des gleichen Faktorpreisverhältnisses entscheiden. Die Aufteilung der Konsumgüter auf die Haushalte ist effizient (GRS a = p 1 /p 2 = GRS b ), da alle Haushalte auf der Basis des gleichen Güterpreisverhältnisses entscheiden. Die Koordination von Produktion und Verbrauch ist effizient (GRT = p 1 /p 2 = GRS), da Unternehmen und Haushalte auf der Basis des gleichen Güterpreisverhältnisses entscheiden. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 40 / 190 Die Preise erfüllen damit ihre Lenkungsfunktion, sie signalisieren die Knappheit von Produktionsfaktoren und Gütern. Die Preise können ihre Lenkungsfunktion nur erfüllen, wenn sie nicht verzerrt werden: bspw. verschiedene Mehrwertsteuersätze für verschiedene Güter; Wohngeld als Preissubvention für manche Haushalte; vergünstigter Kinoeintritt für Studenten; sozial gestaffelte Kindergartengebühren; geringere Ökosteuer für energieintensive Branchen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 41 / 190 2.3 Gerechtigkeit und Wohlfahrt Quelle: Linde Kap. 6.3 oder Hey Kap. 9 Wie gut geht es den beteiligten Haushalten in den jeweiligen Pareto-Optima? Es gibt Pareto-Optima, die wir als ungerecht empfinden, beispielsweise wenn Haushalt a nichts bekommt und Haushalt b alles. Gerechtigkeitsvorstellungen werden in sozialen Wohlfahrtsfunktionen erfasst, die Auskunft darüber geben, welches Pareto-Optimum sozial besser bewertet wird als welches andere. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 42 / 190 Wenn die Gütermengen vorgegeben sind, dann kann man aus der Kontraktkurve die zugehörigen Nutzenniveaus ableiten: Ub X 2a X 1b X 1a Ua Wettbewerb SS 2016 43 / 190 X 2b Prof. Dr. Susanne Soretz Auf der Basis gegebener Technologien und gegebener Faktormengen sind viele Güterkombinationen möglich (sh. Edgeworth-Box der Produktion). Entsprechend ist die Nutzenmöglichkeitenkurve die Umhüllende: Ub Ua Die Nutzenmöglichkeitenkurve gibt alle realisierbaren Kombinationen von Nutzenniveaus zweier Haushalte an. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 44 / 190 Die Nutzenmöglichkeitenkurve verläuft immer fallend: Der Nutzen eines Haushalts ist nur zu erhöhen, wenn dafür der Nutzen des anderen Haushalts gesenkt wird (andernfalls wäre die erste Situation nicht effizient gewesen). Genauere Aussagen über den Verlauf der Nutzenmöglichkeitenkurve sind ohne weiteren Annahmen über die Präferenzen nicht möglich. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 45 / 190 Welcher Punkt auf der Nutzenmöglichkeitenkurve soll realisiert werden? ➩ Welche Nutzenverteilung ist gerecht? Gerechtigkeit hat immer etwas mit Gleichheit zu tun, es gibt aber sehr verschiedene Ansichten, was gleich sein soll: Startgerechtigkeit: gleiche Anfangsausstattung aller Haushalte Leistungsgerechtigkeit: gleiches Einkommen bei gleicher Leistung Regelgerechtigkeit: auf alle Wirtschaftssubjekte sollen die gleichen Regeln angewendet werden Ergebnisgerechtigkeit: gleiche Güterausstattung (oder gleiche Nutzenniveaus) für alle Haushalte Prof. Dr. Susanne Soretz Wettbewerb SS 2016 46 / 190 Wohlfahrtsfunktionen Die Überlegungen bezüglich sozialer Gerechtigkeit werden in der Regel in Form von sozialen Wohlfahrtsfunktionen zusammengefasst: Soziale Wohlfahrtsfunktion: Eine soziale Wohlfahrtsfunktion gibt an, welche Größen für das Wohlergehen einer Gesellschaft (eines Landes) maßgeblich sind und in welcher Weise das gesellschaftliche Wohlfahrtsniveau von ihnen abhängt. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 47 / 190 Zwei verschiedene Ansätze: Leontief-Lerner und Bergsson Die Leontief-Lerner-Wohlfahrtsfunktion unterstellt, dass das Wohlergehen einer Gesellschaft von der Menge an Gütern abhängt, die ihr zur Verfügung stehen (und nicht von der Verteilung der Güter auf die Individuen): W = W (X 1 , ...X n ) (21) Die Bergsson-Wohlfahrtsfunktion unterstellt, dass das Wohlergehen einer Gesellschaft von den Nutzenniveaus der Individuen abhängt: W = W (U a , ...U m ) Prof. Dr. Susanne Soretz (22) Wettbewerb SS 2016 48 / 190 Leontief-Lerner-Wohlfahrtsfunktion: X2 X1 Die Leontief-Lerner-Wohlfahtsfunktion wird beispielsweise in der Außenhandelstheorie viel benutzt. Für die Indifferenzkurven wird die übliche konvexe Gestalt angenommen. Sie macht keine Aussagen über die gesellschaftlichen Konsequenzen der Verteilung. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 49 / 190 Bergsson-Wohlfahrtsfunktionen: Ub Ua Die Gruppe der Bergsson-Wohlfahrtsfunktionen lässt sich weiter unterteilen, je nach dem, wie groß die Ungleichheitsaversion der Gesellschaft ist: Konvexe Indifferenzkurven zeigen Ungleichheitsaversion. Weniger ungleiche Nutzenverteilungen führen zu Punkten auf höher gelegenen Indifferenzkurven. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 50 / 190 Die Wohlfahrtsfunktion nach Rawls: W = min[U 1 , ..., U m ] Ub Ua Die gesellschaftliche Wohlfahrt hängt ausschließlich von dem Nutzen des am schlechtesten gestellten Mitglieds der Gesellschaft ab. Die Wohlfahrtsfunktion nach Rawls impliziert unendliche Ungleichheitsaversion. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 51 / 190 j Die Wohlfahrtsfunktion nach Bentham: W = ∑m j=1 U Ub Ua Die gesellschaftliche Wohlfahrt kann durch die Summe der individuellen Nutzenniveaus dargestellt werden. Die Senkung des Nutzens eines Haushalts kann durch eine gleich große Erhöhung des Nutzens eines anderen Haushalts ausgeglichen werden. Selbst Umverteilung von Armen zu Reichen ist wohlfahrtsneutral möglich: Es gibt keine Ungleichheitsaversion Prof. Dr. Susanne Soretz Wettbewerb SS 2016 52 / 190 Die Wohlfahrtsfunktion nach Nash: W = (U 1 − U¯1 ) · . . . · (U m − U¯m ) Ub Ua Die gesellschaftliche Wohlfahrt hängt multiplikativ von den Überschüssen der individuellen Nutzen über gewisse Mindestnutzenniveaus ab. Für niedrige Nutzenniveaus sind die Indifferenzkurven stark gekrümmt (hohe Ungleichheitsaversion), mit steigenden Nutzenniveaus werden die Indifferenzkurven weniger gekrümmt, die Ungleichheitsaversion nimmt ab. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 53 / 190 Das gesellschaftliche Wohlfahrtsmaximum Ub Ua Nur Punkte auf der Nutzenmöglichkeitenkurve (d. h. nur effiziente Punkte) können ein Wohlfahrtsmaximum sein. ➩ 1. Schritt: Herstellung von Effizienz Der wohlfahrtsmaximierende Punkt ist der Tangentialpunkt von Nutzenmöglichkeitenkurve und Indifferenzkurve. ➩ 2. Schritt: Herstellung von Verteilungsgerechtigkeit Prof. Dr. Susanne Soretz Wettbewerb SS 2016 54 / 190 und warum das Wohlfahrtsmaximum i.d.R. nicht bestimmbar ist: „Die richtige“ soziale Wohlfahrtsfunktion ist im Allgemeinen nicht festzulegen, denn: Die Mitglieder einer Gesellschaft haben verschiedene Ansichten über soziale Wohlfahrtsfunktion, bspw. die Ungleichheitsaversion, aber auch über die relevanten Variablen. Unmöglichkeitstheorem von Arrow: Konsistente (aber verschiedene) individuelle Präferenzen lassen sich nicht widerspruchsfrei zu einer konsistenten gesellschaftlichen Wohlfahrtsfunktion aggregieren. ➜ deshalb nutzen wir die Effizienz des Wettbewerbs (Pareto-Kriterium) und ergänzen um sozialpolitische Maßnahmen (Umverteilung, sozialer Ausgleich) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 55 / 190 Wettbewerb — Neoliberalismus — Marktradikalismus? Liberalismus (liberalis = freiheitlich) ist im 17. Jahrhundert entstanden zunächst insbesondere als Gegenbewegung zu Ungleichheit der Menschen: Fürsten, Könige, Leibeigene... Merkantilismus: strikte Regelung der Wirtschaft durch Könige bzw. Fürsten, vor allem Exportförderung zur Generierung von Staatseinnahmen und Importbeschränkung durch Zölle, keine Berufsfreiheit Kameralismus: Fürsten organisierten die Wirtschaft so, dass ihre Einnahmen maximiert wurden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 56 / 190 wichtige Wegbereiter: John Locke (1632–1704) Philosoph früher Wegbereiter der Aufklärung Adam Smith (1723 – 1790) Moralphilosoph, Begründer der klassischen Nationalökonomie ➜ Wealth of Nations ➜ unsichtbare Hand John Stuart Mill (1806 – 1873) Philosoph und Nationalökonom Utilitarismus ➜ wichtig ist wie gut es den Menschen geht (nicht die Macht der Nation) ➜ forderte Bildung, Gleichberechtigung, Erbschaftssteuer Prof. Dr. Susanne Soretz Wettbewerb SS 2016 57 / 190 Liberalismus jeder Einzelne darf selbst bestimmen, was er produziert und wem er es verkauft bedeutet nicht ungezügelten Egoismus, sondern vor allem Nutzung der Wettbewerbskräfte statt Interventionismus selbstverständlich gibt es Grenzen, beispielsweise durch Gesetze es soll der Gesellschaft möglichst gut gehen (Utilitarismus ➜ dafür muss es den Bürgern möglichst gut gehen) freiheitliches Weltbild und unsichtbare Hand ➜ Privateigentum; Wettbewerb als Koordinationsmechanismus die Weltwirtschaftskrise und die große Rezession zeigten die Grenzen der reinen Marktkräfte Prof. Dr. Susanne Soretz Wettbewerb SS 2016 58 / 190 Gegenbewegung: Keynesianismus John Maynard Keynes (1883 – 1946) Mathematiker und Ökonom (und Philosoph und Historiker, mathematische Dissertation) propagierte nach Weltwirtschaftskrise und Deflation nachfrageorientierte Wirtschaftspolitik Keynesianismus Staat soll Nachfragerückgang der privaten Haushalte ausgleichen Marktwirtschaft kann sich nicht alleine aus Deflation befreien: sinkende Löhne ➜ sinkende Nachfrage ➜ sinkende Unternehmensgewinne ➜ sinkende Löhne Prof. Dr. Susanne Soretz Wettbewerb SS 2016 59 / 190 Reaktion auf Keynesianismus: Neoliberalismus Chicagoer Schule wichtig: Milton Friedman, Nobelpreis 1976 betonen besonders stark die Nachteile von Staatseingriffen Österreichische Schule wichtig: Friedrich von Hayek, Nobelpreis 1974 heben Ungleichgewichte und Anpassungsprozesse an Gleichgewichte hervor (Keynes’sche Unterkonsumption unglaubwürdig) Ordoliberalismus (ordo (lat.) = Ordnung) wichtig: Walter Eucken der Staat gibt den Ordnungsrahmen vor für den freien Wettbewerb Prof. Dr. Susanne Soretz Wettbewerb SS 2016 60 / 190 in Deutschland: Soziale Marktwirtschaft Ludwig Erhard (1897 – 1977) Wirtschaftswissenschaftler deutscher Wirtschaftsminister 1949 – 1963 (danach Bundeskanzler) gilt als Vater des Wirtschaftswunders und der Sozialen Marktwirtschaft Soziale Marktwirtschaft soll „auf der Basis der Wettbewerbswirtschaft die freie Initiative mit einem gerade durch die wirtschaftliche Leistung gesicherten sozialen Fortschritt verbinden“ (Müller-Armack) entstanden im Weltbild des Ordoliberalismus aber stärkere soziale Komponente (nach Entwickler Müller-Armack und auf Betreiben Adenauers) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 61 / 190 Zusammenfassung: freie Entscheidung des Einzelnen und Koordination durch Märkte erfüllen unsere Vorstellung einer freiheitlichen Grundordnung Marktgleichgewicht ist Pareto-effizient (sh. erstes Wohlfahrtstheorem), aber erfüllt nicht unsere Vorstellungen von Gerechtigkeit deshalb wird umverteilt ➜ soziale Marktwirtschaft dabei entsteht ein Zielkonflikt zwischen Effizienz und Gerechtigkeit (equity-efficiency trade off) heute geht es bei „Neoliberalismus“-Diskussion primär um: ➜ wie viel Umverteilung empfinden wir als gerecht? ➜ wie wägen wir die Nachteile von Staatseingriffen gegen die Nachteile der ungerechten Marktergebnisse ab? Prof. Dr. Susanne Soretz Wettbewerb SS 2016 62 / 190 2.4 Überblick: Marktgleichgewichte bei unvollkommener Konkurrenz Quelle: Wied-Nebbeling (Kap. I) Marktergebnisse in der Realität sind nicht immer Pareto–optimal: es gibt Marktversagen ➜ Ursachen: Gütereigenschaften wie Nichtrivalität im Konsum (Leuchtturm) oder mangelnde Ausschließbarkeit (Straßennetz) ➜ Behandlung in Finanzwissenschaft externe Effekte (Umweltverschmutzung) ➜ Behandlung in Umweltökonomie (und Finanzwissenschaft) Marktmacht: Unternehmen verhalten sich dann nicht mehr mengenanpassend (Oligopol auf dem Strommarkt) ➜ Thema hier im Folgenden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 63 / 190 Die Marktstruktur: das morphologische Marktformenschema Die Marktstruktur hängt wesentlich davon ab, wie viele Marktteilnehmer es auf den beiden Marktseiten gibt: Nachfrager einer bilaterales Monopol beschränktes wenige Monopson beschränktes Monopol bilaterales Oligopol viele Oligopson einer Anbieter wenige Prof. Dr. Susanne Soretz Monopson Wettbewerb SS 2016 viele Monopol Oligopol Polypol 64 / 190 Relativierung des Marktformenschemas Contestable Markets nach Baumol/Panzar/Willig (1982): Nicht alleine die Anzahl der auf dem Markt befindlichen Unternehmen entscheidet über deren Verhalten. Genau so wichtig ist der potentielle Wettbewerb. Ist der Marktzugang frei und der Marktaustritt kostenlos, dann ist der Markt bestreitbar und hohe Marktanteile führen nicht zu Preissetzungsspielraum. In der Realität überwiegen jedoch Märkte mit beschränktem Zugang. Abgrenzung wenige versus viele Anbieter: Abgrenzung erfolgt in der Regel über die Spürbarkeit der Aktionen einzelner Anbieter für die Mitkonkurrenten. Die Resultate sind aber nicht immer eindeutig. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 65 / 190 Abgrenzung des Marktes: Für die Anzahl der Marktteilnehmer ist der relevante Markt entscheidend (Bsp.: Markt für Werbung auf Litfaßsäulen, Markt für Werbung in allen Medien). Kriterium für den relevanten Markt sind die Substitutionsmöglichkeiten, gemessen anhand der Kreuzpreiselastizität ηX 1 ,P 2 = Prof. Dr. Susanne Soretz dX 1 /X 1 dP 2 /P 2 Wettbewerb SS 2016 66 / 190 2.5 Anbieteranzahl und Kostenstruktur Mengenanpassende Unternehmen: max G(x) = Px − C(x) x (23) ➩ x ➜ individuelle Angebotsfunktion entspricht GK -Funktion aggregiertes Angebot = Anbieteranzahl × individuelles Angebot Prof. Dr. Susanne Soretz Wettbewerb SS 2016 67 / 190 Kurzfristiges versus langfristiges Marktgleichgewicht: P X (kurzfristiges) Marktgleichgewicht: Preis und Menge konstant verändert sich die Anbieteranzahl, dann verlagert sich die Angebotsfunktion ➜ dann passen sich Preis und Menge im Marktgleichgewicht an Prof. Dr. Susanne Soretz Wettbewerb SS 2016 68 / 190 positive Gewinne ➜ Markteintritte ➜ Anbieteranzahl steigt negative Gewinne ➜ Marktaustritte ➜ Anbieteranzahl sinkt langfristiges Marktgleichgewicht: Im langfristigen Marktgleichgewicht bleibt die Anbieteranzahl konstant. Dafür müssen die Gewinne null sein ➜ Nullgewinnbedingung. Wann sind die Gewinne null? G≷0 ⇐⇒ ⇐⇒ P ≷ DK (24) Zwischenfazit: Gewinnmaximierung ➜ P = GK Gewinne versus Verluste ➜ P ≷ DK Prof. Dr. Susanne Soretz Wettbewerb SS 2016 69 / 190 Beziehung zwischen Grenzkosten und Durchschnittskosten: x normal: steigende Grenzkosten, Fixkosten DK sind bei geringer Menge groß (Fixkosten) und sinken zunächst (Fixkostendegression), später dominieren die steigenden GK ➜ U-förmige DK DK sinken, solange GK < DK und steigen, sobald GK > DK ➜ die GK schneiden die DK in deren Minimum Prof. Dr. Susanne Soretz Wettbewerb SS 2016 70 / 190 Maximal realisierbarer Gewinn: x Angebot gemäß GK -Funktion ➜ positiver Gewinn, falls P > DK ➜ Markteintritte ➜ Angebotsfunktion verlagert sich nach rechts ➜ Preis sinkt ➜ Gewinn sinkt ➜ Verlust, falls P < DK ➜ Marktaustritte ➜ Angebotsfunktion verlagert sich nach links ➜ Preis steigt ➜ Gewinn steigt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 71 / 190 langfristiges Marktgleichgewicht: P x X sei am Anfang n gering ➜ Preis hoch ➜ Gewinne ➜ Markteintritte Preis sinkt so lange bis P = DK und damit Nullgewinne erst dann Anbieteranzahl konstant ➜ Preis und Menge konstant ➜ langfristig produziert das einzelne Unternehmen im Minimum der DK und die Anbieteranzahl ergibt sich aus n∗ x ∗ = X ∗ Prof. Dr. Susanne Soretz Wettbewerb SS 2016 72 / 190 Zusammenfassung Marktgröße: die Anbieteranzahl ist nur konstant, wenn der Preis den Durchschnittskosten entspricht Mengenanpasser wählen ihre Angebotsmenge immer so, dass der Preis den Grenzkosten entspricht Nullgewinne und Gewinnmaximierung gleichzeitig sind nur möglich, wenn Durchschnittskosten und Grenzkosten übereinstimmen langfristig produziert jedes Unternehmen im Minimum der Durchschnittskosten ➜ die Anbieteranzahl hängt davon ab, wievielfach die Nachfragemenge die individuelle Produktionsmenge übersteigt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 73 / 190 ➜ je höher die Fixkosten, um so größer die Produktionsmenge, bei der die Durchschnittskosten minimal sind ➜ um so weniger Anbieter im langfristigen Marktgleichgewicht (wenige Flugzeugproduzenten, aber viele Friseure) ➜ je größer die Nachfrage, um so mehr Unternehmen können kostendeckend in dem Markt anbieten (wenige Panzerproduzenten, aber viele Bäcker) P P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 X 74 / 190 3 Das Monopol Quelle: Wied-Nebbeling (Kap. II.1) und Tirole (Kap. 1.1.1, 10.1) Der Monopolist nutzt seine Marktmacht, um das Marktergebnis zu seinen Gunsten zu verändern: In der Regel setzt er einen höheren Preis, so dass die konsumierte Menge sinkt. Dadurch entstehen Wohlfahrtsverluste. Der soziale Überschuss auf dem betroffenen Markt sinkt. Es wird suboptimal wenig in dem monopolisierten Sektor produziert, und dadurch subpotimal viel in den anderen Sektoren. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 75 / 190 Einschränkung: Der untersuchte Fall des sogenannten reinen Monopols ist realitätsfern. Die Marktmacht ist beschränkt, wenn es Substitute gibt oder der Markt bestreitbar ist. Die Marktmacht kann auch zeitlich beschränkt sein, wenn neue Anbieter in den Markt kommen, bspw. weil Patente auslaufen oder wegen der Monopolgewinne. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 76 / 190 3.1 Monopolistische Preissetzung: Partialanalyse Der Monopolist maximiert seinen Gewinn max G = PX (P) − C(X (P)) P ➩ ∂G = ∂P ➩ 1 PM − C′ =− M η p Prof. Dr. Susanne Soretz prozentualer Preisaufschlag Monopolgrad nach Lerner Wettbewerb SS 2016 (25) 77 / 190 Mengensetzung führt zum gleichen Gewinnmaximum max G = P(X )X − C(X ) X ➩ ∂G = ∂X ➩ 1 PM − C′ =− M η p ➩ preissetzende und mengensetzende Monopolisten erheben den gleichen Preisaufschlag und realisieren beide den Cournot’schen Punkt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 78 / 190 Die Marktmacht des Monopolisten: Erhöht der Monopolist den Preis, dann bekommt er für jede verkaufte Einheit etwas mehr (positiver Bestandteil X aus dem Grenzerlös). Andererseits sinkt die nachgefragte Menge, so dass der Monopolist weniger Einheiten verkaufen kann als vorher (negativer Bestandteil PXP ). Je elastischer die Nachfrage, um so stärker sinkt die nachgefragte Menge. Die Monopolmacht und damit der relative Preisaufschlag sind um so größer, je unelastischer die Nachfrage ist, da sich Preisaufschläge dann leichter durchsetzen lassen. (Bspw. relativ geringe Preiselastizität des Energieverbrauchs ➩ große Marktmacht der Energieversorger.) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 79 / 190 Statische Ineffizienz durch Marktmacht P X ! Das Gewinnmaximum impliziert GE = GK ➩ Angebot im Cournot’schen Punkt. ! Für das Wohlfahrtsmaximum gilt Preis = Grenzkosten. Es entsteht ein Wohlfahrtsverlust aus dem monopolistischen Preisaufschlag: Harberger Dreieck oder Dead-Weight Loss. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 80 / 190 Wird außerdem ineffizient produziert? Monopolist würde trotz höherer Kosten nicht vom Markt verdrängt aber: sein Gewinn würde sinken! ➜ auch Monopolisten produzieren zu minimalen Kosten Sind Eigentumsebene (Aktionäre) und Entscheidungsebene (Management) getrennt, hat das Management vielleicht andere Ziele neben der Gewinnmaximierung ➜ dann ist ein Monopolist schwerer zu kontrollieren als ein Konkurrenzunternehmen ➜ bei Monopolen wird eher sog. X-Ineffizienz auftreten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 81 / 190 falls ineffiziente Produktion, zusätzlicher Wohlfahrtsverlust: P X bei höheren GK sinkt die Menge und steigt der Preis weiter WFV steigt noch über den Wohlfahrtsverlust gemäß Harberger Dreieck hinaus Prof. Dr. Susanne Soretz Wettbewerb SS 2016 82 / 190 Dynamische Ineffizienz durch Marktmacht Kernproblem: technischer Fortschritt reduziert bspw. Produktionskosten oder erhöht die Produktqualität, aber es erfordert Aufwand, technischen Fortschritt zu erreichen (Forschungsabteilung) Monopole sind oft wenig innovativ (Bsp. Deutsche Bahn) Grund: geringere Anreize zu Innovationen im Monopol, da sich die Kostenreduktion nur auf eine geringere Stückzahl auswirkt; außerdem keine Gefahr, durch innovative Konkurrenz aus dem Markt vertrieben zu werden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 83 / 190 Referenzsituation „soziales Optimum“: Wann sollte eine Innovation durchgeführt werden? P X sinken die Grenzkosten von c̄ auf c, dann steigt die Wohlfahrt um R c̄ D ∗ ∗ WFG = c X (P (c))dc ➜ Innovation durchzuführen ist sinnvoll, wenn die Kosten der Innovation geringer als WFG∗ sind Prof. Dr. Susanne Soretz Wettbewerb SS 2016 84 / 190 Konkurrenzgleichgewicht: P X KR steigt um gleiche Fläche wie WFG∗ im sozialen Optimum, Konsumenten würden Innovation befürworten aber Gewinne der Unternehmen bleiben null, also können Kosten der Innovation sich nicht amortisieren ➜ Innovation wird nicht durchgeführt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 85 / 190 Konkurrenzgleichgewicht mit Patentschutz: ➩ innovatives Unternehmen ist das einzige, das über die neue Technologie verfügt P falls Cournot’scher Preis größer als c̄: inkrementelle Innovation X Erfinder unterbietet die anderen infinitesimal ➜ setzt gesamte Menge X D (c̄) ab ➜ Gewinnsteigerung aus Innovation ist: GK = (c̄ − c)X D (c̄) < WFG∗ Innovation lohnt sich nur, wenn Kosten < GK ➜ falls GK < Kosten < WFG∗ , wäre Innovation sinnvoll, wird aber nicht durchgeführt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 86 / 190 Konkurrenzgleichgewicht mit Patentschutz: P falls Cournot’scher Preis kleiner als c̄: drastische Innovation X Erfinder setzt Monopolpreis P M < c̄ ➜ verkauft Monopolmenge X D (P M ) ➜ Gewinnsteigerung aus Innovation ist GK = (P M − c)X D (P M ) < WFG∗ Innovationsanreiz wieder kleiner als im sozialen Optimum ➜ falls GK < Kosten < WFG∗ , wäre Innovation sinnvoll, wird aber nicht durchgeführt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 87 / 190 Monopolist: P X gewinnmaximierender Preis sinkt durch Innovation, Absatzmenge steigt, Gewinn steigt wie viel genau steigt der Gewinn? ➜ entscheidend für den Innovationsanreiz des Monopolisten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 88 / 190 Veränderung des optimalen Gewinns mit den Grenzkosten: d ((P M∗ − c)X D (P M∗ )) dGM = dc dc ∂ (P M∗ − c)X D (P M∗ ) ∂ (P M∗ − c)X D (P M∗ ) ∂ P M∗ = + M∗ ∂{zc ∂P } | | {z } ∂c =0 im Opt. =−X D (P M∗ ) D = −X (P M∗ ) (26) Gewinnsteigerung aus Innovation ist: ∆GM = GM (P M (c)) − GM (P M (c̄)) = = Z c̄ c X D (P M∗ ) dc Prof. Dr. Susanne Soretz (27) Wettbewerb SS 2016 89 / 190 P X Monopolist führt Innovation durch, wenn die Kosten der Innovation geringer sind als ∆GM < GK < WFG∗ Innovationsanreiz des Monopolisten ist ebenfalls zu klein, es gibt also sozial wünschenswerte Innovationen, die nicht durchgeführt werden. falls ∆GM < Kosten < WFG∗ , wäre Innovation sinnvoll, wird aber nicht durchgeführt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 90 / 190 Ergebnisse: im Konkurrenzgleichgewicht ohne Patentschutz fehlt der Innovationsanreiz völlig im Konkurrenzgleichgewicht mit Patentschutz ist der Innovationsanreiz zu gering (GK < WFG): da eine suboptimal geringe Menge produziert wird, sind die Auswirkungen der Kostensenkung zu gering im Monopol ist der Innovationsanreiz noch geringer als im Konkurrenzgleichgewicht mit Patentschutz (∆GM < GK ) bei Konkurrenz profitieren Unternehmen davon, durch Innovation Marktanteile zu gewinnen Monopolist profitiert aber nur von Absatzsteigerung durch sinkenden Preis: „ersetzt sich selbst“ ➜ replacement effect (Arrow) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 91 / 190 Die Preissetzung des Mehrproduktmonopolisten Ein Monopolist, der zwei Güter anbietet, maximiert seinen Gewinn: max G =P 1 X 1 (P 1 , P 2 ) + P 2 X 2 (P 1 , P 2 ) P 1 ,P 2 − C(X 1 (P 1 , P 2 ), X 2 (P 1 , P 2 )) ∂G = ∂ P1 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 92 / 190 ➩ ′ XP21 P1 − C1 1 2 2′ = − − (P − C ) P1 η1 P 1 XP11 analog ➩ (28) ∂G ! =0 ∂ P2 ′ XP12 P2 − C2 1 1 1′ = − − (P − C ) P2 η2 P 2 XP22 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 (29) 93 / 190 entscheidend ist die Beziehung zwischen den beiden Gütern: Sind die Güter substitutiv, dann ist die Kreuzableitung positiv ∂X2 > 0 und ∂ P1 ∂X1 >0 ∂ P2 (30) da die Nachfrage nach Gut 2 (Gut 1) steigt, wenn der Preis des Gutes 1 (des Gutes 2) zunimmt. Sind die Güter komplementär, dann ist die Kreuzableitung negativ ∂X2 < 0 und ∂ P1 ∂X1 <0 ∂ P2 (31) da die Nachfrage nach Gut 2 (Gut 1) sinkt, wenn der Preis des Gutes 1 (des Gutes 2) zunimmt. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 94 / 190 Preissetzung bei substitutiven Gütern (XP21 > 0): Der Mehrproduktmonopolist erhebt in beiden Sektoren einen höheren (prozentualen) Aufschlag auf die Grenzkosten als ein Monopolist, der nur Sektor 1 oder nur Sektor 2 beliefert. Der Mehrproduktmonopolist nutzt aus, dass er beide Preise gleichzeitig anheben kann und damit den Konsumenten die Möglichkeit nimmt, auf das günstigere Gut auszuweichen. Die Marktmacht des Monopolisten steigt, wenn er nicht nur einen Markt, sondern weitere Märkte für substitutive Güter kontrolliert (Bsp.: (frühere) lokale Energieversorger, die frühere Post). Prof. Dr. Susanne Soretz Wettbewerb SS 2016 95 / 190 Preissetzung bei komplementären Gütern (XP21 < 0): Der Mehrproduktmonopolist erhebt in beiden Sektoren einen kleineren (prozentualen) Aufschlag auf die Grenzkosten als ein Monopolist, der nur Sektor 1 oder nur Sektor 2 beliefert. Durch Preiserhöhungen auf einem Markt verschlechtern sich die Gewinnmöglichkeiten auf dem anderen Markt. Wenn der Monopolist von der Verschlechterung selbst getroffen wird, senkt das seinen Preisaufschlag. Hier spürt der Monopolist einen Teil der verzerrenden Wirkung seiner Preissetzung selbst auf dem zweiten Markt, so dass sich sein Preissetzungsspielraum verringert. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 96 / 190 3.2 Monopolmacht im allgemeinen Gleichgewicht Monopolisten nutzen ihre Marktmacht, um den Preis zu erhöhen und dadurch ihren Gewinn zu steigern. Inwieweit ist das allgemeine Gleichgewicht verzerrt? Wird in der Ökonomie insgesamt „zu wenig“ produziert, das heißt weniger als bei effizientem Faktoreinsatz produziert werden könnte? Wir werden zeigen, dass auch Monopolisten wegen ihrer Gewinnerzielungsabsicht effizient produzieren. Somit ist die Faktorallokation trotz Marktmacht effizient (Produktion auf der Transformationskurve). Aber die Abstimmung zwischen Produktion und Konsum ist ineffizient, so lange nicht alle Märkte den gleichen Monopolgrad aufweisen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 97 / 190 Effiziente Produktion? Faktornachfrage des Monopolisten in Sektor 1: max G1 = P 1 (X 1 (K 1 , L1 )) · X 1 (K 1 , L1 ) − rK 1 − wL1 K 1 ,L1 ➩ (32) ∂ G1 = ∂K1 (33) ∂ G1 = ∂ L1 (34) (35) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 98 / 190 r w K1 L1 ➜ Monopolist produziert weniger als Mengenanpasser ➜ dafür benötigt er weniger Kapital bzw. Arbeit Prof. Dr. Susanne Soretz Wettbewerb SS 2016 99 / 190 ➩ GRTS 1 = = XL11 XK1 1 (36) = w r (37) genauso für den Monopolist in Sektor 2: ➩ 2 GRTS = Prof. Dr. Susanne Soretz XL22 XK2 2 = w r ➩ GRTS 1 = GRTS 2 Wettbewerb SS 2016 (38) 100 / 190 X2 K1 L2 K2 L1 X1 Ergebnis: effiziente Produktion (Gütermarkt-)Monopolisten sind Mengenanpasser auf den Faktormärkten sie sind mit dem gleichen Faktorpreisverhältnis konfrontiert ineffiziente Produktion (GRTS 6= w /r ) würde den Gewinn des Monopolisten reduzieren es werden Produktionspunkte auf der Kontraktkurve und entsprechend auf der Transformationskurve realisiert Prof. Dr. Susanne Soretz Wettbewerb SS 2016 101 / 190 Effizienter Verbrauch? Haushalte sind Mengenanpasser und maximieren ihren Nutzen ➩ Marktergebnis wie bei vollkommenem Wettbewerb: GRS a = GRS b = p1 p2 (39) Ergebnis: effizienter Verbrauch Haushalte sind Mengenanpasser auf den Gütermärkten. Auch bei Monopolmacht werden Konsumpunkte auf der Kontraktkurve realisiert. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 102 / 190 Effiziente Koordination von Produktion und Verbrauch? Die Grenzrate der Transformation: 2 dX X 22 X 22 GRT = 1 = L1 = K1 dX X L1 XK 1 p 1 1 + η11 ➩ GRT = p 2 1 + η12 (40) (41) Die Grenzrate der Substitution: GRS a = GRS b = GRS = Prof. Dr. Susanne Soretz p1 p2 Wettbewerb SS 2016 (42) 103 / 190 Übereinstimmung von GRT und GRS? p 1 1 + η11 ?? p 1 = 2 p p2 1 + 1 (43) η2 Wenn die Monopolgrade 1/η i nicht genau übereinstimmen — oder wenn nur ein Sektor monopolisiert ist — dann unterscheidet sich die Grenzrate der Transformation von der Grenzrate der Substitution. Beispiel: Monopol nur in Sektor 1 p 1 1 + η11 p1 < p2 p2 (44) Die GRT ist kleiner als die GRS, die Koordination von Produktion und Verbrauch ist ineffizient. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 104 / 190 Monopol nur in Sektor 1: X2 X1 Ergebnis: keine effiziente Koordination von Produktion und Verbrauch der Produktionspunkt liegt auf der Transformationskurve, jedoch ist die GRT kleiner als die GRS es wäre eine Pareto–Verbesserung, wenn mehr von Gut 1 und dafür weniger von Gut 2 produziert würde Prof. Dr. Susanne Soretz Wettbewerb SS 2016 105 / 190 3.3 Das natürliche Monopol Bei steigenden Kosten ist das Monopol keine stabile Marktform. Langfristig werden zusätzliche Anbieter in den Markt drängen. Dies senkt die Produktionskosten für alle Anbieter. Anders ist das bei sinkenden Kosten. In diesem Fall sind die Kosten am geringsten, wenn nur ein Unternehmen den gesamten Markt bedient. Zentrale Ursachen sind Unteilbarkeiten und Netzeffekte. (Beispiele: Elektrizitätsnetze, Müllabfuhr, Postzustellung) Ein Monopol ist dann gesellschaftlich wünschenswert. Und es ist eine stabile Marktform: Deshalb nennt man diesen Fall das natürliche Monopol. Trotzdem muss die monopolistische Preissetzung verhindert werden, um keine Wohlfahrtseinbußen zu erleiden. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 106 / 190 Subadditivität Eine Kostenfunktion ist subadditiv, wenn die Herstellung einer bestimmten Produktionsmenge in nur einer Produktionsstätte kostengünstiger ist als die Herstellung in zwei (oder mehr) Produktionsstätten: C(X ) < C(X1 ) + . . . + C(Xn ) mit X = X1 + . . . + Xn (45) Subadditivität tritt im Wesentlichen in zwei Fällen auf: bei steigenden Skalenerträgen bei Fixkosten (Unteilbarkeiten) In jedem Fall ist davon auszugehen, dass bei hinreichend hoher Produktionsmenge die Kosten wieder steigen. ➩ Ein natürliches Monopol liegt vor, wenn die Kostenstruktur im relevanten Bereich subadditiv ist. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 107 / 190 Skalenvorteile Im Einproduktunternehmen liegen Skaleneffekte vor, wenn bei einer Mengenerhöhung die Kosten nur unterproportional steigen, d. h. wenn die Kostenelastizität kleiner als 1 ist: ηC,X = dC/C <1 dX /X (46) Daraus folgen sinkende Durchschnittskosten: ηC,X < 1 ➩ d (C/X ) <0 dX (47) und Durchschnittskosten, die über den Grenzkosten liegen: ηC,X < 1 ➩ Prof. Dr. Susanne Soretz C dC > X dX (48) Wettbewerb SS 2016 108 / 190 Ursachen für Skalenvorteile Technische Ursachen: Das Volumen steigt schneller als die Oberfläche. Dadurch kann beispielsweise die beförderte Wassermenge verdoppelt werden, während die Kosten für Rohre nur weniger stark steigen. Spezialisierte Produktionsfaktoren: Bei einer Ausweitung der Produktionsmenge können spezialisierte Produktionsfaktoren besser ausgelastet werden. Es ist dann lohnend, spezialisierte Arbeitskräfte einzustellen oder Spezialmaschinen anzuschaffen. Transaktionskosten: In der Regel steigen die Transaktionskosten unterproportional: Beschaffung größerer Mengen je Transaktion; häufigere Transaktionen Gesetz der großen Zahl: Störungen im Produktionsprozess werden besser kalkulierbar, so dass beispielsweise Ersatzlager oder Überkapazitäten geringer ausfallen können. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 109 / 190 Die Kosten bei Subadditivität X X bei Produktionsmengen bis zum Minimum der DK herrschen Skalenvorteile, danach überwiegen die steigenden Kosten (Überstunden, etc.) bei erheblichen Skalenvorteilen wird das Minimum der DK erst bei einer großen Produktionsmenge erreicht falls die Skalenvorteile immer wirken, haben die DK kein Minimum Prof. Dr. Susanne Soretz Wettbewerb SS 2016 110 / 190 Marktverhalten im natürlichen Monopol Mengenanpassendes Verhalten ist unmöglich: max G =PX − C(X ) X ➩ ∂G = ∂X ➩ P = GK (49) (50) P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 111 / 190 ➜ die Erlöse sind kleiner als die Kosten ➜ es entstehen Verluste ➜ bei sinkenden DK führt mengenanpassendes Verhalten immer zu Verlusten ➜ der größte Produzent kann alle anderen Produzenten unterbieten und vom Markt verdrängen dann ist der Weg frei für monopolistische Preissetzung Prof. Dr. Susanne Soretz Wettbewerb SS 2016 112 / 190 Monopolistische Preissetzung im natürlichen Monopol: P X die Höhe des Gewinns richtet sich nach der Differenz zwischen Preis im Cournot’schen Punkt und Durchschnittskosten bei dieser Produktionsmenge denkbar ist auch der Fall, dass der Monopolist im Cournot’schen Punkt Nullgewinne oder gar Verluste macht Prof. Dr. Susanne Soretz Wettbewerb SS 2016 113 / 190 Therapien des natürlichen Monopols Dilemma: einerseits ist die Produktion in nur einem Unternehmen mit geringeren Kosten verbunden: Effizienzvorteil der Größe andererseits führt Monopolmacht zu ineffizienter Allokation: GRS 6= GRT Drei mögliche Lösungen: (Milton Friedman: „Drei Übel“) 1. Lösung: das Monopol zum Staatsbetrieb machen (Bsp.: frühere Post oder Bahn, Müllabfuhr) Vorteil: Es kann (theoretisch) Pareto-effiziente Produktionsmenge „befohlen“ werden Nachteil: Tendenz zur Bürokratisierung, sog. X-Ineffizienz; deshalb heute selten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 114 / 190 2. Lösung: das Monopol in privater Hand belassen und staatlich regulieren (Bsp.: Gasversorgung) heute am häufigsten gewähltes „geringstes“ Übel, z.B. Eingriff in die Preisgestaltung ➜ detaillierte Besprechung im folgenden Kapitel 3. Lösung: Nichtstun, d. h. das Monopol unter vollständiger privater Verfügungsmacht belassen ➜ insbesondere, wenn man mit Nachfragewachstum rechnet, so dass die Kosten nicht mehr subadditiv sind der Markt bestreitbar ist, so dass potenzielle Konkurrenz den Monopolisten diszipliniert die Lösungen 1. und 2. noch schlechter sind Prof. Dr. Susanne Soretz Wettbewerb SS 2016 115 / 190 4 Regulierung Quelle: Borrmann/Finsinger (Kap. 6,7 und 10) Die wichtigsten Formen der Regulierung sind: Preissetzung durch den Staat: Grenzkostenpreisbildung würde zum sozialen Optimum führen, allerdings entstehen Verluste, die durch den Staat ausgeglichen werden müssen. Durchschnittskostenpreisbildung (auch: Ramsey-Preise, Eigenwirtschaftlichkeitsgebot, Gebot der Kostendeckung) vermeidet das Verlustproblem, allerdings bleiben das Effizienzund das Informationsproblem bestehen. Regulierung der Tarifgestaltung: Der zweigliedrige Tarif ermöglicht, die bei Grenzkostenpreisen entstehenden Verluste über Grundgebühren zu decken. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 116 / 190 Eingriff in die Preisgestaltung durch Subventionen: Durch Subventionen kann der Grenzerlös des Monopolisten so weit erhöht werden, dass sein Gewinnmaximum gerade bei der sozial optimalen Produktionsmenge liegt. Ausschreibung des Monopols: Wer bereit ist zum geringsten Preis anzubieten, darf Monopolist sein. Ersetzt Wettbewerb im Markt durch Wettbewerb um den Markt. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 117 / 190 4.1 Grenzkostenpreisbildung Grenzkostenpreisbildung führt (theoretisch) zur Realisierung des sozialen Optimums: P X Mengenausweitung ist so lange wohlfahrtssteigernd, wie der Grenznutzen (sh. Nachfrage) über den Grenzkosten liegt Prof. Dr. Susanne Soretz Wettbewerb SS 2016 118 / 190 In der Praxis entstehen jedoch Probleme: Effizienzproblem: ➩ keine Notwendigkeit zur Kostenminimierung ➩ ineffiziente Produktion ➩ kein Anreiz zur Umsetzung technischen Fortschritts Informationsproblem: ➩ Grenzkostenfunktion muss bekannt sein, auch Veränderungen der Grenzkosten bei Kapazitätsveränderungen ➩ wenig verlässliche Informationen aus dem Unternehmen ➩ Grenzkosten werden zu hoch und Nachfrage zu gering ausgeben Prof. Dr. Susanne Soretz Wettbewerb SS 2016 119 / 190 Anpassung an veränderte Bedingungen: ➩ Anpassung administrativ festgelegter Preise nicht hinreichend flexibel ➩ Anpassungen u. U. auch politisch schwer durchsetzbar Mittelaufbringung: ➩ Wohlfahrtsverluste (bspw. aus Steuern auf anderen Märkten) zusätzlich zu der zu erhebenden Summe ➩ Subvention zum Verlustausgleich an einen Monopolisten erzeugt u. U. politischen Widerstand Prof. Dr. Susanne Soretz Wettbewerb SS 2016 120 / 190 4.2 Ramsey-Preise Durchschnittskostenpreise maximieren die soziale Wohlfahrt unter der Nebenbedingung der Kostendeckung: P X ➜ es entsteht ein Wohlfahrtsverlust gegenüber Grenzkostenpreisen Prof. Dr. Susanne Soretz Wettbewerb SS 2016 121 / 190 Spezialfall: (teilweise) preisunelastische Nachfrage Beispiele: Telefon, Strom, Gasversorgung P X Preis kann ohne Wohlfahrtsverlust erhöht werden Verlustdeckung durch höhere Preise ist wohlfahrtsneutral aber höhere Preise entsprechen einer regressiven Besteuerung, somit aus Verteilungssicht problematisch Prof. Dr. Susanne Soretz Wettbewerb SS 2016 122 / 190 Bewertung der Durchschnittskostenpreise: Effizienzproblem so wie bei Grenzkostenpreisen: ➩ kein Anreiz zu effizientem Faktoreinsatz ➩ kein Anreiz zur Umsetzung von kostensparendem technischen Fortschritt Informationsproblem so wie bei Grenzkostenpreisen: ➩ zu regulierendes Unternehmen ist im Besitz der Informationen und hat keinen Anreiz, diese preiszugeben Anpassung an veränderte Rahmenbedingungen: unverändert problematisch Durchschnittskostenpreise verhindern Verluste und das damit verbundene Mittelaufbringungsproblem Prof. Dr. Susanne Soretz Wettbewerb SS 2016 123 / 190 Ramsey-Preise im Mehrproduktfall: Durchschnittskostenpreis lässt sich nicht mehr sinnvoll definieren viele Preiskombinationen denkbar, die die Nullgewinnbedingung erfüllen welche Preise sollten für ein Wohlfahrtsmaximum gesetzt werden? Gesucht ist der maximale soziale Überschuss bei Kostendeckung (sog. Ramsey-Problem) max P 1 ,P 2 KR + PR Prof. Dr. Susanne Soretz u. N. G = 0 Wettbewerb SS 2016 (51) 124 / 190 max P 1 ,P 2 KR 1 + KR 2 + P 1 · X 1 (P 1 ) + P 2 · X 2 (P 2 ) − C(X 1 , X 2 ) u. N. P 1 · X 1 (P 1 ) + P 2 · X 2 (P 2 ) − C(X 1 , X 2 ) = 0 (52) ➩ L = (53) ➩ ∂L = ∂ P1 (54) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 125 / 190 ➩ (P 1 − CX 1 )/P 1 η 2 = (P 2 − CX 2 )/P 2 η 1 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 (55) 126 / 190 Ergebnisse: Der (Gemeinkosten-)Aufschlag auf die GK sollte um so größer sein, je geringer die Preiselastizität der Nachfrage für das jeweilige Gut ist. Bei unelastischer Nachfrage wirkt ein Preisaufschlag so wie eine Kopfsteuer: verzerrungsfreie Möglichkeit der Verlustabdeckung. Je nach der Höhe der Preiselastizitäten kann es sozial optimal sein, Güter mit elastischer Nachfrage nahe an den Grenzkosten anzubieten und die Fixkosten durch um so höhere Preisaufschläge auf Güter mit weniger elastischer Nachfrage zu decken ➩ interne Subventionierung Beispiel: Im Fernverkehr der Bahn werden höhere Preise berechnet, um im Nahverkehr die Preise reduzieren zu können. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 127 / 190 noch Ergebnisse: Ramsey-Preise stehen im Widerspruch zu verbreiteten Gerechtigkeitsvorstellungen: besonders hohe Preisaufschläge sollen den Nachfragern auf Märkten „aufgebürdet“ werden, wo es schlecht möglich ist auszuweichen. Oft sind davon insbesondere geringer verdienende Nachfrager betroffen (Reiche können auf den Privatjet ausweichen, Arme müssen die Preiserhöhung im öffentlichen Nahverkehr hinnehmen) Bei Neueinführung von Ramsey-Preisen sind die Lasten ungleich verteilt, das reduziert u. U. die politische Durchsetzbarkeit. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 128 / 190 4.3 Tarifgestaltung Wenn es möglich ist, verschiedene Preise in Abhängigkeit vom Verbrauch zu setzen, dann können Verluste trotz Grenzkostenpreisen vermieden werden. Das geht nur, wenn Güter nicht weiterverkauft werden können, sonst gäbe es Zwischenhändler, die zu den jeweils günstigsten Bedingungen einkaufen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 129 / 190 Varianten: Zweigliedrige Tarife, d. h. Grundgebühr + Stückpreis, mit dem Spezialfall des Pauschaltarifs Blocktarife, d. h. verschiedene Stückpreise in verschiedenen Mengenintervallen optionale Tarife, d. h. verschiedene Kombinationen von Grundgebühren und Stückpreisen nach Wahl des Konsumenten Beispiele: Vesorgungsbetriebe (Strom, Gas, Wasser, Telefon), Bahncard (optional), Jahreskarten für Zoo/Schwimmbad o. ä. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 130 / 190 Zweigliedriger Tarif: Grundgebühr L fällt für den Zugang zum Konsum an Stückpreis P fällt für die Nutzung einer Einheit an Idee: die konsumierte Menge richtet sich nach dem Stückpreis der entstehende Verlust kann durch die Grundgebühr gedeckt werden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 131 / 190 Funktionsweise des zweigliedrigen Tarifs: Wie viel des Gutes wird der Konsument nachfragen? ➩ Ausweitung der Nachfrage lohnt sich, so lange der Grenznutzen größer ist als der Stückpreis (unveränderte Argumentation) Wird das Gut überhaupt nachgefragt? ➩ Das Gut wird nachgefragt, wenn der Gesamtnutzen positiv ist, d. h. nach Zahlung der Grundgebühr positiver Nutzen verbleibt. P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 132 / 190 Ergebnisse: So lange der Nutzen groß genug ist (der Stückpreis gering genug), verändert sich die Nachfrage durch die Grundgebühr nicht. bei Grenzkostenpreisen wird somit die optimale Menge realisiert durch die Grundgebühr entstehen keine Verluste Prof. Dr. Susanne Soretz Wettbewerb SS 2016 133 / 190 der gewinnmaximierende zweigliedrige Tarif: P X Stückpreis im Cournot’schen Punkt maximiert den Gewinn Grundgebühr erlaubt darüber hinaus Abschöpfung der Konsumentenrente und weitere Erhöhung des Gewinns Prof. Dr. Susanne Soretz Wettbewerb SS 2016 134 / 190 Bewertung des zweigliedrigen Tarifs: Effizienzproblem bleibt erhalten: wenn der Nutzen der Haushalte hinreichend groß ist, können Gebühren auch über das notwendige Maß erhöht werden ➩ auch größere Verluste können gedeckt werden Informationsproblem: bleibt erhalten, da Stückpreis und Grundgebühr staatlich festgelegt werden müssen Problem der Anpassung an veränderte Rahmenbedingungen bleibt erhalten Mittelaufbringung: erfolgt durch die Nutzer des Gutes, dadurch keine zusätzlichen Verzerrungen auf anderen Märkten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 135 / 190 4.4 Subvention Durch Zahlung einer Subvention können monopolistische Gewinnmaximierung und soziales Optimum in Übereinstimmung gebracht werden: P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 136 / 190 Ergebnisse: (Stück-)Subvention erhöht den Grenzerlös, ergo weitet der Monopolist seine Produktionsmenge aus bei optimaler Subvention liegt der Cournot’scher Punkt im sozialen Optimum der sozialer Überschuss ist dann maximal Prof. Dr. Susanne Soretz Wettbewerb SS 2016 137 / 190 Bewertung der Regulierung durch Subvention: Effizienzproblem: ist gelöst durch Gewinnmaximierung des Monopolisten Informationsproblem: wesentlich geringer, da kein direktes Interesse des Unternehmens an Falschinformation besteht Anpassung an veränderte Rahmenbedingungen: Subventionssatz muss neu bestimmt und festgelegt werden, aber auch hier Vereinfachung, da das Unternehmen keinen Anreiz zu Falschinformation mehr hat Mittelaufbringung: Subventionszahlung ist noch höher als der bei GK-preisen nötige Verlustausgleich ➩ Verzerrung durch Mittelaufbringung ist groß ➩ massiver Eingriff in die Verteilung: Monopole nutzen ihre Marktmacht zur Gewinnerzielung und bekommen darüber hinaus Subvention ➩ politische Probleme bei der Umsetzung: geringe Akzeptanz einer Subvention an einen gewinnmaximierenden Monopolisten Prof. Dr. Susanne Soretz Wettbewerb SS 2016 138 / 190 4.5 Ausschreibung eines natürlichen Monopols Idee: Wettbewerb im Markt wird durch Wettbewerb um den Markt ersetzt. Bestreitbare Märkte hätten den gleichen Effekt: Ein Monopolist, der fürchten muss, durch seinen Monopolgewinn Konkurrenten in den Markt zu locken, wird zu Durchschnittspreisen (➩ Nullgewinn) anbieten. Die meisten natürlichen Monopole sind aber durch hohe Markteinoder -austrittskosten gekennzeichnet, somit nicht bestreitbar. Der fehlende Wettbewerbsdruck kann dann durch regelmäßig wiederkehrende Ausschreibungen des Monopols ersetzt werden. Beispiele: Ausschreibung der Müllabfuhr, Ausschreibung von Nahverkehrslinien Prof. Dr. Susanne Soretz Wettbewerb SS 2016 139 / 190 Funktionsweise der Ausschreibung: Konzession/Lizenz, einen Markt zu bedienen, wird ausgeschrieben Gebote um die Lizenz sind die Güterpreise Zuschlag geht an das Unternehmen, das den geringsten Preis geboten hat P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 140 / 190 Bewertung des Ausschreibungsverfahrens: Effizienzproblem: gelöst durch die Nutzung der Wettbewerbskräfte (ineffizient produzierende Unternehmen werden unterboten) Informationsproblem: gelöst, da Informationen über Kostenverläufe und Nachfrage nur innerhalb des Unternehmens benötigt werden jedoch: Auswahl der geeigneten Qualität durch den Staat (andernfalls Qualitätsminimierung durch Monopolisten) Beurteilung von Angeboten bei mehrteiligen Tarifen oder im Mehrproduktfall erfordert detaillierte Kenntnisse der Nachfragefunktion, z. T. auch der Kostenverläufe Kollusion zwischen den Bietern muss ausgeschlossen werden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 141 / 190 Anpassung an veränderte Rahmenbedingungen: immer dann problematisch, wenn während des Lizenzzeitraums Anpassungen nötig werden Mittelaufbringung: gelöst durch Durchschnittskostenpreise versunkene Kosten können entweder durch geeignete Wahl des Lizenzzeitraums unbedeutend werden (Bsp. Lizenzzeitraum = Lebensdauer eines Müllwagens) oder durch staatliche Bereitstellung der irreversiblen Investitionen aus dem Markt genommen werden (Bsp. Schienennetz versus Betreibung der Bahnlinie) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 142 / 190 5 Das Monopson und das bilaterale Monopol Quelle: Wied-Nebbeling Kap. II.3 und II.4; Wiese Kap. O.4 Monopson: Ein Nachfrager trifft auf viele Anbieter Der Nachfrager übt Marktmacht aus und wählt den für ihn besten Punkt auf der Angebotsfunktion. Beispiele: Lebensmittelketten als Nachfrager von Agrarprodukten, VW als Nachfrager von spezifischen Zwischenprodukten bilaterales Monopol: Ein Nachfrager trifft auf einen Anbieter Sowohl Nachfrager als auch Anbieter verfügen über Marktmacht. Das Marktergebnis hängt davon ab, wessen Macht größer ist, das kann von der Existenz substitutiver Güter abhängen, aber auch situationsabhängig sein. Beispiel: Arbeitsmarkt, Rüstungsgüter. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 143 / 190 5.1 Das Monopson Nachfrage des Monopsonisten: Für einen Monopsonisten ist der Güterpreis nicht mehr exogen. Der Zusammenhang zwischen Güterpreis und Güterangebot ist durch die Angebotsfunktion beschrieben. Wenn der Monopsonist mehr nachfragt, steigt der Preis, den er für das Gut bezahlen muss. Der Monopsonist wählt den für ihn optimalen Punkt auf der Angebotsfunktion. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 144 / 190 Marktmacht im Monopson: Partialanalyse P X Erhöht der Monopsonist seine Nachfrage, dann steigt sein Nutzen um den Grenznutzen steigen seine Ausgaben um die Grenzausgabe ∂ P(X )X ∂ P(X ) = X + P(X ) > P ∂X X } | ∂{z (56) >0 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 145 / 190 Der Monopsonist wird seine Nachfrage ausweiten, bis der Grenznutzen mit der Grenzausgabe übereinstimmt: GN = ➩ ∂ P(X ) X + P(X ) ∂X 1 GN − P = P ηA Monopsongrad (57) der Monopsonist nutzt seine Marktmacht, um den Preis unter den Grenznutzen zu senken der Monopsonist reduziert die Nachfrage (im Vergleich zum Mengenanpasser), weil dadurch der Preis sinkt dadurch kann er seinen Nutzen insgesamt steigern Prof. Dr. Susanne Soretz Wettbewerb SS 2016 146 / 190 Der Monopsongrad 1/ηA : der Monopsongrad ist positiv und liegt zwischen null und unendlich die prozentuale Abweichung des Preises vom Grenznutzen ist um so größer, je unelastischer das Güterangebot ist, d. h. je größer der Monopsongrad ist geringe Elastizität des Güterangebots bedeutet, dass ein Preisabschlag leicht durchgesetzt werden kann, ohne dafür die nachgefragte Menge stark senken zu müssen, der Monopsonist hat also große Marktmacht wenn es nahe Substitute gibt (andere Güter, die die Anbieter stattdessen produzieren können), dann liegt der Monopsongrad nahe null, die Marktmacht des Monopsonisten ist gering Prof. Dr. Susanne Soretz Wettbewerb SS 2016 147 / 190 P X durch den Preisabschlag sinkt die angebotene Menge ➜ es entsteht ein Wohlfahrtsverlust Prof. Dr. Susanne Soretz Wettbewerb SS 2016 148 / 190 Ergebnisse Monopson: der Monopsonist nutzt seine Marktmacht, um das Marktergebnis zu seinen Gunsten zu verbessern er reduziert seine Nachfrage, um den Preis (unter den Grenznutzen) zu senken die Marktmacht ist um so größer, je geringer die Preiselastizität der Angebots ist es entsteht ein Wohlfahrtsverlust, da die nachgefragte Menge sinkt alle Ergebnisse des Monopols sind übertragbar in der Regel dürfte ein Monopson keine stabile Marktform sein staatliche Regulierung kann erforderlich sein Prof. Dr. Susanne Soretz Wettbewerb SS 2016 149 / 190 Marktmacht im Monopson: allgemeines Gleichgewicht Monopson in Sektor 1: Gewinnmaximierung mengenanpassender Unternehmen ➩ GRTS 1 = w /r = GRTS 2 ➩ effiziente Produktion ➩ GRT = p 1 /p 2 Nutzenmaximierung des Nachfragers: max U(X 1 , X 2 ) u. N. y = p 1 (X 1 )X 1 + p 2 X 2 X 1 ,X 2 L = ∂L = ∂X1 ∂L = ∂X2 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 150 / 190 ➩ ➩ p 1 1 + η11 p1 UX 1 A = > UX 2 p2 p2 GRS > GRT ➩ ineffiziente Koordination X2 (58) X2 X1 X1 Die Wohlfahrt würde steigen, wenn mehr von Gut 1 und dafür weniger von Gut 2 produziert würde. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 151 / 190 Realistischer: Monopsonist auf dem Arbeitsmarkt Für einen Monopsonisten auf dem Arbeitsmarkt ist der Lohnsatz nicht mehr exogen. Der Zusammenhang zwischen Lohnsatz und Arbeitsangebot ist durch die Arbeitsangebotsfunktion beschrieben. max G(K , L) = PX (K , L) − w (L)L − rK K ,L ∂G = ∂K ∂G = ∂L (59) (60) (61) ➜ Grenzausgabe w (1 + ηw ,L) > w ➜ der Lohn für alle Beschäftigten muss erhöht werden Prof. Dr. Susanne Soretz Wettbewerb SS 2016 152 / 190 Monopsongrad: PXL − w 1 = w ηL,w (62) Der Monopsongrad ist positiv und liegt zwischen null und unendlich. Die prozentuale Abweichung des Lohnsatzes vom Wertgrenzprodukt der Arbeit ist um so größer, je unelastischer das Arbeitsangebot ist. Geringe Elastizität des Arbeitsangebots bedeutet, dass die Arbeiter schlecht ausweichen können (stark spezialisierte Arbeiter, regional einziger Arbeitgeber) Wenn es gute Substitute gibt (andere Arbeitgeber), dann liegt der Monopsongrad nahe null. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 153 / 190 w L Ein Monopsonist nutzt seine Marktmacht, um zu einem geringeren Lohn weniger Arbeit nachzufragen. Die produzierte Menge ist dadurch suboptimal gering. Es entsteht ein Wohlfahrtsverlust (Dreieck). Zusätzlich erfolgt eine Umverteilung zu Gunsten des Monopsonisten. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 154 / 190 5.2 Das bilaterale Monopol Bilaterales Monopol auf dem Gütermarkt: Ein Monopsonist würde gemäß „Grenznutzen = Grenzausgabe“ entscheiden und dadurch eine geringere Güternachfrage bei geringerem Preis realisieren (s.o.). Ein Monopolist würde gemäß „Grenzerlös = Grenzkosten“ entscheiden. P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 155 / 190 Der Preis, den der Monopsonist zahlen würde, ist geringer als P ∗ . Der Preis, den der Monopolist setzen würde, ist größer als P ∗ . Der Preis als Verhandlungsergebnis im bilateralen Monopol hängt von der Verhandlungsmacht der beiden Seiten ab: Alternative Produktion, alternative Konsumgüter,... Der Preis im bilateralen Monopol kann größer oder kleiner als P ∗ sein. Die Menge wird auf jeden Fall geringer sein als X ∗ ! Prof. Dr. Susanne Soretz Wettbewerb SS 2016 156 / 190 Beispiel Arbeitsmarkt: Der Monopsonist ist einziger Arbeitsnachfrager am Ort, würde gemäß „Wertgrenzprodukt = Grenzausgabe“ entscheiden und dadurch eine geringere Arbeitsnachfrage bei geringerem Lohnsatz realisieren (s.o.). Der Monopolist ist einziger Anbieter von Arbeit oder Angebotskartell (d. h. Gewerkschaft) und würde gemäß „Grenzerlös = Grenzkosten“ entscheiden, Grenzkosten signalisieren das Arbeitsleid, entsprechen der Arbeitsangebotskurve, Grenzausgabe resultiert aus der Arbeitsangebotskurve Wertgrenzprodukt entspricht der Arbeitsnachfragekurve, Grenzerlös resultiert aus der Arbeitsnachfrage Prof. Dr. Susanne Soretz Wettbewerb SS 2016 157 / 190 w L Der Monopsonist würde wM.pson < w ∗ setzen, die Gewerkschaft als Monopolist würde wM.pol > w ∗ setzen. Der Lohn als Verhandlungsergebnis im bilateralen Monopol hängt von der Verhandlungsmacht der beiden Seiten ab: Glaubwürdigkeit von Streiks/Aussperrungen, Höhe der Arbeitslosigkeit, politische Einflussnahme, etc. Im bilateralen Monopol kann der Lohn größer oder kleiner als w ∗ sein, auf jeden Fall ist Lbil < L∗ . Prof. Dr. Susanne Soretz Wettbewerb SS 2016 158 / 190 Ergebnisse bilaterales Monopol: das Verhandlungsergebnis im bilateralen Monopol hängt von der Macht der beiden Marktseiten ab über die Höhe des resultierenden Preises sind ohne weitergehende Annahmen keine Aussagen möglich die gehandelte Menge wird eindeutig suboptimal gering sein es entsteht ein Wohlfahrtsverlust auch das bilaterale Monopol ist inhärent instabil, da die Extragewinne neue Marktteilnehmer anziehen sollte die Marktmacht länger bestehen bleiben, ist staatliche Regulierung nötig Prof. Dr. Susanne Soretz Wettbewerb SS 2016 159 / 190 6 Das Oligopol Quelle: Borrmann/Finsinger (Kap. 3) und Wied-Nebbeling (Kap. IV.1-IV.3 und VI.2) Oligopol: wenige Anbieter stehen vielen Nachfragern gegenüber ➩ jeder Anbieter hat Marktmacht, das Marktergebnis hängt aber auch vom Verhalten der anderen Anbieter ab Prof. Dr. Susanne Soretz Wettbewerb SS 2016 160 / 190 Erinnerung: Wie viele Anbieter auf einem Markt tätig sind, hängt von der Kostenstruktur ab: X X wenn die Kostenstruktur im relevanten Bereich der Nachfrage subadditiv ist, kann langfristig nur ein Anbieter auf dem Markt bestehen wenn die Größenvorteile bei sehr kleinen Mengen schon verschwinden, ist Platz für sehr viele Anbieter ➜ vollkommene Konkurrenz (Bsp. Friseure, Bäcker) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 161 / 190 Oligopol: X „wenige“ Anbieter sind auf dem Markt tätig, wenn Subadditivität zwar nicht bis in den relevanten Bereich der Nachfrage reicht, aber den Marktzutritt neuer Anbieter behindert ➜ jeder Anbieter spürt die Auswirkungen des Verhaltens der anderen Anbieter Prof. Dr. Susanne Soretz Wettbewerb SS 2016 162 / 190 Marktverhalten: Jeder Anbieter muss Vorstellungen über das Verhalten der anderen Anbieter entwickeln. (Beispiel: Marktführer und Marktfolger) Jeder Anbieter kann Mengen- oder Preisstrategie verfolgen. Realistisch: Zunächst Mengenfestlegung (Kapazitätsentscheidung), dann Preisfestlegung. Wegen der Möglichkeit zu strategischem Verhalten sind viele Verhaltensweisen im Oligopol möglich Beispiele: Mengenwettbewerb mit verschiedenen Machtverteilungen Preiswettbewerb Kollusion Das konkrete Ergebnis hängt von den jeweiligen Randbedingungen und den beteiligten Entscheidungsträgern (!) ab. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 163 / 190 6.1 Mengenwettbewerb nach Cournot Die Anbieter stehen der gemeinsamen Marktnachfrage gegenüber: Gi = P(X )Xi − Ci (Xi ) wobei X = X1 + . . . + Xn (63) Gegeben das Verhalten (Ausbringungsmenge) der anderen Anbieter, kann man das optimale Verhalten des Anbieters i bestimmen: maxGi = P(X )Xi − Ci (Xi ) Xi ➩ (64) ∂ Gi = ∂ Xi Prof. Dr. Susanne Soretz Wettbewerb SS 2016 164 / 190 ➩ P − Ci ′ Xi 1 =− P X η (65) Die Oligopolisten nutzen ihre Marktmacht, um den Preis über die Grenzkosten anzuheben. Der relative Preisaufschlag ist um so größer, je größer der Marktanteil Xi /X ist. Bei Symmetrie (gleich große Oligopolisten) ist der Marktanteil um so größer, je weniger Anbieter auf dem Markt sind. Der relative Preisaufschlag ist um so größer, je unelatischer die Marktnachfrage reagiert, wie beim Monopol. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 165 / 190 Ergebnisse: Da der Preis höher ist als die Grenzkosten, entsteht ein Wohlfahrtsverlust. Es resultiert wettbewerbspolitischer Eingriffsbedarf wie beim natürlichen Monopol. Je weiter das Oligopol ist (mehr Oligopolisten), um so näher ist das Marktergebnis am sozialen Optimum. Je enger das Oligopol ist (weniger Oligopolisten), um so eher ist mit Verzerrungen zu rechnen, die der Regulierung bedürfen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 166 / 190 Beispiel: Oligopol mit linearer Nachfrage und gleichen, linearen Kosten lineare Nachfrage P = a − bX = a − b(X1 + . . . + Xn ) identische, lineare Kosten Ci ′ = c ∀i Für die Anbieter i bzw. j folgt: ∂ Gi = ∂ Xi ∂ Gj = ∂ Xj ➩ Xi = Xj (Symmetrie wg. identischer Kosten) (66) Spezialfall Duopol: X1 + X = ➩ a−c b X1 = ➩ a − c X2 − 2b 2 Prof. Dr. Susanne Soretz und analog X2 = Wettbewerb SS 2016 a − c X1 − 2b 2 167 / 190 X1 X2 Das Gleichgewicht liegt im Schnittpunkt der beiden Reaktionsfunktionen und ist stabil. Wegen Symmetrie X1 = X2 : ➩ 1 a−c ➩ 3 b Cournot’sche 2/3-Lösung ➩ X1 = X2 = Prof. Dr. Susanne Soretz X= Wettbewerb SS 2016 2 a−c 3 b (67) 168 / 190 Gleichgewicht bei n Oligopolisten: X = nXi ➩ ➩ X= n a−c n+1 b (68) P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 169 / 190 Erweiterung: Marktführerschaft nach Stackelberg Einer der Oligopolisten könnte die Reaktion des anderen antizipieren: n könnte die Reaktionsfunktionen der anderen kennen und berücksichtigen. Dann wählt n auf den Reaktionsfunktionen der anderen Oligopolisten denjenigen Punkt, der seinen Gewinn maximiert. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 170 / 190 Alle Marktfolger i = 1, . . . , n − 1 betrachten die Gesamtmenge als von ihrer eigenen Entscheidung unabhängig (wie oben): maxGi = P(X )Xi − Ci (Xi ) Xi ➩ mit P = a − bX und Ci′ = c (69) ∂ Gi = ∂ Xi ∂ Gj = ∂ Xj ➩ Xi = Xj (70) Marktfolger verhalten sich wie Cournot-Oligopolisten. Gesamtangebot X = (n − 1)Xi + Xn Prof. Dr. Susanne Soretz Wettbewerb SS 2016 171 / 190 Die Reaktionsfunktion der Marktfolger ist: −bXi + a − bX − c = 0 mit X = (n − 1)Xi + Xn ➩ a − c Xn − bn n ➩ Xi = ➩ ∂ Xi = ∂ Xn (71) (72) Der Marktführer maximiert seinen Gewinn maxGn = P(X )Xn − Cn (Xn ) Xn ➩ mit P = a − bX und Cn′ = c ∂ Gn = ∂ Xn und beachtet dabei die Reaktionsfunktionen der Marktfolger Prof. Dr. Susanne Soretz Wettbewerb SS 2016 172 / 190 ➩ Xn = ➩ Xi = ➩ X= a−c 2b Prof. Dr. Susanne Soretz Monopolmenge, unabhängig von n (73) (74) Wettbewerb SS 2016 173 / 190 Beispiel Duopol: n = 2 Marktführer 2 bietet Monopolmenge an: X2 = a−c 2b (75) Marktfolger 1 bietet halbe Monopolmenge an: X1 = a−c 4b (76) Ergebnisse: Der Marktführer hat einen größeren Marktanteil als im Cournot-Gleichgewicht. Der Marktfolger produziert eine geringere Menge. Die Gesamtmenge ist größer, der Wohlfahrtsverlust geringer. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 174 / 190 P X (Hier) ohne Erklärung: die Festlegung von Marktführer und Marktfolger ➜ Marktfolger könnte versuchen, zum Marktführer zu werden ➜ beide Duopolisten würden dann je (a − c)/2b anbieten, insgesamt würde die Konkurrenzmenge erzeugt ➜ beide Duopolisten würden sich aber verbessern, wenn sie ihr Angebot reduzierten Generell gilt: Je geringer das „Einvernehmen“ zwischen den Oligopolisten, um so größer ist die Gesamtmenge und um so geringer ist der Wohlfahrtsverlust. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 175 / 190 6.2 Preiswettbewerb nach Bertrand Setzen die Oligopolisten direkt die Preise, so ist das Gleichgewicht grundlegend anders: Es resultieren Grenzkostenpreise und somit das soziale Optimum. Argumentation: Wenn einer der Oligopolisten seinen Preis marginal senkt, so zieht er die gesamte Nachfrage auf sich. Die Umsatzeinbuße durch die Preissenkung wird durch den starken Zuwachs der abgesetzten Menge mehr als ausgeglichen, so dass der Gewinn steigt. Da den anderen Oligopolisten so der Verlust der gesamten Absatzmöglichkeit droht, senken sie ihrerseits den Preis. Dieser Prozess setzt sich fort, bis Grenzkostenpreise erreicht sind; eine weitere Preissenkung wäre gewinnmindernd. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 176 / 190 Würdigung: Die Ergebnisse des Preiswettbewerbs nach Bertrand sind nicht robust: Bei Kapazitätsgrenzen der einzelnen Anbieter oder steigenden Grenzkosten kann nicht mehr sicher von Grenzkostenpreisen ausgegangen werden. Auch Produktdifferenzierung würde Grenzkostenpreise verhindern, da ein Oligopolist dann nicht mehr durch marginale Preissenkungen die gesamte Nachfrage auf sich ziehen kann. Aus dem Bertrand-Gleichgewicht darf nicht der Optimismus abgeleitet werden, dass trotz Marktmacht im Oligopol sozial optimale Marktergebnisse resultieren. Das Bertrand-Modell belegt vor allem die Bedeutung der Annahmen über das Unternehmensverhalten und die strategische Interaktion im Oligopol. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 177 / 190 Nobelpreis 2014 an Jean Tirole Jean Tirole erhielt 2014 den Nobelpreis für Wirtschaftswissenschaften „for his analysis of market power and regulation“ Tirole hat viel über Oligopole gearbeitet er zeigt, dass man nicht einfache Prinzipien auf alle Oligopole anwenden kann (z.B. Preisobergrenzen), sondern die Wettbewerbspolitik immer die speziellen Bedingungen einer Industrie berücksichtigen muss seine Ideen haben Eingang in die Wettbewerbspolitik gefunden: heute sind viel stärker Ökonomen beteiligt, nicht nur Juristen Prof. Dr. Susanne Soretz Wettbewerb SS 2016 178 / 190 6.3 Wettbewerbsbeschränkung: Kooperation Quelle: Wied-Nebbeling (Kap. VI 2.2) Da sich die Gewinnmöglichkeiten der Oligopolisten durch Machtkämpfe verschlechtern, liegt es nahe, „gemeinsame Sache“ zu machen. Implizite (stillschweigende) Kooperation (geringster Kooperationsgrad) Einigung auf Wettbewerbsregeln (auch: Niedrigstpreisgarantien ➜ reduzierte ein Anbieter den Preis, so würden alle anderen den Preis übernehmen ➜ Preissenkungen erhöhen nicht den Gewinn ➜ Preise über den GK können aufrecht erhalten werden) Verhaltensabstimmung (Quotierung, Preisabsprachen) Kartellbildung Prof. Dr. Susanne Soretz Wettbewerb SS 2016 179 / 190 gemeinschaftliche Maximierung des Gesamtgewinns durch Kartellbildung/Kollusion: G = P(X )X − C1 (X1 ) − . . . − Cn (Xn ) ∂G ➩ = ∂ X1 ∂G ➩ = ∂ Xi mit X = X1 + . . . + Xn die Gesamtproduktionsmenge wird so auf die Unternehmen verteilt, dass die Grenzkosten gleich hoch sind der (gemeinsame) Grenzerlös muss gleich den (einheitlichen) Grenzkosten sein Prof. Dr. Susanne Soretz Wettbewerb SS 2016 180 / 190 lineare Nachfrage P(X ) = a − bX und konstante Kosten c ∂P X + P = Ci′ ∂X a−c ➩ X= 2b ➩ (77) Die Gesamtmenge entspricht dann der Monopolmenge. Die Summe des Gewinns ist so maximal, ebenso der Wohlfahrtsverlust. P X Prof. Dr. Susanne Soretz Wettbewerb SS 2016 181 / 190 Die Mengenverteilung auf die Unternehmen hängt von den Kostenverläufen ab: Bei gleichen und konstanten Grenzkosten ist die Aufteilung irrelevant ➜ Aufteilung nach Marktanteilen vor Kartellbeginn oder gleichmäßig Bei steigenden und in allen Unternehmen identischen Grenzkosten erfordert Gewinnmaximierung einheitliche Produktionsmengen, was schwer durchsetzbar ist, wenn Unternehmen vor Kartellbeginn verschiedene Größen hatten. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 182 / 190 Bei steigenden und unterschiedlichen GK muss das Unternehmen mit den höchsten GK die geringste Menge produzieren ➜ Durchsetzung problematisch: P P Xi Prof. Dr. Susanne Soretz Wettbewerb SS 2016 X 183 / 190 Würdigung: Gewinnaufteilung ist problematisch, insbesondere bei unterschiedlichen Produktionsmengen müssen Ausgleichszahlungen ausgehandelt werden. Kartelle sind (wegen des Wohlfahrtsverlustes) verboten ➜ Zusammenschluss zu einem Unternehmen nicht möglich ➜ (illegale) Absprachen über das Marktverhalten: Mengenkontingente, Mindestpreise. So lange der einzelne Oligopolist damit rechnen kann, dass die anderen Kartellmitglieder sich an die Absprache halten, kann er unter Umständen seinen Gewinn durch eine Mengenausweitung erhöhen (siehe unten). Wegen der schlechten Sanktionsmöglichkeiten illegaler Absprachen sind Kartelle inhärent instabil (siehe OPEC), insbesondere bei vielen Oligopolisten. Je nach dem tatsächlichen Verhalten der Kartellteilnehmer können sie aber auch über lange Zeit gut funktionieren (sh. Mineralölkonzerne, Zucker) Prof. Dr. Susanne Soretz Wettbewerb SS 2016 184 / 190 Kartellstabilität: Ein Kartell ist dann instabil, wenn es eine vorteilhafte Außenseiterposition gibt. Erhöht ein Anbieter seine Produktionsmenge, dann steigt sein Gewinn, da die Kartellabsprache P > GK impliziert sinkt sein Gewinn, da der Preis bei hinreichendem Einfluss des Anbieters sinkt Eine vorteilhafte Außenseiterposition gibt es, wenn der Preis nicht zu stark fällt, so dass der Gewinnanstieg dominiert. Dann ist es für alle Kartellmitglieder lohnend, die Menge auszudehnen ➜ das Kartell bricht zusammen. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 185 / 190 der Außenseiter ist der Einzige, der seine Produktionsmenge erhöht: P P Xi X der erzielbare Preis sinkt weniger schnell, wenn nur der Außenseiter seine Menge erhöht, nicht alle Kartellmitglieder wenn jedoch alle Kartellmitglieder die Außenseiterposition einnehmen, bricht das Kartell zusammen Prof. Dr. Susanne Soretz Wettbewerb SS 2016 186 / 190 Wann gibt es eine vorteilhafte Außenseiterposition? Beispiel: lineare Nachfragefunktion P = a − bX , konstante Grenzkosten c ➩ Kartellmenge X K = a−c 2b XiK = a−c 2bn (78) Der Preis beträgt dann P= = a+c 2 (79) und der Gewinn eines Kartellmitglieds ist GiK = a+c a−c a−c −c 2 2bn 2bn Prof. Dr. Susanne Soretz Wettbewerb SS 2016 187 / 190 Der Außenseiter bestimmt seine gewinnmaximierende Produktionsmenge bei gegebenem Verhalten der Kartellmitglieder: P =a − b(X K + XA) = a+c = − bXA 2 (80) Der maximale Gewinn des Außenseiters ergibt sich aus a+c GA = − bXA XA − cXA = 2 ∂ GA = ∂ XA a−c ➩ XA = 4b a + 3c ➩ PA = = 4 Prof. Dr. Susanne Soretz Wettbewerb SS 2016 188 / 190 ➩ GA = a−c a + 3c a − c −c 4 4b 4b = Die Außenseiterposition ist vorteilhaft, wenn der Gewinn höher ist als im Kartell: GA ≷ GiK ➩ ➩ n≷4 Prof. Dr. Susanne Soretz (81) Wettbewerb SS 2016 189 / 190 Ergebnisse: Die Gewinnsteigerung durch Kooperation ist nur durchsetzbar, wenn alle Kartellmitglieder die Menge reduzieren. Aus dem Kartell auszubrechen (wenn alle anderen sich an die Mengenbeschränkung halten) ist lukrativ, wenn der Preis nicht zu stark sinkt. Der Preisrückgang wird um so größer ausfallen, je enger das Oligopol ist. Bei konstanten Grenzkosten und linearer Nachfragefunktion ist das Kartell instabil, sobald n > 4. Dann ist der Einfluss des einzelnen Anbieters auf den Preis so gering, dass die gewinnsteigerne Wirkung der Mengenausdehnung überwiegt. Prof. Dr. Susanne Soretz Wettbewerb SS 2016 190 / 190