A = c - Mathematik macht Freu(n)de

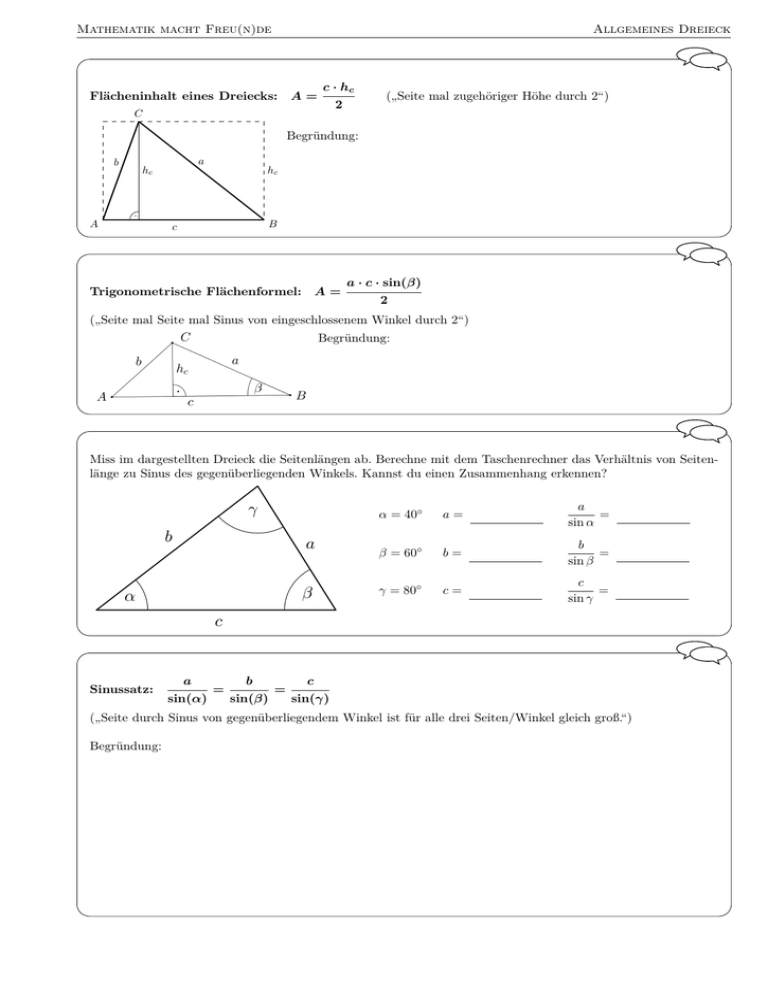
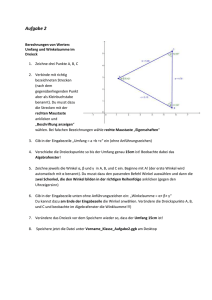
Mathematik macht Freu(n)de
Allgemeines Dreieck
Flächeninhalt eines Dreiecks:
A=
c · hc
2
C
(„Seite mal zugehöriger Höhe durch 2“)
Begründung:
b
A
a
hc
·
hc
B
c
A=
Trigonometrische Flächenformel:
a · c · sin(β)
2
(„Seite mal Seite mal Sinus von eingeschlossenem Winkel durch 2“)
Begründung:
Miss im dargestellten Dreieck die Seitenlängen ab. Berechne mit dem Taschenrechner das Verhältnis von Seitenlänge zu Sinus des gegenüberliegenden Winkels. Kannst du einen Zusammenhang erkennen?
Sinussatz:
a
sin(α)
=
b
sin(β)
=
α = 40◦
a=
a
=
sin α
β = 60◦
b=
b
=
sin β
γ = 80◦
c=
c
=
sin γ
c
sin(γ)
(„Seite durch Sinus von gegenüberliegendem Winkel ist für alle drei Seiten/Winkel gleich groß.“)
Begründung:
Mathematik macht Freu(n)de
Allgemeines Dreieck
c2 = a2 + b2 − 2 · a · b · cos(γ)
Cosinussatz:
γ
Spezialfall: γ = 90◦
(„Pythagoras mit Korrekturterm −2 · a · b · cos(γ)“)
b
a
=⇒ cos(γ) =
=⇒ c2 =
c
Begründung:
γ
x
b
·
h
a−x
c
Kochrezept:
Berechnung aller Seiten und Winkel eines allgemeinen Dreiecks
a) Eine Seitenlänge und zwei Winkel bekannt:
-) Dritter Winkel mit Winkelsumme 180◦
-) Seitenlängen mit Sinussatz
b) Zwei Seitenlängen und Winkel, der der längeren Seite gegenüberliegt, bekannt:
-) Spitzer Winkel mit Sinussatz
-) Dritter Winkel mit Winkelsumme 180◦
b
a
α
-) Dritte Seitenlänge mit Sinussatz
c) Zwei Seitenlängen und Winkel, der der kürzeren Seite gegenüberliegt, bekannt:
b
α
1) Sinussatz ; DOMAIN Error =⇒ keine Lösung
2) Sinussatz ; β = 90◦ =⇒ eine Lösung
3) Sinussatz ; spitzer Winkel β =⇒ zwei Lösungen (β2 = 180◦ − β)
d) Zwei Seitenlängen und der eingeschlossene Winkel bekannt:
-) Dritte Seitenlänge mit Cosinussatz
-) Spitzer Winkel mit Sinussatz
-) Dritter Winkel mit Winkelsumme 180◦
e) Drei Seitenlängen bekannt:
-) Größter Winkel mit Cosinussatz
-) Spitzer Winkel mit Sinussatz
-) Dritter Winkel mit Winkelsumme 180◦
Dieses Werk von Mathematik macht Freu(n)de unterliegt einer CC BY-NC-ND 4.0 Lizenz.
http://mathematikmachtfreunde.univie.ac.at