TU München Reinhard Scholz Physik Department, T33 Thomas

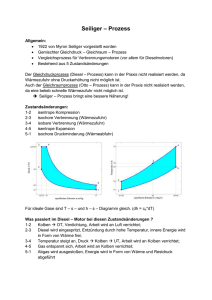
TU München
Reinhard Scholz
Physik Department, T33
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
http://www.wsi.tum.de/T33/Teaching/teaching.htm
Übung in Theoretischer Physik 5B (Thermodynamik)
Blatt 4
(Abgabe Di 20. Mai 2008 in Vorlesung)
1. Umwandlung von Arbeit in innere Energie [3 Punkte]
In einem wärmeisolierten, kreisförmigen Zylinder, der mit Stickstoff gefüllt ist, bewegt sich ein Kolben mit
Durchmesser d = 20 cm um 12.5 cm nach oben, während dem Gas über einen Ventilator Arbeit zugeführt
wird. Zusätzlich zur Gewichtskraft des Kolbens mit einer Masse von m = 80 kg wirkt von außen auf den
Kolben ein Luftdruck von P0 = 101.3 kPa. Die Anfangstemperatur des Arbeitsgases beträgt T1 = 310 K.
(a) Welcher Druck P1 herrscht im Gas zu Beginn des Prozesses (siehe Abbildung)?
(b) Welcher Druck P2 und welche Temperatur T2 herrschen im Gas am Ende des Prozesses?
(c) Wieviel Arbeit muss über den Ventilator zugeführt werden?
(d) Welcher Teil dieser zugeführten Energie leistet Arbeit am Kolben? Was passiert mit dem Rest?
m=80 kg
d=25cm
W
d=20 cm
2. Wärmekapazität [3 Punkte]
Ein einatomiges ideales Gas mit CV = 32 N kB durchläuft einen reversiblen Prozess entlang des Weges
P = aV b im P V -Diagramm, mit a > 0 und b konstant. Berechnen Sie die Wärmekapazität C =†Q/dT
für diese Prozessführung.
−b
Hilfe: Zeigen Sie, dass dV
gilt, mit einer noch zu bestimmenden Konstanten K. Zur Kontrolle
dT = KV
des Ergebnisses: Für b = 1 gilt für alle Werte von a, dass C = 2N kB ist.
3. Mikrokanonische Gesamtheit [4 Punkte]
Betrachten Sie N nicht wechselwirkende magnetische Momente in einem äußeren Magnetfeld
B. Die
PN
Mikrozustände des Systems r = (s1 , s2 , ..., sN ) mit sj = ±1 haben die Energie Er = μB j=1 sj . Berechnen Sie den Logarithmus der mikrokanonischen Zustandssumme ln Ω(U, N, B), und nähern Sie diesen
Logarithmus durch die Stirling-Formel.
Hilfe: Wählen Sie für den Energieunschärfeparameter ∆ = 2μB. Welchen Wert hat die innere Energie U ,
wenn genau n Momente parallel zu B ausgerichtet sind? Wieviele kombinatorische Möglichkeiten hierfür
gibt es? Nähern Sie die Fakultäten im Binomialkoeffizienten mit der Stirling-Formel ln k! ≈ k(ln k − 1).
Zeigen Sie, dass sich folgende Formel ergibt:
µ
¶
µ
¶
N μB + U
N μB + U
N μB − U
N μB − U
ln Ω(U, N, B) ≈ −
ln
−
ln
2μB
2N μB
2μB
2N μB
1
4. Schale eines hochdimensionalen Phasenraumvolumens [2 Punkte]
Für eine Kugel in n Dimensionen mit Radius R gilt VN (R) = CN RN . Schätzen Sie die Zahl der Zustände
in einer Kugelschale im Intervall (R − ∆R, R) für den Fall sehr großer Dimension N ab, wobei N = 1020
eine makroskopische Zahl sein soll. Nähern Sie das Ergebnis für großes Verhältnis zwischen Kugelradius
R
und Schalendicke ∆R
= n, wobei n zwar groß sein soll (z.B. n = 1000), aber n ¿ N gelten soll.
¡
¢n
Hilfe: Verwenden Sie für die Abschätzung die Euler-Formel 1 − n1 = e−1 .
2