Naturwissenschaften II (B. Sc. Maschinenbau) - IAP TU
Werbung

Übungen zur Vorlesung
Naturwissenschaften II
(B. Sc. Maschinenbau)
Sommersemester 2008
Musterlösung 4
Besprechung in der Woche
vom 12.5 - 19.5.08
Professor Dr. G. Birkl, Dr. N. Herschbach
www.physik.tu-darmstadt/apq/naturwissenschaften
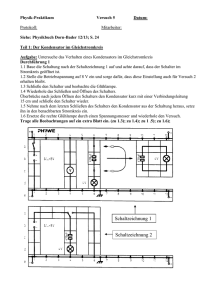
1. Kondensatornetzwerk
Wie groß ist die Gesamtkapazität der in der Abbildung gezeigten Schaltung? Es sei
C = 1 µF.
2C
2C
C/2
2C
C/2
C
2C
J̀
P
^
J́
Es gilt CGes = i Ci bei Parallelschaltung der Ci und CGes =
schaltung der Ci . Hier erhält man
"
C C
1
+ + +
C+
CGes =
2C
2
2
1
1
+
2C 2C
−1 #−1
≺./ •∞• ./
1
P
1
i Ci
−1
bei Reihen-
−1 −1 −1
1
+
= C = 1 µF.
2C
2. Ohmsches Gesetz in Praxis
Ein Stromverbraucher in der Industrie benötigt eine Gleichspannung UV von 6 kV bei
einer Stromstärke von 1.2 kA.
a) Welche Leistung wird dabei vom Industrieunternehmen verbraucht?
b) Wie groß ist der elektrische Widerstand RV des Verbrauchers?
c) Der Verbraucher wird über eine 7 km lange Zuleitung am Kraftwerk angeschloßen.
Die Zuleitung besteht aus Kupferdraht mit spezifischem Widerstand ρ = 1.7 ·
10−8 Ωm und einem Durchmesser von 5 cm. Bestimmen Sie den Widerstand RL
der Zuleitung.
d) Welche Spannung muß das Kraftwerk bereitstellen, damit beim Verbraucher 6 kV
zur Verfügung stehen?
e) Welche Stromdichte herrscht im Betrieb in der Zuleitung?
f) Der Ladungstransport duch die Kupferleitung wird durch die Beweglichkeit der
Elektronen mit Ladung e = −1.6 · 10−19 C gewährleistet. Es ist interessant die
Driftgeschwindigkeit vd der Elektronen in der Zuleitung im Betrieb zu berechnen.
Tun Sie dies und gehen Sie dabei von einer Ladungsträgerkonzentration nc =
8.4 · 1022 cm−3 aus.
J̀
^
J́
a) P = UV · I = 7.2 MW.
b) RV = UV /I = 5 Ω.
l
c) RL = ρ Al = ρ π(D/2)
2 = 60.6 mΩ.
d) Reihenschaltung der Widerstände RL und RV ergibt:
U = I(RL + RV ) = 6073 V.
e) j = I/A = I/(π(D/2)2 ) = 6.1 · 105 A/m2 .
f) Die Driftgeschwindigkeit vd der Elektronen hängt zusammen mit Stromdichte j
und Ladungsträgerdichte nc :
j = nc · q · vd = −nc · e · vd .
Hieraus ergibt sich
vd = − njc e = −45.5 µm/s.
≺./ •∞• ./
2
3. Moderne Fahrradbeleuchtung
Zur Erhöhung der Sicherheit wird im Rücklicht ein Kondensator mit einer Kapazität
C = 1 F eingebaut. Dieser Kondensator wird während der Fahrt über einen Widerstand
RC = 200 Ω mit dem vom Dynamo gelieferten Strom aufgeladen. Wenn die Fahrt
unterbrochen wird, kann die im Kondensator gespeicherte Energie genutzt werden,
um das Rücklicht noch eine Weile zu betreiben. Die Abbildung zeigt eine einfache
Schaltung, die hierzu benutzt werden kann. Das Licht wird von einer Leuchtdiode
P
RC
RLed
C
erzeugt, die wir als Verbraucher mit Widerstand RLed = 100 Ω betrachten. Wir gehen
davon aus, dass der Dynamo während der Fahrt für eine konstante Spannung U = 5 V
am Punkt P der abgebildeten Schaltung sorgt und dabei immer den nötigen Strom
liefert. Wenn die Fahrt unterbrochen wird und der Dynamo keinen Strom liefert, wird
der Punkt P der Schaltung vom Dynamo entkoppelt.
a) Welcher Strom muss der Dynamo zu Beginn der Fahrt liefern, wenn der Kondensator völlig entladen ist?
b) Wie lange brennt das Rücklicht noch nach dem Ende einer langen Fahrt, wenn
man davon ausgeht, dass die Leuchtdiode einen minimalen Strom von 2 mA zum
Leuchten benötigt?
J̀
J́
^
Laden und Entladen eines Kondensators
Herleitung der DGL: Spannung URC über Reihenschaltung von Kondensator C und
Q
+ IR ⇒ RQ̇ + C1 Q = URC .
Widerstand R ergibt URC = C
Lösung der homogenen DGL:
1
QH = 0
C
1
Q̇H
=−
⇒
QH
RC
t
⇒ ln(QH ) = −
+ Konstante
RC
t
⇒ QH (t) = k1 e− RC ,
RQ̇H +
mit k1 eine noch zu bestimmende Konstante.
3
Lösung der inhomogenen DGL: RQ̇ + C1 Q = URC
Ansatz: Q = QH + k2
1
1
⇒ RQ̇H + QH + k2 = URC
|
{z C } C
=0
⇒ k2 = CURC
t
⇒ Q(t) = k1 e− RC + CURC .
a) Kondensator ist nicht geladen: Q(0) = 0 und URC = U = 5 V ⇒ k1 = −CU .
Ausserdem ist R = RC = 200 Ω.
− t
⇒ Q(t) = CU 1 − e RC C
1
U −R tC
− t
⇒ I(t) = Q̇ = −CU −
e C
e RC C =
RC C
RC
U
⇒ I(0) =
= 25 mA (Kondensatorladestrom).
RC
Der vom Dynamo zu liefernde Gesamtstrom ist IGes =
U
RC
+
U
RLed
= 75 mA.
b) Kondensator ist geladen: Q(0) = CU = 5 C und URC = 0 V ⇒ k1 = Q(0) = CU .
Ausserdem ist R = RC + RLed = 300 Ω da beim Entladen die Leuchtdiode in
Reihe geschaltet ist.
⇒ Q(t) = CU e
− (R
t
C +RLed )C
⇒ I(t) = Q̇ = CU
=
1
−
(RC + RLed )C
t
U
−
e (RC +RLed )C
RC + RLed
!
e
− (R
t
C +RLed )C
= Imin = 2 mA
t
(RC + RLed )Imin
−
⇔ e (RC +RLed )C =
U
(RC + RLed )Imin
⇔ t = −(RC + RLed )C ln
= 636 s.
U
≺./ •∞• ./
4