Mechanik Aufgabe 1:Kinematik der Translation Das Diagramm 1
Werbung
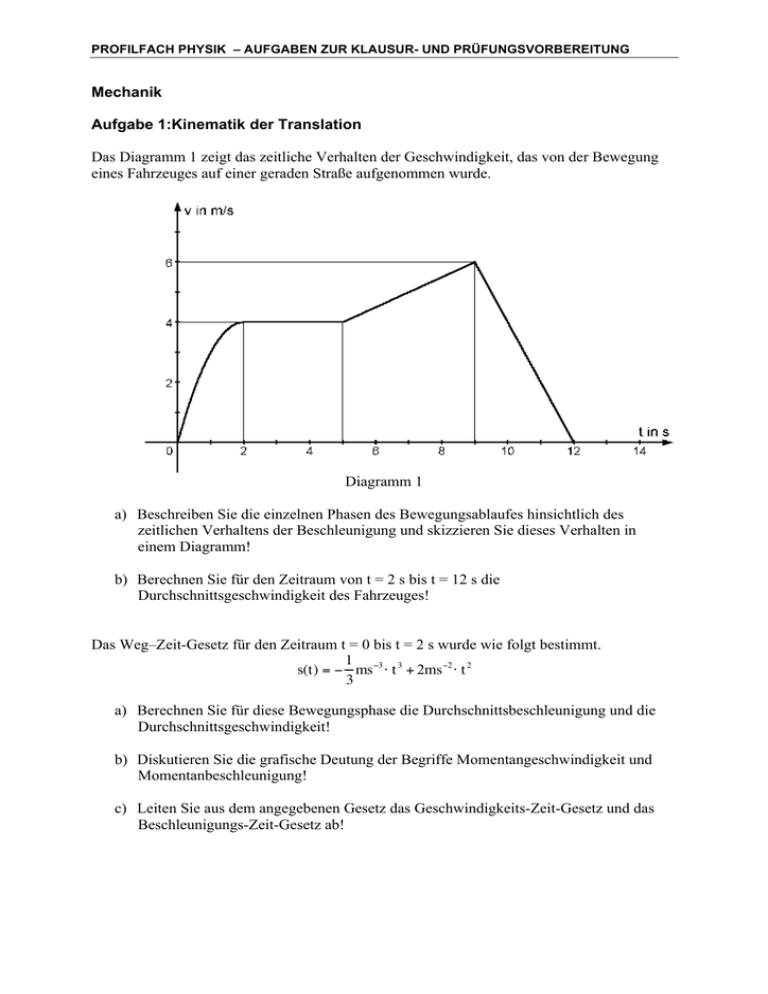
PROFILFACH PHYSIK – AUFGABEN ZUR KLAUSUR- UND PRÜFUNGSVORBEREITUNG Mechanik Aufgabe 1:Kinematik der Translation Das Diagramm 1 zeigt das zeitliche Verhalten der Geschwindigkeit, das von der Bewegung eines Fahrzeuges auf einer geraden Straße aufgenommen wurde. Diagramm 1 a) Beschreiben Sie die einzelnen Phasen des Bewegungsablaufes hinsichtlich des zeitlichen Verhaltens der Beschleunigung und skizzieren Sie dieses Verhalten in einem Diagramm! b) Berechnen Sie für den Zeitraum von t = 2 s bis t = 12 s die Durchschnittsgeschwindigkeit des Fahrzeuges! Das Weg–Zeit-Gesetz für den Zeitraum t = 0 bis t = 2 s wurde wie folgt bestimmt. 1 s(t) = − ms−3 ⋅ t 3 + 2ms −2 ⋅ t 2 3 a) Berechnen Sie für diese Bewegungsphase die Durchschnittsbeschleunigung und die Durchschnittsgeschwindigkeit! € b) Diskutieren Sie die grafische Deutung der Begriffe Momentangeschwindigkeit und Momentanbeschleunigung! c) Leiten Sie aus dem angegebenen Gesetz das Geschwindigkeits-Zeit-Gesetz und das Beschleunigungs-Zeit-Gesetz ab! PROFILFACH PHYSIK – AUFGABEN ZUR KLAUSUR- UND PRÜFUNGSVORBEREITUNG Aufgabe 2: Würfe a) Erläutern Sie mithilfe einer Skizze, aus welchen Bewegungsabläufen sich durch Überlagerung ein schräger Wurf ergibt! Stellen Sie hieraus die Bewegungsgesetze für die x- und die y-Richtung auf (Komponenten des Ortsvektors)! b) Leiten Sie aus den Komponenten des Ortsvektors die zeitfreie Bahngleichung des schrägen Wurfes her! c) Berechnen Sie den Abwurfwinkel und die Abwurfgeschwindigkeit eines schrägen Wurfes, wenn die Wurfhöhe 10 m und die Wurfweite 30 m betrug! Aufgabe 3: Newtonsche Axiome a) Formulieren Sie die Newtonschen Grundgesetze und erläutern Sie ihr Wirken anhand je eines Beispiels! b) Erklären Sie anhand eines selbst gewählten Beispiels den Unterschied zwischen Wechselwirkung und Kräftegleichgewicht! Aufgabe 4: Mathematische Grundlagen zur Kraft Gegeben seien zwei Kraftvektoren durch ihre Beträge F1 = 40 N und F2 = 60 N und den Winkel zwischen ihren Wirkungslinien α = 30°. a) Bestimmen Sie durch Konstruktion den Betrag des resultierenden Kraftvektors! b) Leiten Sie mit Hilfe Ihrer Konstruktion die angegebene Gleichung zur Berechnung des Betrages des resultierenden Kraftvektors her und bestätigen Sie die Konstruktion durch Berechnung! FR = F12 + F22 + 2⋅ F1 ⋅ F2 ⋅ cos α c) Ein 20 kg schwerer Körper ist symmetrisch an zwei Seilen aufgehängt. Bestimmen Sie die minimale Seilfestigkeit (in N), wenn der Winkel im Aufhängungspunkt zwischen € ist! den Seilen 120° d) Nennen Sie die physikalische Bedeutung der angegebenen Gleichungen und geben Sie eine geometrische Interpretation an! s2 dW (A) P = (B) W = F ⋅d s ∫ dt s1 € € PROFILFACH PHYSIK – AUFGABEN ZUR KLAUSUR- UND PRÜFUNGSVORBEREITUNG Aufgabe 5: Kräfte und Energiebilanzen bei Bewegungen a) Leiten Sie die angegebene Gleichung zur Bestimmung der energetischen Reibungsverluste bei einer Bewegung eines Körpers auf einer geneigten Ebene her! Geben Sie die Bedeutung der auftretenden Größen an! Begründen Sie Ihre Vorgehensweise mit Hilfe der Eigenschaften und der Wirkung von Reibungskräften! E therm = µ ⋅ m⋅ g⋅ h tan α In der Skizze (nicht maßstabsgerecht) ist folgender Vorgang dargestellt. € Ein Körper mit der Masse m = 5 kg wird mittels einer Feder auf eine Anfangsgeschwindigkeit vA = 10 ms-1 horizontal beschleunigt. Dabei beträgt die Spannstrecke der Feder 15 cm. Anschließend legt der Körper reibungsfrei eine Strecke von 8 m vom Punkt A bis zum Fußpunkt B der geneigten Ebene mit a = 20° zurück und bewegt sich dann (wiederum reibungsfrei) hangaufwärts bis zum Punkt C mit einer Höhe von h = 2 m über der Horizontalen. Dann kommt er auf der oberen Horizontalen im Punkt D infolge der jetzt auftretenden Reibung mit µ = 0,18 zur Ruhe. a) Beschreiben Sie die einzelnen Phasen des gesamten Vorgangs hinsichtlich der Art der Bewegung, der wirkenden Kräfte und der energetischen Umwandlungen! b) Berechnen Sie die Federkonstante der beschriebenen Feder! c) Berechnen Sie die Geschwindigkeit vC des Körpers im Punkt C! d) Berechnen Sie die Entfernung zwischen den Punkten C und D! e) Berechnen Sie die Werte für c) und d), wenn für die Strecken von B nach C und C nach D ein einheitlicher Reibungskoeffizient von µ = 0,09 angenommen wird! (Kontrollergebnis: vC = 7,15 ms-1)











