Übungen Aktivitätsanalyse und Kostenbewertung

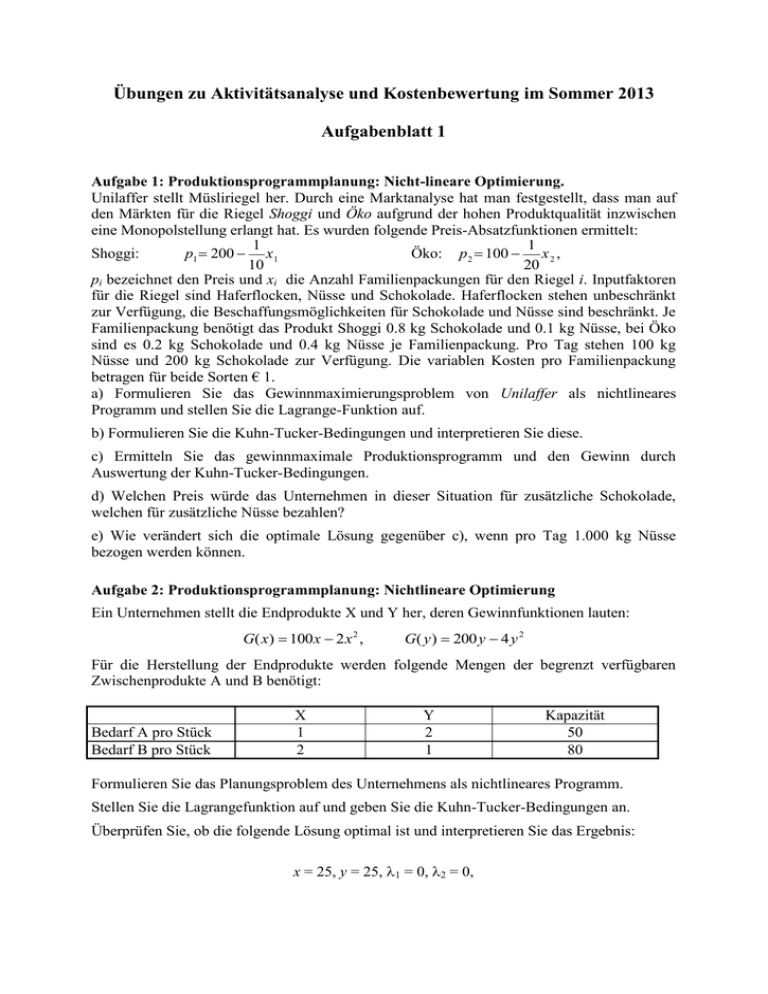
Übungen zu Aktivitätsanalyse und Kostenbewertung im Sommer 2013
Aufgabenblatt 1
Aufgabe 1: Produktionsprogrammplanung: Nicht-lineare Optimierung.
Unilaffer stellt Müsliriegel her. Durch eine Marktanalyse hat man festgestellt, dass man auf
den Märkten für die Riegel Shoggi und Öko aufgrund der hohen Produktqualität inzwischen
eine Monopolstellung erlangt hat. Es wurden folgende Preis-Absatzfunktionen ermittelt:
1
1
Shoggi:
Öko: p2  100  x 2 ,
p1  200  x1
10
20
pi bezeichnet den Preis und xi die Anzahl Familienpackungen für den Riegel i. Inputfaktoren
für die Riegel sind Haferflocken, Nüsse und Schokolade. Haferflocken stehen unbeschränkt
zur Verfügung, die Beschaffungsmöglichkeiten für Schokolade und Nüsse sind beschränkt. Je
Familienpackung benötigt das Produkt Shoggi 0.8 kg Schokolade und 0.1 kg Nüsse, bei Öko
sind es 0.2 kg Schokolade und 0.4 kg Nüsse je Familienpackung. Pro Tag stehen 100 kg
Nüsse und 200 kg Schokolade zur Verfügung. Die variablen Kosten pro Familienpackung
betragen für beide Sorten € 1.
a) Formulieren Sie das Gewinnmaximierungsproblem von Unilaffer als nichtlineares
Programm und stellen Sie die Lagrange-Funktion auf.
b) Formulieren Sie die Kuhn-Tucker-Bedingungen und interpretieren Sie diese.
c) Ermitteln Sie das gewinnmaximale Produktionsprogramm und den Gewinn durch
Auswertung der Kuhn-Tucker-Bedingungen.
d) Welchen Preis würde das Unternehmen in dieser Situation für zusätzliche Schokolade,
welchen für zusätzliche Nüsse bezahlen?
e) Wie verändert sich die optimale Lösung gegenüber c), wenn pro Tag 1.000 kg Nüsse
bezogen werden können.
Aufgabe 2: Produktionsprogrammplanung: Nichtlineare Optimierung
Ein Unternehmen stellt die Endprodukte X und Y her, deren Gewinnfunktionen lauten:
G( x)  100 x  2 x 2 ,
G( y )  200 y  4 y 2
Für die Herstellung der Endprodukte werden folgende Mengen der begrenzt verfügbaren
Zwischenprodukte A und B benötigt:
Bedarf A pro Stück
Bedarf B pro Stück
X
1
2
Y
2
1
Kapazität
50
80
Formulieren Sie das Planungsproblem des Unternehmens als nichtlineares Programm.
Stellen Sie die Lagrangefunktion auf und geben Sie die Kuhn-Tucker-Bedingungen an.
Überprüfen Sie, ob die folgende Lösung optimal ist und interpretieren Sie das Ergebnis:
x = 25, y = 25, 1 = 0, 2 = 0,
Aufgabe 3: Produktionsprogrammplanung: Nicht-lineare Optimierung:
Betrachten Sie das folgende nicht-lineare Problem:
max G  5x  25x 2  10y  100y 2
u.d.N.:
1
xb
2
xyc
x, y  0
Bezeichne  1 und  2 die Lagrangemultiplikatoren für die Nebenbedingungen (1) und (2).
a) Bestimmen Sie die unbeschränkte Lösung des Problems (d.h. die Lösung ohne die
Nebenbedingungen (1) und (2)).
x* =
y* =
G* =
b) Geben Sie die Untergrenzen b und c für b und c an, so dass die Lösung des unbeschränkten
Problems aus a) auch Lösung des beschränkten Problems ist.
b=
c=
c) Formulieren Sie die Lagrangefunktion für das beschränkte Problem.
L=
1
1
und c  sind folgende Elemente der optimalen Lösung bekannt: 1  0 ,
12
6
71
 2  0 und der maximale Gewinn G* 
. Was ist der optimale Wert für y?
144
d) Für b 
y* =
1
1
1
2
und c  ergibt sich als optimale Lösung x* 
und y* 
. Welche Werte
18
10
18
45
haben die Schattenpreise  1 und  2 im Optimum?
(Hinweis: Lösung durch Auswertung der Kuhn-Tucker-Bedingungen!)
e) Für b 
1 
2 