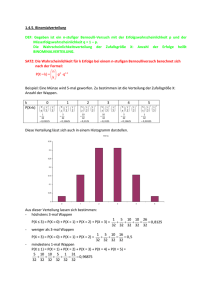
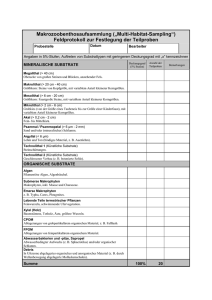
Frage: Antwort:

Frage:
Ich hab ne Frage zur Aufgabe 1. Und zwar weiß ich nicht welche Formel man
verwendet bei den Daten:
Beispiele:
Pp=0,5 (T > 60)
=
0, 0176 < 0, 05 = α
Pp=0,5 (T > 59)
=
0, 0284 < 0, 05
Pp=0,5 (T > 58)
=
0, 0443 < 0, 05
Pp=0,5 (T > 57)
=
0, 0666 > 0, 05
Antwort:
Man möchte bei dieser Teilaufgabe den Test finden, der die niedrigste Wahrscheinlichkeit für den Fehler 2. Art hat und zugleich die Niveau-α-Bedingung
einhält.
Das bedeutet man sucht die kritische Schranke ab der man sich für H1 entscheidet 1 .
Da die Binomialverteilung eine diskrete Verteilung darstellt wurde folgende Rechenregel verwendet:
k
X
P (X > k) = 1 − P (X ≤ k) = 1 − [
P (X = i)].
i=0
Mit:
P (X = k) =
n k
p (1 − p)n−k
k
Beispiel:
Sei X eine Binomialverteilte Zufallsvariable mit,
X ∼ B(5; 0, 5),
dann sind die Wahrscheinlichkeitsfunktion und die Verteilungsfunktion gegeben
durch:
k
P (X = k)
P (X ≤ k)
0
0,03125
0,03125
1
0,15625
0,1875
2
0,3125
0,5
3
0,3125
0,8125
4
0,15625
0,96875
5
0,03125
1
1 Skript Kapitel 16, S. 9 sowie Buch Toutenburg, H; Heumann, C; 2008; Induktive Statistik
- eine Einführung mit R und SPSS; Kapitel 7.2 und 4.2.5.
1
5
0, 50 0, 55 = 0, 03125
0
5
P (X = 1) =
0, 51 0, 54 = 0, 15625
1
P (X = 0) =
Ist man nun an der Wahrscheinlichkeit dafür interessiert, daß ein Erfolg öfter
als 2 mal eintritt, wird dies folgendermaßen berechnet:
P (X > 2)
=
1 − P (X ≤ 2) = 1 − [P (X = 0) + P (X = 1) + P (X = 2)]
=
1 − [0, 031225 + 0, 15625 + 0, 3125]
=
0, 5
oder
P (X > 2)
=
[P (X = 3) + P (X = 4) + P (X = 5)]
=
0, 3125 + 0, 15625 + 0, 03125
=
0, 5
Bezogen auf obige Aufgabe:
P (X > 60) =
100
X
P (X = i) = 1 −
60
X
P (X = i).
i=0
i=61
Dies wäre per Hand natürlich sehr aufwendig und wurde deshalb von uns per
Computer berechnet und angegeben.
2