5. Übung (Normalverteilung) Die Normalverteilung spielt eine sehr

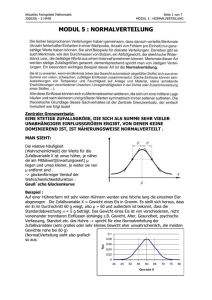
Vet. Med. Uni. Budapest
5. Übung
Biomathematik 2017
5. Übung (Normalverteilung)
Die Normalverteilung spielt eine sehr wichtige Rolle in den Biowissenschaften, unter
anderem auch in der Tiermedizin. Ihre Wichtigkeit beruht an dem sog. zentralen
Grenzwertsatz. Intuitiv kann man folgendes sagen. Die Summe einer großen Zahl von
unabhängigen Zufallsvariablen befolgt asymptotisch eine Normalverteilung bei endlicher
Varianz der Zufallsvariablen. Die statistischen Methoden nützen sehr oft aus, dass die
Versuchsdaten normalverteilt oder mindestens angenähert normalverteilt sind.
Normalverteilung
Die Normalverteilung kommt bei kontinuierlichen Zufallsvariablen vor.
Man stelle vor, dass das Körpergewicht von vielen Hühnern an einer Hühnerniederlassung
gemessen wird. Es wird eine Normalverteilung entstehen.
Die Inaugenscheinnahme der Normalverteilung
Frage: Es gibt eine Hühnerniederlassung. Was ist die Wahrscheinlichkeit dafür, dass die
Masse einer zufällig ausgewählten Huhne genau 1500, 1600 oder 1700 gramm. ist?
Antwort: Es ist einfach zu beantworten. Das Gebiet unter der Dichtefunktion in einem Punkt
(z.B. bei x=1500) ist immer Null. d.h. die Wahrscheinlichkeit dafür, dass eine stetige
Zufallsvariable einen konkreten Wert annimmt Null ist.
Im Falle einer diskreten Verteilung hat man einfach gezählt, was die Wahrscheinlichkeit der
einzelnen möglichen Werten. Im Falle einer stetigen Verteilung fallen die unendlich vielen
möglichen Werte in einem Intervall. Hier wird das Variationsbereich in Teilintervallen geteilt
und es wird gefragt, was ist die Wahrscheinlichkeit dafür, dass eine Beobachtung in einem
bestimmten Teilintervall einfällt.
Vom folgenden Menü kann man Kurven zeichnen:
Distribution/Continuous distributions/Normal distribution/Plot normal distribution
Die Normalverteilung hat zwei Parameter: der Erwartungswert (mü) und die
Standardabweichung (sigma). Die nennt man auch Lageparameter. Der Erwartungswert (mü)
bestimmt, wo der Mittelwert liegt. Es ist die höchste Stelle der Funktion und liegt auch in der
Mitte, die weil Normalverteilung symmetrisch ist. Die Streuung (sigma) gibt die Breite der
Funktion an.
Börzsönyi L.
1
Vet. Med. Uni. Budapest
5. Übung
Biomathematik 2017
Die drei vorhergehenden Normalverteilung sehen sehr ähnlich aus. Wenn man alle drei
Verteilungen auf einer Abbildung dargestellt, dann sieht man die Unterschiede. Wenn die
Streuung größer ist, dann ist die Dichtefunktion breiter und flacher. Wenn die Streuung
kleiner ist, dann ist die Dichtefunktion steiler und höher. Es ist eigentlich keine Überraschung,
nämlich das Gebiet unter der Dichtefunktion ist 1.
Rechenaufgaben
Frage: Es wird eine Rinderniederlassung mit 800 Kühen bezüglich der Michlaktation
beobachtet. Die durchschnittliche Milchproduktion der Kühe ist 32.625 Liter und die
Streuung ist 9.522 Liter ist. Wie viele Prozent der Niederlassung produziert weniger, als 28
Liter?
Antwort: Man nehme an, dass eine Normalverteilung vorliegt. Man gebe im Menü:
Distribution/Continuous distributions/Normal distribution/Normal Probabilities
Den Mittelwert und die Streuung. Sowie gibt man den Wert 28 an, nämlich es wird gefragt,
was ist die Wahrscheinlichkeit dafür, dass wie viel Prozent der Niederlassung weniger, als 28
Liter Milch gibt? Man kann im Programm wählen, dass man von der angegebenen Grenze (28
Liter) weniger (lower tail) oder größere (upper tail) Menge angeben möchte.
Börzsönyi L.
2
Vet. Med. Uni. Budapest
5. Übung
Biomathematik 2017
> pnorm(c(28), mean=32.625, sd=9.522, lower.tail=TRUE)
[1] 0.3135838
Die gesuchte Wahrscheinlichkeit wird in Output-Fenster erscheinen. In unserem Falle ist es
31.36%.
Frage: In der vorher erwähnten Niederlassung was ist die Wahrscheinlichkeit dafür, dass ein
Kuch zwischen 28 und 30 Liter Milch gibt?
Antwort: Man kann genauso verfahren wie vorher. Man nehme an, dass eine
Normalverteilung vorliegt.
Man gebe im Menü:
Distribution/Continuous distributions/Normal distribution/ Normal Probabilities
Den Mittelwert, die Streuung und die Wahrscheinlichkeit gibt man dafür an, dass die
Milchmenge mehr als 28 bzw. 30 Liter sein wird. Die Zahlen 28 und 30 muss man durch leere
Stelle trennen.
> pnorm(c(28,30), mean=32.625, sd=9.552, lower.tail=FALSE)
[1] 0.6858751 0.6082695
Die gesuchte Wahrscheinlichkeit kann man in Output-Fenster ablesen. Hier erscheinen wie
Werte. Man denke nach: Es gilt: P(28<X<30)=P(X<30)–P(X<28).
Die erste Wahrscheinlichkeit gibt an, dass die Milchproduktion mehr als, 28 Liter ist. Die
zweite gibt an, dass die Milchproduktion mehr als, 30 Liter ist. Die Differenz der zwei
Wahrscheinlichkeiten gibt dafür die Wahrscheinlichkeit an, dass die Milchmenge zwischen 28
und 30 Liter liegt. In Script-Fenster gibt man die Differenz einfach an:
> 0.6858751 - 0.6082695
[1] 0.0776056
Die gesuchte Wahrscheinlichkeit ist 7.76%.
Wenn man statt dem upper tail eben lower tail gewählt hätte, dann hätte man das selbe
Ergebnis mit negativen Vorzeichen bekommen.
Börzsönyi L.
3
Vet. Med. Uni. Budapest
5. Übung
Biomathematik 2017
Frage: Man möchte die schlechtesten 10% der Niederlassung bezüglich Milchproduktion
ausscheiden. Was ist die Minimale Milchproduktion, wobei ein Kuch noch in der
Niederlassung bleiben kann?
Antwort: Man nimmt an, dass eine Normalverteilung vorliegt. Im Menü
Distribution/Continuous distributions/Normal distribution/Normal Quantiles
Gibt man den Durchschnitt, die Streuung und die den Wert wofür die Wahrscheinlichkeit
berechnet wird.
> qnorm(c(0.1), mean=32.625, sd=9.552, lower.tail=TRUE)
[1] 20.38362
Nach diesem Ergebnis muss man alle Kühe, die unter 20.38 Liter produzieren, ausscheiden.
Frage: Was ist das auf dem Durchschnitt symmetrischen Intervall, in dem 95% der
Milchproduktionen einfallen? (Das ist ein Konfidenzintervall mit 95% Wahrscheinlichkeit um
den Mittelwert.)
Antwort: Man nimmt an, dass eine Normalverteilung vorliegt. Im Menü:
Distribution/Continuous distributions/Normal distribution/Normal quantiles
gibt man den Durchschnitt, Streuung und die entsprechende Wahrscheinlichkeit an. Wenn
man ein Konfidenzintervall mit 95% Sicherheit angeben will, dann erlaubt man 5% zu irren.
Wegen der Symmetrie halbiert man diese 5%, d.h. von beiden Seiten lässt man 2.5-2.5% weg.
Daraus folgt, man muss zu den 2.5% und 97.5% gehörenden Werte abfragen.
> qnorm(c(0.025,0.975), mean=32.625, sd=9.522, lower.tail=TRUE)
[1] 13.96222 51.28778
Man bekommt die Intervallgrenzen, die zu der 95% Sicherheit angehören, d.h. die
Intervallgrenzen um den Mittelwert sind 13.96 und 51.29. Mit anderen Worten, wenn man ein
Kuh von dieser Population ausgewählt wird, dann ihre Milchleistung fällt mit 95%
Wahrscheinlichkeit zwischen diesen Grenzen.
Börzsönyi L.
4
Vet. Med. Uni. Budapest
5. Übung
Biomathematik 2017
Relative Risk, Odds, Logit
Frage: Die folgende Tabelle zeigt das Vorkommen von Darmtumor in der verschiedenen
englischen Regionen1:
Region
Population
Fallzahlen
Cambridge
141264
19
Oxford
157658
21
Greenwich
220632
37
Wie groß ist das relative Risiko in Oxford bezüglich Cambridges?
Antwort: In beiden Region wird den Quotient von Fallanzahl und die ganze Population
berechnet (d.h. di Häufigkeit des Vorkommens) und Zahlen werden durcheinander geteilt.
RR=(21/157658)/(19/141264)=0.99
Frage: Wie groß ist das Odds des Tumors in den ersten zwei Region?
Antwort: das Odds ist die Wahrscheinlichkeit der Anzahl der positiven Fällen geteilt durch
die Wahrscheinlichkeit der Anzahl der negativen Fällen.
Cambridge: (19/141264)/((141264-19)/141264))=19/(141264-19)= 1,34518·10-4
Oxford: 21/(157658-21)= 1,332175·10-4
Frage: Wie groß ist der Logit des Tumors in den ersten Region?
Antwort: Der Logit ist ln Odds, d.h.
ln(1,34518·10-4) = -8.913813
Frage: Wie groß ist der Quotient von Odds in Oxford bezüglich Cambridge?
Antwort: Der Odds-Quotient ist 0.0001332175/0.000134518 = 0.9903321
1
0,99
http://www.guardian.co.uk/commentisfree/2011/oct/28/bad-science-diy-data-analysis
Börzsönyi L.
5