Feld einer ebenen Platte

.
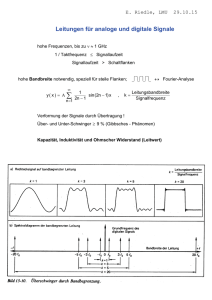
Feld einer ebenen Platte
G JG
F R
JG JG
E R
Elektrisches Feld
q
JG G
G
Rr
r d3r
U
JG G 3
4 S Ho
V Rr
1
³
G
für geladene Fläche mit Flächenladungsdichte V r gilt
JG G
G
Rr
V
r dA
JG G
4 S Ho R r 3
A
JG JG
E R
1
G
sei V r
³
JG
dE
V homogen:
³
A
V < dA G
b
4 S H o b2
1
horizontales Feld:
dEH
dE < sin D
vertikales Feld:
dE V
dE < cos D
es gilt:
dA
JG
dE
dM < r < dr
LMU
E. Riedle
E. Riedle
E2p
Physik
19.06.2007
.
2S f
EV
V
r
³ ³ 4 S H o b2 cos D < dr < dM
0 0
f
³
V
0 2 Ho a
S2
³
0
V
2 Ho
2
cos3 D < r < dr
sin D < dD
EV
EH
0
da
da
1
cos D
b
a
r
a < tgD
o
dr
a
dD
cos2 D
V
2 < Ho
aus Symmetriegründen
JG
E steht senkrecht zur Platte, unabhängig
vom Abstand a:
Feld homogen!
E. Riedle
LMU
Physik
.
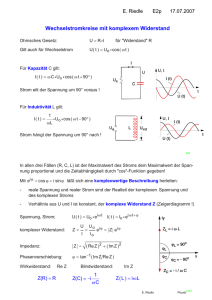
Endliche Abmessungen führen zu Randeffekten
besser zur Erzeugung eines homogenen Feldes:
Plattenkondensator mit
Q
dD
Q
JG
E
o
V G
x
Ho
Schutzring verbessert
Homogenität am Rand
LMU
E. Riedle
Physik
.
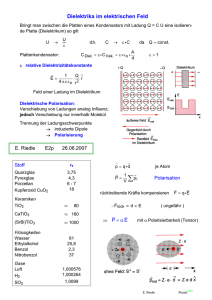
Geladene Hohlkugel
Flächenladungsdichte V ,
4 S R2 V
Q
Elektrischer Kraftfluß :
) el
³
JG JG
E < dS
³
divE < dV
Ÿ
JG
E
V S S
U
³
H
V S o
Q
4 S Ho r2
< dV
Q
Ho
r
entspricht Feld einer Punktladung Q im Mittelpunkt !
f
I r ³
Q
E < dr
4 S Ho r
r
JG
E r Ÿ
I r r
d.h., Feldstärke nimmt mit abnehmendem R zu !
o Spitzenentladung, Blitzableiter
für r < R gilt:
³
JG JG
E < dS
0
Ÿ
JG
E{0
Im Inneren der homogen geladenen Kugel herrscht kein Feld, I ist konstant !
E. Riedle
LMU
Physik
.
Geladene Vollkugel
Q
4
3
S R3 U
für r ! R :
JG
Er Q
4 S Ho r2
r
I r Q
4 S Ho r
für r d R
JG
Er Qr
4 S H o R3
r
I r §3
r2
¨ 4 S H o R ¨© 2 2R2
Q
·
¸
¸
¹
LMU
E. Riedle
Physik
E. Riedle
Physik
.
Geladener Stab
Koaxialkabel
JG
E
O
2 S Ho r
G
r
für
R1 d r d R2
OLadungsdichte pro Längeneinheit
LMU
.
Leiter im elektrischen Feld
Definition: Leiter sind Materialien, in denen elektrische Ladungsträger frei beweglich sind.
Auf frei bewegliche Ladungen wirkt
G
JG
F q<E
Kraft
o Verschiebung der Ladungen
o Aufbau eine Gegenfeldes,
das Feld kompensiert
Influenz
Das Innere von Leitern ist feldfrei !!!
Ladungen nur auf Oberfläche !!!
E. Riedle
LMU
Physik
.
Becher-Elektrometer
Löffeln von Ladungen !!!!
E. Riedle
LMU
Physik
.
Van-de-Graaff-Generator
6
Erzeugung von Spannungen bis 10 V
Faraday - Käfig
E. Riedle
Einführung in die Beschleunigerphysik
LMU
Physik
WS 2002/03
2.3.3 Der Van de Graaff-Beschleuniger
1930 begann Van de Graaff
mit der Entwicklung eines
Hochspannungsgenerators.
Unter normalen Bedingungen werden Spannungen bis
Umax = 2 MV
erzeugt. In einem Tank mit
Isoliergas (z.b. SF6) unter
einem Druck von ca. 1 MPa
sind Spannungen bis
Umax = 10 MV
möglich.
38
Einführung in die Beschleunigerphysik
WS 2002/03
5 MeV
Van-de-Graaff
am
Hahn-Meitner-Institut
in Berlin
39