Dielektrika im elektrischen Feld

.
Dielektrika im elektrischen Feld
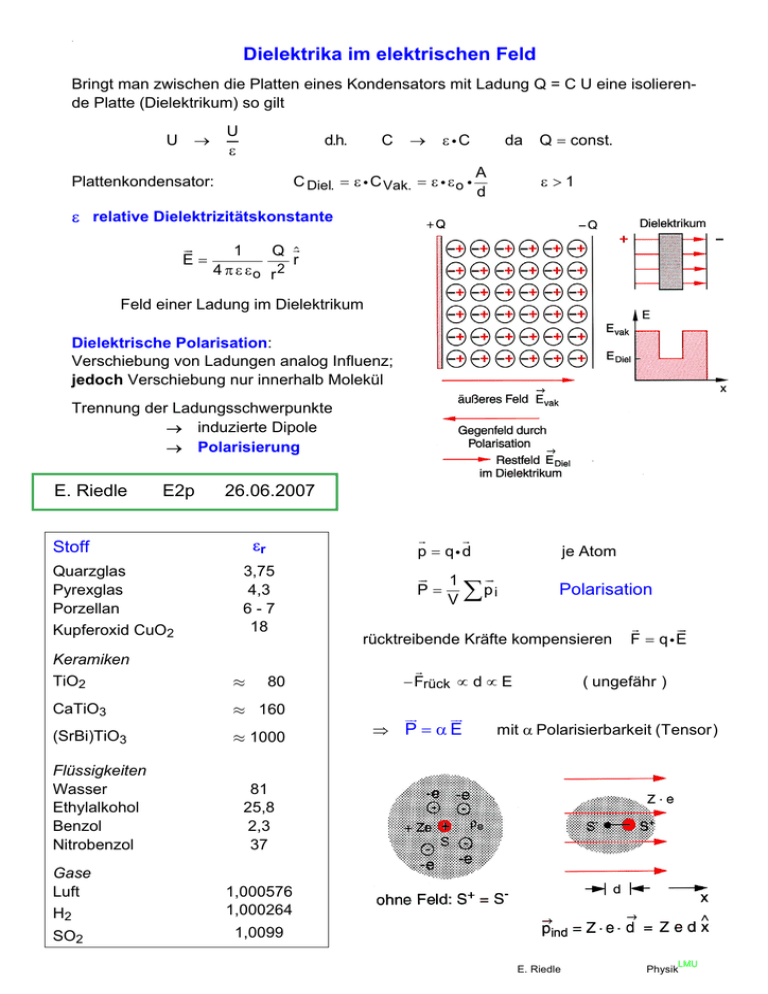
Bringt man zwischen die Platten eines Kondensators mit Ladung Q = C U eine isolierende Platte (Dielektrikum) so gilt
U
H
o
U
d.h.
Plattenkondensator:
C Diel.
C
o
H < C Vak.
H<C
H < Ho <
da
A
d
Q
const.
H !1
H relative Dielektrizitätskonstante
JG
E
1
Q G
r
4 S H Ho r2
Feld einer Ladung im Dielektrikum
Dielektrische Polarisation:
Verschiebung von Ladungen analog Influenz;
jedoch Verschiebung nur innerhalb Molekül
Trennung der Ladungsschwerpunkte
o induzierte Dipole
o Polarisierung
LMU
E. Riedle
E. Riedle
E2p
26.06.2007
.
Hr
G
p
G
q< d
3,75
4,3
6-7
18
JG
P
1
V
Stoff
Quarzglas
Pyrexglas
Porzellan
Kupferoxid CuO2
Keramiken
TiO2
x
CaTiO3
x 160
(SrBi)TiO3
Flüssigkeiten
Wasser
Ethylalkohol
Benzol
Nitrobenzol
Physik
JG
¦p i
Polarisation
rücktreibende Kräfte kompensieren
G
Frück v d v E
80
x 1000
je Atom

JG
P
JG
DE
G
F
JG
q<E
( ungefähr )
mit D Polarisierbarkeit (Tensor)
81
25,8
2,3
37
Gase
Luft
H2
1,000576
1,000264
SO2
1,0099
E. Riedle
LMU
Physik
.
unkompensierte Ladungen auf Stirnflächen
Polarisationsladungen:
Ladungsdichte
Qpol
A
Vpol
Qfrei
Ho
) el
"leerer" Kondensator:
N< q< d< A
A
JG
E Diel
mit Dielektrikum:
³
P
JG JG
E < dA
Polarisation
E<A

E
V
Ho
JG
JG
P
Evak Ho
Vfrei Vpol G
x
Ho
Feldstärke wird im Dielektrikum kleiner !!
JG
P
F
N< D
Ho
JG
N < D < E Diel
JG
H o < F < E Diel
dielektrische Suszeptibilität
JG
E vak. 1 JG

H 1 F
E vak.
H
1 F
JG
JG
JG
JG
H o < F < E Diel H o H1 E Diel H o E vak. E Diel
JG
E Diel
JG
P
E. Riedle
LMU
Physik
.
Gleichungen des elektrostatischen Feldes in Materie
homogenes Feld:
nur an der Oberfläche unkompensierte Polarisationsladungen,
1
d.h. Sprung von Evak. auf Evak.
H
inhomogenes Feld: auch im Inneren Polarisationladungen
' Q pol
³
Upol dV
V
³
Vpol dS
S

³
JG JG
P < dS
S
JJG
div P
³
JG
div P < dV
V
U pol
Durch äußeres Feld erzeugte Polarisationsladungen sind Quellen der elektrischen Polarisation !!!
JG
div E
U
Ho

JG
div E Diel
1
U frei U pol Ho
JG
§ JG
P ·
div ¨ E vak.
H o ¹¸
©
E. Riedle
LMU
Physik
.
dielektrische Verschiebungsdichte
JG
JG
JG
JG
D { H o < E Diel P H < H o < E vak.
JG
div D
U
U
mit
> D @ ¬ª H o E º¼ 1
Grenzfläche:
JG
H o H E Diel
o
As
U frei
1
m2
C
m2
JG
H o E vak.
Normalkomponente
JG
von D stetig
JG
Tangentialkomponente von D
nicht stetig
o
Brechungsgesetz
LMU
E. Riedle
Physik
.
Teilweise Einbringung des Dielektrikums in einen
Kondensator (mit Q const.) führt zur Verschiebung
von Ladung auf den Platten.
Q
C <U
Co < H < U
Elektrische Feldenergie im Dielektrikum
C
W el
w el
H<
o
1
CU2
2
Ho 2
<E
2
C<H
1
H H o E2 < A < d
2
1
E <D
2
allgemein !!
E. Riedle
LMU
Physik
.
Grund:
Zur Energiedichte 1 2 H o E2 im Vakuum addiert sich die Energie der Ladungsverschiebung.
d
W Pol
³ F dx
1 2
kd
2

W Pol
0
1
W
V Pol
w el
Q <E
d
k
1
Q <E < d
2
1
NpE
2
1
P <E
2
(pro Molekül)
1
p <E
2
1
H H 1 E2
2 o
Isolierter Kondensator mit Dielektrikum (Q konstant):
1
E D V
2 o o
W
1
E D V
2H o o
o
Differenz ist mechanische Energie !
E. Riedle
LMU
Physik
.
Kondensator mit Dielektrikum bei konstanter Spannung:
Kondensator wird weiter geladen !
W Batterie
'Q < U
H 1 Co U < U
1
H 1 Co U2
2
'W el
Energie fließt ins Dielektrikum
o mech. Kraft
Bei Flüssigkeit, die in den Kondensator gezogen werden
kann, ergibt sich ein Gleichgewicht.
W mech.
U fl < g < h < dV

l
h
'W el
1
H H 1 E2 dV
2 o
H o H 1 2
E
2 U fl < g
E. Riedle
LMU
Physik
.
Atomare Grundlagen
negative Ladungen: Elektronen
positive Ladungen:
Millikan-Versuch: q
Protonen
n < e
1) Schwerkraft = Auftriebskraft + Reibungskraft
o konstante Geschwindigkeit
2) elektrische Kraft = Schwerkraft
o
Ladung
o
o
Radius, Masse
Elementarladung
Ablenkung von Elektronen:
Beschleunigung o Parabelbahn
Brownsche Röhre, Lisajous – Figuren
LMU
E. Riedle
Physik
.
Molekulare Dipolmomente:
permanente Dipolmomente
induzierte Dipolmomente o Anlagerung an Ion
G
p
G
Q<d
1 Debye = 3,3356 x 10
E. Riedle
-30
Cm
LMU
Physik
.
Dipol-Dipol-Wechselwirkung o Anziehung
E. Riedle
LMU
Physik
.
Symmetrische Moleküle haben kein
permanentes Dipolmoment
Nur teilweise Ausrichtung im
elektrischen Feld ( Boltzmann ! )
E. Riedle
LMU
Physik