Rückkopplung und Stabilität eines dreistufigen Tran
Werbung

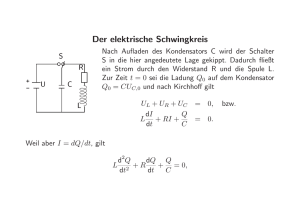
Dr.-Ing. Gottlieb Strassacker Dr.-Ing. Peter Strassacker Strassacker lautsprechershop.de Rückkopplung und Stabilität eines dreistufigen Transistorverstärkers 1. Theoretische Grundlagen 1.1 Einleitung In der Beschreibung ”die vier Rückkopplungsarten ....” werden die grundsätzlichen Möglichkeiten von Gegenkopplungsschaltungen an idealisierten Verstärkern (bei Niederfrequenz ohne Phasendrehung) gezeigt. Es werden dort mit Rücksicht auf die Übersichtlichkeit der Beschreibung, Phasendrehung und Instabilität von Verstärkern nicht besprochen. Dies soll hier nachgeholt werden. Um die Eigenschaften eines Verstärkers seinem Verwendungszweck entsprechend festzulegen, wird er bekanntlich in geeigneter Weise rückgekoppelt. Die Rückkopplung soll stabilisierend wirken, sie muß daher als Gegenkopplung ausgeführt werden. Da aber ein aus n Stufen bestehender Verstärker zwischen Ausgangs- und Eingangsspannung maximal n · 90o Phasendrehung aufweisen kann, wird eine Rückkopplung über alle n Stufen, für n ≥ 3 zwar bei Niederfrquenz als Gegenkopplung, bei hohen Frequenzen aber als Mitkopplung wirken können. Mitkopplung aber kann einen Verstärker instabil werden lassen, so daß er als Verstärker nicht mehr zu gebrauchen ist. Hier wird ein einfach rückgekoppelter Verstärker anhand der Ortskurve der Schleifenverstärkung auf Stabilität untersucht. 1.2 Verstärkung ohne und mit Rückkopplung Wir sprechen von einem Verstärkungsfaktor, wenn der Quotient aus gleichartigen Größen am steuernden Eingang und am gesteuerten Ausgang eine frequenzunabhängige Konstante ist oder bei konstanter Frequenz verstanden wird. Berücksichtigt man die Frequenzabhängigkeit v = v(ω), so ist dies korrekterweise eine Verstärkungsfunktion, obwohl man im Laborjargon auch sie oft unsauber als frequenzabhängigen Verstärkungsfaktor bezeichnet. Verwendet man die Symbolik der Regelungstechnik (mit nur einem Eingang und Ausgang an Stelle der je zwei Klemmen der Elektrotechnik), so gilt für das nicht rückgekoppelte System Bild 1. Wird dieser Verstärker rückgekoppelt, wobei der Rückkopplungsvierpol den reellen und frequenzunabhängigen Übertragungsfaktor k haben soll, (z.B. k1 bis k4 von der Beschreibung ”Die vier Rückkopplungsarten”), dann gilt: S St (ω) = S 1 (ω) ± S R (ω) (1) S R (ω) = ±k S 2 (ω) (2) S 2 (ω) = v o (ω) S St (ω) (3) v o (ω) = S 2 (ω) S 1 (ω) Bild 1: Verstärkung am nicht rückgekoppelten Verstärker v0 (ω) ist die Übertragungs– oder Verstärkungsfunktion ohne Rückkopplung. Bild 2: Rückgekoppeltes System Aus den Gln.(1) bis (3) erhält man mit v o (ω) = S 2 (ω)/S St (ω) die Übertragungsfunktion des Systems, die in unserem Fall eine Verstärkungsfunktion sein wird, zu: v R (ω) = S 2 (ω) v (ω) S St (ω) v o (ω) = o = S 1 (ω) S St (ω) ± S R (ω) 1 ± k v o (ω) (4) Man muß sich der Eindeutigkeit wegen entscheiden, ob im Nenner von Gl.(4) das Plus- oder das Minuszeichen gelten soll. Aus elektrotechnischer Sicht muß die Rückkopplung, beginnend bei Niederfrequenz, als stabilisierende Gegenkopplung wirken. Am Eingangsknoten von Bild 2 müssen also bei Niederfrequenz S 1 (ω) und S R (ω) gegenphasig summiert werden. Die Vorzeichenregelung in den Gleichungen korrespondiert ausschließlich mit der Bepfeilung der entsprechenden Schaltung. Siehe hierzu Bild 4a bis 4d der Anleitung: ”Die vier Rückkopplungsarten”. Läßt man am Eingangsknoten von Bild 2 nur das Pluszeichen zu, so gilt auch in Gl.(1) nur das Pluszeichen. Läßt man am Ausgangsknoten von Bild 2 ebenfalls nur das Pluszeichen zu, dann gilt in Gl.(2) nur das Minuszeichen. Allerdings tun wir Elektroingenieure uns mit der Bepfeilung und den zugehörigen Vorzeichen in Gleichungen oft leichter, wenn wir an unseren Vierpolen jeweils beide Eingangs– und Ausgangsklemmen mit ihren Spannungs– und Strombezugspfeilen zeichnen: Siehe Bild 4. Dagegen hat die in der Regelungstechnik gängige Bepfeilung nach Bild 2 den Vorteil, neutral zu sein bezüglich der rückgeführten Größe (Strom oder Spannung) und der Art der Addition am Eingang (Serien- oder Parallelschaltung). Wir betrachten nachfolgend das Beispiel Spannungsverstärker. Da v o (ω) bei Niederfrequenz wegen Gegenphasigkeit von S 1 und S 2 einen negativen Zahlenwert repräsentiert, wählen wir die Bezugspfeile des Bildes 4 so, daß im Nenner von Gl.(4) das Minuszeichen gilt und schreiben, indem wir auch weiterhin komplex rechnen: v o (ω) v R (ω) = (5) Logarithmiert man nun Gl.(5), so erhält man: 20 log v R (ω) = 20 log v o (ω) − 20 log(1 − k v o (ω)) oder 20 log u (ω) u (ω) u2 (ω) = 20 log 2 − 20 log(1 − k 2 ) u1 (ω) uSt (ω) uST (ω) (6) (7) Daraus folgen für den Betrag die (logarithmischen) ”Verstärkungsmaße”: |v R (ω)| |v (ω)| |1 − k v o (ω)| = 0 − dB dB dB (8) mit einer Amplitudenabnahme von: 60 dB dvR ≤ dω Dekade bei einem dreistufigen Verstärker. Für die Phasenwinkel gilt: ϕR (ω) = ϕo (ω) − ϕ(1 − k vo (ω)) (9) und speziell wieder für den dreistufigen Verstärker: ϕR (ω) − ϕR (ω = 0) ≤ 2700 Das Entstehen der Phasendrehung wird in der Beschreibung ”Phasenkompensation” ausführlich besprochen. Gl.(8) läßt sich am Amplitudengang, hier am Bodediagramm nach Bild 3, gut veranschaulichen. Bild 3: Bodediagramm eines dreistufigen Verstärkers Man erkennt aus Gl.(8): In logarithmischen Maßen ist von der Verstärkung ohne Rückkopplung bei Niederfrequenz vo der Anteil 1 − k · vo abzuziehen, damit man das bei Gegenkopplung wirksame Verstärkungsmaß vR erhält. 1.3 Der Begriff der Schleifenverstärkung Unter Schleifenverstärkung wird nachfolgend die spezielle Übertragungsfunktion V (ω) verstanden. Sie entsteht durch Auftrennen der Rückkopplungsschleife (hier bei A – A’) und Messen der Verstärkung, die in der Schleife herum vorhanden ist. Das heißt, Multiplikation des Rückkopplungsfaktors K mit der Verstärkungsfunktion v 0 (ω) des Verstärkers. Man hat dann uaa0 = u02 als Eingangsgröße und ubb0 = u2 als Ausgangsgröße der Schleife, wobei die Klemmen 1 – 1’ kurzzuschließen sind: û û û ûbb0 = 2 = 2 · St = v o k u = V (ω) Es ist ûaa0 û20 ûSt û20 Bild 4: Verstärker in Parallel–Parallel–Gegenkopplung Es ist der Spannungsverstärkungsfaktor ohne Rückkopplung: v o = û2 /ûSt und der Rückkopplungsfaktor: k u = ûSt /û20 bei Kurzschluß an 1 – 1’. Der Kurzschluß der Klemmen 1 – 1’ ist notwendig, da die Einspeisung bei a – a’ erfolgt, andererseits aber der normale Betriebszustand mit Wirkung des Generatorinnenwiderstandes RG amm Verstärkereingang erhalten bleiben muß. 1.4 Stabilitätsbetrachtung am rückgekoppelten System Verstärker müssen stabile Systeme sein. Da sie aber gesteuerte Quellen (Operationsverstärker, Transistoren) enthalten, kann durch Rückkopplung die Voraussetzung zur Instabiltät gegeben sein. Will man also einen Verstärker gegenkoppeln, so muß man ihn auf seine Stabilität hin untersuchen. • Allgemeine Definition: Ein Verstärker ist dann stabil, wenn er nach einer beliebigen Störung in endlicher Zeit wieder in seinen stationären Ruhezustand übergeht. Zur Untersuchung der Stabilität eines Übertragungssystems wird eine Prüffunktion benötigt, deren Nullstellen und Pole (Eigenwerte) je nach ihrer Lage in der komplexen Frequenzebene über die Stabilität des komplexen Systems entscheiden. Eine derartige Prüffunktion ist hier die Funktion 1 − V (s) = 0 mit s = σ + jω. Die in den Eigenwerten enthaltenen Pole der Verstärkungsfunktion v R der Gleichung (5) erhält man durch Nullsetzen der Nennerfunktion 1 − V (s) = 0. Dazu muß die in Gl.(5) enthaltene reelle Frequenz jω ersetzt werden durch die komplexe Frequenz s = σ + jω. Nochmals: Die Pole von v R erhält man aus den Nullstellen der Nennerfunktion 1 − V (s) = 0. Die Lage dieser Pole von v R in der komplexen Frequenzebene entscheidet über die Stabilität des untersuchten Verstärkers. Es gilt: • Ein einfach rückgekoppelter Verstärker ist nur dann stabil, wenn die Ortskurve der Schleifenverstärkung V (jω) den Punkt (+1, 0) bei zunehmender Frequenz nicht rechtswendig umschlingt. Geht man nämlich von der komplexen Frequenz– oder s–Ebene (Bild 5a) über zur Ebene der komplexen Schleifenverstärkung V (Bild 5b), so besteht zwischen beiden Ebenen eine konforme Abbildung. In der s–Ebene sind σ und ω, in der V –Ebene ReV und ImV die Variablen. Alle Eigenwerte von 1 − V (s) = 0 werden in der V –Ebene im Punkt (+1, 0) abgebildet. Die Abbildung der positiven jω–Achse der s–Ebene ist die Ortskurve V (ω). Nach den Regeln der konformen Abbildung gilt hier: • Durchläuft man die positive jω–Achse der s–Ebene im Sinne wachsender ω, so entspricht dies in der V –Ebene dem Durchlaufen der Ortskurve V (ω) ebenfalls mit wachsendem ω. Da alle Pole von v R in den Punkt (+1, 0) der V –Ebene abgebildet werden, weiß man aus seiner Lage links oder rechts von der V (ω)–Ortskurve, ob in der s–Ebene Pole von v R links oder rechts von der Frequenzachse liegen, ob also ein Übertragungssystem stabil oder instabil ist. Das Übertragungssystem sei ein einfach (im Gegensatz zu mehrfach) rückgekoppelter Verstärker. Auf Grund seiner inneren Beschaltung hat er, wie die meisten Verstärker, eine Grundphasendrehung von 1800 zwischen Ausgangs– und Eingangsspannung. Die Ortskurve beginnt daher auf der negativen reellen Achse bei ω1 . Zu diesen 1800 addiert sich eine mit der Frequenz negative Phasendrehung ∆ϕ(ω). Ihr Betrag nimmt mit der Frequenz zu, so daß die Ortskurve vom Punkt (-1, 0) aus im Uhrzeigersinn dreht. Diese Phasendrehung wird innerhalb der einzelnen Verstärkerstufen durch je einen unvermeidlichen Tiefpäß erzeugt. Drei Verstärkerstufen bringen daher eine zusätzliche maximale Phasendrehung von ∆ϕ = −2700 . 5a: komplexe Frequenzebene 5b: Ortskurve der Schleifenverstärkung Bild 5: Konforme Abbildung der jω–Achse in die V –Ebene Für eine bestimmte Kreisfrequenz ω2 schneidet die Ortskurve die positive reelle Achse. In diesem Punkt ω2 ist die Gesamtphasenverschiebung zwischen uaa0 und ubb0 , also die Phasenverschiebung der Schleifenverstärkung nach Bild 6, gerade 00 . Das heißt: Ausgangsspannung und Eingangsspannung der aufgetrennten Schleife (beide an der Schnittstelle bei A – A’) sind gleichphasig. Bei geschlossener Schleife wäre dies echte Mitkopplung für Spannungen mit der Frequenz ω2 . Bei geschlossener Schleife soll der Verstärker jedoch stabil bleiben! Um dies zu erreichen, muß ûbb0 kleiner sein als ûaa0 bei Gleichphasigkeit dieser beiden Spannungen, also im Punkt ω2 von Bild 5b. Dies bedeutet: Bei Gleichphasigkeit von Ausgangs– und Eingangsspannung muß |V (ω)| < 1 sein. Diese Forderung stimmt mit der oben hergeleiteten überein, daß die Ortskurve den Punkt (+1, 0) nicht rechtswendig umschlingen darf. Falls außer der Phasenbedingung auch die genannte Betragsbedingung für Instabilität: |V (ω)| > 1 erfüllt wäre, könnte der Verstärker bei geschlossener Schleife Schwingungen mit der Kreisfrequenz ω2 erzeugen, er würde als Generator wirken! Die Instabilität könnte auch so groß sein, daß das Ausgangspotential des Verstärkers nach dem Einschalten der Versorgungs– Gleichspannungen sprunghaft zur einen oder zur anderen Aussteuerungsgrenze hinschnellen würde. 1.5 Wirksamer Spannungsverstärkungsfaktor bei Rückkopplung Analog zu den allgemeinen Systemgleichungen (1) bis (3) gelten mit den Bezugspfeilen von Bild 6 die Beziehungen: Ausgangsspannung Steuerspannung Eingangsstrom Rückkopplungsstrom Steuerstrom û2 = v0 ûSt ûSt = û1 − î1 RG î1 = îSt − îR îR = (û2 − ûSt )/RR îSt = ûSt /RSt (10) (11) (12) (13) (14) Mit den Gleichungen (10) bis (14) erhält man nach Bild 6 , bei wirksamer Rückkopplung zwischen Eingangs- und Ausgangsspannung, den wirksamen Spannungsverstärkungsfaktor v R oder v uR zu: Bild 6: Ströme und Spannungen am Gesamtverstärker bei wirksamer Rückkopplung vR = û2 = û1 1+ v0 RG RSt + RG (1 RSt − v0) = v0 1 + a − k v0 (15) Die Konstanten a und k sind der Gleichung (15) entnehmbar: a= RG RG + RSt RR und k = RG RR Um v R von den inneren Eigenschaften des Verstärkers, also von Schwankungen der Verstärkung v 0 weitgehend unabhängig zu machen, ist man bestrebt,eine möglichst wirksame Gegenkopplung anzuwenden. Dadurch erreicht man für Meßverstärker hohe Genauigkeit und zeitliche Konstanz der wirksamen Verstärkung v R . Es soll also sein: vR v0 . Damit wird aus Gl.(15): −1 = reell und unabhängig von v 0 (16) vR ≈ k 1.6 Ersatzbild für den aufgetrennten Verstärker Trennt man den Gesamtverstärker nach Bild 6 an der Stelle A – A’ auf und schließt man die Eingangsklemmen 1 – 1’ kurz, so erhält man durch Umzeichnen die Schaltung nach Bild 7, als Meßschaltung für die Ermittlung der Schleifenverstärkung. Mit û2 = v 0 ûSt und dem Spannungsteiler RR /(RG ||RSt ) zwischen û02 und û1 erhält man die Schleifenverstärkung: G v 0 (ω) · R û2 k v0 RR V (ω) = 0 = RG RG = û2 1+a 1 + RR + RST (17) Bild 7: Schaltung zur Messung der Schleifenverstärkung V (ω) Gl.(18) drückt V (ω) durch die gleichen Größen aus, die auch in Gl.(15) enthalten sind. Der Vergleich dieser beiden Gleichungen ergibt: vR = v0 (1 + a)[1 − V (ω)] (18) Man entnimmt Gl.(19), daß 1 − V (ω) die Eigenwerte (Pole) von v R (ω) enthält. Der Prüfpunkt ist (+1, 0) und nicht ((1 + RG /RSt + RG /RR ), 0), wie man nach Gl.(15) annehmen könnte. Ersetzt man in 1 − V (ω) die variable jω durch s = σ + jω, so erhält man die im Abschnitt 1.4 schon genannte Prüffunktion 1 − V (s). Es ist also festzustellen, ob 1 − V (s) = 0 Lösungen mit positivem Realteil hat. Hierzu gibt es analytische und experimentelle Methoden. Die analytische Methode kann nur dann angewandt werden, wenn die Schleifenverstärkung tatsächlich als gebrochen rationale Funktion vorliegt. Diese Funktion aufzustellen würde aber erfordern, daß außer allen Werten der konzentrierten Bauelemente auch Schalt- und Diffusionskapazitäten, Leitungsinduktivitäten und alle Nichtlinearitäten bekannt wären und in die Berechnung der Schleifenfunktion einbezogen würden. Ein solcher Rechengang ist nur sehr aufwendig durchzuführen. Viel einfacher ist die Messung. 1.7 Vorbereitung von Messungen der Schleifenverstärkung Bei der Messung muß der Verstärker stabil sein. Man muß daher, wie wiederholt gesagt wurde, die einzig vorhandene Rückkopplung auftrennen und zwar an einer günstigen Stelle, so daß sich dadurch die Übertragungs– oder Betriebseigenschaften des Verstärkers nicht verändern. Dies ist der Fall an der Stelle A – A’ nach Bild 6. Dabei entstehen die Klemmenpaare a – a’ und b – b’mit den zugehörigen Abschlußwiderständen Z b und Z a . Man müßte nun das Klemmenpaar b – b’ mit einem Widerstand Z a , den man nach a – a’ hin sieht, abschließen. Ebenso müßte das Klemmenpaar a – a’ mit einem Widerstand Z b , den man nach b – b’ hin sieht, abgeschlossen werden. Der Verstärkereingang 1 – 1’ ist kurzzuschließen, da RG den bei Normalbetrieb vorhandenen Generatorwiderstand ersetzt. An die Ausgangsklemmen 2 – 2’ ist der Lastwiderstand anzuschließen. Eingespeist wird die Schaltung am Anschluß a – a’ des Rückkopplungsvierpols mit der Spannung u02 (t). Die Anschlüsse b – b’ sind identisch mit dem Verstärkerausgang 2 – 2’. Damit läßt sich V (ω) als Verhältnis von ûbb0 zu ûaa0 messen. ———————————————————————————————————————— Literaturhinweis: Auszug aus dem früheren ”Praktikum für analoge und digitale Messtechnik” des Instituts für Theoretische Elektrotechnik und Messtechnik der Universität Karlsruhe, Verfasser Dr.-Ing. Gottlieb Strassacker und Mitarbeiter.