¨Ubung zum Elektronikpraktikum Blatt 3
Werbung

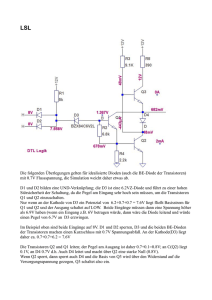
Universität Göttingen Prof. Dr. Arnulf Quadt [email protected] Sommersemester 2010 Raum D1.119 Übung zum Elektronikpraktikum Blatt 3 13. September - 1. Oktober 2010 1: Allgemeine Beschreibung des Operationsverstärkers Schon beim einfachen Transistor wurde gezeigt, dass man durch Gegenkopplung zwar den Verstärkungsfaktor herabsetzt, dafür aber erhebliche Vorteile erhält. Beispielsweise erhöht sich die thermische Stabilität und die Verstärkung wird im wesentlichen durch die gegenkoppelnden Elemente bestimmt. Herstellungsbedingt Schwankungen von Transistoreigenschaften spielen also keine Rolle mehr. Dementsprechend wünscht man sich für den universellen Einsatz in verschiedenen Schaltungen Verstärker mit speziell gezüchteten Daten derart, dass die Eigenschaften der Schaltung ausschließlich durch das jeweils rückkoppelnde Netzwerk bestimmt werden. Da durch geschickte äußere Beschaltung dieser Verstärker u.a. diverse mathematische Operationen elektronisch realisiert werden können, heißen sie Operationsverstärker (Operational Amplifiers: OA). 1) Ein OA hat zwei Eingänge, einen invertierenden (U− ) und einen nichtinvertierenden Eingang (U+ ). Schaltsmbol: U− − Ua U+ + Er verhält sich als Differenzverstärker, d.h. es gilt: Ua = V0 · (U + −U− ). (1) 2) Hohe Leerlaufverstärkung: Der Leerlaufverstärkungsfaktor V0 ist in der Größenordnung V0 = 104 ...106 . 3) Verschwindender Eingangstrom: praktisch erreicht man Werte für I+ und I− von 200 nA für OAs mit Bipolartransistoren und 30 pA, falls die Eingänge mit Feldeffekttransistoren bestückt sind. Zusätzlich fordert man aus praktischen Gründen noch eine Reihe weiterer Eigenschaften, die z.T. auch für normale Gleichspannungsverstärker gelten. Dazu gehören: 4) Kleiner Ausgangswiderstand, d.h. die Ausgangsspannung ist unabhängig von der Last. Praktische Werte sind Ra = 50 Ω ... 1 kΩ. 5) Kein Offset; für U+ = U− = 0 sollte nach Gleichung (1) Ua = 0 sein. Praktisch ist das jedoch nicht der Fall, sondern man muss eine kleine “Offset”-Spannung von einigen mV zwischen die Eingänge legen, um Ua = 0 zu erreichen. 6) Hohe Gleichtaktunterdrückung. Legt man an + und - die gleiche spannung Ugl , U+ = U− = Ugl = 0, so sollte nach Gleichung (1) (abgesehen vom Offset) ebenfalls Ua = 0 gelten. Praktisch tritt jedoch eine Gleichtaktverstärkung auf: Vgl := ∆UA 6= 0. ∆Ugl (2) Man gibt sie in der Form der “Gleichtaktunterdrückung” g = von 104 − 106 erreicht werden. V0 Vgl an, für die Werte Natürlich braucht ein OA eine Betriebsspannung, die man meist symmetrisch um Erde halbiert. Die Ausgangsspannung Ua kann dann positive und negative Werte annahmen. +U B + − U− − Ua U+ + − + −UB Gegenkopplung Spannungsgegenkopplung (nicht invertierenden Verstärker) Ue + Ua − Z1 Z2 U+ = Ue ; U− = Ua · Z1 /(Z1 + Z2 ) Ua = V0 · (U+ − U− ) Ua = V0 · Ue /(1 + k · V0 ) (3) (4) (5) dabei ist k := Z1 /(Z1 + Z2 ) der Bruchteil der zurückgekoppelten Ausgangsspannung Ua . Für die Spannungsverstärkung v := Ua /Ue erhält man v = V0 /(1 + k · V0 ) = 1/(1/V0 + k). Ist nun die Spannungsverstärkung V0 ≫ k, so gilt v = 1/k = 1 + Z2 /Z1; die Spannungsverstärkung des gegengekoppelten OA wird unabhängig von den spezielle Kennwerten des OA. Eingangswiderstand Re und Ausgangswiderstand Ra der Gesamtschaltung sind nicht identisch mit den Werten des unbeschalteten OA. Man kann vielmehr zeigen (siehe z.B. TietzeSchenk), dass sie durch die Gegenkopplung noch um die sogenannte Schleichverstärkung g = k · V0 verbessert werden. Man erhält typischerweise: Re = 109 ...1014 Ω Ra = 0.1...0.01 Ω (6) (7) Stromgegenkopplung (invertierender Verstärker) Z2 Ue Z1 − Ua + U+ = 0; U− = (Ua − Ue ) · Z1 /(1 +Z2 ) + Ue Ua = −V0 · Ue /(1 + k · (1 + V0 )); (8) (9) dabei ist hier k = Z1 /Z2 der Rückkopplungsfaktor. Für die Spannungsverstärkung v = Ua /Ue erhält man v = −V0 /(1 + k · V0 ) = −1/(1/V0 + k), da V0 ≫ 1 immer erfüllt ist. Ist nun die Leerlauf-Spannungverstärkung V0 ≫ k, so gilt v = −1/k = −Z2 /Z1 ; die Spannungsverstärkung des stromgekoppelten OA wird ebenfalls unabhängig von den speziellen Kennwerten des OA. Da der nicht invertierende Eingang geerdet ist, liegt auch der zweite Eingang praktisch bei Null. Man bezeichnet solch einen Punkt als “virtuelle Erde”, virtuell deswegen, weil keine galvanische Verbindung mit der Masse vorliegt. Ist Ie der Eingangsstrom, so gilt für die Ausgangsspannung Ua = −Z2 · Ie . Die Schaltung verhält sich so, also ob der Eingangsstrom von der virtuelle Erde aus über die Impedanz Z2 zum Ausgang fließt. Ausgangswiderstand: Wie beim nicht-invertierenden Verstärker. Eingangswiderstand: Wegen der virtuellen Erdung gilt Re = Z1 . Damit ist Re erheblich kleiner als der Eingangswiderstand des OA selbst. ⇒ Frage 5A: Warum kann man diesen Nachteil nicht einfach dadurch beheben, dass man für Z1 beliebig hohe Werte einsetzt? (z.B. Z1 = 1010 Ω, Z2 = 1011 Ω für V = 10). Anwendungen Beispiele für frequenzunabhängige Gegenkopplung a) Differenzverstärker R2 R1 U1 − Ua U2 + R1 R2 Aus U1 −U− R1 = U− −Ua ; U− R2 = U+ = R2 R1 +R2 · U2 folgt Ua = R2 R1 · (U2 − U1 ). ⇒ Frage 5B: Was geschieht, wenn beide R1 und beide R2 untereinander nicht ganz gleich sind? b) Addierer Aus U− = U+ = 0 I− = 0 (10) (11) U2 Un Ua U1 + + ... + = − . R1 R2 Rn R0 (12) folgt U1 U2 Un R0 R1 − R2 Ua Rn + Für R1 = R2 = ...Rn =: R gilt: Ua = −R0 /R · (U1 + U2 + ... + Un ). c) Stromquelle R1 UL RL IL U1 − + U+ = 0 → Ua U1 Ua =− = IL R1 RL (13) Eine Stromquelle soll bekanntlich einen konstanten Strom unabhängig von der Last RL abgeben. Das ist beim idealen OA in obiger Schaltung offensichtlich der Fall, denn IL = U1 /R1 6= f (RL ) (14) ⇒ Frage 5C: Der differentielle Innenwiderstand Ri := dUL /dIL einer idealen Stromquelle ist ∞. Berechnen Sie den tatsächlichen Innenwiderstand obiger Schaltung, indem Sie zwar weiterhin I− ≪ IL annehmen, jedoch V0 = 105 berücksichtigen. (Es ist also nicht mehr U− = 0!) (Ergebnis: Ri = V0 · R1 ). Der Innenwiderstand Ri hängt also bei gegebenem V0 ausschließlich von R1 und nicht vom Strom IL ab. ⇒ Frage 5D: Ist diese Schaltung für einseitig geerdete Verbraucher geeignet? Beispiele für frequenzabhängige Gegenkopplung a) Differenzierer IR R C Ue IC − Ua + Für solche Schaltungen gibt es zwei äquivalente Betrachtungsweisen: a) im Zeitbereich: Man sucht den zeitlichen Zusammenhang zwischen Ua und Ue . Wegen U− = U+ = 0 gilt für den Kondensator Q = C · Ue , also IC = Q̇ = C · U̇e , I− = 0 → IC = IR C · U̇e = −Ua /R → Ua = −RC · U̇e (15) (16) (17) b) im Frequenzbereich: Man sucht den frequenzabhängigen Zusamenhang zwischen Ua und Ue . Setzt man beide komplex an: Ue = Ue0 · expiωt ; Ua = Ua0 · expi(ωt+φ) , (18) so kann man mit der Formel des invertierenden Verstärkers sofort die komplexe Verstärkung V (ω) = Ua /Ue = −R/(1/iωC) = −iω · RC (19) und den Frequenzgang des Amplitudenverhältnisses V (ω) = Ua0 /Ue0 = ωRC (20) angeben. Für die Phase φ zwischen Ua und Ue gilt: tan φ → −RC/0 → −∞ → φ = −π/2 (21) Setzt man in V (ω) den komplexen Ansatz für Ue ein, so erhält man Ua = −iωRC · Ue = −RC · U̇e , (22) wie gehabt. Bei Differenzierern steigt demnach die Verstäkung proportional zu ω (= 6 db/Oktave) an. b) Integrierer C IC Iin IR Ue R’ − R Ua E + Im Punkt E gilt: IR > IC + Iin . a) Zeitgang: Iin ∼ 0; IR = IC IC = −C U˙a → Ua = −1/RC · IR = UR /R; (23) Z Ue dt (24) b) Frequenzbereich −1 +i Ua = iωC = Ue R ωRC 1 Ua0 = ; V (ω) = Ue0 ωRC tan φ = +∞ → φ = π/2; V (ω) = 1 iωt aus R Ua = − iωRC Ue folgt durch Einsetzen von Ue = Ue0 · exp wieder Ua = Ue dt. (25) (26) (27) (28) −1 RC · Bei Integratoren fällt also die Verstärkung umgekehrt proportional zu ω (= −6 dB/Oktave) ab. In der Praxis kann bei Integratoren der Offset des OA sehr stören, da er aufintegriert wird und Ua schnell eine der Aussteuerungsgrenzen erreicht. Um dem zu begegnen, kann man den Offset kompensieren oder durch einen Widerstand R′ parallel zu C die Integration niedriger Frequenzen verhindern. c) Resonanzverstärker (selektive Filter) R2 C L R1 Ue − Ua + V Ua =− Ue = 1/ 1 R2 + 1 iωL + iωC R1 (29) ⇒ Frage 5D: Zeigen Sie: a) Die Verstärkung erreicht ein Maximum VRES = R2 /R1 bei der Resonanzfrequenz 1 ωRES = √LC . b) Die Güte der Resonanzkurve ist Q = R2 q C L = R2 . ωL Beispiele für nicht-lineare Gegenkopplung a) Logarithmischer Verstärker ID R Ue − Ua + Hier liegt ein Bauteil mit nichtlinearer Strom-Spannungskennlinie in der Rückkopplung vor. Für Dioden gilt in Durchlassrichtung außerhalb des Anlaufbereichs ID = K1 · exp(K2 UD ), (30) wobei K1 und K2 Konstanten der jeweiligen Diode sind. Aus U− = U+ = 0 und I− = 0 folgt Ue /R = ID = K1 · exp(−K2 Ua ); Ua = 1/K2 · ln(Ue /K1 R) ⇒ Frage 5E: Wodurch wird die Genauigkeit der Schaltung begrenzt? b) Exponentialverstärker (31) R Ue ID − Ua + Aus U− = U+ = 0; I− = 0 folgt ID = −Ua /R; ID = K1 · exp(K2 Ue ), und weiter Ua = −R · K1 · exp(K2 Ue ) (32) (33) c) Präzisionsgleichrichter Die an einen idealen Gleichrichter gestellte Forderung Ua = Ue Ua = 0 für Ue > 0 für Ue ≤ 0 (34) (35) wird von einer einfachen Diode zumindest für kleine Ue nicht erfüllt, da entsprechend ihrer Kennlinie stromabhängig mehr oder weniger Spannung an ihr abfällt. Ein OA kann diesen Nachteil ausgleichen. R R Ue − + Ua U’a Für Ue > 0 wird Ua′ < 0, d.h. D1 sperrt, D2 leitet. Es gilt Ue /R = −Ua /R → Ua = −Ue . Der entsprechend ihrer Kennlinie an D2 auftretende Spannungsabfall (Ua′ − Ua ) wird vom OA automatisch erzeugt, da er für den Rückkopplungszweig R−D2 als Stromquelle wirkt. Für Ue < 0 wid Ua′ > 0, d.h. D1 leitet, D2 sperrt. Weiterhin gilt U− = U+ = 0 und, da D2 sperrt, gilt auch Ua = 0. Mitgekoppelte Schaltungen Bei Mitkoppung wird ein Teil der Ausgangsspannung so auf einen der Eingänge zurückgeführt, dass Änderungen von Ua über die Rückkopplung noch verstärkt werden. Vergleichen Sie z.B. folgende Schaltungen: Ue + Ua − a) Ua = Ue · V0 /(V0 + 1) Ue − Ua + b) Ua = Ue · V0 /(V0 − 1) In beiden Fällen existiert zu gegebenem Ue also ein Ua , das die Gleichung des Differenzverstärkers löst. ⇒ Frage 5F: Was passiert, wenn Ua (durch Störung oder weil Ue sich geändert hat) kurzzeitig von “erlaubten” Wert abweicht? Beachten Sie, dass die Signallaufzeit durch den OA nicht verschwindend gering ist. Welche Schaltung ist gegen- und welche mitgekoppelt? In mitgekoppelten Schaltungen nähert sich Ua demnach i.A. mit hoher (hauptsächlich vom internen Aufbau des OA bestimmten) Geschwindigkeit einer der beiden Aussteuerungsgrenzen. Typisch beträgt die Anstiegsrate 0.5...15 V/µs. Wenn eine Aussteuerungsgrenze erreicht ist, bestehen zwei wesentliche Unterschiede zu allen bisherigen Schaltungen: a) Es gilt nicht mehr U+ = U− , sondern zwischen beiden Eingängen kann eine beliebige Spannungsdifferenz auftreten. b) Ua hängt von UB (Betriebsspannung) ab. Bisher trat UB in den Formeln für Ua nie auf. In der Praxis is Ua eine schwache Funktion von UB . Jedoch werden Schwankungen in UB (z.B. überlagerter Brumm) stark (mit typisch 90 db) unterdrückt. Dies gilt natürlich nicht an den Aussteuergrenzen. Beispiele a) Invertierender Schmitt-Trigger Ue − +U B Ua + −U B R2 R1 Bei konstanter Eingangsspannung Ue sitzt Ua wegen der Mitkopplung an einer der beiden Aussteuerungsgrenzen. Sobald Ue jedoch bestimmte Potentiale (Schalt-Schwellen Ue1 , Ue2 ) über- oder unterschreitet, kippt Ua zur jeweils anderen Grenze hinüber. obere Schwelle untere Schwelle Schalthysterese Ue1 = Ua,max · R1 /(R1 + R2 ) Ue2 = Ua,min · R1 /(R1 + R2 ) ∆U = Ue1 − Ue2 . (36) (37) (38) Für Ue > Ue1 (Ue < Ue2 ) wird also Ua = Ua,min (Ua = Ua,max ). Und für Ue1 ≥ Ue ≥ Ue2 bleibt Ua , wo es gerade ist. Anwendung: Signalformung, z.B. Erzeugung eines Rechtecks definierter Amplitude aus einem verrauschten Sinus. b) Astabiler Multivibrator R − C Ua + R2 R1 Führt man beim invertierenden Schmitt-Trigger Ua über einen Tiefpass auf den “-”Eingang zurück, werden beide Grenzlagen instabil. Durch auf- bzw. Entladung des Kondensators überschreitet U− die jeweils wirksame Schaltschwelle und Ua kippt mit einer durch τ = RC bestimmten Frequenz ν zwischen den Grenzlagen hin und her. ⇒ Frage 5G: Zeigen Sie: T = 1/ν = 2RC · ln(1 + 2R1 /R2 ) gilt bei symmetrischen Grenzen (Ua,min = −Ua,max ). Anwendung: Rechteckoszillator, Blinkerschaltungen usw. c) Monostabiler Multivibrator (Monoflop) R − C Ue C’ + Ua R2 R1 Die Diode verhindert hier eine Aufladung des Kondensators C auf Spannungen kleiner −UD , wobei UD die Durchlassspannung der Diode ist. Falls die durch R1 , R2 bestimmte untere Schaltschwelle tiefer liegt, befindet sich Ua demnach an der negativen Aussteuerungsgrenze in einem stabilen Zustand. Ein positiver Impuls über C ′ auf den “+”-Eingang lässt Ua zur oberen Grenze kippen, wo sie für die Zeit T ∼ RC · ln(1 + R1 /R2 ) für UD ≪ Ua,min bleibt. Anwendung: Impulsformung, Zeitschalter, Verzögerungsglieder. 2: Schaltungen mit Operationsverstärkern • In den folgenden Schaltungen wird ein Operationsverstärker als Impedanzwandler für eine 10 V (Spitze-zu-Spitze !!) sinusförmige Spannung verwendet. Der Operationsverstärker weist einen maximalen Ausgangsstrom von 20 mA auf. Bestimmen Sie den Spannungsverlauf über dem Lastwiderstand R2 und stellen Sie diesen graphisch dar. Ue + − + V1 5V 1000 Hz 0 Deg Ua − R2 100 Ohm • In den folgenden Schaltungen wird ein Operationsverstärker als Impedanzwandler für eine 10 V (Spitze-zu-Spitze !!) sinusförmige Spannung verwendet (wie oben). Der Operationsverstärker weist einen maximalen Ausgangsstrom von 20 mA auf. Die drei Schaltungen unterscheiden sich durch die nachgeschaltete Endstufe, die den Ausgangsstrom erhöhen soll. 1) In der Schaltung wird eine Class-B Endstufe dem OA nachgeschaltet. Diese besteht aus den komplementären Transistoren Q1 (npn) und Q2 (pnp). Beide Transistoren sind in Kollektorschaltung aufgebaut. a) Bestimmen Sie das Ausgangssignal an Widerstand R2 als Funktion der Zeit. Überlegen Sie sich hierzu, wann welcher der beiden Transistoren Strom leitet. Zeichnen Sie das Signal und markieren Sie den Leitungszustand der Transistoren in dem Graphen. b) Wie viel Strom fließt maximal durch die Transistoren? Wie sieht der Strom als Funktion der Zeit aus? VCC 10 V Q1 Ue + − V1 5V 1000 Hz 0 Deg + Ua R2 − 100 Ohm Q2 VDD −10 V 2) Die Class-B Endstufe wird durch einen Widerstand zwischen Basis und Emitter der Transistoren erweitert. Hierdurch liefert bei kleinen Spannungen der Operationsverstärker den Ausgangsstrom und erst bei höheren Spannungen werden die Transistoren aktiv. a) Bestimmen Sie die Spannung an R2 für kleine Amplituden. Nehmen Sie hierzu an, dass die Transistoren ignoriert werden können, da sie noch sperren. b) Bestimmen Sie R1, so dass die Transistoren bei einem Ausgangsstrom (durch R2) von 10 mA anfangen zu leiten (idealisierte Basis-EmitterSpannung). Bei welcher Eingangsspannung Ue fangen die Transistoren an zu leiten? c) Bestimmen Sie die Spannung über R2 für das oben angegebene sinusförmige Eingangssignal. Tragen Sie die Ausgangsspannung als Funktion der Zeit auf. Beachten Sie besonders den Bereich des Nulldurchgangs und den Bereich, an dem die Transistoren den Strom übernehmen! Wie groß ist der maximale Strom durch den Transistor? VCC 10 V Q1 Ue + − V1 5V 1000 Hz 0 Deg + R1 Ua R2 − 100 Ohm Q2 VDD −10 V 3) In den beiden obigen Schaltungen fließt durch die Transistoren kein Strom, wenn kein Signal am Eingang anliegt. Um die Probleme um den Nulldurchgang des Signals zu minimieren, kann eine Class-AB Endstufe hinter den Operationsverstärker geschaltet werden. Hierbei sorgt eine Vorspannung der Basis-Emitter Diode für einen Ruhestrom durch die Transistoren. Diese sind damit bereits im leitenden Zustand (siehe Blatt 2). Nehmen Sie im Folgenden an, dass ein Ruhestrom (Eingangssignal = 0 V) von 1 mA durch die Transistoren fließt. a) Wie groß ist im Ruhezustand die Spannung an der Basis der beiden Transistoren? b) Wie groß ist die Spannung an den Basen und am Emitter für eine Eingangsspannung von Ue = 2 V bzw. Ue = −2 V? c) Bestimmen Sie die Ausgangsspannung für das oben angegebene sinusförmige Eingangssignal und zeichnen Sie dieses als Funktion der Zeit. d) Zeichnen Sie den Strom durch die Transistoren als Funktion der Zeit. Zeichnen Sie für jeden Transistor einen eigenen Graphen. VCC 10 V R1 1.0 kOhm Q1 Ue + − V1 5V 1000 Hz 0 Deg + D1 − D2 Ua R3 100 Ohm Q2 R2 1.0 kOhm VDD −10 V