Lineare Antennen

HFT-Praktikum I
Lineare Antennen
LA/1
Lineare Antennen
In einem nicht drahtgebundenen Übertragungssystem übernehmen Antennen die Aufgabe, ein von der
Senderstufe geliefertes Signal (Leitungswelle) in eine Freiraumwelle zu wandeln bzw. diesen Vorgang wieder umzukehren.
1. Leitungsnäherung
Man kann sich eine einfache Dipolantenne als aus einander geklappte, offene Zweidrahtleitung vorstellen.
Die Stromverteilung wird zunächst sinusförmig angenähert; am offenen Ende ergibt sich ein Stromknoten.
Durch die gestreckte Struktur bleibt das Feld nicht mehr auf ein kleines Gebiet beschränkt, sondern füllt
weite Bereiche des Raumes aus. Dadurch kann es den sehr schnellen Änderungen des Stromes und der
Ladung nur in unmittelbarer Antennennähe folgen, weiter entfernte Bereiche lösen sich ab.
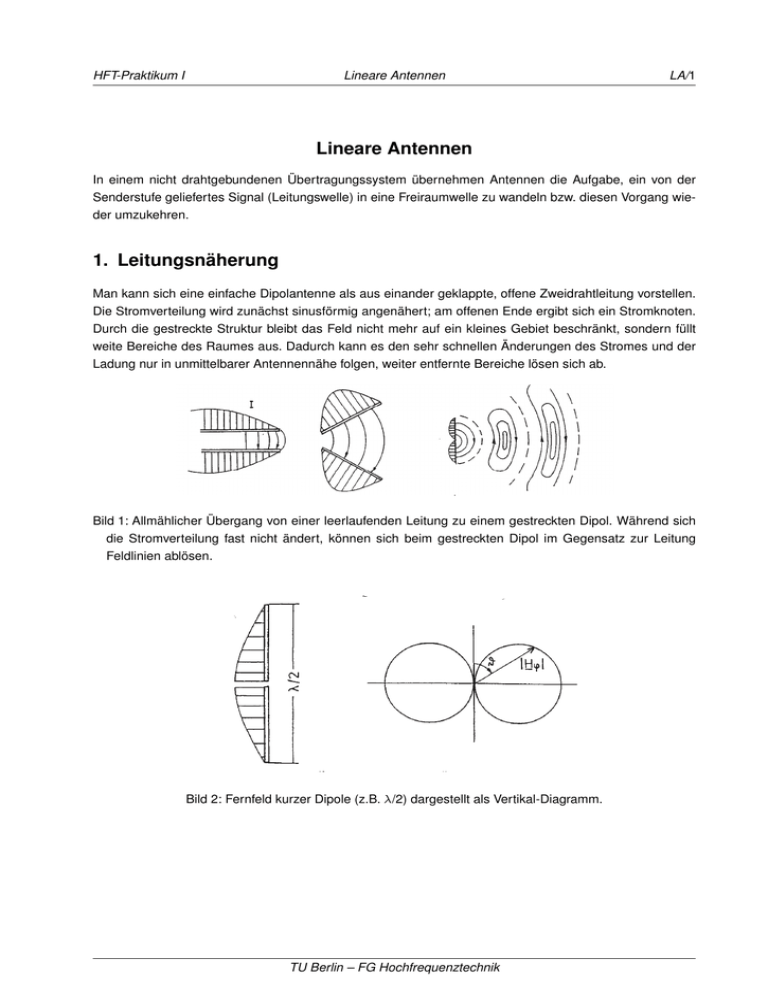
Bild 1: Allmählicher Übergang von einer leerlaufenden Leitung zu einem gestreckten Dipol. Während sich
die Stromverteilung fast nicht ändert, können sich beim gestreckten Dipol im Gegensatz zur Leitung
Feldlinien ablösen.
Bild 2: Fernfeld kurzer Dipole (z.B. /2) dargestellt als Vertikal-Diagramm.
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/2
2. Fernfeld
Die Berechnung des Fernfeldes erfolgt über eine Integration der Stromverteilung auf der Antenne unter Berücksichtigung der durch den Wegunterschied r hervorgerufenen Phasenverschiebung ' =
Az (~r) =
e
jk0 r
Zh
0
4r I (z )e
jk0 r (z
0
) dz 0
k 0 r ( z ) .
(1)
h
r = z 0 cos #
H ' = jk0 sin #Az
E # = H ' ZF 0
Bild 3: Stromverteilung und Fernfeldberechnung der Antennenlänge h
Es ist leicht zu sehen, dass sich der Ausdruck Az (z ) für r = 0 zu einer Integration von I (z ) vereinfacht.
Bei Längen h = n ergibt sich deshalb eine Nullstelle in der Horizontalen (so z.B. beim 2-Dipol).
Bild 4: 2-Dipol, Stromverteilung, V-Diagramm, Abstrahlung.
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/3
3. Fußpunktimpedanz
Die Leitungsnäherung ergibt für die Impedanz im Speisepunkt (Z F ) einen rein imaginären, cotangensförmigen Verlauf.
Bild 5: Blindwiderstand und U/I-Verteilung auf einer idealen offenen Leitung.
In der komplexen Ebene verliefe die Ortskurve von Z F (h) dann nur an der imaginären Achse.
Bild 6: Z F (h)-Ortskurve für diverse Schlankheitsgrade (nach King [3]).
In der Praxis ergibt sich die in Abb. 6 dargestellte Impedanzkurve, die dem Verhalten einer verlustbehafteten
Leitung ähnelt ([1], Kap. WEL). Diese Verluste existieren tätsächlich, weil die Antenne Energie abstrahlt.
Der Durchmesser der Impedanzschleife hängt vom Schlankheitsgrad 2h=a der Antenne ab (a = Antennenradius). Je dünner die Antenne ist, desto höher sind die in Leiternähe auftretenden Feldstärken bzw.
Energiedichten. Die damit zusammenhängende zusätzliche Speicherung von Blindenergie führt zu der Aussage, dass dünne Antennen eine höhere Güte (geringere relative Verluste) aufweisen als dicke Antennen
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/4
(Bild 7).
Die Folge endlicher Antennendicke zeigt sich im Richtdiagramm, wo aus Nullstellen relativ flache Minima
werden und Nebenzipfel weniger deutlich hervortreten. Außerdem ist zu beobachten, dass die Resonanzpunkte für die gezeigten Schlankheitsgrade nicht auf der reellen Achse liegen, was sich erst für sehr hohe
Werte , z.B. 2h=a 1000, ergeben würde.
Bild 7: Zusätzlich mit We ; Wm erfülltes Volumen (elektrische bzw. magnetische Energie).
Im Folgenden wird nur noch von Monopolen (halbe Dipole) die Rede sein, die man durch Einführen einer
leitenden Fläche in der Speiseebene erhält. Das Verhalten ist analog zu Dipolen, nur sind Fußpunktwiderstand und Spannungen (z.B. aus Abb. 6) zu halbieren.
4. Resonanzfrequenzen
Der Imaginärteil der Fußpunktpunktimpedanz verschwindet für bestimmte Frequenzen. Man spricht dann
von Resonanz. Das geschieht immer dann, wenn die Antennenlänge – bzw. doppelte Antennenlänge bei
Monopolen – ungefähr einem ganzzahligen Vielfachen der halben Wellenlänge entspricht:
2h = n 2
mit n
2 f1; 2; 3; 4 : : : g:
Die erste Resonanz ergibt sich für Monopole also bei h
(2)
= res =4, wofür man über = c0 =f
die dazu
gehörige Resonanzfrequenz ermitteln kann:
fres ;1
= 4ch0
(3)
Die weiteren Resonanzen treten bei ganzzahligen Vielfachen dieser Frequenz auf. Da bei jeder weiteren,
höheren Frequenz die Stromverteilung entlang der Antenne eine andere ist, ergeben sich auch unterschiedliche Abstrahlcharakteristiken bzw. Sendeleistungen. Der Realteil der Fußpunktimpedanz berücksichtigt die
abgestrahlte Leistung der Antenne und hat somit bei den verschiedenen Längen andere Werte. Tabelle 1
zeigt nach [4] die ungefähren Längen der Antenne bei den ersten Resonanzen und die dazu gehörenden
Realteile der Fußpunktimpedanz.
Hierbei wurden der Strahlungswiderstand R0
= 75 log10
h
2a
und der Korrekturfaktor F 0
TU Berlin – FG Hochfrequenztechnik
= 1+h=ah=a verwendet.
HFT-Praktikum I
Lineare Antennen
LA/5
Tabelle 1: Längen und Fußpunktimpedanzen eines Monopols bei seinen ersten vier Resonanzen [4].
Länge h
1. Resonanz
2. Resonanz
3. Resonanz
4. Resonanz
34
R 2
48
R 2
0; 24 F 0
ZF
0; 48 F 0
0; 72 F 0
0
34
0; 96 F 0
0
48
5. Dachkapazität
In der Praxis wird vielfach die Maßnahme getroffen, durch eine Dachkapazität die Resonanzfrequenz einer
Antenne zu senken. Hierdurch lassen sich Antennen geringerer Bauhöhe realisieren bzw. dieselben bei
tieferen Frequenzen (größeren Wellenlängen) betreiben. Realisiert werden Dachkapazitäten z.B. in Form
von aufgesetzten Scheiben.
Bild 8: Monopol mit Dachkapazität.
Der Einfluss der Dachkapazität lässt sich anhand eines im oberen Bereich geknickten Monopols verdeutlichen:
Die Stromverteilung setzt sich auf dem horizontalen Stück fort. Die Randbedingung I (L) = 0 (am Ende) gilt
weiterhin, der Stromverlauf sei immer noch ungefähr sinusförmig. Die erste Resonanz (h~
bei
h + h =
res
4 :
=
) liegt dann
4
(4)
Generell lässt sich die durch die Dachkapazität hervorgerufene, scheinbare Verlängerung der Antenne um
h folgendermaßen bestimmen:
Da
h
h = 4res
h:
(5)
auf jeden Fall kleiner ist als =4 und kurze (offene) Leitungen sich kapazitiv verhalten, hat das
verlängernde Element den Charakter einer Kapazität. Deren Größe lässt sich aus den Leitungsgleichungen
herleiten.
Der Antenne wird ein Leitungswellenwiderstand zugeordnet, der sich näherungsweise aus dem Schlankheitsgrad ergibt:
ZA = 60
ln(1; 15h=2a):
(6)
Der Scheinwiderstand am Punkt 2 lautet
ZE
= jZA cot( h); = 2=:
TU Berlin – FG Hochfrequenztechnik
(7)
HFT-Praktikum I
Lineare Antennen
LA/6
Bild 9: Ersatzschaltbild für eine Dachkapazität.
Gleichsetzen mit der Impedanz der Kapazität Z E
= j!C1 D
führt zu dem Ausdruck
h ) h
= tan(
!Z = cZh ;
!ZA
A
0 A
der einen Wert für die Dachkapazität CD liefert, wenn h aus der Resonanzfrequenz bestimmt wurde.
CD
(8)
6. Strahlungsgekoppelte Elemente
Im Nahfeld eines 2 -Dipols existiert eine nicht zu vernachlässigende Ez -Komponente. Ein weiterer, in der
Nähe angebrachter (Parasitär-)Stab von ungefähr derselben Länge verursacht eine Störung, weil auf seiner
Oberfläche die genannte Ez -Feldstärke auf Grund der Randbedingungen für ideale Leiter nicht existieren
darf. Bei offenen Klemmen des Parasitärstabs äußert sich dies in einer Leerlaufspannung, die sich aus dem
Nahfeld des ersten Dipols ergibt.
Die Abhängigkeit von U2 ; I2 lässt sich durch Vierpolparameter darstellen:
!
!
!
Z 11 Z 12
I1
U1
=
(9)
Da die Klemmen des 2. Stabes im allgemeinen kurzgeschlossen sind (U2
= 0), ergibt sich für das Verhältnis
U2
Z 21 Z 22
der beiden Fußpunktströme:
I2
I1
I2
)
= ZZ21 ((d=
22 h=)
(10)
Die Addition der von den jeweiligen Strömen in horizontaler Richtung in großem Abstand erzeugten Feld-
stärken führt auf den sog. Gruppenfaktor M ('; #), der die gemeinsame Wirkung der Antennen beschreibt.
Das gesamte Fernfeld in beliebige Raumrichtungen ergibt sich durch Multiplikation mit der Charakteristik
des Einzelstrahlers (multiplikatives Gesetz).
H ' = M ('; #) H 1'
(11)
Z12 beschreibt die Kopplung der zweiten Antenne zur ersten und kann für variablen Abstand d der Stäbe
aus folgender Ortskurve entnommen werden:
In der Horizontalen ergibt sich durch Überlagerung der Ausdruck:
I
M ' = 1 + 2 e j'x
I1
'x
= k0 r
mit
r = d cos('):
TU Berlin – FG Hochfrequenztechnik
(12)
(13)
HFT-Praktikum I
Lineare Antennen
LA/7
Bild 10: Strahlungsgekoppelte Elemente.
Bild 11: Ortskurve für Z12 (Heilmann [2]) für h
TU Berlin – FG Hochfrequenztechnik
=4.
HFT-Praktikum I
Lineare Antennen
LA/8
Besonders hohe Werte der Fernfeldintensität ergeben sich an den Stellen, wo der rechte Ausdruck (I 1=I 2 : : : )
etwa phasenrichtig zu 1 addiert wird, der Term also nahezu reell wird. Von Direktor- oder Reflektorwirkung
spricht man dann, wenn die Abstrahlung in Richtung der Struktur unterstützt bzw. vermindert wird. Die
Diagrammform zeigt aber auch bei anderen Konfigurationen als dem erwähnten Sonderfall deutliche Vorzugsrichtung der Abstrahlung.
Nach Einsatz aller bisherigen Ausdrücke und unter Verwendung des Umkehrsatzes (Z 21
sich
I2
I1
und
M' = 1 +
j'
12 j e
= jjZ
Z 22 j e j'
12
(14)
22
jZ 12 j e j (+' +'
jI 22 j
x
= Z 12 ) [2] ergeben
12
'22 ) :
(15)
Die Änderung von '22 wird durch Variation der Länge des strahlungsgekoppelten Elements erreicht.
7. YAGI-Antenne
Mehrere in Reihe angebrachte Direktoren können sich in ihrer Wirkung verstärken. Die Hauptkeule einer
solchen YAGI-Antenne weist deshalb in Richtung kleiner werdender Elemente. Meist genügt ein Reflektor,
um die Abstrahlung in Rückwärtsrichtung zu unterbinden. Seine Wirkung kann hingegen durch weitere
Reflektoren erhöht werden, die abweichend von der Strukturrichtung in gleichem Abstand zum gespeisten
Element angebracht sind.
Bild 12: YAGI-Antenne – prinzipieller Aufbau (links) und Richtdiagramm (rechts).
Ziel ist es, einen möglichst hohen Gewinn an Leistungsdichte (S ) in Hauptstrahlrichtung zu erzielen, jeweils
in Bezug auf eine Referenzantenne ohne Direktoren. Dieser Gewinn ist folgendermaßen definiert:
Smax Pref
Smax G=
= S Sref PAnt
ref
Pr ef =PAnt
(16)
Pref ; PAnt sind jeweils die zugeführten Leistungen.
8. Definition des Reflexionsfaktors
Für die Messungen an den Antennen müssen die Zuleitungen so angepasst werden, dass keine Reflexionen am Antenneneingang entsteht. Dazu wird der Reflexionsfaktor gemessen und das Anpassnetzwerk am
Antenneneingang so lange variiert, bis der Reflexionsfaktor minimal wird.
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
Ab Frequenzen oberhalb etwa
ben. Er ist definiert als
LA/9
100 Mhz werden Eintore zweckmäßig durch den Reflexionsfaktor beschrier (z ) =
U r (z )
U h (z )
(17)
mit U r Spannung der rücklaufenden Welle, U h Spannung der hinlaufenden Welle sowie z Ortskoordinate
auf der Leitung und macht somit eine Aussage über das komplexe Spannungsverhältnis der vom Eintor
reflektierten und der hineinlaufenden Welle. Der Reflexionsfaktor charakterisiert also den Abschluss einer
Leitung vollständig und eindeutig. Mit Hilfe der Leitungsgleichungen kann der Reflexionsfaktor folgendermaßen dargestellt werden:
r (z ) =
Z (l )=ZL 1
e j 2z (l z )
Z (l )=ZL + 1
(18)
Bild 13: Schaltung zur Messung des Reflexionsfaktors r (z ).
Dabei wird dem Eintor die Impedanz Z (l ) zugeordnet und der Leitung der charakteristische Widerstand ZL .
Aus dieser Formulierung ergibt sich unmittelbar die Möglichkeit, den Reflexionsfaktor in Polarkoordinaten,
also nach Betrag und Phase, darzustellen. Der Betrag wird häufig als Rückflussdämpfung (engl. Return
Loss) angegeben mit
20 log jr j
RTL[dB ] =
(19)
Gl. (18) enthält die Äquivalenz von Reflexionsfaktor- und Widerstandsebene im Sinne der konformen Abbildung
r
L 1
= Z=Z
;
Z=Z + 1
L
(20)
aus welcher das bekannte Smith-Diagramm folgt. Mit seiner Hilfe ist es möglich, die Korrespondenz zwischen Reflektionsfaktor und auf ZL normiertem, komplexen Widerstand graphisch darzustellen. Einige Beispiele dafür sind Abb. 14 zu entnehmen.
Typische Fälle sind z.B.:
1. Z=ZL
= 1; r = 0 (Anpassung)
2. Z=ZL
= 0; r = 1 (idealer Kurzschluss)
3. Z=ZL
! 1; r = 1 (idealer Leerlauf)
4. Z=ZL
= 2; r = 0; 33 (Abschluss mit Z = 2ZL )
5. Z=ZL
= j; r = j (Abschluss mit Z = jZL )
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/10
Bild 14: Beispiele zur Darstellung des Refelxionsfaktors im Smith-Diagramm. Die Parameter für die Kurvenscharen im Diagramm gelten für konstante Werte von <(Z=ZL ) bzw. =(Z=ZL ).
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/11
9. Messung des Reflexionsfaktors
Zur Messung des Reflexionsfaktors gibt es je nach Problemstellung eine Vielzahl von Verfahren. Erwähnt
sei von diesen zunächst die Messleitung als klassische Methode, bei welcher die durch Interferenz hinund rücklaufender Wellen sich ergebende ortsfeste Feldverteilung (eine stehende Welle) in der Leitung
gemessen wird. Man erhält damit Betrag und Phase des Reflexionsfaktors, hat jedoch die Messung für
jede Frequenz erneut durchzuführen.
Zur einfachen Messung ganzer Frequenzbänder eignet sich gut die sog. Reflektometerschaltung. Hier wird
mit Richtkopplern eine Trennung zwischen hin- und rücklaufenden Wellen vorgenommen, so dass bei einer
entsprechenden Auswertung eine direkte Anzeige des Return Loss erfolgt.
Bild 15: Reflektometerschaltung
Diese Methode ist zur Wobbelung (bezeichnet das kontinuierliche Durchstimmen eines bestimmten Frequenzbereiches durch sägezahnförmige Ansteuerung des Generators) geeignet, gestattet jedoch in dieser
Form keine Phasenmessung, weil die Detektoren die Phase nicht auswerten. Die Wobbelmessung des Reflexionsfaktors, sowohl nach Betrag und Phase, erfordert einen erheblich größeren Aufwand. Es wird ein
Netzwerk-Analysator verwendet, der im folgenden Abschnitt beschrieben wird.
10. Netzwerk-Analysator (Network Analyser)
Abb. 16 zeigt den Aufbau zur Messung des Reflexionsfaktors. Er besteht aus einem im Bereich 4 : : : 1300 MHz
durchstimmbaren Generator (bzw. mit externem Frequenzverdoppler 8 : : : 2600 MHz) mit digitaler Frequenzanzeige, einem abgestimmten Empfänger mit zwei unabhängigen Messkanälen, sowie einem Bildschirm
mit Rechteck- und Polarkoordinatenraster.
Es ist leicht zu ersehen, dass der Messaufbau grundsätzlich der Reflektometerschaltung entspricht, die
im vorangegangenen Abschnitt beschrieben wurde. Gleichermaßen wird die vom Generator eingespeiste
hinlaufende Welle von der am Messobjekt reflektierten Welle durch eine Richtkopplereinheit (Test Set) in
eine Referenz- und eine Testgröße getrennt. Abweichend vom einfachen Messverfahren wird nun jedoch im
Empfänger mit einem Mischer eine phasenkohärente Umsetzung dieser Signale in eine ZwischenfrequenzEbene (ZF-Ebene) vorgenommen, in welcher dann die Auswertung und nachfolgend auf dem Schirm die
Anzeige des komplexen Reflexionsfaktors nach Betrag und Phase erfolgt. Wegen der phasenempfindlichen
Messung müssen die Laufzeiten des Referenz- und des Messsignals gleich sein,
lRef
= lT est + 2lz ;
TU Berlin – FG Hochfrequenztechnik
(21)
HFT-Praktikum I
Lineare Antennen
LA/12
Bild 16: Messaufbau mit Netzwerk-Analysator
d.h. die zusätzliche Zuleitungslänge muss kompensiert werden.
11. Messung der Richtdiagramme
Für die Messung der Richtdiagramme sind folgende Punkte zu berücksichtigen:
• Der Sender (2; 5 GHz) liefert ein mit
1 kHz amplitudenmoduliertes Signal. Die Messobjekte sind in
entsprechende Löcher der Grundplatte des Antennenmessplatzes zu stecken.
• Die Empfangssonden tasten das Feld auf kreisförmigen Bahnen horizontal und vertikal in ca.
50 cm
Entfernung von der Antenne ab.
• Durch die Signalverarbeitung im Lock-In-Verstärker erreicht man eine leistungsproportionale Anzeige
des Empfangssignals. Der selektive Verstärker für f
= 1 kHz (enthalten in einem SWR-Meter) soll
Rauscheinflüsse und Drifterscheinungen (infolge Temperaturschwankungen) mindern.
• Der Gewinn einer Antenne ergibt sich durch Vergleich der Messergebnisse mit denen einer Referenz-
antenne (z.B. =4-Monopol) bei gleicher zugeführter Leistung (siehe Gl. (16)). Da der Fußpunktwiderstand ZF der zu vergleichenden Antennen verschieden ist, würde die zugeführte Leistung antennenabhängig werden und müsste bei der Gewinnermittlung berücksichtigt werden. Deshalb wird hier
mit Hilfe einer Anpassschaltung ZF auf den Leitungswellenwiderstand ZL
= 50 am Eingang der An-
passschaltung transformiert und damit Unabhängigkeit der den Antennen zugeführten Leistung von
ZF erreicht, wenn die Verluste des Anpassschaltung konstant oder vernachlässigbar sind.
• Vor der Messung eines Richtdiagramms muss deshalb durch Veränderung der Längen der Stichleitung der Anpassschaltung die über einen Richtkoppler gemessene rücklaufende Leistung Pr minimal
werden, damit sichergestellt ist, dass Anpassung vorliegt.
Literatur
[1] Petermann: Vorlesung Hochfrequenztechnik
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
Bild 17: Versuchsaufbau
[2] Heilmann: Antennen I, II, III. B.I.-Hochschulstaschenbücher
[3] King: The Theory of Linear Antennas. Harvard Univ. Press, Cambridge, Mass., 1956
[4] Balanis: Antenna Theory: Analysis and Design. Wiley & Sons, 3. Aufl. 2005
[5] Zinke/Brunswig: Lehrbuch der Hochfrequenztechnik, Bd. 1. Springer-Verlag, 3.Aufl., 1986
[6] Unger: Elektromagnetische Theorie für die Hochfrequenztechnik I. Hüthig Verlag
TU Berlin – FG Hochfrequenztechnik
LA/13
HFT-Praktikum I
Lineare Antennen
LA/14
A. Aufgaben
A.1. Vorbereitung
1. Der Gruppenfaktor M (') einer Monopol-Direktor-Anordnung ist anhand gegebener Werte zu bestimmen. Für eine grobe Aussage sind drei Stützpunkte für ' ausreichend (z.B. ' = 0 ; 90 ; 180 ). Die im
Versuch benutzten Elemente haben folgende Abmessungen:
= 30 mm, 2a = 1; 5 mm, d = 15 mm (Höhe und Druchmesser)
Direktor: h = 27 mm, 2a = 1; 5 mm, d = 15 mm
Monopol: h
2. Z 12 und Z 22 sind den Diagrammen in Bild 11 und 18 zu entnehmen. Betriebsfrequenz ist 2,5GHz.
Welche Tendenz zeigt die Fußpunktimpedanz beim Vergeleich Monopol ohne/mit Direktor (h ist in der
Abbildung 18 die Höhe des Direktors)?
Bild 18: Z 22 -Ortskurve.
A.2. Messung
1. Arbeiten mit dem Netzwerkanalysator
a) Messen Sie die Fußpunktimpedanz und die Resonanzfrequenzen eines Monopols im Bereich
f
= 0 : : : 1; 3 GHz für folgende Fälle:
i. dünner Monopol (h = 125 mm, 2a = 1; 5 mm)
ii. dicker Monopol (h = 125 mm, 2a = 10 mm)
b) Messen Sie die Resonanzfrequenz des dünnen Monopols aus I) mit Dachkapazität.
Die Messungen sind auf einem X-Y-Schreiber zu dokumentieren.
2. Messen Sie die Vertikaldiagramme (Richtdiagramme) bei 2; 5 GHz für folgende Monopole:
TU Berlin – FG Hochfrequenztechnik
HFT-Praktikum I
Lineare Antennen
LA/15
= =12
h = =2
h = 3=4
a) h
b)
c)
3. Messen Sie die Horizontaldiagramme folgender Anordnung (d
= 15 mm):
a) Monopol (=4),
b) Monopol mit Direktor,
c) Monopol mit Reflektor,
d) Monopol mit Reflektor und Direktor.
A.3. Auswertung
1.
a) Vergleichen Sie für den dünnen und den dicken Monopol die gemessenen Resonanzfrequenzen
mit den theoretisch ermittelten Werten, und schätzen Sie den Wellenwiderstand der Antennen
ab!
b) Berechnen Sie die Größe der Dachkapazität.
2. Zeichnen Sie die Vertikaldiagramme.
3.
a) Zeichnen Sie die Horizontaldiagramme und bestimmen Sie die Halbwertsbreiten.
b) Welche Gewinne erhält man für die Yagi-Antennen (aus Messungen 3.) bezüglich des =4Monopols (3a)?
Die meisten Punkte der Auswertung können und sollten bereits während des Laborversuchs bearbeitet
werden.
TU Berlin – FG Hochfrequenztechnik