LÖSUNGSMUSTER A 1.0 Die nebenstehende Skizze zeigt ein

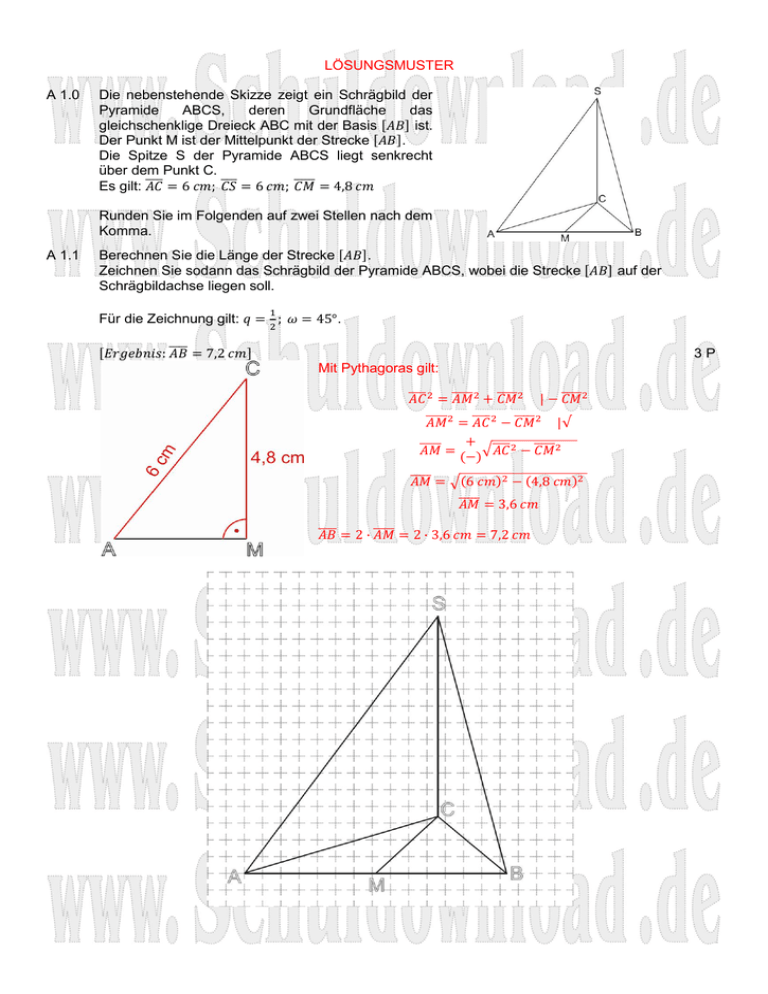
LÖSUNGSMUSTER
A 1.0
Die nebenstehende Skizze zeigt ein Schrägbild der
Pyramide
ABCS,
deren
Grundfläche
das
gleichschenklige Dreieck ABC mit der Basis
ist.
Der Punkt M ist der Mittelpunkt der Strecke
.
Die Spitze S der Pyramide ABCS liegt senkrecht
über dem Punkt C.
Es gilt:
Runden Sie im Folgenden auf zwei Stellen nach dem
Komma.
A 1.1
Berechnen Sie die Länge der Strecke
.
Zeichnen Sie sodann das Schrägbild der Pyramide ABCS, wobei die Strecke
Schrägbildachse liegen soll.
Für die Zeichnung gilt:
auf der
.
3P
Mit Pythagoras gilt:
A 1.2
Berechnen Sie die Länge der Strecke
und das Maß
Seitenfläche ABS gegen die Grundfläche ABC.
des Neigungswinkels der
2P
Bisher bekannte Größen werden in der
Skizze eingetragen:
Aus der Schrägbildskizze heraus erkennt
man, dass eine Skizze des Dreiecks MCS
ratsam ist:
Auf bezogen sind im rechtwinkligen Dreieck MCS
Gegenkathete und Kathete bekannt. Daher bietet sich das
Arbeiten mit dem Tangens an:
erhalten wir am leichtesten mit der Formel des Pythagoras:
A 1.3
Für den Punkt F gilt:
und
. Der Winkel
sei der Neigungswinkel der
Strecke
gegen die Grundfläche der Pyramide
Zeichnen Sie den Punkt F in das Schrägbild zu 1.1 ein und ermitteln Sie sodann das Maß
des Winkels durch Rechnung.
Skizze:
Die gesuchte Größe befindet
sich im Dreieck MSC, es bietet
sich eine Skizze dieses
Dreiecks an:
Das Maß des Winkels
beträgt:
Mit dem Kosinussatz ergibt sich folgender Zusammenhang:
bzw.:
Damit gilt mit dem Sinussatz im Dreieck CMF:
4P
A 1.4
Punkte
und Punkte
sind zusammen mit den Punkten A und B die
Eckpunkte von Trapezen
. Die Mittelpunkte der Strecken
sind die Punkte .
Es gilt:
und
(
).
Zeichnen Sie für
das Trapez
in das Schrägbild zu 1.1 ein.
Berechnen Sie sodann die Länge der Strecken
in Abhängigkeit von x.
3P
Das Trapez
wird in die
Skizze übertragen, in der alle
bereits berechneten Größen
notiert sind:
Um die Länge der Strecke
in Abhängigkeit von x zu
berechnen, zeichnen wir das
relevante Dreieck ABC.
Mit dem Vierstreckensatz gilt:
A 1.5
Die Trapeze
sind die Grundflächen von Pyramiden
mit der Spitze F.
Zeichnen Sie die Pyramide
und ihre Höhe
mit dem Höhenfußpunkt
in das Schrägbild zu 1.1 ein.
Zeigen Sie durch Rechnung, dass sich das Volumen V der Pyramiden
Abhängigkeit von x wie folgt darstellen lässt:
in
3P
Das Volumen der Pyramide
lässt sich mit der folgenden
Formel berechnen:
Berechnung der Grundfläche:
Nun ermitteln wir die Höhe
.
Hierfür betrachten wir die Skizze, in
der alle bekannten Größen
eingetragen sind:
Das Dreieck MHF enthält die gesuchte Strecke
Mit dem Sinus gilt:
A 1.6
Das Volumen der Pyramide
beträgt 20% des Volumens der Pyramide ABCS.
Berechnen Sie den zugehörigen Wert von x.
Zunächst muss das Volumen der Pyramide ABCS mit der Formel
berechnet werden. Für den Flächeninhalt der Grundfläche
gilt:
Damit gilt für das Volumen der Pyramide ABCS:
Die Pyramide
soll 20% dieses Volumens haben:
Einen Zusammenhang zwischen Volumen und dem jeweiligen x finden wir mit:
eingesetzt:
Mit der Mitternachtsformel gilt:
liegt nicht in der Definitionsmenge von x (siehe Angabe!)
3P
B 1.0
Die nebenstehende Skizze zeigt den Plan eines
trapezförmigen
Gartengrundstücks
mit
einer
kreissektorförmigen Terrasse. Es gelten folgende Maße:
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
B 1.1
Berechnen Sie den Flächeninhalt A der Terrasse.
2P
B 1.2
Im Plan zeigt der Punkt G die Lage einer Steckdose, zu der vom Punkt E aus eine geradlinig
verlegte Stromleitung führt. Berechnen Sie die Länge der Strecke
.
Berechnung mit dem Kosinussatz:
2P
bzw.:
B 2.1
Ordne die folgenden Funktionsgleichungen den passenden Schaubildern zu.
(Notiere jeweils unter einen Graphen die passende Nummer.)
5P
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
4.
2.
8.
3.
1.
5.
10.
6.
9.
7.