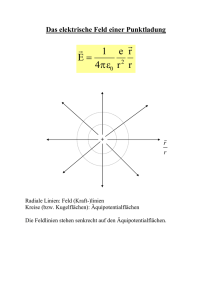
Lösung - extremstark.de

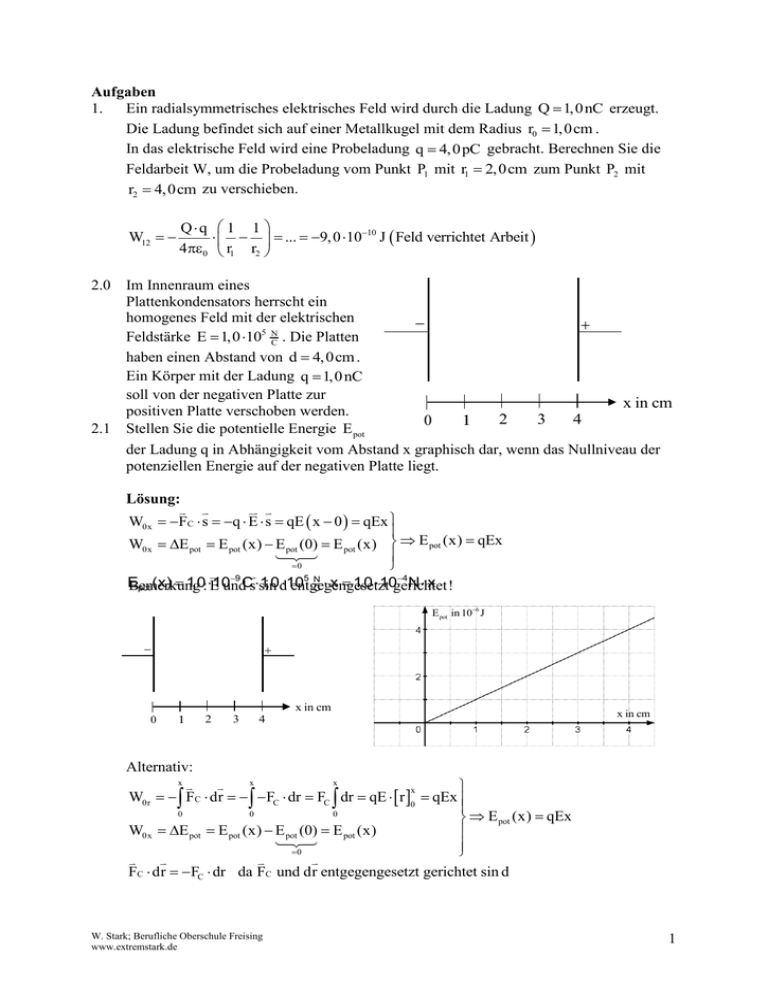
Aufgaben
1.
Ein radialsymmetrisches elektrisches Feld wird durch die Ladung Q  1,0 nC erzeugt.
Die Ladung befindet sich auf einer Metallkugel mit dem Radius r0  1,0cm .
In das elektrische Feld wird eine Probeladung q  4,0 pC gebracht. Berechnen Sie die
Feldarbeit W, um die Probeladung vom Punkt P1 mit r1  2,0cm zum Punkt P2 mit
r2  4,0cm zu verschieben.
W12  
2.0
2.1
Qq  1 1 
     ...  9, 0 1010 J  Feld verrichtet Arbeit 
40  r1 r2 
Im Innenraum eines
Plattenkondensators herrscht ein
homogenes Feld mit der elektrischen


Feldstärke E  1,0 105 NC . Die Platten
haben einen Abstand von d  4,0cm .
Ein Körper mit der Ladung q  1,0 nC
soll von der negativen Platte zur
x in cm
positiven Platte verschoben werden.
3
2
4
0
1
Stellen Sie die potentielle Energie E pot
der Ladung q in Abhängigkeit vom Abstand x graphisch dar, wenn das Nullniveau der
potenziellen Energie auf der negativen Platte liegt.
Lösung:
W0x  FC  s  q  E  s  qE  x  0   qEx 

W0x  E pot  E pot (x)  E pot (0)  E pot (x)   E pot (x)  qEx

0

9
5 N
4
E
10undCssin
1,0d 10
 x  1,0  10gerichtet!
N x
Bemerkung
entgegengesetzt
pot (x)  1,0: E
C
E pot in 106 J


x in cm
0
1
2
3
4
x in cm
Alternativ:
x
x
x

x
W0r    FC  dr    FC  dr  FC  dr  qE   r 0  qEx 

0
0
0
  E pot (x)  qEx
W0x  E pot  E pot (x)  E pot (0)  E pot (x)


0
FC  dr  FC  dr da FC und dr entgegengesetzt gerichtet sin d
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
1
2.2
Der Körper mit der Ladung q wird bei x  d aus dem Ruhezustand freigegeben.
Berechnen Sie die Auftreffgeschwindigkeit v E auf der negativ geladenen
Kondensatorplatte und die Flugdauer t F des Körpers, wenn dieser die Masse
m  2,0 g hat.
Lösung: Es gilt für die Beschleunigungsarbeit Wa
1
2
Wa  W0x  E pot (x)
mv 2E  qEx
vE 
2qEx
m
2 1, 0 109 C 1, 0 105 NC  4, 0 102 m
vE 
 63 ms
9
2, 0 10 kg
Die beschleunigende Kraft Fa auf die Ladung q ist die Coulombkraft FC . Es gilt:
Fa  FC
ma  qE
a
qE
m
Es gilt: vE  at F  t F 
3.0
3.1
2, 0 109 kg  63,3 ms
vE mvE


 1,3 103 s
a
qE 1, 0 109 C 1, 0 105 NC
Nach der Bohr’schen Theorie für das Wasserstoffatom kann das Elektron den Atomkern
(Proton) nur auf bestimmten Kreisbahnen, den so genannten Quantenbahnen, umlaufen.
Die kleinste Kreisbahn des Elektrons (1. Quantenbahn) hat den Radius r1  5,3 1011 m
Berechnen Sie die Geschwindigkeit v1 des Elektrons auf der 1. Quantenbahn.
F Z  FC
m
v12
1 e2


r1 40 r12

m  v12 
1 e2

40 r1

E kin  12  m  v12 
1 e2

80 r1
1, 602 1019 C 

e2
v1 

 2, 2 106
As
40  m  r1
4  8,854 1012 Vm
 9,109 1031 kg  5,3 1011 m
2
3.2
m
s
Berechnen Sie die Gesamtenergie E Ges des Elektrons auf der 1. Quantenbahn
Hinweis: Das Nullniveau der potentiellen Energie soll im Unendlichen liegen.
 1 1 Qq 1 
1
Qq   
 
Qq 1
40
 r r  4 0 r 

  E pot (r) 
40 r
Wr  E pot  E pot (r)  E pot (r )  E pot (r) 

0

e  e 1
e2 1
e2
E Ges  r1   E pot  r1   E kin  r1  
 
 
40 r1 80 r1
80  r1
Wr  
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
2
E Ges  
E Ges  
3.3
1, 602 10
8 8,854 1012
As
Vm
C
2
 5,3 1011 m
 2,18 1018 J
1, 602 1019 C  e
 13, 6eV
As
8 8,854 1012 Vm
 5,3 1011 m
Berechnen Sie die Energiedifferenz E , um das Elektron von der 1. Quantenbahn ins
Unendliche zu bringen.
Welche Bedeutung hat dieser Energiebetrag für das Wasserstoffatom?
E  EGes
3.4
19
Ionisierungsenergie
Berechnen Sie, welche Arbeit verrichtet werden muss, um das Elektron von der
Umlaufbahn r1 in die nächste Umlaufbahn (2. Quantenbahn) r2  2,11010 m zu
bringen.
W  E  E Ges  r2   E Ges  r1   
W
W
1, 602 10
19
8  8,854 10
C
2
12 As
Vm

e2
e2 
e2  1 1 



  
80  r2  80  r2  80  r1 r2 


1
1
18


  1, 6 10 J
11
10
 5,3 10 m 2,1 10 m 

1, 602 1019 C  e 
1
1


  10,1eV
12 As 
11
10
8  8,854 10 Vm  5,3 10 m 2,1 10 m 
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
3