Grundbegriffe und Coulombsches Gesetz

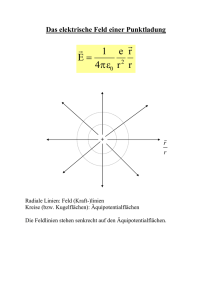
1. Elektrostatik (Kräfte zur ruhenden Ladung)
lap5/adm/Eig/LATEX/Vorl/PhysII/Scriptum/Kap1_1/kap1_1_a4.tex
1.1 Grundbegriffe u. Coulombsches Gesetz
Vorbereitende Bemerkungen:
⃗) wurde untersucht;
In Mechanik: Verhalten von Körper unter Kräften (F
nächster Schritt: Ursache der Kräfte ?
Körper aus Molekülen-Atomen-Kern+Hülle - Nukleonen-Quarks ...aufgebaut
Grundsätzliche Fragen:
Baustein der Materie?
Kräfte zwischen den Bausteinen?
Schon kennengelernt: Gravitation! Quelle und Objekt ist hier die Masse
Grav. wirkt durch den Raum: d.h. m 1 in ⃗r 1 hat Einfluß auf m 2 in ⃗r 2 : Raum in ⃗r 2 durch m 1
verändert (Feld) ’leerer Raum’ kann Fernwirkung schwer übermitteln. (Feld=von Kraftwirkung
erfüllter Raum)
moderne Ansicht: Feldquanten übermitteln Wirkung
⇒
Bisher bekannte Kräfte:
∙
Gravitation
∙
Elektr.-schwache WW.
Quelle/Obj.
Feldquant
Masse
Gravitation (hypothet.)
(=elektr + magn. +schw.)
elmag. Anteil
∙
schwacher Anteil
(radioakt. Zerfall )
∙
Q el. Ladung Photon
schwache L.
Z o , W+ , W−
Farbladung
Gluon (8 versch.)
Starke WW
Kernkräfte
Grundbegriffe:
Zur elektr. Ladung Q:
im Gegensatz zur Masse: Q kommt frei nur als ganzzahliges Vielfaches einer Elementarladung
vor
∙ 2 Werte möglich: +/-, kompensieren sich gegenseitig.
∙ Bewegte Ladung = Strom:
Neben elektrostatischen Kräfte treten bei bewegten Ladungen (= Ströme) magnetische Kräfte auf.
I = Qt
I...über Kraft-Wirkung def: Einheit des Stromes, 1 Ampere, lliegt dann vor, wenn
sich 2 von diesem Strom durchflossene Leiter (pro Meter) in einem m Abstand voneinander mit
einer Kraft von 2.10 −7 N/m anziehen (später genauer).
Kohärent definierte Einheit der Ladung daher: [Q]=1.A.1.s = 1 Coulomb, die Elementarladung
beträgt e = 1, 6.10 −19 C
∙ In einem abgeschlossenem System gilt für Q ges ein Erhaltungssatz .
∙
⇒
Coulomb’sches Gesetz:
F zwischen Q : empirisches Resultat: Ganz analog zum Gravitationsgesetz. Ladung als Quelle des
elmag. Feldes (d.h. als Ursache der Kraftwirkung auf andere Ladung) tritt an Stelle der Massen,
Kraft nimmt wieder mit r12 ab.
Für punktförmige Ladungen daher:
F = const.
Q1Q2
r2
⃗ = const.
F
Q1Q2 ⃗
Q Q
e r = const. 1 3 2 ⃗r
r2
r
Diese Gleichung beschreibt also die Kraft F von Q 1 auf Q 2 , für die Konstante wird die Form
1
const = 4πε
gewählt, damit ergibt sich nämlich im Nenner der Ausdruck 4πr 2 , der besonders
0
für Betrachtungen in Polarkoordinaten sehr vorteilhaft ist. Der Wert der Größe ε 0 (”Feldkonstante,
Influenzkonstante”) ist dann experimentell zu bestimmen und beträgt
c
ε 0 = 8, 85.10 −12 [ Vm
]., die Dimension im SI-System ist dann:
2
Q
q
Q
A 2 sec 4
C
[ε 0 ] = [ Fr 2 ] =
= F[Q]
= [ E.r.r
= [ U.r
] = Vm
3
.r.r
kg m
Q
1 Q1Q2
4πε 0 r 2
F auf Q 2 durch Q 1 wirkt entlang der Verbindungsgeraden zwischen den beiden Ladungen:
’Zentralkraft’.
Wenn versch. Vorzeichen, abstoßend, , wenn gleiche Vorzeichen: anziehend.
F=
1.2 Elektrische . Feldstärke u. Potentialdifferenz, Spannung:
andere Betrachtungsweise:
in Raum (Feld = von Kraftwirkung erfüllter Raum). Maß für Wirkung des Feldes: Kraft auf
Ladung Q 2 .
Q 2 spürt das von Q 1 erzeugte Feld.
⃗ eingeführt:
Es wird der Begriff der Feldstärke E
∙
⃗
F
⃗
(r⃗) =: E
Q2
∗)
⃗=E
⃗ ⋅ Q2
F
1 Q
4πε 0 r 2
als f(r⃗) el. Eigenschaft des Raumes, wenn Q 1 sich in ⃗r = 0 befindet
E=
beschreibt
⃗
F
Q2
⃗ ∥ ⃗r, daher wegen *) auch E
⃗ ∥ ⃗r
Es war: Richtung von F
⃗
E wirkt In Richtung des Punktes ⃗r = 0, also auf die Quellenladung zu (Anziehung), wenn
( ∣QQ 11 ∣ + ∣QQ 22 ∣ = 0) d.h für entgegengesetztes Vorzeichen, bei gleichen Vorzeichen der beiden
Ladungen erfolgt Abstoßung
⃗ hat Betrag und Richtung wie die Kraft F, die auf eine positive Einheitsladung wirkt.
E
∙ Veranschaulichung von E: durch Feldlinien:
⃗ : Ist ein ortsabhänginger Vektor: daher wäre für jeden Punkt im
Probleme bei der Darstellung von E
Raum die Angabe von drei Größen erforderlich.
Alternative: Feldlinien!
⃗ hat Richtung der Tangente an die Feldlinien.
a) Lassen Richtung der F im Raum erkennen: F
Kugelsym. Feld einer ruhenden Punktladung: Stärke hängt von Stärke der Ladung Q ab;
⇒
b) Stärke des Feldes durch Dichte der Linien gekennzeichnet.
r2
E(r )
N
1
⃗ | ∼ N z.B. E 1 = N
|E
E 2 ∼ 4πr
, E(r 12 ) = N/A
= r 22
2
N/A 2
A
4πr 2
1
2
1
Potential
⃗ (r⃗) durch eine
Einführung der Größe des Potentials V(r⃗) ermöglicht Darstellung des Vektors E
skalare Größe.
⃗ wichtige, anschauliche, aber unhandliche Größe, da Vektor (3 Komp.)
Idee wie zuvor: E
⃗ und potentieller Energie W pot veranschaulicht:
Ausweg über Potential: an F
Wird zu jedem Punkt im Raum die potentielle Energie W pot (r⃗) angegeben, dann ist Änderung der
⃗:
skalaren Größe W pot ein Maß für die wirkende Kraft F
⃗
z.B. für F = const :
△W pot
⃗r
= −F
⋅ △⃗
r
= −F ⋅ △r ⋅ ⃗e F ⋅ ⃗e r
= −F ⋅ △r ⋅ cos α
cosα
Für α = π, also cos α = −1 ist daher △W pot = F ⋅ △r, beschreibt also die Zunahme der
potentiellen Energie, wenn ein Weg gegen eine wirkende Kraft zurückgelgt wird. Ist bei
gegebenem Weg △r diese Zunahme groß, so bedeutet das, daß die Kraftkomponente in Richtung
dieses Weges groß sein muß. Diese Überlegung gilt für jede Richtung, also auch für jede
Komponente:
⃗ r ⋅ △⃗r = −F x △x − F y △y − F z △z = − F x △x i daher ist also auch F x = − △Wpot ,
△W pot = −F
i
i
△x i
⃗
⃗
⃗
Ist die Kraft F ortsabhängig: F = F(r), dann gilt analog für ein infinitesimales Wegelement dr⃗:
⃗ ⋅ dr⃗ = −F ⋅ ⃗e F ⋅ dr ⋅ ⃗e r = −F ⋅ dr ⋅ ⃗e F ⃗e r = −F ⋅ dr ⋅ cos α
dW pot = −F
Und wieder gilt z.B. bei ⃗e F ⃗e r = cos α = −1,: dW pot = F ⋅ dr, ist die Kraft dem gewählten Weg
entgegengerichtet,
ist die Änderung der potentiellen Energie dW pot also positiv (W pot nimmt dabei zu)
∑
Elektrisches Feld einer Punktladung:
⃗ = Q 1 Q 2 ⃗e r .. Kraft von Q 1 , die sich in in ⃗r = 0 befindet, auf Q 2 (r⃗)
F
4πε 0 r 2
wenn, Q 1 > 0, Q 2 > 0: F in Richtung von ⃗e r , also.abstoßend!
Da Feld der Punktladung richtungsabhängig ist (radialsym. Anordnung, unabhängig vom
gewählten ⃗e r ):
Q1Q2
= rC2
F r = F(r) = 4πε
2
0r
∙ Verschieben von Q 2 um △⃗
r = ⃗r 2 − ⃗r 1 , △r = r 2 − r 1 : dW pot = −Fdr
r
2
Q1Q2
mit c = 4πε 0 ist dann △W pot = − r 2 F(r)dr = −c 1 r12 dr =
1
= −c(− 1r ∣ 21 = cr ∣ 21 = c( r12 − r11 )
1Q2 1
z.B. r 1 = ∞, r 2 = r : △W pot = cr = Q4πε
0 r
Probe:
dW
1Q2 1
F (r) = − drpot = −c drd ( 1r ) = −c(− r12 ) = rc2 = Q4πε
0 r2
∫
∫
⃗(r) = F(r)e⃗r kann aus den skalaren Feld W(r⃗) ausgerechnet werden!
Vektor F
⃗(r⃗) dr⃗ : dV = −E
⃗ (r) dr⃗ .. ∆V (= U)...Potentialdiffferenz zwischen
Üblich: Analog zu dW pot = −F
zwei Punkten, ”Spannung”. Dann ist also dW pot = Q ⋅ dV
⃗dr⃗ durch ∣ ⋅ 1
aus dW pot = −F
Q
dWp
Q
⇒E
⃗
= dV = − QF
r
=−
dV(r⃗)
dr
⋅ dr⃗ = −E⃗ ⋅ dr⃗ = −E ⋅ dr ⋅ cos α = E r ⋅ dr
gilt für jede Richtung:
∂V(r⃗)
∂x i
Da das Feld einer Punktldung radialsymmetrisch ist, rechnet man in diesem Fall am besten in
Polarkoordinaten, E hat dann nur eine radiale Komponente.
[Allgemein gilt also:
E x = − ∂V , E y = − ∂V , E z = − ∂V
∂x
∂y
∂z
⃗ = −( ∂V ⃗e x + ∂V ⃗e y + ∂V ⃗e z )
E
∂x
∂y
∂z
E xi = −
(Zeichen der partiellen Ableitung ∂ gibt an, daß V(x,y,z) jeweils nur nach einer dieser Variablen
abgeleitet wird.)
Formal:
⃗ = E x⃗e x + E y⃗e y + E z⃗e z = − ∂V ⃗e x − ∂V ⃗e y − ∂V ⃗e z ...
E
∂x
∂y
∂z
kann geschrieben werden als:”Gradient von V”
⃗ = −∇
⃗ V(r⃗)
E
⃗ ” einführt, der z.B. in kartesischen Kooerdinaten folgende
wenn man den Vektor-Operator ” ∇
Gestalt hat:
⃗ := ∂ ⃗e x + ∂ ⃗e y + ∂ ⃗e z
∇
∂x
∂y
∂z
⃗ ”NABLA-Operator”; Differentialoperator, (Nabla: Griechisches Saiteninstrument)]
∇