Alles relativ?

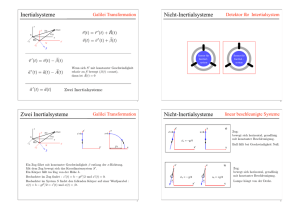
Physikwoche für Schüler
H.-J. Kull
RWTH Aachen
http://llp.ilt.fhg.de/vorlesungen.htm
Licht und
Relativität
Licht in bewegten
Bezugssystemen
Bewegte Bezugssysteme
S
S′
v
Das Satellitenlabor S′ bewegt sich relativ zu einem Labor
S auf der Erde mit der Geschwindigkeit v . Gelten in
S und S′dieselben physikalischen Gesetze?
Inertialsysteme
Sir Isaac Newton
1643-1727
• Es gibt bevorzugte
Bezugssysteme, in denen
sich ein kräftefreier
Körper geradlinig und mit
konstanter
Geschwindigkeit bewegt.
(1. Axiom von
Newton,1687)
• Solche
Bezugssysteme
heissen
Inertialsysteme
(z.B. Fixsternhimmel)
• Andere
Bezugssysteme sind
beschleunigt
(z.B. Karussell)
Galileisches Relativitätsprinzip
•
Ein Bezugssystem, das sich
relativ zu einem Inertialsystem
gleichförmig bewegt, ist selbst
ein Inertialsystem. Auch
räumlich gedrehte und
verschobene Inertialsysteme
sind selbst wieder
Inertialsysteme.
•
Für diese Systeme gilt das
nach Galilei benannte
Relativitätsprinzip:
Galileo Galilei, 1564-1642
Alle Inertialsysteme sind gleichwertig
Galileitransformation
• Ein Ereignis findet
im ruhenden System
S am Ort x zur Zeit t
statt, im bewegten
System S‘ am Ort x‘
zur Zeit t‘.
• Koordinatentransformation:
x′ = x − vt , t′ = t
S′
S
t
t′
x′
vt
x
t = t′
Geschwindigkeitsaddition
S
•
Geschwindigkeit in S:
•
Geschwindigkeit in S‘:
•
Die Geschwindigkeit im
bewegten System ist die
Relativgeschwindigkeit der
beiden Fahrer
u = x/t
u′ = x′ / t
x′ = x − vt
u′ = u − v
u = u′ + v
S′
x′ = u′t
x = vt
x = ut
Schallausbreitung
• Im Ruhesystem des
Mediums (z.B. Luft) ist
die Schallgeschwindigkeit
s unabhängig von der
Ausbreitungsrichtung.
• In einem bewegten
System ist die Schallgeschwindigkeit von der
Ausbreitungsrichtung
abhängig.
• Bewegung relativ zum
Medium ist nachweisbar!
st
vt
(s+v)t
(s-v)t
Lichtausbreitung
• Ätherhypothese: Licht
breitet sich wie Schall
in einem Medium,
dem Lichtäther, aus.
• Michelson-Morley
Experiment:
Eine Bewegung relativ
zum Lichtäther ist
nicht nachweisbar!
Michelson-Interferometer
v
Einsteinsches Relativitätsprinzip
y
• Alle
Inertialsysteme
sind
gleichberechtigt
• Licht breitet sich
in jedem
Inertialsystem
mit derselben
Geschwindigkeit
c aus
ct
x
vt
y′
ct′
x′
Lorentztransformation
(siehe Anhang A1)
x′ = γ ( x − vt )
t ′ = γ (t − vx / c )
2
γ =
1
1−
v2
c2
• Koordinatentransformation in ein mit der
Geschwindigkeit v bewegtes Inertialsystem
• Maßstabsänderung
• Invarianz der Lichtgeschwindigkeit
• Ort und Zeit transformieren sich gemeinsam
Längenkontraktion
• Ein bewegter
Maßstab erscheint
verkürzt
x' = γ ( x − vt )
Laborsystem S:
Ruhesystem S’:
x=L
x' = L0
t=0
L0 = γ L = L / 1 − v 2 / c 2
L = 1 − v 2 / c 2 L0
Garagenproblem
•
Ruhesystem der Garage
Gleichzeitigkeit ist
bezugssystemabhängig
G
A
ct
Bewegtes Auto paßt in ruhende
Garage
•
•
G
Ruhesystem des Autos
x
A
G
A
Ruhendes Auto paßt nicht in
bewegte Garage
Fensterproblem
•
Stab länger als Fensterhöhe
S
•
•
Passierbarkeit ist
bezugssystemunabhängig
!
F
F
Kann bewegter Stab Fenster
passieren?
v
S
?
F
S
Länge quer zur
Bewegungsrichtung bleibt
invariant
Zeitdehnung
• Eine bewegte Uhr
geht verlangsamt
v
t ' = γ (t − v/c 2 x)
Laborsystem S
x = vt
Ruhesystem S’
x' = 0
t' = 1 − v2 / c2 t
Zwillingsparadoxon
•
Momentane Zeitänderung
v2
dt ' = 1 − 2 dt
c
•
Gesamte Zeitänderung
50 Jahre
T
T'=
∫
t =0
2
v(t )
1− 2 dt
c
5 Minuten
v
Laufzeiteffekte
•
Bewegter Punkt wird an einem
früheren Ort wahrgenommen
x
ct
vt
x
•
Maßstäbe parallel und
senkrecht zur
Bewegungsrichtung
Dopplereffekt
• Invarianz der Phase einer Lichtwelle
φ = kx −ωt = γ [k(x′ + vt′) −ω(t′ + vx′ / c )]
2
= k′x′ −ω′t′ = φ′
• Lorentztransformation der Frequenz und
Wellenzahl
ω′ = γ (ω − kv)
• Rotverschiebung:
• Blauverschiebung:
2
′
k = γ (k − vω / c )
k ↑↑ v
k ↑↓ v
Beobachtung bewegter Körper
• Ein entfernter
bewegter Körper
erscheint gedreht
k x' = γ (k x − vω/c 2 )
k y' = k y
x
tan α =
ct
y
α
vt
ky = ω / c
kx = 0
cos α =
− k y'
k x'
v
c
1 − v2 / c2
=
v/c
Relativistische Elektronen
erzeugen Laserfelder
• Prinzip des freien Elektronenlasers
Laserstrahl
Elektronenstrahl
Periodische Struktur (Wiggler)
• Wigglerwellenläge im
Ruhesystem des Elektrons: λ′ = λ / γ
• Lichtfrequenz
′ = ck′ = γ 2πc / λ
ω
im Ruhesystem
v
2
• Lichtfrequenz
′
′
′
′
(
v
) = γ (1+ )2πc / λ
ω
=
γ
ω
+
k
im Laborsystem
c
Additionstheorem der Geschwindigkeiten
•
•
•
•
•
S‘ bewegt sich mit Geschwindigkeit u in S
Geschwindigkeit in S: v = x / t
v' = x ' / t '
Geschwindigkeit in S‘:
Lorentztransformation: x′ = γ ( x − vt )
Geschwindigkeitstransformation:
2
′
t = γ (t − vx / c )
v−u
x'
x − ut
=
v' = =
2
1 − uv / c 2
t ' t − ux / c
•
•
Umkehrung: S bewegt sich mit Geschwindigkeit –u in S‘
Beispiele:
4
c
5
c+u
v' = c, u < c : ⇒ v =
=c
1+ u / c
v' = c / 2, u = c / 2 : ⇒ v =
v'+u
v=
1 + uv' / c 2
Relativistische Mechanik
m( v ) = m0γ ( v) = m0 / 1 − v 2 / c 2
•
Nichtrelativistisch
•
p = m0 v
dx
v=
dt
•
Konstante Kraft
Widerspruch zum
Additionstheorem der
Geschwindigkeiten
dx
dt → dτ
dτ
dx dt
dx
p = m0
= m0
= m0 vγ = m( v ) v
dt dτ
dτ
p = m0u
•
dp
p = Ft
=F
dt
v
Ft
=
→∞
c m 0c
•
Relativistisch
u=
Konstante Kraft
dp
p = Ft
=F
dt
v
Ft / m0c
=
→1
2
c
1 + ( Ft / m0c )
•
Masse und Impuls beliebig
groß, Geschwindigkeit bleibt
beschränkt
Relativistische Energie
E = m( v )c 2 = m0γ ( v)c2 = m0c 2 / 1 − v 2 / c 2
•
Energieänderung durch Arbeit
dx
= v,
dt
•
dp
=F
dt
E = m0c 2 1 + ( p / m0c ) 2
dx
dp
p dp
1 dp 2
dE
=F
=v
=
=
dt
dt m0γ dt 2m0γ dt
dt
•
p = m γ v , q = v /c
2
2
0
2
2
2
p2
1
E ≈ m0c +
= m0c 2 + m0 v 2
2m0
2
2
p
= −1 + γ 2
2 2
m0 c
Ruheenergie + Kinetische Energie
•
Grenzfall:
2
p2
q
q −1+1
1
=
=
= −1 +
2 2
m0 c
1− q
1− q
1− q
p << m0c
2
E = m0γc 2 = m( v )c 2
Nebenrechnung
Grenzfall:
1 + ( p / m0c ) 2 ≈ (1 + 12 ( p / m0c ) 2 ) 2
m0c 2 dγ 2 d ( m0c 2γ )
=
=
2γ dt
dt
•
Energie-Impuls-Beziehung
p >> m0c
1 + ( p / m0c ) 2 ≈ ( p / m0c ) 2
E ≈ pc
z.B. Photon
Laserfelder erzeugen relativistische
Elektronen
• Relativistische
Simulation von
Atomclustern
in starken
Laserfeldern
I = 10 17 W/cm2
A1: Lorentztransformation
Ansatz mit Maßstabsfaktor
S′
S
x′
vt
x
x′ = γ ( x − vt )
• Transformation mit Maßstabsfaktor γ
• Richtungsunabhängigkeit: γ hängt vom Betrag
aber nicht von der Richtung der Geschwindigkeit
ab.
A1: Lorentztransformation
Umkehrtransformation
S′
S
−v
x = γ ( x′ − (− v)t ′)
x = γ ( x′ + vt ′)
• Für einen Beobachter in S′ bewegt sich S mit
der Geschwindigkeit − v
• Die Inertialsysteme sind gleichberechtigt:
x ↔ x′, t ↔ t ′ ⇔ v → − v
A1: Lorentztransformation
Invarianz der Lichtgeschwindigkeit
x = ct ⇔ x′ = ct′
Transformation
x′ = γ ( x − vt ) ⇒ ct ′ = γ (ct − vt ) = γ (1 − vc )ct
Umkehrtransformation
x = γ ( x′ + vt ′) ⇒ ct = γ (ct ′ + vt ′) = γ (1 + vc )ct ′
Bestimmung von
γ
1 = γ (1 − vc )γ (1 + vc ) = γ 2 (1 −
2
v
c2
)
γ =
1
1−
v2
c2
A1: Lorentztransformation
Zeittransformation
t ′ = γ (t − vx / c )
2
• Auflösen nach t‘:
x = γ ( x′ + vt ′) ⇒ γ vt ′ = x − γ x′
• Einsetzen von x‘:
2
2
x′ = γ ( x − vt ) ⇒ γ vt ′ = (1 − γ ) x + γ vt
• Einsetzen von γ :
2
v
1 − γ 2 = − 2 γ 2 ⇒ γ vt ′ = γ 2 v(t − vx / c 2 )
c
A2: Ereignisraum
Galileitransformation
t vt
t′ = 2
t′
P
x′
t′ = 0
x
t ′ = −2
x′ = −5
P : x = 0, x′ = −1
x′ = x − vt = a
x′ = 0
x′ = 5
⇔
x = vt + a
• Die Koodinatenlinien x′ = a aus S ′ werden in
auf die Geraden x = a + vt abgebildet.
• Abstände bleiben erhalten: ∆x′ = ∆x
S
A2: Ereignisraum
Lorentztransformation
b
t′ = b
γ
t′ = 0
x′ = 0
123
t ′ = γ (t − vx / c 2 ) = b
vx b
⇔ t= 2 +
c
γ
t
123 x
a
γ
x′ = a
x′ = γ ( x − vt ) = a ⇔
x = vt +
a
γ
A2: Ereignisraum
Längenkontraktion
Ein bewegter Stab
erscheint verkürzt
a
• Länge des in S‘
ruhenden Stabes: a
• Länge des in S
bewegten Stabes zur
Zeit t=0:
∆x =
a
γ
= 1 − v2 / c2 a
va
− 2
c
a
γ
A2: Ereignisraum
Zeitdehnung
Eine bewegte Uhr geht
verlangsamt
b
γ
• Zeitintervall der in S‘
ruhenden Uhr: b
• Zeitintervall der in S‘
bewegten Uhr:
b
∆t = = 1 − v 2 / c 2 b
γ
− vb
b