6. Mechanik deformierbarer Körper

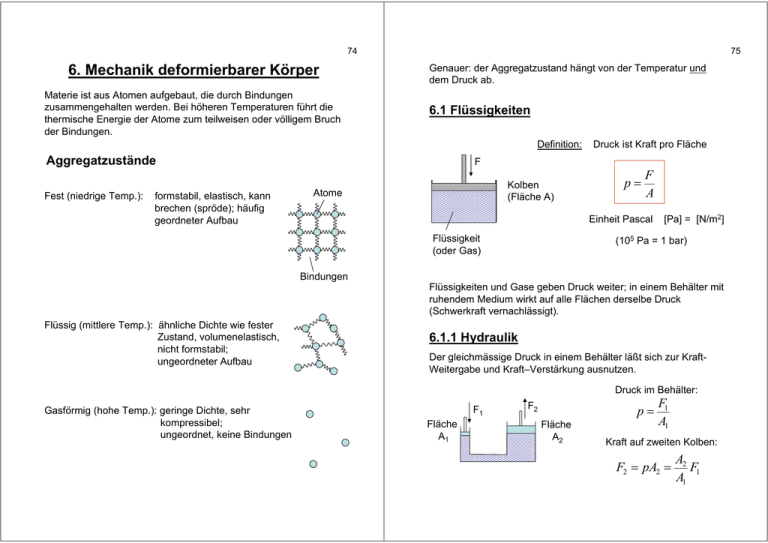
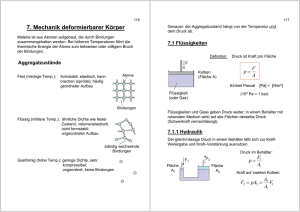
74
6. Mechanik deformierbarer Körper
Materie ist aus Atomen aufgebaut, die durch Bindungen
zusammengehalten werden. Bei höheren Temperaturen führt die
thermische Energie der Atome zum teilweisen oder völligem Bruch
der Bindungen.
75
Genauer: der Aggregatzustand hängt von der Temperatur und
dem Druck ab.
6.1 Flüssigkeiten
Definition:
Aggregatzustände
Fest (niedrige Temp.):
formstabil, elastisch, kann
brechen (spröde); häufig
geordneter Aufbau
Druck ist Kraft pro Fläche
F
Kolben
(Fläche A)
Atome
p=
F
A
Einheit Pascal
Flüssigkeit
(oder Gas)
[Pa] = [N/m2]
(105 Pa = 1 bar)
Bindungen
Flüssigkeiten und Gase geben Druck weiter; in einem Behälter mit
ruhendem Medium wirkt auf alle Flächen derselbe Druck
(Schwerkraft vernachlässigt).
Flüssig (mittlere Temp.): ähnliche Dichte wie fester
Zustand, volumenelastisch,
nicht formstabil;
ungeordneter Aufbau
6.1.1 Hydraulik
Der gleichmässige Druck in einem Behälter läßt sich zur KraftWeitergabe und Kraft–Verstärkung ausnutzen.
Druck im Behälter:
Gasförmig (hohe Temp.): geringe Dichte, sehr
kompressibel;
ungeordnet, keine Bindungen
F1
Fläche
A1
F2
p=
Fläche
A2
F1
A1
Kraft auf zweiten Kolben:
F2 = pA2 =
A2
F1
A1
76
77
6.1.2 Schweredruck
Die Kraft kann also beliebig verstärkt werden!
Im Schwerefeld entsteht Druck aufgrund der Masse einer
Flüssigkeit (bzw. eines Gases)
Frage: läßt sich so Energie gewinnen?
Berechnung der geleisteten Arbeit:
g
Kolben 1 bewege sich um Strecke l1 ; dabei wird ein Volumen
bewegt von
V1 = l1 A1
h
oberer Teil
der Flüssigkeit
wirkt als
„Kolben“
Wenn die Flüssigkeit als inkompressibel angenommen wird,
bewegt sich Kolben 2 damit um:
l2 =
V2 V1
=
A2 A2
W1 = l1F1
Kolben 2:
W2 = l2 F2 =
⇒
F ρVg ρhAg
=
=
A
A
A
p = ρhg
Der Druck nimmt linear mit
der Tiefe zu!
Flüssigkeit mit
Dichte ρ
V1 A2
F1 = l1F1
A2 A1
Die am Kolben 1 und vom Kolben 2 geleistete Arbeit ist
identisch; wie beim Flaschenzug läßt sich nur die Kraft
verstärken; die Arbeit (Kraft mal Weg) bleibt dieselbe!
Allgemein: die Volumenarbeit an Flüssigkeiten oder
Gasen ist gegeben durch
V
W = lF = F = pV
A
p=
Fläche A
Geleistete Arbeit:
Kolben 1:
Druck in der Tiefe h (äußerer
Druck vernachlässigt:
Beispiel: für Wasser ist ρ = 1000 kg/m3; damit ist
N
p = 9810  3  h
m 
Der Druck im Wasser steigt also alle 10 m Wassertiefe um etwa
105 Pa oder 1 bar.
Senkrecht zur Schwerkraft ist der Druck konstant (aufgrund des
gleichmässigen Drucks innerhalb einer Flüssigkeit)
V2
bzw.
W = ∫ p(V )dV
V1
⇒ der Druck in einem beliebigen Gefäß hängt nicht von der
Form des Gefäßes, sondern nur vom senkrechten Abstand zur
Flüssigkeitsoberfläche ab!
78
6.1.3 Auftrieb
79
Damit gilt für die Auftriebskraft eines Körpers in einer Flüssigkeit
im Schwerefeld:
Jeder Körper in einer Flüssigkeit im Schwerefeld erfährt eine
Auftriebskraft.
äußerer
Druck p0
Fläche
A
F2
F1
g
h2
Kraft auf untere Fläche
F1 = ( p1 + p0 ) A = ( ρh1 g + p0 ) A
h1
Kraft auf obere Fläche
F2 = ( p2 + p0 ) A = ( ρh2 g + p0 ) A
F1 − F2 = ρgA(h1 − h2 ) = ρgV
V: Volumen des Quaders
Die Auftriebskraft entspricht der Gewichtskraft der von dem
Körper verdrängten Flüssigkeit!
6.1.4 Oberflächenspannung
Um eine neue Oberfläche zu erzeugen,
müssen Bindungen gebrochen werden.
Die aufzubringende Energie ist proportional
zur erzeugten Fläche:
Es wirkt also eine nach oben gerichtete Kraft, die dem Volumen
des Quaders und der Dichte der Flüssigkeit proportional ist
(die Kräfte auf die Seitenflächen kompensieren sich, da der Druck
auf gleicher Höhe gleich ist).
EOF = σ A
A : Fläche
σ : Oberflächenspannung
Gilt für beliebige Körper:
diese lassen sich in senkrechte Quader
aufteilen; die gesamte Auftriebskraft
ist dann
n
n
i =1
i =1
F = ∑ Fi = ∑ ρgVi = ρgV
Auftriebskraft
ρ: Dichte der Flüssigkeit
V: Volumen des Körpers
Für einen senkrechten Quader gilt:
Quader in Flüssigkeit
Differenz:
FA = ρgV
neue
Oberflächen
gebrochene
Bindungen
Beispiel: Kraft auf einen benetzten Bügel
b
F
∆x
Flüssigkeit
Flüssigkeitsfilm
Eine Verschiebung um ∆x
vergrößert die Oberfläche
des Films:
∆ A = 2b∆x
(der Film hat zwei Oberflächen!)
80
Oberflächenenergie:
81
6.1.5 Strömungen
∆ E = σ∆A = σ 2b∆x
Strömungen haben ortsabhängige Geschwindigkeiten:
Geleistete Arbeit also:
v = v (r )
∆W = F∆x = σ 2b∆x
Damit ist die Kraft:
F = 2σ b
Massenstromdichte:
v
erlaubt Messung der
Oberflächenspannung!
j = ρ ( r )v ( r )
ρ: Massendichte
Einheit der Stromdichte:
Beispiel: Druck in Seifenblase
gesamte Oberfläche des Films:
pa
A = 4πr 2
Massenfluß durch eine Fläche A:
2
r
φ = jA
( = jA
(zwei Grenzflächen!)
pi
dA
= 16πr
dr
Ableitung nach r:
Änderung von A bei Änderung von r um dr:
A1
A2
v1
dE = σdA = σ 16πrdr
Der Massenfluß durch A1 und A2 muss
gleich sein
φ1 = φ2
j1 A1 = j2 A2
v2
Vom Gas in der Blase geleistete Arbeit:
dW = ( pi − pa )dV = ( pi − pa )4πr dr
falls j ⊥ A)
Für eine inkompressible Flüssigkeit ist die Massendichte
ortsunabhängig. Damit gilt bei einer Änderung des Querschnitts
eines durchströmten Rohrs:
dA = 16πrdr
Damit verbundene Änderung der Oberflächenenergie:
 kg 
 m 2s 
ρv1 A1 = ρv2 A2
Flüssigkeit
2
also
Im Gleichgewicht ist dies gleich dE:
dE = dW
⇒
pi − pa =
4σ
r
Druckdifferenz
zwischen innen
und außen
bzw.
v2 =
A1
v1
A2
v1 A1 = v2 A2
„Kontinuitätsgleichung“
Die Strömungsgeschwindigkeit nimmt an
Engstellen zu!
82
6.1.6 Bernoulli-Gleichung
83
allgemein:
1
p + ρv 2 = konstant = p0
2
In einer Strömung einer inkompressiblen Flüssigkeit (oder eines
Gases) sind Druck und Strömungsgeschwindigkeit direkt
miteinander verknüpft.
A1
v1
p1
p2
A2
v2
Rohr mit Verjüngung:
das in einer Zeit ∆t eintretende
Volumen ist gleich dem
austretenden Volumen:
∆V1 = ∆V2 = ∆V
Bernoulli-Gleichung
Der Druck in einer Strömung nimmt mit der Geschwindigkeit ab!
6.1.7 Flüssigkeit mit innerer Reibung
z
v
An der Flüssigkeit wird am Eintritt Arbeit geleistet:
Fläche
A
∆W1 = p1 A1∆x1
Für die Reibungskraft zwischen
zwei Flächen, zwischen denen sich eine
viskose Flüssigkeit befindet, gilt:
F = − Aη
Am Austritt leistet die Flüssigkeit Arbeit:
∆W2 = p2 A2 ∆x2
η: Viskositätskonstante
A: Flächengröße
v: relative Geschwindigkeit
z: Abstand
Flüssigkeit
Der Volumenfluß erzeugt einen Zu- und Abfluß kinetischer Energie:
1
∆E1 = ρ∆V1v12
2
1
∆E2 = ρ∆V2v22
2
Im Gleichgewicht muss die Energiebilanz ausgeglichen sein:
∆E1 + ∆W1 = ∆E2 + ∆W2
also
1
1
ρ∆Vv12 + p1∆V = ρ∆Vv22 + p2 ∆V
2
2
1 2
1
ρv1 + p1 = ρv22 + p2
2
2
v
z
Die Kraft wirkt der Bewegung entgegen, daher das Minuszeichen
(häufig wird nur der Betrag der Kraft angegeben).
Diese Reibungskraft tritt auch zwischen Flüssigkeitsschichten
auf; hier gilt das obige Gesetz in differentieller Form:
F = − Aη
dv
dz
Die innere Reibung bestimmt das Geschwindigkeitsprofil
einer Strömung.
84
Beispiel: rundes Rohr
p1
Betrachten ein Teilvolumen
mit Radius r, welches sich mit der
Geschwindigkeit v der Strömung bei
r bewegt.
Teilvolumen
Auf dieses wirkt die Reibungskraft:
v
Rohr
L
Fp = ( p1 − p2 )πr 2
r0
Also:
strömende
Flüssigkeit
η 2πrL
⇒
dv
= −( p1 − p2 )πr 2
dr
dv
∆p
=−
r
dr
2ηL
Dies gilt für Teilvolumina aller Radien; damit läßt sich das
Geschwindigkeitsprofil im Rohr durch Integrieren berechnen
v(r ) = −
∆p 2
r + v0
4ηL
Da die Geschwindigkeit an der Rohrwand (r = r0) Null sein muss,
gilt
v(r ) =
Der Gesamtfluß durch das Rohr ergibt sich durch Integration des
Strömungsprofils:
ρ∆pπ
(r02 − r 2 )rdr
φ = ∫ ρv(r )2πrdr =
∫
2ηL 0
0
r0
∆p 2 2
(r0 − r )
4ηL
r0
=
dv
dv
FR = ηA = η 2πrL
dr
dr
Diese muss durch die Differenz
der Druckkräfte auf das Teilvolumen
aufgebracht werden:
p2
85
⇒
ρ∆pπ 1 4 1 4 ρ ∆pπ 1 4
( r0 − r0 ) =
r0
4
2ηL 4
2ηL 2
φ=
ρπ∆p 4
r0
8ηL
Hagen-Poisseuille
Der Gesamtfluß durch ein Rohr bei gegebener Druckdifferenz
und Rohrlänge ist proportional zur vierten Potenz des Rohrradius!
86
87
Das Kraftgesetz gilt nur für geringe Verformungen; bei größereren
Spannungen erfolgt der Übergang von elastischer zu plastischer
(permanenter) Verformung.
6.2 Deformierbare feste Körper
6.2.1 Kraftgesetze
Definition: mechanische Spannung
Stab
F
σ=
A
∆l
l
F
N
 m 2 
σ
Beispiel Kupfer
( E = 120 109 Pa)
N
 m 2 
plastisch
108
(negativer Druck)
Fläche A
reisst
elastisch
Für die Längenänderung des Stabs gilt:
∆l σ
1
= =
F
l E EA
bzw.
σ =E
1 10-3
3 10-3
0.1
Hook‘sches
Gesetz
∆l
l
Weitere Verformungen
E: Elastizitätsmodul (Materialkonstante)
Körper unter Druck
Kompression
Die Längenänderung ist proportional zur Kraft!
F
Volumenabnahme
p
∆V
= −κ p
V
Andere Schreibweise: die Gegenkraft ist gegeben durch
F =−
2 10-3
EA
∆l = − D∆l
l
D: Federkonstante
F
F
κ : Kompressibilität
∆l
l
88
Scherung
A
Tangentiale Kraft auf Fläche:
Schubspannung
F
τ=
α
F
A
N
2
 m 
Die Schubspannung erzeugt eine Scherung
um den Winkel α:
α=
1
τ
G
G : Torsionsmodul
Drillung
T
Das Drehmoment erzeugt einen
Verdrillungswinkel α
α=
α
1
2l
T=
T
DR
π GR 4
DR: Richtgröße
Für alle Verformungen gilt: die Verformung ist proportional
zur Kraft für kleine Verformungen! Die potentielle Energie
ist damit proportional zum Quadrat der Verformung.