Aufstellen der Bewegungsgleichungen der harmonischen

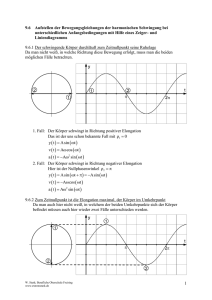
9.6
Aufstellen der Bewegungsgleichungen der harmonischen Schwingung bei
unterschiedlichen Anfangsbedingungen mit Hilfe eines Zeiger- und
Liniendiagramms
9.6.1 Der schwingende Körper durchläuft zum Zeitnullpunkt seine Ruhelage
Da man nicht weiß, in welche Richtung diese Bewegung erfolgt, muss man die beiden
möglichen Fälle betrachten.
2
2

1
1
2
1. Fall: Der Körper schwingt in Richtung positiver Elongation
Das ist der uns schon bekannte Fall mit 1  0
y  t   Asin  t 
v  t   A cos  t 
a  t   A2 sin  t 
2. Fall: Der Körper schwingt in Richtung negativer Elongation
Hier ist der Nullphasenwinkel 2  
y  t   Asin  t    Asin  t 
v  t   A cos  t 
a  t   A2 sin  t 
9.6.2 Zum Zeitnullpunkt ist die Elongation maximal, der Körper im Umkehrpunkt
Da man auch hier nicht weiß, in welchem der beiden Umkehrpunkte sich der Körper befindet
müssen auch hier wieder zwei Fälle unterschieden werden.
1
1

2
2
2
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
1
1. Fall: Der Körper befindet sich im oberen Umkehrpunkt
Hier gilt für den Nullphasenwinkel 1  2
y  t   Asin  t  2   A cos  t 
v  t   A sin  t 
a  t   A2 cos  t 
2. Fall: Der Körper befindet sich im unteren Umkehrpunkt
Hier gilt für den Nullphasenwinkel 2  32
y  t   Asin  t  32   A cos  t 
v  t   A sin  t 
a  t   A2 cos  t 
9.6.3 Allgemeiner Fall
Hier ist in der Regel ein Wert für die Elongation  y  0   23 A  zum Zeitpunkt t  0 gegeben.
Wie unschwer zu erkennen ist, sind zwei Fälle zu unterscheiden.
1. Fall: Allgemein gilt: y  t   Asin  t  1 
y  0   A sin  1   23 A  sin  1  
2
3
 1  41,8 Winkelmaß (TR auf DEG)
 1  0, 730 Bogenmaß (TR auf RAD)
y  t   Asin  t  0,730 
1
2
2
1

2
2. Fall: Die zweite Lösung erhält man nun aus dem Zeigerdiagramm, denn es gilt:
2    1  2, 412  2  138, 2 
y  t   Asin  t  2, 412 
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
2
Aufgaben
2.0 Zum Zeitpunkt t  0 befindet sich die Pendelmasse mit 50% der Amplitude oberhalb der
Nulllage auf dem Weg nach oben.
2.1 Berechne den Nullphasenwinkel 0 !
 y  0  A  sin   
A  0  arcsin  0,5  6 
Wie wäre die Phasenverschiebung, wenn sich die Pendelmasse auf dem Weg nach unten
befindet?  0    6  56 
0
1
2
2.2 Die Amplitude der Schwingung betrage 30cm und die Periodendauer sei T  1, 40s . Gib
die Zeit-Orts-Funktion an und berechne die Startgeschwindigkeit der Masse.
 y  t   0,3m  sin  4, 49  st  6  ; v(t)  1,35 ms  cos  4, 49  st  6  ; v 0  1, 2 ms 
2.3 Welche Elongation (Geschwindigkeit und Beschleunigung) erhält man nach 1, 0s ? Wo
befindet sich die Pendelmasse und in welche Richtung bewegt sie sich?
 y(1,0s)  0, 29 m; v(1,0s)  0,39
m
s
; a(1,0s)  5,8 sm2

 Pendel befin det sich unterhalb der Ruhelage und bewegt sich nach oben.
2.4 Zu welchem Zeitpunkt beträgt die Elongation zum ersten mal 10cm ?
arcsin   13   6
y  t R   0,3m  sin 4, 49  tsR  6  0,1m  t R 
 0,19s
4, 49 1s
 6
y  t N   0,3m  sin 4, 49  tsN  6  0  t N 
 0,12s
4, 49 1s




t Ges
tR
tN
t Ges  t N  12 T  t N  t R  0,12s  12 1, 4s  0,12s  (0,19s)  0,65s
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
3
2.5 Zu welchem Zeitpunkt ist der Betrag der Geschwindigkeit zum ersten mal
Maximal?
v  t R   1,35 ms  cos 4, 49 tsR  6  1,35 ms  v max  cos 4, 49 tsR  6  1




 4, 49 tsR  6  0  t R  0,12s
t Ges  t R  12 T  0,12s  0, 70s  0,58s
2.6 Zu welchen Zeiten befindet sich die Pendelmasse im oberen Umkehrpunkt?
v  t R   1,35 ms  cos 4, 49 tsR  6  0  cos 4, 49 tsR  6  0




 4, 49 tsR  6  2  t R  0, 23s
t O  0, 23s  n 1, 40s mit n  IN
2.7 Zu welchen Zeiten durchläuft die Pendelmasse die Ruhelage?
 t N  0,58s  n2  T  0,58s  n  0,70s; n  IN 
3.0 Ein harmonisch schwingender Körper befindet sich zum Zeitpunkt t  0 im unteren
(negativen) Umkehrpunkt.
3.1 Stelle allgemein die Bewegungsgleichung für Elongation, Geschwindigkeit und
Beschleunigung des Körpers in Abhängigkeit von der Zeit auf.
y  t   Asin  t  32   A cos  t 
v  t   A sin  t 
a  t   A2 cos  t 
3.2 Zeichne für t  0 das Zeigerdiagramm für Elongation, Geschwindigkeit und
Beschleunigung in ein Diagramm! (Zeigerlängen beliebig wählbar)
a
v
y
3.3 Zeichne für 0  t  T das Liniendiagramm für Elongation, Geschwindigkeit und
Beschleunigung in ein Diagramm! (passend zu den in 3.2 gewählten Zeigern)
a(t)
T
T
2
v(t)
y(t)
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
4
3.4 Gegeben sei A  0,50 m und T  1,0s . Berechne s, v und a für den Zeitpunkt t  1,3s .
y  t   0,5m  cos  2s t 
y 1,3s   0,5m  cos  2s 1,3s   0,15m

v  t    ms  sin  2s  t 
a  t   19,7 sm2  cos  2s  t 
4.0
4.1
v 1,3s    ms  sin  2s 1,3s   3,0 ms

a 1,3s   19,7 sm2  cos  2s 1,3s   6,1 sm2

Ein Körper schwingt harmonisch mit der Schwingungsdauer T  1,3s und der
Amplitude A  12cm . Zum Zeitpunkt t  0 bewegt er sich nach unten und hat die
Elongation y0  9,5cm .
Wie groß ist der Nullphasenwinkel?
y(t  0)  0,12m  sin 0  0, 095m  0  arcsin 0,095
0,12  0,91
0    0    0,91  2, 23
4.2 Gib die Schwingungsgleichung an!
2
y(t)  0,12m  sin  1,3s
 t  2, 23
4.3
Zu welchem Zeitpunkt t1 hat der Körper zum 2. Mal die Elongation y1  5,6cm
erreicht?
2
y(t E )  0,12 m  sin  1,3s
 t E  2, 23   0, 056 m
2
1,3s
 t E  2, 23  arcsin 0,056
0,12
1,3s
t E   arcsin 0,056
0,12  2, 23   2   0,56s
t1  t  T  0,56s  1,3s  0,74s
4.4 Zu welchen Zeitpunkten t 2 und t 3 erreicht er diese Elongation zum 3. und 4. Mal?
t 3  t1  T  0,74s  1,3s  2,04s
2
y(t N )  0,12m  sin  1,3s
 t N  2, 23   0
2
sin  1,3s
 t N  2, 23  0
2
1,3s
 t N  2, 23  0
t N  2, 23  1,3s
2   0, 46s
t 2  t1  12 T  2 t E  t N  0,74s  12 1,3s  2 0,56s  (0, 46s)  1,59s
Aufgabe mit einer Bewegung, die im unteren Umkehrpunkt beginnt. Wann ist die
Geschwindigkeit zum ersten mal 12 vmax und welche Strecke hat der Körper bis zu diesem
Zeitpunkt zurückgelegt?
Bei der Beschreibung der Bewegungen am Kreis bzw. bei der Schwingung treten gleiche
Größen mit verschiedenen Bedeutungen auf.
Größe
Kreisbewegung
r; A; ŷ ; ŝ Kreisbahnradius
T
Umlaufdauer
1
Frequenz
fT

Drehwinkel
Winkelgeschwindigkeit
  2f
W. Stark; Berufliche Oberschule Freising
www.extremstark.de
Schwingung
Amplitude
Perioden- bzw. Schwingungsdauer
Frequenz
Phasenwinkel
Kreisfrequenz
5