Hydromechanik und Thermodynamik Inhaltsverzeichnis

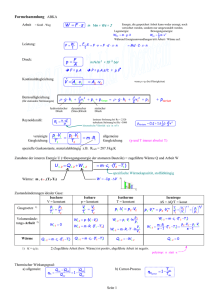
Skript zum Ferienkurs
Physik für Elektroingenieure
Wintersemester 2015 / 16
Nr. 4
Katrin Oberhofer
17.03.2016
Hydromechanik und Thermodynamik
Inhaltsverzeichnis
Hydromechanik und Thermodynamik
1
1
Definition des Fluids
2
2
Arten von Fluiden
2
3
Hydrostatik
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3
Dichte & Druck . . . . . . . . . . . . . . .
Pascalsches Prinzip . . . . . . . . . . . . .
Schweredruck, Hydrostatisches Paradoxon
Barometrische Höhenformel . . . . . . . .
Auftrieb . . . . . . . . . . . . . . . . . . .
Hydraulik . . . . . . . . . . . . . . . . . .
Kompressibilität . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
3
4
4
5
5
4
Oberflächenspannung
5
5
Hydrodynamik
7
5.1
5.2
5.3
5.4
5.5
5.6
5.7
Strömungen . . . . . . . . .
Kontinuitätsgleichung . . .
Bernoulligleichung . . . . .
Gesetz von Toricelli . . . . .
Viskosität . . . . . . . . . .
Gesetz von Hagen-Poiseuille
Strömungswiderstand . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
8
8
9
10
10
12
6
Stoffmenge, Avogadrogesetz
7
Ideales Gas
13
7.1 Die ideale Gasgleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
8
9
13
Innere Energie und Wärme
14
8.1 Wärme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8.2 Innere Energie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8.3 Kinetische Gastheorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
14
15
Thermodynamische Systeme
16
9.1 Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.2 1. Hauptsatz der Thermodynamik . . . . . . . . . . . . . . . . . . . . . . . . .
16
17
9.3 Zustandsänderungen
9.3.1 Isobare . . .
9.3.2 Isochore . . .
9.3.3 Isotherme . .
9.3.4 Adiabaten . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
10 Entropie
10.1 (Ir)Reversible Prozesse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10.2 2. Hauptsatz der Thermodynamik . . . . . . . . . . . . . . . . . . . . . . . . .
11 Kreisprozesse
11.1 Carnotscher Kreisprozess . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11.2 Wirkungsgrad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12 Reales Gas
17
17
18
18
19
20
20
20
21
21
23
23
Hydromechanik
1 Definition des Fluids
Die Hydrodynamik bezeichnet die Mechanik von flüssiger oder gasförmiger Materie. Die
Unterscheidung von Festkörpern und Fluiden erfolgt durch die Betrachtung der Wirkung
kleinster Scherspannungen. Festkörper reagieren auf Scherspannungen mit einer endlichen
Abbildung 1: Wirkung von Scherspannungen auf Festkörper und Fluide
Verformung und nehmen die ursprüngliche Form wieder an, wenn die Scherspannung weg
ist. Fluidpartikel können sich frei gegeneinander bewegen und fließen unter der kleinsten
tangentialen (Scher-) Kraft. Sie reagieren auf Scherspannungen mit einer endlichen Verformungsgeschwindigkeit.
2 Arten von Fluiden
Man unterscheidet zwei Arten von Fluiden:
• Gase sind Fluide mit schwachen Anziehungskräften zwischen den einzelnen Fluidpartikeln. Ein Gas füllt stets den ganzen zur Verfügung stehenden Raum in einem Behälter
aus und bildet keine freie Oberfläche.
• Flüssigkeiten sind Fluide mit starken Anziehungskräften zwischen den einzelnen Fluidpartikeln. Sie behalten Ihr Volumen bei und bilden freie Oberfläche sogar gegen Vakuum aus.
3 Hydrostatik
3.1 Dichte & Druck
Die Massendichte ρ von Materie bezeichnet das Verhältnis der schweren Masse m und des
Volumens V eines Körpers.
ρ=
m
V
Als Einheit dient die Kombination der SI Einheiten kg/m3 . Oftmals wird auch die Einheit
g/cm3 verwendet (Umrechnungsfaktor 1000).
Der Druck ist definiert als die auf eine Oberfläche A senkrecht wirkende Kraft FN , oftmals
auch Normalkraft FN bezeichnet, geteilt durch durch die Oberfläche A.
p=
FN
A
Als Einheit dient im SI-System das sogenannte Pascal, welches als das Verhältnis von den
Einheiten der Kraft, dem Newton N, und der Fläche definiert ist.
1Pa (Pascal) = 1
N
m2
In der Praxis ist oft die Einheit bar 1bar = 100kPa gebräuchlich.
3.2 Pascalsches Prinzip
Das Pascalsche Prinzip besagt, dass sich Druck in Fluiden ungehindert auf jeden Punkt in der
Flüssigkeit ausbreitet. Veranschaulicht wird dies im Versuch der kommunizierenden Röhren.
Abbildung 2: Veranschaulichung des Pascalschen Prinzips
Die Höhe der Wassersäule ist in allen verbundenen Röhren gleich.
3.3 Schweredruck, Hydrostatisches Paradoxon
Eine Flüssigkeitssäule der Höhe h und dem Querschnitt A hat die schwere Masse m = ρhA
und übt auf ihren Boden die Gewichtskraft F = mg = gρhA aus. Der auf den Boden wirkende
Druck p wird als Schweredruck bezeichnet.
(1)
p = ρ·g·h
Diese Gleichung gilt für alle Gefäße unabhängig von ihrer spezifischen Form. Der Schweredruck ist deshalb nur von der Höhe der Fluidsäule abhängig und nicht von der Menge des
aufgestauten Fluids!
Abbildung 3: Darstellung des hydrostatischen Paradoxons.
Der Schweredruck ist überall am Boden des Gefäßes gleich und entspricht dem Druck
der gesamten Fluidsäule h. Das Kräftegleichgewicht an den Wänden des ruhenden Gefäßes
erzeugt eine dem Innendruck entgegengesetzte Kraft auf das Fluid.
3.4 Barometrische Höhenformel
In Gasen ist aufgrund der hohen Kompressibilität die Dichte ρ druckabhängig. Für die Berechnung des Luftdrucks als Funktion der Höhe in der Erdatmosphäre muss diese Druckabhängigkeit berücksichtigt werden. Die Gleichung für den Schweredruck gilt dann nur für eine
dünne Schicht h2 − h1 → dh.
dp = − g · ρ · dh
bei konstanter Temperatur gilt:
p
p
= 0
ρ
ρ0
Durch Einsetzen und integrieren ergibt sich die barometrische Höhenformel
p(h) = p0 e− gρ0 h/p0
3.5 Auftrieb
Der Schweredruck des Wassers wirkt auf alle Seitenflächen eines im Wasser schwebenden
Körpers mit Querschnitt A und Höhe h. Die Kräfte auf den Seitenflächen heben sich auf. Die
Kräfte auf Grund- und Deckfläche des Körpers hängen von deren Tiefe ab.
Abbildung 4: Auftriebskraft
Als Auftriebskraft ergibt sich die Differenz der Kräfte auf Grund- und Deckfläche.
Fa = F1 − F2 = ρgh1 A − ρgh2 A = ρgV
Der Auftrieb entspricht also der Schwerkraft des durch den Körper verdrängten Wassers. Für
die Frage ob ein Körper im Wasser schwebt, sinkt oder an die Oberfläche steigt ist also allein
dessen Dichte relevant. Ragt ein Teil des Körpers aus dem Wasser heraus so trägt dieses Volumen nicht zum Auftrieb bei und es stellt sich ein Kräftegleichgewicht zwischen Schwerkraft
und Auftriebskraft ein.
3.6 Hydraulik
Das Pascalsche Prinzip kann analog zu den Hebelgesetzen eingesetzt werden um mechanische
Kräfte zu übersetzten. Veranschaulicht wird dies in der Wirkung einer Hydraulischen Presse:
Abbildung 5: Hydraulische Presse
Nach dem Pascalschen Prinzip ist der Druck in beiden Behältern gleich. Wirkt nun eine
Kraft F1 = p · A1 auf den kleineren Zylinder, so ergibt sich bei konstantem Druck p eine Kraft
auf den größeren Zylinder F2 = p · A2 .
F2 =
A2
· F1
A1
Die durch diese Kraft verrichtete Arbeit wird als Druckarbeit W bezeichnet
W1 = F1 · ∆x1 = p · A1 · ∆x1 = p · ∆V.
Unter Vernachlässigung von Reibung, d.h. W1 = −W2 , und für inkompressible Flüssigkeiten,
d.h. ∆V1 = −∆V2 , folgt dann das hydraulische Hebelverhältnis:
x2 =
A1
· x1
A2
3.7 Kompressibilität
Reale Fluide können durch die Ausübung von Druck komprimiert werden. Die Kompressibilität κ eines Materials ist definiert als die relative Volumenänderung pro Druckänderung
κ=−
1 dp
V dV
Die Kompressibilität eines Fluids ist abhängig von seiner Art und seinen Zustandsgrößen wie
Druck und Temperatur. Dabei sind Flüssigkeiten durch eine geringe Kompressibilität charakterisiert. Gase hingegen sind aufgrund der geringen Teichendichte in hohem Maße kompressibel.
4 Oberflächenspannung
Eine Flüssigkeit wird durch die Anziehungskraft zwischen den Molekülen zusammengehalten. Auf Moleküle im Inneren der Flüssigkeit hebt sich die Summe der Kräfte zu den anderen
Molekülen im zeitlichen Mittel auf. Auf Moleküle an der Phasengrenzfläche ergibt sich eine
Summenkraft, die in die Flüssigkeit hinein gerichtet wirkt.
Abbildung 6: Darstellung der Oberflächenspannung
Die Oberflächenspannung σ versucht die Oberfläche A des Fluids möglichst klein zu halten.
Sie ist definiert als die pro Flächenzuwachs dA zu verrichtende Arbeit dE
dE = σdA.
Diese Energieänderung erzeugt eine Kraft die entgegen der Vergrößerung der Oberfläche
wirkt.
Ziehen wir den Balken nach rechts verrichten wir gegen die Oberflächenspannung Arbeit.
∆W = F∆x
Die Vergrößerung der Oberfläche ist
∆A = 2l · ∆x
Daraus kann die Randkraft berechnet werden.
F = 2l · σ
Die Randkraft ist also proportional zum Umfang und zur Oberflächenspannung.
Für die Grenzfläche zwischen Flüssigkeiten und Festkörpern, kann die Energieänderung
positiv oder negativ sein, je nachdem ob die Anziehungskräfte zwischen Flüssigkeitsmolekülen und dem Festkörper kleiner oder größer ist als zwischen den Molekülen der Flüssigkeit.
Aus der durch die Oberflächenspannung resultierenden Kraft folgt der Kapillareffekt, d.h.
das Ansteigen oder Absinken von Flüssigkeit in dünnen Rohren. Dies führt zur Ausbildung
von Tropfen auf Oberflächen oder zur Benetzung des Festkörpers mit der Flüssigkeit. Ein
quantitatives Maß für das Verhalten einer Flüssigkeit auf einer Festkörperoberfläche ist der
Kontaktwinkel Φ.
Die Steigungshöhe im Rohr kann aus dem Gleichgewicht von Gewichtskraft und Oberflächenkraft(Randkraft) berechnet werden:
hkap =
2σ
cos(Φ)
ρgr
Abbildung 7: Kapillareffekt für Flüssigkeiten unterschiedlichen Kontaktwinkels in einem dünnen Glasröhrchen
5 Hydrodynamik
5.1 Strömungen
Die Hydromechanik beschreibt die Bewegungen von Fluiden als Wirkungen innerer und äusserer Kräfte und Spannungen. Die Bewegung einen Fluids wird auch als Strömung bezeichnet. Mathematisch können Strömungen z.B. im Bild der Massenpunkte verstanden werden.
Dabei hat jeder Massepunkt des Fluids eine individuelle Bahn.
• Stromfaden: Die Bahn eines individuellen Massepunktes
• Stromlinie: Gesamtheit der Vektoren der Geschwindigkeiten an allen Punkten des Stromfadens
Für stationäre Strömungen, d.h. die Stromlinien sind nicht von der Zeit abhängig, sind
Stromfaden und Stromlinien identisch. Stationäre Strömung bedeutet nicht, dass sich die
Geschwindigkeit eines Massepunktes nicht mit der Zeit ändert.
Man unterscheidet hierbei zwischen zwei allgemeinen Fällen:
• Laminare Strömung: Bei kleinen Geschwindigkeiten und starker innerer Reibung des
Fluids richten sich die die Stromlinien so parallel wie möglich aus. (Wasser in dünnem
Rohr)
• Turbulente Strömung: Bei hohen Geschwindigkeiten und schwacher innerer Reibung
bilden sich Verwirbelungen der Stromlinien. (Luftumströmung eines Fahnenmasten)
Abbildung 8: Darstellung von Stromlinien laminarer und turbulenter Strömung
5.2 Kontinuitätsgleichung
Für stationäre Strömungen gilt: Durch jeden Punkt im Rohr muss in derselben Zeit die gleiche
Menge an Flüssigkeit strömen. Das heißt der Massenstrom dM/dt = ρAv ist eine Erhaltungsgröße.
Abbildung 9: Darstellung der Kontinuitätsgleichung
Es gilt, dass die Masse dm des Volumenelementes A1 ds1 dass pro Zeitintervall dt durch
einen Querschnitt A1 fließt
(2)
dm = ρ1 · A1 ds1 = ρ2 · A2 ds2
eine konstante an allen Orten des Rohrs ist. Für inkompressible Fluide gilt weiterhin, dass die
Dichte an allen Orten und zu allen Zeiten konstant ist, d.h. ρ1 = ρ2 , und der Volumenstrom
(3)
dV
= A1 v1 = A2 v2 = const.
dt
ebenfalls Erhaltungsgröße ist. Man kann also die Fließgeschwindigkeit an allen Stellen im
Rohr sofort berechnen, wenn die Querschnitte und der Volumenstrom bekannt sind.
5.3 Bernoulligleichung
Für die stationäre Strömung und unter Vernachlässigung von Reibungskräften gilt der Energieerhaltungssatz. Das heißt die Summe aus potentieller Energie (Druck- und Lageenergie)
und kinetischer Energie ist erhalten. Für ein Massenelement ρdV folgt, dass Änderungen der
Lageenergie ρ · dV · g · h und der kinetischen Energie 1/2ρ · dV · v2 durch die Druckarbeit pdV
ausgeglichen werden.
Abbildung 10: Die grüne Flüssigkeitsmenge ist um y2 − y1 angehoben worden und wurde von
v1 auf v2 beschleunigt.
Es folgt also
1
pdV + ρdVv2 + ρdVgh = const.
2
Das unbekannte Volumenelement kann aus der Gleichung eliminiert werden und man erhält
die Bernoulligleichung.
1
p + ρv2 + ρgh = const.
2
(4)
Zusammen mit der Kontinuitätsgleichung ist damit der Druck an allen Stellen im Rohr durch
den Querschnitt und die Lage im Raum zu errechnen.
5.4 Gesetz von Toricelli
Abbildung 11: Darstellung des Gesetzes von Toricelli
Die Geschwindigkeit v des ausströmenden Wassers aus dem Loch B kann aus der Bernoulligleichung hergeleitet werden. Auf den beiden Ebenen A und B lastet jeweils der Atmosphärendruck p A = pB , da das Gefäß auf beiden Ebenen offen ist. Für die Geschwindigkeit des
ausströmenden Wassers folgt nun:
1
p A + ρgy A = pB + ρg(y A − h) + ρv2
2
Die Fließgeschwindigkeit im Behälter wird vernachlässigt (kleines Loch). Es folgt die Geschwindigkeit v des ausströmenden Wassers:
p
v = 2gh
Das gleiche Ergebnis folgt aus der Energieerhaltung.
5.5 Viskosität
Bisher haben wir die Mechanik der Fluide unter Vernachlässigung der Reibung betrachtet.
Die innere Anziehungskraft der Fluidpartikel führt zu Reibungskräften, wenn verschiedene
Flüssigkeitsschichten mit unterschiedlicher Geschwindigkeit aneinander vorbei strömen. Eine
konstante Geschwindigkeit kann nur durch ständiges Anlegen der treibenden Kraft erreicht
werden.
Abbildung 12: Geschwindigkeitsprofil einer viskosen Flüssigkeit bei laminarer Strömung zwischen planparallelen Platten
Wir betrachten die Bewegung einer Flüssigkeit zwischen zwei planparalellen Platten der
Fläche A, von denen eine mit konstanter Geschwindigkeit v bewegt wird. Es wird angenommen, dass die Flüssigkeit direkt an den Platten mit derselben Geschwindigkeit bewegt wird,
d.h. dass die erste Molekülschicht der Flüssigkeit an der Platte haftet. Ist die innere Reibungskraft unabhängig von der Fließgeschwindigkeit (Newtonsche Flüssigkeit), so stellt sich
ein lineares Geschwindigkeitsprofil ein. Als zum Antrieb notwendige Kraft Ft findet man
v
Ft = η A .
z
Die dynamische Viskosität wird mit η bezeichnet und ist eine Materialeigenschaft, die aber
stark von der Temperatur abhängt. Ihre Einheit ist Ns/m2 . Eine allgemeinere Formulierung
der viskosen Reibungskraft gelingt durch die Einführung der Schubspannung τ.
τ=
dFt
dvx
=η
dA
dz
5.6 Gesetz von Hagen-Poiseuille
Eine technisch bedeutsame Anwendung ist die Berechnung der laminaren Rohrströmung.
Abbildung 13: Kräftegleichgewicht der laminaren Rohrströmung
Wir betrachten ein Zylinderelement mit Radius r in einem Rohr der Länge l und Mantelfläche A = 2πrl. Die Kraft Fp des treibenden Drucks auf das Zylinderelement ist
Fp = πr2 (p1 − p2 ),
und gleicht der auf die Zylindermantelfläche wirkenden Reibungskraft
dv
dv
= η2πrl .
dr
dr
Durch Aufstellen des Kräftegleichgewichts Fp = Ft und lösen der Differentialgleichung mit
der Randbedingung, dass die Flüssigkeit am Rande des Rohres r = R ruht, erhält man das
Geschwindigkeitsprofil der laminaren Rohrströmung:
Ft = η A
v(r ) =
p1 − p2
· ( R2 − r 2 )
4ηl
Aus dem Geschwindigkeitsprofil kann man den Volumenstrom durch die Rohrleitung berechnen.
Abbildung 14: Darstellung des zylinderförmigen Volumenelementes und des parabolischen
Geschwindigkeitsprofils
Die Integration findet über die ringförmigen Volumenelemente der Dicke dr statt mit Volumenstrom
dV̇ = 2πrdrv(r ),
und es folgt der gesamte Volumenstrom
V̇ =
Z R
0
p1 − p2 2
2
2πr
· R − r dr
4ηl
Nach Lösen des Integrals und Umformung erhält man das Gesetz von Hagen-Poiseuille für
die laminare Rohrströmung.
V̇ =
π (p1 − p2 ) 4
R
8ηl
5.7 Strömungswiderstand
Werden Festkörper von Fluiden umströmt, so ergibt sich aufgrund der Reibungskräfte im
Fluid eine Kraft auf den Körper, welche als Strömungswiderstand bezeichnet wird. Hierbei
gibt es große Unterschiede zwischen laminarer Strömung und turbulenter Strömung. Die
Art der Umströmung eines Körpers hängt von vielen Faktoren ab, die in der sogenannten
Reynoldszahl zusammengefasst sind
Re =
vρL
,
η
wobei v die Strömungsgeschwindigkeit ist, ρ die Dichte des Fluids, L die charakteristische
Größe des Objekts senkrecht zur Flussrichtung und η die dynamische Viskosität.
Abbildung 15: Darstellung der Stromlinien turbulenter Umströmung einer Platte
Bei der turbulenten Strömung kann die Reibung über die Arbeit, die verrichtet werden
muss, um die Fluidpartikel von der Geschwindigkeit v auf 0 abzubremsen, errechnet werden.
v2
Ft = cW Aρ
2
Der Strömungswiderstandskoeffizient cW hängt von der Gestalt und der Oberfläche des Körpers sowie dem Turbulenzgrad der Strömung ab. Für die laminare Strömung ergibt sich analog zur Reibungskraft der ebenen Platte eine lineare Abhängigkeit von Reibungskraft und
Strömungsgeschwindigkeit.
Abbildung 16: Stromlinien der laminaren Umströmung einer Kugel
Ein Beispiel ist die Stokessche Reibungsformel für laminare Strömungen und kugelförmige
Körper.
Ft = 6πηrv
Thermodynamik
6 Stoffmenge, Avogadrogesetz
Gleiche Volumina idealer Gase enthalten bei gleichem Druck und bei gleicher Temperatur
gleich viele Moleküle. Ein Volumen von 22.4l eines idealen Gases unter Normalbedingungen
(p = 1013mbar, T = 273K ) enthält immer dieselbe Anzahl Atome oder Moleküle, nämlich
1Mol. In einem Mol befinden sich NA = 6.022 · 1023 Gasatome/-moleküle. Diese Zahl wird
als Avogadrokonstante bezeichnet.
7 Ideales Gas
Als ideales Gas bezeichnet man in der Physik eine idealisierte Modellvorstellung eines realen Gases. Zur Vereinfachung der physikalischen Betrachtung geht man von folgenden drei
Annahmen aus:
• Punktteilchen, d.h. Moleküle haben kein eigenes Volumen
• Keine Wechselwirkung zwischen den Teilchen
• Stöße der Moleküle untereinander und mit den Wänden sind elastisch
Der Zustand eines idealen Gases wird durch die Zustandsgrößen Volumen V, Druck p, absolute Temperatur T in K und die Teilchenzahl N beschrieben.
7.1 Die ideale Gasgleichung
Experimentiell findet man zwischen den Zustandsgrößen folgende Zusammenhänge:
a) Gesetz von Boyle und Mariotte (T = const. und N = const.):
p · V = const.
b) Gesetz von Gay-Lussac (p = const. und N = const.):
V
= const.
T
c) Gesetz von Amontons (V = const. und N = const.):
p
= const.
T
d) Ausserdem findet man für p = const. und T = const.
N
= const.
V
Aus diesen empirischen Beobachtungen, die jeweils für viele Gase über weite Temperatur und
Druckbereiche hervorragende Beschreibungen der makroskopischen physikalischen Situtaion
erlauben, folgt die Zustandsgleichung des idealen Gases
(5)
pV = Nk B T,
mit der Boltzmann-Konstante k B = 1.38 · 10−23 J/K. Statt der Teilchenzahl N kann die ideale
Gasgleichung auch mit der Molzahl ν = N/NA formuliert werden
(6)
pV = νRT,
wobei R = 8.314J/(mol · K ) als Gaskonstante bezeichnet wird. Es gilt
R
(7)
kB =
NA
Die Gaskonstante ist R = 8.314 J/(mol K ).
8 Innere Energie und Wärme
8.1 Wärme
Wärme ist die Energie, die von einem Körper zum anderen aufgrund einer Temperaturdifferenz übertragen wird. Wird den Teilchen eines Körpers durch Zufuhr von Wärme Q Energie
zugeführt, erhöht sich die Temperatur proportional zur zugeführten Wärme.
Q = C · ( T2 − T1 )
Hierbei ist C die Wärmekapazität mit Einheit J/K. Sie ist ein Maß daüfr, welche Wärmemenge
notwendig ist, um einen Körper um ein Grad Kelvin zu erwärmen. Die Wärmekapazität eines
Körpers geteilt durch die Masse des Körpers ergibt die spezifische Wärmekapazität c mit
Einheit J/(kgK ). Sie ist eine Materialkonstante und beschreibt die Fähigkeit eines Materials
aufgrund seiner atomaren Struktur Wärme aufzunehmen und zu speichern.
Für Gase muss zwischen der spezifischen Wärme bei konstantem Druck cp oder konstantem
Volumen cV unterschieden werden, weil bei der Ausdehnung des Gases bei konstantem Druck
Druckarbeit Wp = pdV verrichtet wird. Ihr Verhältnis
cp
κ=
cV
wird Adiabatenindex genannt. Aus der idealen Gasgleichung sehen wir, dass bei konstantem
Druck p bei einem Anstieg der Temperatur T auch das Volumen V ansteigt. Der Betrag der
vom Gas geleisteten Arbeit ist
|∆W | = p∆V
Diese Energie muss dem Gas zusätzlich zugeführt werden. Die Wärmekapazität ist höher. Bei
konstantem Volumen hingegen wird keine zusätzliche Arbeit verrichtet.
8.2 Innere Energie
Die innere Energie U eines Gases im Volumen V bezeichnet den gesamten Energieinhalt des
Volumens, soweit es vom inneren Zustand abhängt, d. h. die gesamte Energie seiner Moleküle. Voraussetzung ist, dass sich das Gas in Ruhe und im thermodynamischen Gleichgewicht
befindet.
Die innere Energie umfasst insbesondere:
• die thermische Bewegungsenergie der Gasteilchen,
• die chemische Energie der Moleküle, usw.
Wird das gesamte Volumen bewegt oder befindet sich in einem äußerem Potential, so werden diese makroskopischen Energien nicht zur inneren Energie gezählt, da sie von externen
Kräften abhängen.
8.3 Kinetische Gastheorie
Die kinetische Gastheorie leitet die makroskopischen Eigenschaften des idealen Gases aus
den mikroskopischen Bewegungen und Stößen der einzelnen Atome her. Der Schritt von
mikroskopischen, mechanischen Bewegungen zur makroskopischen thermodynamischen Zustandsgröße erfolgt durch Summation über alle ≈ 1023 Teilchen.
Der makroskopische Druck lässt sich durch den Impulsübertrag der Stöße der Gasteilchen
mit der Wand erklären. Die aufsummierte Impulsänderung aller Stöße pro Zeitintervall erlaubt dann die Berechnung von Kraft F und Druck p.
Abbildung 17: Molekül 1 führt in ∆t einen Wandstoß aus, der Impuls wird wegen des elastischen Stoßes an der Wand gespiegelt. Die Geschwindigkeit von Molekül 2
senkrecht zur Wand reicht nicht aus, um in ∆t die Wand zu erreichen.
Die Impulsänderung des einzelnen Stoßes ist
∆p = 2mvz .
Die Moleküle Z die im Zeitintervall ∆r die Wand mit Fläche A treffen sind höchstens vz ∆t
von der Wand entfernt.
Z=
1
N
Avz ∆t
V
2
Hierbei ist N/V die Teilchendichte, und der Faktor 1/2 berücksichtigt, dass nur die Hälfe
der Moleküle auf die Wand zu fliegen. Die gesamte Impulsänderung der Gasmoleküle beim
Wandstoß in ∆t ist:
∆pz = ∆pZ = Fz ∆t = pA∆t
Auflösen der Gleichung ergibt den kinematischen Druck:
N D E
p = m v2z
V
Die Klammern hi bezeichnen die Summation und Mittelung über alle Moleküle. Die Mittelung
und das Quadrat kommutieren nicht!
D E
v2 6 = h v i2
Die mittlere kinetische Energie eines Teilchens kann so mit den makroskopischen Zustandsgrößen in Bezug gebracht werden.
1 D E
1 D E D E D E
3 D E
Ēkin = m v2 = m v2x + v2y + v2z
= m v2z
2
2
2
Über die ideale Gasgleichung können die makroskopischen thermodynamischen Zustandsgrößen so mit der mikroskopischen Geschwindigkeit und kinetischen Energie in Bezug gebracht
werden. Einsetzten in die ideale Gasgleichung und vereinfachen liefert
Ēkin =
3
kB T
2
Die absolute Temperatur ist ein Maß für die Bewegungsenergie eines Moleküls. Die absolute
Temperatur 0K kann nicht erreicht werden, da immer langsamer werdende Moleküle immer
weniger Energie über Stöße abgeben können.
Es folgt die innere Energie des idealen Gases
U |V =const. = N · Ēkin =
(8)
3
3
Nk B T = νRT
2
2
und damit die Wärmekapazität bei konstantem Volumen
CV =
dQ
dU
3
=
= Nk B
dT
dT
2
Die Wärmekapazität bei konstantem Druck ist höher da zusätzlich Ausdehnungsarbeit verrichtet wird. Mit der Definition der inneren Energie und der idealen Gasgleichung folgt.
Cp =
dU pdV
3
5
dQ
=
+
= Nk B + Nk B = Nk B
dT
dT
dT
2
2
Und damit der Adiabatenexponent des idealen Gases.
κ=
Cp
= 1.4
CV
9 Thermodynamische Systeme
9.1 Definitionen
In der Thermodynamik unterscheidet man im Allgemeinen unter offenen, geschlossenen
und abgeschlossenen Systemen.
Abbildung 18: Darstellung offener, geschlossener und abgeschlossener Systeme
9.2 1. Hauptsatz der Thermodynamik
Die Änderung der inneren Energie ∆U eines Systems ist gleich der Summe der mit der Umgebung ausgetauschten Wärme ∆Q und der am System bzw. vom System verrichteten Arbeit
∆W.
(9)
∆U = ∆Q + ∆W bzw. dU = δW + δQ
Der erste Hauptsatz der Thermodynamik ist direkte Folge der Energieerhaltung und verbietet
die Konstruktion einer Maschine mit einem Wirkungsgrad größer eins.
9.3 Zustandsänderungen
Zustandsänderungen eines Systems können als Wege im Druck-Volumen-Diagramm (kurz pV-Diagramm) dargestellt werden. Die vom System geleistete Arbeit ist
(10)
δW = −p · dV
Die Vorzeichenkonvention ist wie folgt:
• δW < 0 Das System verrichtet Arbeit an seiner Umgebung (Expansion)
• δW > 0 Die Umgebung verrichtet Arbeit am System (Kompression)
Da V2 > V1 expandiert das Gas im System unseres Beispiels und verrichtet Arbeit am System.
Die Arbeit ist folglich
(11)
W1→2 = −
Z 2
pdV.
1
Aus dem p-V-Diagramm sieht man sofort, dass die Arbeit und somit auch die Wärme des Systems nicht nur von den beiden Endzuständen abhängen sondern auch vom Integrationsweg.
Im Folgenden diskutieren wir einige Spezialfälle der Zustandsänderung. Aus diesen kann
man alle technisch relevanten thermodynamischen Kreisprozesse (Carnot, Otto, Diesel, usw.)
konstruieren und berechnen.
9.3.1 Isobare
Ein isobarer Prozess beschreibt eine Zustandsänderung mit konstantem Druck (vgl. Gesetz
von Gay-Lussac). Die Isobare ist eine im p-V-Diagramm horizontale Linie.
Die innere Energie berechnet sich zu:
(12)
∆U12 = U2 − U1 = W12 + Q12
Im System zugefügte Arbeit:
(13)
W12 = −
Z 2
1
pdV = − p
Z 2
1
dV = − p(V2 − V1 )
Im idealen Gas ist Cp konstant und die Wärmeenergie folgt als
(14)
Q12 =
Z 2
1
Cp dT = Cp ∆T = C p
p∆V
νR
9.3.2 Isochore
Ein isochorer Prozess beschreibt eine Zustandsänderung mit konstantem Volumen (vgl. Gesetz von Antomons). Die Isochore ist eine im p-V-Diagramm vertikale Linie.
Zugeführte Wärme leistet keine Arbeit. Nur Erhöhung der inneren Energie, d.h. Temperaturerhöhung. Im idealen Gas ist CV konstant und die Wärmeenergie folgt als
Q12 = CV ( T2 − T1 ) = ∆U12
(15)
9.3.3 Isotherme
Ein isothermer Prozess findet bei konstanter Temperatur statt (vgl. Gesetz von Boyle und
Mariotte). Dies wird durch einen im Vergleich zum Prozess schnellen Wärmeaustausch mit
der Umgebung realisiert. Weil sich hierbei die innere Energie des idealen Gases ∆T ∝ ∆U = 0
nicht ändert, wird zugeführte Wärme direkt in Arbeit umgesetzt.
Die Berechnung der verrichteten Arbeit erfolgt durch Integration der idealen Gasgleichung:
(16)
W12 = −
Z 2
1
pdV = −
Z 2
νRT
1
V
dV = νRTln
V1
V2
Die freiwerdende Wärme folgt sogleich:
Q12 = −W12 = −νRTln
(17)
V1
V2
Die Isotherme ist eine Hyperbel im p-V-Diagramm.
9.3.4 Adiabaten
Adiabatische Prozesse finden ohne jeden Wärmeaustausch mit der Umgebung statt. Dies geschieht entweder, weil die Prozesse viel schneller vonstatten gehen als der Temperaturausgleich, oder wenn die Prozesse in einem abgeschlossenem System ablaufen.
Aus dem ersten Hauptsatz folgt mit ∆Q = 0
∆U12 = ∆W12 = CV ( T2 − T1 )
(18)
Wir können schreiben
δW = −pdV = −
νRT
dV
V
δU = CV dT
und es folgt nach Integration
ln
T2
νR V
= − ln 2
T1
CV V1
Für ideale Gase folgen mit dem Adiabatenindex κ = Cp /CV = 1 + (νR)/CV die Adiabatengleichungen
T · V κ −1 = const.
p · V κ = const.
Abbildung 19: Adiabaten und Isothermen im p-V-Diagramm
Bei der adiabatischen Expansion wird die mechanische Arbeit der inneren Energie entnommen. Die sinkende Temperatur hat einen niedrigeren Endruck zur Folge im Vergleich zur
äquivalenten isothermen Expansion.
10 Entropie
Die Entropie S ist eine thermodynamische Zustandsgröße, die wie Temperatur, Volumen und
Druck den Zustand eines Systems beschreibt. Die Entropie ist ein Maß für die Anzahl der
Mikrozustände, durch die der beobachtete Makrozustand des Systems realisiert werden kann
– anders ausgedrückt: Entropie ist ein Maß für die Unordnung eines Systems. Die Entropieänderung ist definiert als
dS =
dQ
T
Die Änderung der Entropie S in einem abgeschlossenen System (bleibt konstant oder steigt)
ist ein Maß für die Irreversibilität eines Vorgangs (reversibel/irreversibel).
Anmerkung: Adiabatische Zustandsänderungen sind durch dQ = 0 definiert. Die Entropie
S bleibt bei adiabatischen Zustandsänderungen konstant!
10.1 (Ir)Reversible Prozesse
Die Irreversibilität bestimmter Prozesse kann man z.B. für ideale Gase mit Hilfe des ersten
Hauptsatzes ∆U = ∆Q − p∆V berechnen.
dS =
dU pdV
dV
dT
dQ
=
+
= νCV
+ νR
T
T
T
T
V
Integrieren für konstantes CV gibt:
∆S = νCV · ln
T2
V
+ νR · ln 2
T1
V1
Ein Beispiel für einen irreversiblen Prozess ist die isotherme Expansion T2 = T1 des idealen
Gases.
Abbildung 20: Ein ideales Gas befindet sich zu Anfang ganz auf der linken Seite des Behälters.
Nach Entfernen der Wand strömt das Gas in den ganzen Behälter.
Die Entropieänderung ist somit
∆S = νR · ln
V2
>0
V1
10.2 2. Hauptsatz der Thermodynamik
Der zweite Hauptsatz der Thermodynamik besagt, dass thermische Energie nicht in beliebigem Maße in andere Energiearten umwandelbar ist.
Eine alternative Formulierung ist, dass die Entropie, also die Unordnung in abgeschlossenen Systemen bei irreversiblen Prozessen immer zunimmt. Bei reversiblen Prozessen gilt
∆S = 0.
11 Kreisprozesse
Wärmekraftmaschinen sind zyklisch laufende Maschinen, die mechanische Arbeit in Wärme
umwandeln und umgekehrt. Sie werden durch geschlossene Kurven im p-V-Diagramm beschrieben. Diese Kurven werden auch als Kreisprozesse bezeichnet. Zur vereinfachten physikalischen Beschreibung werden diese Kreisprozesse schrittweise in Zustandsänderungen zerlegt.
Abbildung 21: a) Wirkprinzip einer Wärmekraftmaschine bzw. Verbrennungsmotor b) Wirkprinzip einer Kältemaschine bzw. Wärmepumpe
Die Umlaufrichtung des Kreisprozesses ist hier von entscheidender Bedeutung! Die Vorzeichen von Arbeit und Wärme wechseln bei Umkehr der Umlaufrichtung des Kreisprozesses.
Das heißt, dass ein Kreisprozess je nach Umlaufrichtung einen Verbrennungsmotor bzw. Wärmekraftmaschine oder eine Kältemaschine bzw. Wärmepumpe beschreibt.
Eine Wärmekraftmaschine ist ein offenes thermodynamisches System, das kontinuierlich Wärme und Arbeit mit seiner Umgebung austauscht.
11.1 Carnotscher Kreisprozess
Ein Kreisprozess nach Carnot ist aus zwei Isothermen und zwei Adiabaten aufgebaut und
stellt, wenn er im Uhrzeigersinn durchlaufen wird, eine idealisierte Wattsche Dampfmaschine
dar.
Die einzelnen Schritte des Carnot-Zyklus sind wie folgt:
• 1 → 2: isotherme Expansion, Arbeit wird abgegeben, T = const. Wärme muss zugeführt
werden
V2
W12 = −νRT · ln
<0
V1
V2
Q12 = νRT · ln
>0
V1
• 2 → 3: adiabatische Expansion, Arbeit wird abgegeben, kein Wärmeaustausch, Temperatur sinkt
W23 = −CV · ( T2 − T1 ) < 0
Q23 = 0
• 3 → 4: isotherme Kompression, Arbeit wird zugeführt, T = const, Wärme muss abgegeben werden
W34 = −νRT · ln
Q34 = νRT · ln
V4
>0
V3
V4
<0
V3
• 4 → 1: adiabatische Kompression, Arbeit wird zugeführt, kein Wärmeaustausch, Temperatur sinkt
W23 = CV · ( T2 − T1 ) > 0
Q23 = 0
Durch einsetzen in die Adiabatengleichung erhält man das Verhältnis der Volumina.
V
V1
= 4
V2
V3
Als Gesamtarbeit in einem Umlauf des Carnot-Zyklus folgt dann:
∆W = W12 + W23 + W34 + W41
V
V
= −νRT1 · ln 2 − CV · ( T1 − T2 ) + νRT2 · ln 2 + CV · ( T1 − T2 )
V1
V1
V2
= νR ( T1 − T2 ) · ln < 0
V1
Die Gesamtarbeit pro Umlauf ist kleiner als null, d.h. das System verrichtet in jedem Umlauf
Arbeit an seiner Umgebung.
In gleicher Weise kann die Nettowärme in einem Umlauf des Carnot-Zyklus berechnet werden:
∆Q = Q12 + Q23 + Q34 + Q41
V
V
= νRT2 · ln 2 − νRT1 · ln 2
V1
V1
V2
= νR ( T2 − T1 ) · ln > 0
V1
Die Gesamtwärme pro Umlauf ist größe als null, d.h. dem System wird Wärme in jedem
Umlauf zugeführt. Die Summe von Gesamtwärme und Gesamtarbeit ist null. Das System ist
wieder im Ausgangszustand.
11.2 Wirkungsgrad
Der Wirkungsgrad einer Wärmekraftmaschine berechnet sich allgemein über den Quotienten
aus der von der Maschine geleisteten Arbeit |∆W | und der zugeführten Wärme Q12 aus dem
heißen Wärmereservoir zu
(19)
η=
|∆W |
< 1.
Qzu
Für den Carnot-Zyklus lässt sich diese Formel umformen zu
(20)
ηC =
|∆W |
T − T1
= 2
< 1.
Qzu
T2
Nur ein Teil der Wärme von Reservoir T2 kann in mechanische Arbeit umgesetzt werden. Der
Rest erwärmt Reservoir T1 . Der Carnot-Wirkungsgrad ist der höchste theoretisch mögliche
Wirkungsgrad einer Wärmekraftmaschine.
12 Reales Gas
Das reale Gas ist ein erweitertes Modell, das die Eigenschaften von Gasen bei hohen Drücken
und niedrigen Temperaturen besser beschreibt als das ideale Gasmodell. Dies geschieht durch
die Korrektur zweier Annahmen des idealen Gasmodells.
• Die Moleküle haben eine endliche Ausdehnung. Das Volumen muss um das Eigenvolumen der Moleküle korrigiert werden
Vreal = Videal + νb,
wobei b das Eigenvolumen von 1 Mol des Gases ist.
• Es gibt Anziehungskräfte zwischen den Molekülen. Zumeist ist dies die sogenannte vander-Waals Kraft. Diese Anziehungskräfte heben sich im Gas auf. Am Rand des Gases
jedoch existiert eine nach innen gerichtete Kraft vergleichbar mit der Oberflächenspannung von Flüssigkeiten. Diese Kraft reduziert den Druck gemäß
preal = pideal − a · (
ν 2
) ,
V
wobei a · (ν/V )2 als Binnendruck des realen Gases bezeichnet wird.
Die Konstanten a, b sind nur von der Gasart abhängig und können aus den mikroskopischen
Eigenschaften der Wechselwirkung, genauer gesagt dem Potential der anziehenden und abstoßenden Kräfte, hergeleitet werden. Für die Gasgleichung des realen Gases folgt nun
ν2
p + a · 2 · (V − νb) = νRT.
V