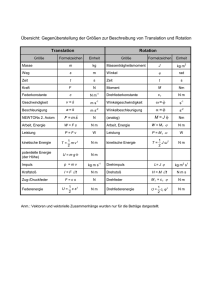
Die „Wahrscheinlichkeitserzeugende Funktion“
Werbung

– 147 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
Die „Wahrscheinlichkeitserzeugende Funktion“
Definition: K sei eine IN 0 – wertige Zufallsvariable .
∞
fK(s) : =
∑ P( K = n ) s
n
= E(sK) , 0 ≤ s ≤ 1,
n =0
heißt „Wahrscheinlichkeitserzeugende Funktion“ (kurz: WEF) von K (bzw. von PK).
Satz: (i) fK(s) ist in [0, 1) unendlich oft differenzierbar.
Für n ∈ IN und die n-te Ableitung f K( n ) (s) gilt:
f K( n ) (1−) : = lim f K( n ) (s) =
s ↑1
∞
∑ P(K = k) ⋅ k ⋅ (k − 1) ⋅ . . . ⋅ (k - n + 1)
=
k=n
= E(K⋅(K – 1)⋅ . . . ⋅(K – n + 1)),
wobei beide Seiten = ∞ sein können.
∞
Speziell: E(K) =
∑ P( K = k ) ⋅ k
= f K′ (1−) ,
k =1
f K′′ (1−) = E(K⋅(K – 1)) ( = E(K2) – E(K), falls E(K) < ∞) ⇒
Var(K) = f K′′ (1−) + f K′ (1−) – (f K′ (1−)) 2 , falls E(K) < ∞ .
(ii) PK ist durch fK(s) eindeutig charakterisiert: P(K = n) =
1 (n)
f K (0) .
n!
(iii) fK(s) ist durch die Angabe von abzählbar vielen Werten fK(si), si ∈ [0, 1], i ∈ IN ,
eindeutig festgelegt. Konvergiert obige Reihe auch für ein s > 1, so ist für jedes n∈ IN
f K( n ) (1−) = f K( n ) (1) < ∞,
und fK(s) ist durch die Angabe von f K( n ) (1) , n∈ IN , eindeutig charakterisiert.
(iv) fK(1) = 1; fK(s) ≥ 0, monoton wachsend und konvex auf [0, 1].
Beweis: Elementare Theorie der Potenzreihen.
Satz:
K1, . . . ,Kn unabhängige IN 0 – wertige Zufallsvariablen . Dann ist
f K1 + . . . + K n (s) = f K1 (s) ⋅. . . ⋅ f K n (s) , 0 ≤ s ≤ 1.
Beweis: f K1 + . . . + K n (s) = E(s K1 + . . . + K n ) = E(s K1 ⋅ . . . ⋅ s K n ) =
= E (s K1 ) ⋅ . . . ⋅ E(s K n ) = f K1 (s) ⋅. . . ⋅ f K n (s) .
– 148 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
Beispiele: (i)
d
K = B(1, p) ⇒ fK(s) = (1 – p) + p⋅s ⇒
d
K = B(n, p) : fK(s) =
n
m=0
d
n
∑ m p
(1 − p) n − m s m = ((1 – p) + p⋅s) n .
m
d
unabhängig. ⇒
K = B(m, p) , L = B(n, p)
d
fK+L(s) = ((1 – p) + p⋅s) m ⋅ ((1 – p) + p⋅s) n = ((1 – p) + p⋅s) m + n ⇒ K + L = B(m + n, p),
bzw.
B(m, p) ∗ B(n, p) = B(m + n, p).
∞
∞
λk k
( λs) k
s = e −λ ∑
k!
k = 0 k!
k =0
(ii) K = Pn(λ) ⇒ fK(s) = e −λ ∑
d
e λ⋅(s-1)⋅ e ρ⋅(s-1) = e (λ+ρ)⋅(s-1)
⇒
= e λ⋅(s-1) , s ∈ [0, 1].
Pn(λ) ∗ Pn(ρ) = Pn(λ + ρ).
E(K) = Var(K) = λ.
d
(iii) K = G(p) ⇒ fK(s) =
∞
∑ p ⋅ (1 - p)
k
⋅ sk =
k =0
f K′ (s) =
Satz:
p
.
1 − (1 − p)s
2 ⋅ p ⋅ (1 − p) 2
p ⋅ (1 − p)
1− p
1− p
′
′
;
f
(
s
)
=
⇒ E(K) =
; Var(K) = 2 .
K
2
3
p
(1 − (1 − p)s)
(1 − (1 − p)s)
p
(Kn)n ∈ IN , K seien IN 0 – wertige Zufallsvariablen. Dann sind äquivalent:
→ P(K = k) für alle k ∈ IN 0 .
(i) P(Kn = k) n
→∞
(ii) P(Kn ∈ A) n
→ P(K ∈ A)
→∞
für alle A ⊂ IN 0 .
→ fK(s) für alle s ∈ [0, 1].
(iii) f K n (s) n
→∞
→ fK(s) für alle s ∈ [0, ε], ε > 0.
(iv) f K n (s) n
→∞
d
(v) Kn n
→ K.
→∞
Anwendung:
Es sei n⋅pn n
→ λ > 0, d.h.
→∞
((1 – pn) + pn⋅s) n = (1 + pn⋅(s – 1)) n = (1 +
⇒
pn =
λ + εn
, εn n
→ 0 . ⇒
→∞
n
λ + εn
→ e λ⋅(s-1) , s ∈ [0, 1].
⋅(s – 1)) n n
→∞
n
d
B(n, pn) n
→ Pn(λ).
→∞
– 149 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
Unabhängige Ereignisse
Satz : Die Ereignisse A und B seien unabhängig. Dann tritt mindestens eines der drei
Ereignisse
A∩B,
A ∆ B ( = (A ∪ B) \ (A ∩ B)) ,
A∩B
(wobei A und B die Gegenereignisse von A und B sind)
mit einer Wahrscheinlichkeit größer oder gleich
4
ein.
9
1, ω ∈ A
Beweis : Es seien X die Indikatorvariable von A, d.h. X(ω) =
, und Y die
0, ω ∉ A
Indikatorvariable von B. Da A und B unabhängig sind, gilt dasselbe für X und Y.
Wir studieren nun f(s), die wahrscheinlichkeitserzeugende Funktion der Variablen (X + Y) :
f(s) := E( s
( X+Y )
) = P(X + Y = 0) + P(X + Y = 1)⋅ s + P(X + Y = 2)⋅s2 =
P( A ∩ B ) + P(A ∆ B)⋅s + P(A ∩ B)⋅s2 =:
a + b⋅s + c⋅s2 , a + b + c = 1
– 150 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
Da
f(s) := E( s X ⋅ s Y ) = E( s X )⋅E( s Y ) =
(P(X = 0) + P(X = 1)⋅ s)⋅ (P(Y = 0) + P(Y = 1)⋅ s),
hat f(s) mindestens eine Nullstelle in den reellen Zahlen, zumindest wenn
c = P(X = 1)⋅ P(Y = 1) > 0.
Dies ist gleichbedeutend mit
2
2
b2
b
b
− ac ≥ 0 ⇔ c − bc − c 2 ≤ ⇔ c ≤ + c ⇔
4
2
2
c ≤
b
+c ⇔
2
b≥
4
9
b
2
c (1 − c) ≤
Wir unterscheiden 3 Fälle :
1.Fall :
c≥
4
9
qed
2.Fall :
c≤
1
9
⇒
3.Fall :
1
4
<c<
9
9
a+b≥
⇔
1
<
3
8
9
⇒
c <
2
3
a ≥
⇒
4
9
b
≥
2
oder
c (1 − c) ≥
qed
2
4
⇒ b≥
9
9
qed,
da min { x ⋅ (1 – x) | d < x < 1 – d } = d ⋅ (1 – d).
Bemerkung : Das folgende Beispiel zeigt, daß die untere Schranke
vergrößert werden kann :
A, B unabhängig mit P(A) = P(B) =
P(A ∩ B) = P(A ∆ B) =
4
;
9
2
3
P( A ∩ B ) =
⇒
1
.
9
4
in obigem Satz nicht
9
– 151 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
Korollar :
Zweimaliger unabhängiger Münzenwurf , jeweiliger Ausgang ∈ { Z, W }.
S sei die Anzahl der in den beiden Würfen gefallenen „Z“.
Es ist unmöglich , die beiden Münzen so zu verfälschen, daß S auf {0, 1, 2} gleichverteilt
ist.
Beweis : Es seien A = „erster Münzenwurf : Z“ und B = „zweiter Münzenwurf : Z“.
A und B sind unabhängig.
(S = 0) = A ∩ B , (S = 1) = A ∆ B , (S = 2) = A ∩ B.
Gleichverteilung ⇒ P( A ∩ B ) = P(A ∆ B) = P(A ∩ B) =
aber :
1
4
< .
3 9
1
,
3
– 152 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion
– 153 –
Kapitel 19: Wahrscheinlichkeitserzeugende Funktion