Musterlösung zur Einsendearbeit: Effizienzsteigernde Ausgaben
Werbung
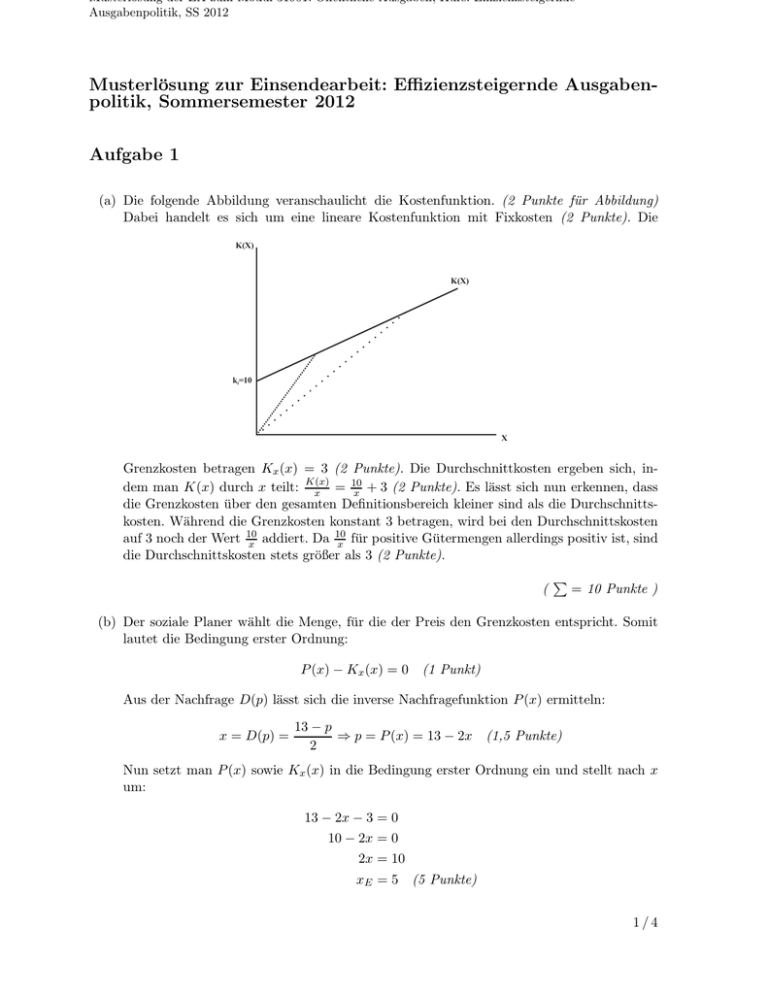
Musterlosung der EA zum Modul 31901: Offentliche Ausgaben, Kurs: Effizienzsteigernde Ausgabenpolitik, SS 2012 Musterlösung zur Einsendearbeit: Effizienzsteigernde Ausgabenpolitik, Sommersemester 2012 Aufgabe 1 (a) Die folgende Abbildung veranschaulicht die Kostenfunktion. (2 Punkte für Abbildung) Dabei handelt es sich um eine lineare Kostenfunktion mit Fixkosten (2 Punkte). Die K(X) K(X) kf=10 X Grenzkosten betragen Kx (x) = 3 (2 Punkte). Die Durchschnittkosten ergeben sich, in10 dem man K(x) durch x teilt: K(x) x = x + 3 (2 Punkte). Es lässt sich nun erkennen, dass die Grenzkosten über den gesamten Definitionsbereich kleiner sind als die Durchschnittskosten. Während die Grenzkosten konstant 3 betragen, wird bei den Durchschnittskosten 10 auf 3 noch der Wert 10 x addiert. Da x für positive Gütermengen allerdings positiv ist, sind die Durchschnittskosten stets größer als 3 (2 Punkte). ( = 10 Punkte ) (b) Der soziale Planer wählt die Menge, für die der Preis den Grenzkosten entspricht. Somit lautet die Bedingung erster Ordnung: P (x) − Kx (x) = 0 (1 Punkt) Aus der Nachfrage D(p) lässt sich die inverse Nachfragefunktion P (x) ermitteln: x = D(p) = 13 − p ⇒ p = P (x) = 13 − 2x 2 (1,5 Punkte) Nun setzt man P (x) sowie Kx (x) in die Bedingung erster Ordnung ein und stellt nach x um: 13 − 2x − 3 = 0 10 − 2x = 0 2x = 10 xE = 5 (5 Punkte) 1/4 Musterlosung der EA zum Modul 31901: Offentliche Ausgaben, Kurs: Effizienzsteigernde Ausgabenpolitik, SS 2012 Die effiziente Menge des Gutes X beträgt 5. Den entsprechenden Preis erhält man durch Einsetzen von xE in die inverse Nachfragefunktion: pE = P (xE = 5) = 13 − 2 · 5 = 3 (5 Punkte) Bei Effizienz beträgt der Güterpreis 3. Die Wohlfahrt ergibt sich im folgenden aus der gesamten Zahlungsbereitschaft abzüglich der Kosten: xE P (x)dx − K(xE ) Ω(xE ) = Z(xE ) − K(xE ) = = [13x − x2 ]x0 E 2 0 − 10 − 3xE = 13 · 5 − 5 − 10 − 3 · 5 = 65 − 25 − 10 − 15 = 15 (7,5 Punkte) Die Wohlfahrt in der effizienten Situation beträgt 15. ( = 20 Punkte ) (c) Der Cournotsche Punkt bezeichnet die Monopollösung. Das Monopolunternehmen maximiert dabei seinen Gewinn π(x) = P (x)x − K(x) = (13 − 2x)x − 10 − 3x = 13x − 2x2 − 10 − 3x = 10x − 2x2 − 10. (1,5 Punkte) Die Bedingung erster Ordnung für das Gewinnmaximum lautet: πx (x) = 10 − 4x = 0 (1,5 Punkte) xM = 4x = 10 10 = 2, 5 = 4 (2,5 Punkte) Setzt man nun xM in die inverse Nachfragefunktion ein, so erhält man den zugehörigen Preis: pM = P (xM = 2, 5) = 13 − 2 · 2, 5 = 13 − 5 = 8 (2,5 Punkte) Somit ergibt sich der Cournotsche Punkt (pM = 8, xM = 2, 5). Die zugehörige Wohlfahrt beträgt: xM P (x)dx − K(xM ) Ω(xM ) = Z(xM ) − K(xM ) = 0 = [13x − x2 ]x0 M − 10 − 3xM = 13 · 2, 5 − 2, 52 − 10 − 3 · 2, 5 = 32, 5 − 6, 25 − 10 − 7, 5 = 8, 75 (5 Punkte) Der Wohlfahrtsverlust zur Effizienzallokation beträgt somit: ΔΩ = Ω(xE ) − Ω(xM ) = 15 − 8, 75 = 6, 25 (2 Punkte) 2/4 Musterlosung der EA zum Modul 31901: Offentliche Ausgaben, Kurs: Effizienzsteigernde Ausgabenpolitik, SS 2012 ( = 15 Punkte ) (d) Um Effizienz im Rahmen einer Preisregulierung herzustellen, würde die Regierung den Grenzkostenpreis setzen und somit p = pE = 3 (2,5 Punkte). Der Gewinn des Unternehmens beträgt in diesem Fall: π(xE = 5) = 10 · 5 − 2 · 52 − 10 = 50 − 50 − 10 = −10 (5 Punkte) Der Unternehmer würde in dem Fall einen Verlust i.H.v. 10 machen. Damit dieser allerdings produziert muss eine Subvention i.H.v. 10 gezahlt werden, um einen Nullgewinn zu erzielen (2,5 Punkte). ( = 10 Punkte ) (e) Die Bedingung erster Ordnung für das second-best-Optimierungsproblem lautet: (1 + λ)[P (x̂) − Kx (x̂)] = −λPx (x̂)x̂ Setzen wir nun die gegebenen Funktionen ein und stellen nach x̂ um, so erhalten wir für λ = 0, 5: (1 + 0, 5)[13 − 2x̂ − 3] = −0, 5 · x̂ · (−2) ⇔1, 5(10 − 2x̂) = x̂ ⇔15 − 3 · x̂ = x̂ ⇔15 = 4x̂ 15 = 3, 75 ⇒x̂0,5 = 4 (5 Punkte) Setzt man diesen Wert in die inverse Nachfragefunktion ein, so erhält man den entsprechenden Preis: p̂0,5 = 13 − 2 · 3, 75 = 13 − 7, 5 = 5, 5 (5 Punkte) Die zu zahlende Subvention entspricht dem Unternehmensgewinn: π̂0,5 = 10 · 3, 75 − 2 · 3, 752 − 10 = 37, 5 − 28, 12 − 10 = −0, 62 Zur Sicherstellung der Produktion ist eine Subvention i.H.v 0,62 fällig (5 Punkte). Die soeben berechneten Größen erhält man für λ = 2 auf analogem Weg: (1 + 2)[13 − 2x̂ − 3] = −2 · x̂ · (−2) ⇔3(10 − 2x̂) = 4x̂ ⇔30 − 6 · x̂ = 4x̂ ⇔30 = 10x̂ ⇒x̂2 = 3 (5 Punkte) Der entsprechende Preis resultiert aus der inversen Nachfrage: p̂2 = 13 − 2 · 3 = 13 − 6 = 7 (5 Punkte) 3/4 Musterlosung der EA zum Modul 31901: Offentliche Ausgaben, Kurs: Effizienzsteigernde Ausgabenpolitik, SS 2012 Die zu zahlende Subvention erhält man wiederum durch Berechnen des Unternehmensgewinnes: π̂2 = 10 · 3 − 2 · 32 − 10 = 30 − 18 − 10 = 2 Hier resultiert ein positiver Unternehmensgewinn. Daher sind keine Subventionen erforderlich (5 Punkte). Interpretation bezüglich λ: Der Parameter λ stellt den Schattenpreis des öffentlichen Geldes dar. Je höher λ ist, desto höher ist der Effizienzverlust bei Finanzierung der Subvention. In den obigen Rechnungen zeigt sich nun, dass das höhere λ auch zu einer geringeren Menge sowie einem höheren Preis des öffentlichen Gutes führt. Bei λ = 0, 5 wird noch eine Subvention gezahlt, während dies bei λ = 2 nicht mehr der Fall ist. Dies bedeutet, dass eine Subvention ßu teuerı̈st. Die Effizienzverluste zur Finanzierung der Subvention sind zu groß. (5 Punkte) ( = 35 Punkte ) (e) Die Preiselastizität der Nachfrage für λ = 0, 5 ergibt: P (x̂0,5 ) x̂0,5 Px (x̂0,5 ) 13 − 2x̂0,5 =− x̂0,5 · (−2) 13 − 2 · 3, 75 =− 3, 75 · (−2) 5, 5 = 0, 73 =− −7, 5 0,5 = − (5 Punkte) Dies bedeutet, dass sich die Nachfrage um 0,73 % verringert wenn sich der Preis um 1 % erhöht. (Obwohl die errechnete Elastizität positiv ist, ist die Nachfragewirkung einer Preisänderung negativ. Das positive Vorzeichen ergibt sich aus dem Minus vor dem Bruch in .) (5 Punkte). ( = 10 Punkte ) 4/4











