Möglichkeiten der Energiegewinnung mit Hilfe des Piezo

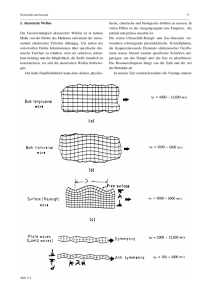
Möglichkeiten der Energiegewinnung mit Hilfe
des Piezo-Effekts
~ Eine Besondere Lernleistung (BLL) von Nico Lüdtke ~
Gymnasium im Paul-von-Denis-Schulzentrum Schifferstadt
Neustückweg 12
67105 Schifferstadt
Referenzfach:
Physik
Betreuender Lehrer:
Hr. Heidinger
Abgabedatum:
15.07.2014
~1~
Inhalt
3
• 1. Der Piezo-Effekt
◦ 1.1 Definition
3
◦ 1.2 Geschichte und Überblick über Anwendungen
3
◦ 1.3 Eigenschaften piezoelektrischer Materialien
4
◦ 1.4 Erklärung des Piezo-Effekts
5
▪ 1.4.1 Der direkte longitudinale piezoelektrische Effekt
5
▪ 1.4.2 Der direkte transversale piezoelektrische Effekt
6
▪ 1.4.3 Der longitudinale und transversale reziproke piezoelektrische Effekt
6
▪ 1.4.4 Weitere Piezo-Effekte
6
◦ 1.5 Abhängigkeit von den Abmessungen des Kristalls
7
◦ 1.6 Seignettesalzkristalle
9
◦ 1.7 Piezoelektrische Keramiken
10
◦ 1.8 PZT in Feuerzeugen
13
• 2. Nutzung als Generator
14
◦ 2.1 Idee
14
◦ 2.2 Aktuelle Einsatzgebiete
14
◦ 2.3 Energie gewinnen oder stehlen?
15
◦ 2.4 Versuche
15
▪ 2.4.1 Der Schallwandler
15
▪ 2.4.2 Verhalten bei Druckänderung
15
▪ 2.4.3 Stapeln von Schallwandlern
18
▪ 2.4.4 Messen der Energie
19
▪ 2.4.5 Energiegewinnung am Fahrrad
20
▪ 2.4.6 Schallwandler in Schuhen
24
24
◦ 2.5 Fazit
~2~
1. Der Piezo-Effekt
1.1 Definition 1,2
Bei bestimmten Kristallen tritt bei Einwirkung einer äußeren Kraft bzw. mechanischen Drucks auf
den Kristall eine Ladungsverschiebung im Kristall (Polarisierung) auf. Dieses Phänomen wird als
Piezo-Effekt bezeichnet. Neben dem soeben angedeuteten direkten piezoelektrischen Effekt
besitzen diese Kristalle auch die Eigenschaft, sich bei Anlegen einer äußeren Spannung zu
deformieren. Dieser reziproke beziehungsweise inverse piezoelektrische Effekt tritt bei den gleichen
Kristallen wie der direkte piezoelektrische Effekt auf und kann als dessen Umkehrung betrachtet
werden. Die Bezeichnung Piezo-Effekt leitet sich vom griechischen Verb piezein (πιέζει) ab,
welches (zusammen-)drücken oder pressen bedeutet.
1.2 Geschichte und Überblick über Anwendungen 1,2,3,4
Bereits 1880 wurde der direkte piezoelektrische Effekt des Stoffes Turmalin von Jaques und Pierre
Curie beschrieben. Kurze Zeit später entdeckten sie auch den reziproken piezoelektrischen Effekt
und piezoelektrische Eigenschaften anderer Kristalle. Neben Turmalin gehören Quarz und
Seignette- bzw. Rochellesalz zu den wichtigsten piezoelektrischen Kristallen. Aufgrund der
Instabilität des Seignettesalzes wird in der Technik hauptsächlich Quarz verwendet, obwohl der
Piezo-Effekt bei Seignettesalz deutlich stärker ist. α-Quarz fand zunächst Anwendung in
Ultraschallwandlern und als Schwingquarze zur Frequenzstabilisierung, z.B. in Uhren. In den
letzten Jahrzehnten, vor allem seit den 1960er Jahren, übernahmen piezoelektrische Keramiken
menschlichen Ursprungs immer mehr die Funktionen, die zuvor von natürlichen Kristallen erfüllt
worden waren. Da diese polykristallinen Keramiken größere elektrische Spannungen induzieren
(direkter Piezo-Effekt) beziehungsweise größere Auslenkungen zeigen (inverser Piezo-Effekt) und
deutlich besser bezüglich Form und Eigenschaften auf den Einsatzbereich abgestimmt produziert
werden können, werden sie z.B. in Aktoren zur Präzisionspositionierung und als Abstands-,
(Ultra-)Schall- oder Drucksensoren verwendet. Außerdem können piezoelektrische Keramiken
relativ kostengünstig hergestellt werden. Deshalb finden vor allem Blei-Zirkonat-Titanate (PZT)
breite Anwendung in Feuerzeug- und Grillanzündern oder in einfachen Lautsprechern.
~3~
1.3 Eigenschaften piezoelektrischer Materialien 1,5,6
Um piezoelektrische Eigenschaften aufzuweisen, müssen Kristalle und Keramiken bestimmte
Bedingungen erfüllen.
So können nur Stoffe mit mindestens einer polaren Achse ladungsverschiebend auf mechanischen
Druck reagieren. Polare Achsen sind Achsen, bei denen die beiden Enden nicht beliebig
vertauschbar sind; „Eine 180°-Drehung um eine zur polaren Achse senkrechte Achse bringt den
betreffenden Kristall nicht mit der Ausgangsstellung zur Deckung.“ 1 (Besitzt ein Stoff exakt eine
polare Achse, so weist er zusätzlich auch pyroelektrische Eigenschaften auf, d.h. wird durch
Temperaturänderung polarisiert.) Der Kristall bzw. die Elementarzelle des Kristalls darf also kein
Symmetriezentrum besitzen, da die Existenz eines solchen Zentrums polare Achsen ausschließt.
Außerdem dürfen sich die einzelnen Ladungsverschiebungen nicht durch unterschiedliche
Richtungen der Ladungsverschiebung beziehungsweise Raumorientierungen der Struktureinheiten
ausgleichen. Dieses Problem kann bei Kristallen durch Verzwillingung auftreten. Bei Keramiken
sind die Domänen vor der Polung immer statistisch verteilt. Daher kann der Piezo-Effekt nur bei
gepolten Keramiken gemessen und genutzt werden. (Der Polungsprozess wird später bei der
Erklärung des Piezo-Effekts bei Keramiken beschrieben.)
Piezoelektrische Kristalle und Keramiken sind immer nichtleitend, da ansonsten die entstehende
Spannung sofort wieder ausgeglichen würde.
Tiefquarz beziehungsweise α-Quarz, also reine Quarzkristalle bei einer Temperatur von weniger als
573° (bei einem Druck von 1 bar), erfüllen diese Anforderungen.
In den folgenden Skizzen werden je zwei Sauerstoffionen, und damit vier negative
Einheitsladungen, zu einem blauen Kreis zusammengefasst. Jedes vierfach positiv geladene
Siliciumion wird durch einen roten Kreis dargestellt. Die blauen bzw. roten Ringe kennzeichnen
jeweils die Ladungsschwerpunkte der negativen bzw. positiven Ladungen, die entscheidend für die
Spannung sind. (Die Atome werden der Einfachheit halber als Ionen bezeichnet, obwohl die Si-OBindungen kovalente Anteile haben.)
Si4+-Ion
Positiver Ladungsschwerpunkt
2 O2--Ionen
Negativer Ladungsschwerpunkt
~4~
Im Quarzkristall können Sechsecke aus je sechs
Sauerstoffwerden.
und
drei
Abbildung
Silicium-Atomen
1
skizziert
eine
gefunden
solche
Strukturzelle.
Die drei polaren Achsen X1, X2 und X3 sind durch
durchgängige, die drei neutralen Achsen Y1, Y2 und Y3
durch gestrichelte Linien gekennzeichnet. Die optische
Achse ragt senkrecht aus der Zeichenebene heraus.
1.4 Erklärung des Piezo-Effekts 1,5,6,7
Der
Piezo-Effekt
lässt
sich
am
Beispiel
der
Abbildung 1.3.a
Elementarzelle des Quarz erklären:
1.4.1 Der direkte longitudinale piezoelektrische Effekt
Um im Folgenden die einzelnen Atome beschreiben zu
können, wird die Benennung nach Abbildung 1 verwendet.
O1,2
Wird eine äußere Kraft auf diese Strukturzelle in der in
Abbildung 2 angedeuteten Richtung ausgeübt, so führt das zu
einer
Deformation:
Das obere SiliciumAtom Si1 wird nach
O3,4
unten,
die
unteren
Sauerstoff-Atome O3,4
nach oben gedrückt.
Abbildung 1.4.a
Dadurch verschieben sich der positive und der negative
Ladungsschwerpunkt und liegen nicht mehr an der gleichen
Stelle. Es entsteht also eine Spannung, die in Abbildung 2
durch die rote bzw. blaue Farbe der Flächen angedeutet
wird. Die Lagen der Ladungsschwerpunkte werden, wie
durch die gestrichelten Linien angedeutet, durch die
Schnittpunkte der Seitenhalbierenden in den gedachten
Abbildung 1.4.b
Dreiecken aus den positiven bzw. negativen Ladungen ermittelt.
Diese Komprimierung in vertikaler Richtung geht einher mit einer horizontalen Dilatation.
Eine Komprimierung entlang einer der anderen beiden polaren Achsen hätte natürlich die gleichen
Folgen, da die Skizze um 120° gedreht wieder sich selbst abbildet.
~5~
Je stärker die Kraft auf den Kristall ist, desto stärker wird dieser deformiert, desto stärker werden
die Ladungen im Kristall verschoben und desto größer ist demnach die erzeugte Spannung.
Eine Dilatation in vertikaler Richtung kann als negative Kraft auf die Strukturzelle interpretiert
werden, sorgt für eine Verschiebung der Atome in die jeweils entgegengesetzten Richtung und führt
daher zu einer Spannung umgekehrten Vorzeichens.
1.4.2 Der direkte transversale piezoelektrische Effekt
Wird auf den Quarz eine Kraft in der in
Abbildung 3 skizzierten Richtung ausgeübt,
dann wird der Quarz ähnlich einer Dilatation
in vertikaler Richtung deformiert. Während
die Atome rechts und links (O 1,2,O5,6,Si2,Si3)
in die Mitte gedrückt werden, verschieben
sich das obere Silicium-Ion Si1 und die
unteren Sauerstoff-Ionen O3,4 nach außen.
Das führt auch hier zu einer Verschiebung
der Ladungsschwerpunkte und somit zu einer
Spannung, deren Vorzeichen umgekehrt zu
dem
der
Spannung
beim
vertikalen
Abbildung 1.4.c
Komprimieren ist.
Auch beim transversalen piezoelektrischen Effekt steigt die Spannung mit zunehmender Kraft auf
den Kristall an und eine Dilatation anstelle der Kompression ändert das Vorzeichen der Spannung.
1.4.3 Der longitudinale und transversale reziproke piezoelektrische Effekt
Wie bereits in der Einleitung angedeutet, führt das Anlegen einer Spannung an einen Quarzkristall
zu einer Deformation dieses Kristalls.
Der longitudinale reziproke piezoelektrische Effekt beschreibt das Ausdehnen des Kristalls in
Richtung einer polaren Achse bei Anlegen einer Spannung entlang einer nicht-polaren Achse.
Der transversale reziproke piezoelektrische Effekt ist die Ausdehnung eines Kristalls in Richtung
einer nicht-polaren Achse beim Anlegen einer Spannung entlang einer polaren Achse.
1.4.4 Weitere Piezo-Effekte
Auch Deformationen anderer Art führen zu Spannungen. So reagieren piezoelektrische Kristalle
z.B. auch auf Verdrillung ladungsverschiebend, piezoelektrische Schereffekte existieren ebenfalls.
~6~
1.5 Abhängigkeit von den Abmessungen des Kristalls 2,6
Die erzeugte Ladungsmenge ist neben der Kraft auf den Kristall und dem Stoff des Kristalls auch
abhängig von den Abmessungen des Kristalls. Dies soll im Folgenden am Beispiel des Tiefquarz
erläutert werden:
Für jeden piezoelektrischen Kristall geben sog. Piezoelektrische Ladungskoeffizienten d an, wie
viel Ladung pro Kraft abgeschieden wird. Indizes geben an, in welche Richtung die Kraft und die
erzeugte Spannung wirken. Der erste Index steht für die Richtung der mechanischen Kraft, der
zweite für die Ladungsverschiebung. Sind beide Indizes gleich (11), so ist also der longitudinale
Piezo-Effekt gemeint, sind beide verschieden (12), so wird die Ladung senkrecht zur Richtung der
Kraft verschoben (transversaler Piezo-Effekt). Für Schereffekte gibt es noch weitere
Indexkombinationen. d wird in der Einheit Coulomb pro Newton angegeben. Für Quarz gilt:
d11=d12.
Die Ladung Q ist proportional zur Kraft F auf den Kristall: Q~F. (experimentelle Bestätigung:
2.4.2)
Die Auswirkungen von Höhe beziehungsweise Breite des Kristalls auf die Ladung hängen von der
Art des Effekts ab:
Beim longitudinalen Effekt sorgt eine größere Fläche bei gleich bleibendem Druck dafür, dass an
mehr Stellen nebeneinander die gleiche Ladungsmenge, insgesamt also mehr Ladung an den
Flächen bemerkbar wird. Gleichzeitig führt die größere Fläche allerdings auch für ein Aufteilen der
Kraft und nach
geringeren
Druck.
p=
F
A
Da
für einen
die
Fläche
zugleich proportional zur Ladung pro
Druck und antiproportional zum Druck
ist, ist die Ladung unabhängig von ihr.
Abbildung 1.5.a
Auch die Dicke des Kristalls hat
keinerlei Auswirkungen auf die erzeugte Ladung. Eine größere Dicke verringert zwar den Druck auf
jede
einzelne
Strukturzelle
nicht,
vergrößert aber auch die Ladung pro
Druck nicht.
Für den longitudinalen Piezo-Effekt
gilt also:
Q=d 11⋅F .
Abbildung 1.5.b
~7~
Beim transversalen Effekt sind Druck pro Kraft und Ladung pro Druck nicht von der selben Fläche
abhängig:
Je größer die Fläche A1, auf die die Kraft wirkt, desto stärker verteilt sich
die Kraft, desto kleiner wird also der Druck. Es gilt also nach
auch p∼
p=
F
A
1
1
. Da Q ~ p gilt also auch Q∼
.
A1
A1
Je größer die Fläche A2, an der die Ladung auftritt, desto größer die
Ladung Q bei gleichem Druck p: Q∼ A2 . Der Druck ist unabhängig
von dieser Fläche.
Abbildung 1.5.c
Es fällt auf, dass die Breite b des Kristalls jeweils ein Faktor zur
Abbildung 1.5.d
Berechnung von A1 und A2 ist. Da Q proportional von A2 und antiproportional von A1 abhängt,
spielt b keine Rolle für die Ladung. Für die Berechnung der Ladung sind also neben d 12 und F nur
noch l und d von Bedeutung und ersetzen A2 beziehungsweise A1. Für den transversalen PiezoEffekt gilt also:
A2 =b⋅l
d
A1
A1=b⋅d
A3=d⋅l
b
X (polare Achse)
l
d
y (neutrale Achse)
(o
pt
.
Ac
hs
e)
l
z
Q=d 12⋅F
Abbildung 1.5.e
~8~
1.6 Seignettesalzkristalle 6,8,9,10
Seignettesalz oder auch Rochellesalz ist ein Salz der Weinsäure mit der chemischen
Verhältnisformel KNaC4H4O6 · 2H2O. Seignettesalzkristalle weisen ein Ionengitter aus K +-Ionen,
Na+-Ionen und C4H4O62--Ionen auf.
Ein solcher Kristall kann durch eine Reaktion von Kaliumhydrogentartrat (Weinstein) und
Natriumcarbonat (Waschsoda) erzeugt werden.
Dazu wird zunächst Kaliumhydrogentartrat in Wasser gelöst und dann auf ca. 80 °C erhitzt. In die
Lösung wird Natriumcarbonat gegeben. Dabei entsteht Kohlensäure. Wenn bei Zugabe von
Natriumcarbonat keine Kohlensäure mehr entsteht, ist die Reaktion fertig. Die entstandene
Flüssigkeit wird anschließend mehrere Tage bei Raumtemperatur gelagert. Dabei bilden sich
Kristalle.
Es handelt sich dabei um eine Säure-Base-Reaktion, bei der Kaliumhydrogentartrat Protonen an
Natriumcarbonat abgibt:
Abbildung 1.6.a
~9~
Die so erhaltenen Kristalle weisen piezoelektrische Eigenschaften auf. Diese können mit einem
Oszilloskop nachgewiesen werden. Werden zwei Elektroden am Kristall angebracht, können bei
Schlägen auf den Kristall Spannungen nachgewiesen werden.
Die hergestellten Kristalle sind jedoch keine perfekten Einkristalle, weshalb es im Kristall Teile mit
unterschiedlicher Polarisation gibt. Damit löschen sich die piezoelektrischen Effekte teilweise
wieder aus. Eine quantitative Messung mit diesen Kristallen wird außerdem durch die Instabilität
und begrenzte Größe der Kristalle erschwert.
1.7 Piezoelektrische Keramiken 2,3,4,11
Das für einfache Anwendungen wichtigste piezoelektrische Keramikmaterial ist Bleizirkonattitanat,
kurz PZT.
Die Verhältnisformel des PZT lautet Pb(Zr xT(1-x))O3, wobei x für Werte zwischen 0 und 1 steht:
0≤x≤1.
Oberhalb der Curietemperatur von je nach Titananteil, also je nach x in der Verhältnisformel,
zwischen 230 und 500 °C besitzen die Elementarzellen der einzelnen PZT-Kristalle eine kubische
Form, wobei die Pb2+-Ionen die Ecken bilden, die O2--Ionen kubisch-flächenzentriert und die Zr4+bzw. Ti4+-Ionen kubisch-raumzentriert angeordnet sind. Oberhalb der Curietemperatur weist PZT
also keine piezoelektrischen Eigenschaften auf:
Pb2+
O2Zr4+ bzw. Ti4+
Abbildung 1.7.a
Unterhalb der Curietemperatue jedoch tritt eine spontane Polarisation auf. Die Zr 4+- bzw. Ti4+-Ionen
befinden sich nicht mehr exakt im Zentrum der Elementarzelle, sodass diese Dipolcharakter
annimmt. Unterhalb der Curietemperatur besitzt PZT polare Achsen und zeigt Piezo-Effekte. Diese
Kristallstruktur des Verhältnisses ABO3 wird nach dem Stoff Perowskit (CaTiO3) als PerowskitKristallstruktur bezeichnet.
~ 10 ~
Dass die Verhältnisformel Pb(ZrxT(1-x))O3 ist, obwohl in einer Elementarzelle acht Pb 2+-Ionen, sechs
O2--Ionen und ein Zr4+- bzw. Ti4+-Ion enthalten sind, liegt an der Verknüpfung der Elementarzellen
zu einem Kristall:
Da die Pb2+-Ionen die Elementarzellen über Ecken verknüpfen, gehört jedes Pb 2+-Ion gleichzeitig
zu acht Elementarzellen. Sauerstoffionen dagegen verbinden immer nur zwei Elementarzellen,
während Zirkonium- bzw. Titaniumionen immer nur einer Elementarzelle angehören.
1
5
2
6
3
7
4
8
1
2
Abbildung 1.7.b
Um auf die Verhältnisformel zu kommen, teilt man daher die Anzahl eines Atoms pro
Elementarzelle durch die Anzahl Elementarzellen, denen es angehört:
8
1
6
n Pb= =1 ; n Zr +nTi= =1 ; n O= =3
8
1
2
Die Dipole bilden Bereiche mit einheitlicher Ausrichtung, sogenannte Domänen.
Innerhalb dieser Domänen ist der Stoff also in eine Richtung polarisiert, d.h. alle Zr 4+- bzw. Ti4+Ionen sind in die gleiche Richtung aus den Zentren der Elementarzellen verschoben. Die
verschiedenen Domänen weisen jedoch unterschiedliche Polarisationsrichtungen auf. Da die
Domänen sehr klein sind , sind bereits in kleinen Keramikstücken sehr viele Domänen enthalten. Da
zunächst jede Domäne zufällig polarisiert ist und sehr viele Domänen existieren, gilt das „Gesetz
der großen Zahlen“ aus der Mathematik: Die Domänen innerhalb der polykristallinen Keramik sind
statistisch verteilt, sodass die Keramik makroskopisch betrachtet kein Dipol ist. Wie bereits im
Kapitel „Eigenschaften piezoelektrischer Materialien“ beschrieben, heben sich die Piezo-Effekte
der einzelnen Domänen bzw. Kristallite gegenseitig auf, sodass kein mess- bzw. nutzbarer PiezoEffekt existiert.
~ 11 ~
Piezoelektrische Keramiken werden daher gepolt. Dazu werden sie in ein starkes elektrisches Feld
gebracht. Dabei vergrößern sich die Domänen mit Polarisation in gleicher oder ähnlicher Richtung
wie das Feld, anders polarisierte Domänen werden verdrängt, bis zur Sättigungspolarisation P S.
Wird das Feld wieder entfernt, bleibt ein Teil der Polarisation erhalten (Remanenz P R). Wird
anschließend ein elektrisches Feld in entgegengesetzter Richtung und dann wieder ein Feld in der
Richtung des ersten Feldes angelegt, ergibt sich eine typische Hysteresekurve (skizzenhafte
Darstellung ohne Messwerte):
Abbildung 1.7.c
Modellhafte Vorstellung der Polung (Pfeile deuten die Polarisation der Domänen an):
Vor der Polung
Sättigungspolarisation
PS
Remanente
Polarisation PR
Abbildung 1.7.d
~ 12 ~
1.8 PZT in Feuerzeugen 6,16,17
In Feuerzeugen sorgen oft PZT-Elemente für einen Funken, der das Gas dann entzündet.
Dabei wird beim Drücken eine Feder gespannt, die dann einen kleinen Hammer mit hoher
Geschwindigkeit auf das piezoelektrische Bauteil drückt. Durch die kurzzeitig hohe Kraft entsteht
eine sehr große Spannung, die für einen kleinen Blitz ausreicht. Mit dem Drücken der
Betätigungstaste wird gleichzeitig auch das Ventil am Tank geöffnet, sodass Gas ausströmt, welches
durch den Blitz entzündet wird:
Abbildung 1.8.a
Betätigungstaste, Hammer und Piezoelement können aus solchen Feuerzeugen ausgebaut werden.
Mit diesen Teilen lassen sich sichtbare Blitze erzeugen. Das Ende des Kabels wird in sehr kleiner
Distanz zu einer Erdung gehalten und die Taste betätigt. Ein solcher Entladungsfunke überwindet
eine Strecke von 3 bis 4 mm, die Spannung beträgt also kurzzeitig ungefähr 10000 V.
~ 13 ~
2. Nutzung als Generator
2.1 Idee
Obwohl es naheliegend klingt, einen Effekt, der mechanische in elektrische Energie umwandelt,
zum Generieren elektrischen Stroms zu nutzen, wird der Piezo-Effekt derzeit kaum zur
Stromgewinnung eingesetzt.
In Zeiten des Klimawandels und des Ablehnens von Atomkraftwerken wird aktuell in Deutschland
im Rahmen der angestrebten Energiewende nach neuen Quellen erneuerbarer Energie gesucht.
In vielen Bereichen des Alltags könnte durch Ausnutzen ansonsten in Reibungswärme
beziehungsweise Verformungsenergie umgewandelter und damit verpuffender Energie elektrische
Energie generiert werden. Generatoren sind per Definition Maschinen, die mechanische in
elektrische Energie umwandeln. Dieses Nutzen von in der Regel geringen Mengen Energie aus der
Umgebung wird als Energy Harvesting bezeichnet.
Dass der direkte Piezo-Effekt derzeit fast ausschließlich für Sensorik genutzt wird, liegt an der
Ineffizienz beziehungsweise dem relativ geringen Wirkungsgrad.
Dennoch wird aktuell an den Möglichkeiten der Nutzung des piezoelektrischen Effekts zur
Energiegewinnung geforscht und in seltenen Fällen werden Piezokeramiken sogar schon als
Generatoren genutzt:
2.2 Aktuelle Einsatzgebiete 12,13,14,15
Wenn überhaupt piezoelektrische Bauteile als Generator genutzt werden, dann meist in kleinem
Maßstab. So hat die Firma „EnOcean“ einen Schalter entwickelt, in dem ein Piezo-Generator in die
Taste integriert ist. Die durch den Tastendruck erzeugte elektrische Energie wird dabei zum
Aussenden von Funksignalen genutzt. Solche energieautarken Schalter, in denen Piezo-Elemente
gleichzeitig als Sensor und Generator genutzt werden, kommen ohne Batterien aus und sind somit
weniger wartungsaufwändig.
Das israelische Unternehmen „Innowattech“ hingegen nutzt bereits heutzutage den Piezo-Effekt,
indem es speziell dafür entwickelte Piezoelemente in Autobahnen wenige Zentimeter unter der
Asphaltoberfläche beziehungsweise in Schienen für Züge, sowie Untergrund- und Straßenbahnen
einbaut, um damit elektrische Energie zu generieren und gleichzeitig falls erwünscht Daten über die
Nutzung der Straßen wie zum Beispiel über Anzahl und Geschwindigkeit der Autos zu sammeln.
Nach Angaben der Online-Fachzeitschrift Green Prophet können so auf stark befahrenen
Autobahnen ca. 500 kW pro Kilometer erzeugt werden. Ein so großflächiger Einsatz ist jedoch
aktuell die Ausnahme.
~ 14 ~
2.3 Energie gewinnen oder stehlen? 2,15
Spontan kommen oft Zweifel auf, ob solche Autobahnen tatsächlich Energie gewinnen und nicht als
„Schmarotzer“ den Verbrauch der Fahrzeuge erhöhen und somit weniger umweltfreundlich sind.
Innowattech jedoch erklärt, dass die Energie ausschließlich die ansonsten ungenutzte Wärme, die
bei der Verformung entsteht, verringert werde. Da der Young's Modulus, ein Maß für die
F
)
A
P
Y=
=
, größer als der von Asphalt und die
Δl
Δl
( ) ( )
l
l
(
Verformbarkeit mit der Formel
Verformbarkeit damit kleiner als die von Asphalt seien, sinke die vertikale Gesamtverformung der
Straße und die Fahrzeuge müssten nicht mehr Energie aufwenden.
2.4 Versuche
2.4.1 Der Schallwandler
Ziel der folgenden Versuche ist es, Anwendungsmöglichkeiten aufzuzeigen, um mit möglichst
einfachen, kostengünstigen Mitteln möglichst viel elektrische Energie ohne Aufwandssteigerung
aus alltäglichen Situationen mit Hilfe des Piezo-Effekts zu gewinnen.
Aufgrund der geringen Anschaffungskosten werden für alle folgenden Experimente PiezoSchallwandler benutzt. Diese bestehen aus einer runden Metallscheibe, auf der eine dünne
(senkrecht zur Ebene der Metallscheibe gepolte) Piezokeramikschicht aufgebracht ist.
Normalerweise werden Schallwandler als einfache Lautsprecher genutzt, da die Piezokeramik bei
Anlegen einer Spannung sich und die Metallscheibe verformt (inverser piezoelektrischer Effekt).
Bei Anlegen einer Wechselspannung schwingt der Schallwandler also in der Frequenz der
Spannung.
Wie bei allen Piezokeramiken existiert aber auch hier ein direkter piezoelektrischer Effekt.
2.4.2 Verhalten bei Druckänderung
Zunächst wird getestet, wie sich solche Schallwandler verhalten, wenn sie mechanischem Druck
ausgesetzt werden. Dabei soll experimentell bestätigt werden, dass U~F und damit nach Q=c⋅U
auch wie in 1.5 behauptet Q~F gelten.
Dazu wird der Druck auf einen zuvor entladenen Schallwandler durch Aufbringen einer bestimmten
Masse auf den Schallwandler erhöht. Dann wird die erzeugte Spannung gemessen. Dieser Versuch
wird mit verschiedenen Massen wiederholt.
~ 15 ~
Abbidung 2.4.a
Der Versuch wird also nach den folgenden Schritten durchgeführt:
•
Der Versuch wird wie in der Skizze beschrieben, aber vorerst ohne Massestücke, aufgebaut.
•
Der Schallwandler wird kurzgeschlossen und damit entladen.
•
Der Schalter ist offen bzw. die Verbindung getrennt.
•
Ein Massestück wird auf das Holzgestell gestellt.
•
Der Schalter wird wieder geschlossen bzw. die Verbindung wieder hergestellt.
•
Die Spannung wird am Voltmeter bzw. Oszilloskop abgelesen.
•
Das Massestück wird wieder entfernt und die Schritte 2 bis 6 werden mehrfach mit
verschiedenen Massen wiederholt.
~ 16 ~
Es ergeben sich dabei folgende Werte:
U
2,5
5
10
14
17
22
24
26
31
[V]
m
50
100 200 300 400 500 600 700 1000
[g]
Eine Proportionalität zwischen Masse und Spannung ist deutlich erkennbar. Diese gilt jedoch nur
bis zu einer Masse von ca. 300 g, danach nimmt die Steigung der Spannung immer weiter ab und
die Energieumwandlung ist weniger effizient.
Abbildung 2.4.b
Für Anwendungen, bei denen große Kräfte und Drücke auf den Piezo-Generator wirken, sind
Schallwandler also eher ungeeignet.
Da die Kraft durch F =9,81 N /kg⋅m definiert und somit proportional zur Masse m ist, ist auch
die Kraft proportional zur Spannung. Die Fläche ist während der gesamten Versuchsreihe gleich,
sodass der Druck hier auch proportional zur Spannung ist.
Abbildung 2.4.c
~ 17 ~
2.4.3 Stapeln von Schallwandlern
Der Piezo-Generator verformt sich dabei nur wenig, fast die komplette Kraft wirkt weiter auf die
Tischplatte.
Um mehr elektrische Energie zu generieren, können daher mehrere Piezo-Generatoren gestapelt
werden.
Werden zwei gestapelte Schallwandler elektrisch in Reihe geschaltet, addieren sich die Spannungen
der beiden Generatoren. Wird der selbe Aufbau wie in 4.2.2 verwendet, werden folgende Werte
gemessen:
U
5
9
20
27
39
45
[V]
m
50
100
200
300
400
500
[g]
Wie erwartet, werden etwa doppelt so hohe Spannungen gemessen. Dass weniger Effizienzverlust
erkennbar ist, liegt lediglich daran, dass nur Massen bis 500g verwendet wurden.
Abbildung 2.4.d
Abbildung 2.4.e
Abbildung 2.4.f
~ 18 ~
2.4.4 Messen der Energie
Um die Energie beim Hinzufügen eines 200g-Stücks zum in 2.4.2 geschilderten Versuch zu messen,
wird der Spannungsverlauf beim Entladen über einen Widerstand R=1kΩ des Schallwandlers mit
Hilfe eines Speicheroszilloskops gesichert und betrachtet:
Abbildung 2.4.g
Bleiben Strom und Spannung konstant, dann ist die Energie W el =U⋅I⋅t .
Da sich Stromstärke I und Spannung U jedoch während des betrachteten Zeitintervalls deutlich
0,023
ändern, muss das Integral über die Zeit gebildet werden: W el = ∫ U ( t)⋅I ( t)⋅dt .
t =0
Zu jedem Zeitpunkt gilt
I ( t)=
U (t)
.
R
0,023
In die Formel eingesetzt beträgt die Energie also W el = ∫
t =0
U (t ) 2
⋅dt .
R
Die Spannungen wurden in den Zeitintervallen dt=0,001s gemessen.
2
2
2
2
Daraus ergibt sich: W el =U (0) ⋅U (0,001) ⋅U (0,002) ⋅...⋅U (0,023) ⋅
dt
R
2
2
2
2 0,001 s
W el =U (0) ⋅U (0,001) ⋅U (0,002) ⋅...⋅U (0,023) ⋅
1kΩ
Setzt man die Werte für U(t) ein, so erhält man das Ergebnis W el ≈0,00023 Js
Die Energie entspricht also der durch den
Widerstand R geteilten Fläche unter dem Quadrat
der Spannung.
Abbildung 2.4.h
~ 19 ~
2.4.5 Energiegewinnung am Fahrrad
Ziel des folgenden Versuchs ist es, beim Radfahren Kondensatoren zu laden.
Wie bei der in 2.2 beschriebenen Anwendung in Autobahnen sollen Druck und Vibration beim
Fahren genutzt werden. Hier werden die Piezo-Generatoren jedoch am Reifen und nicht in der
Fahrbahn angebracht. Das hat den Vorteil, dass beim Fahren immer wieder der selbe Schallwandler
den Boden berührt und elektrische Energie generiert, während man ansonsten immer wieder über
die gleiche Stelle fahren oder eine große Fläche mit Schallwandlern ausstatten müsste.
Die Kondensatoren, die über verschiedene Diodenschaltungen geladen werden, sind über einen
Klebebandstreifen an den Speichen befestigt. Die Kabel werden durch ein Loch in der Felge innen
geleitet, um eine Behinderung beim Drehen durch die Bremsen zu vermeiden:
Federgabel
Bremse
Schallwandler
Kabel
Schaltung
(Kondensator,
Dioden)
Reifen
Felge
Speiche
Abbildung 2.4.i
Mit diesem Aufbau sollen Kondensatoren geladen werden. Dabei werden verschiedene Schaltungen
verwendet und die Kapazität des Kondensators, sowie die Kraft auf den Reifen werden variiert.
~ 20 ~
Verschiedene Schaltungen:
Die Abbildungen 2.4.f bis 2.4.i zeigen die an
einem Kondensator mit der Kapazität c=220μF
erzeugte Spannung und Energie beim Fahren des
Fahrrads relativ zur gefahrenen Strecke.
Bei allen drei verwendeten Schaltungen steigt die
Kondensatorenergie
Abbildung 2.4.j
linear
zur
Anzahl
der
Radumdrehungen an. Da diese Energie mit der
Formel
1
E= c⋅U 2 ,
2
beschreibt
der
Graph
berechnet
der
wird,
Spannung
des
Kondensators also eine Wurzelfunktion.
In Abbildung 2.4.f wurde eine Schaltung mit zwei
Dioden verwendet, die der in Abbildung 2.4.e
Abbildung 2.4.k
unten links dargestellten Schaltung entspricht.
Diese verhindert lediglich das Entladen des
Kondensators.
Nachdem
der
Schallwandler
jedoch bei der ersten Belastung seine Spannung
größtenteils an den Kondensator abgegeben hat,
lädt er sich bei der folgenden Drucksenkung
umgekehrt auf. Die nächste Druckerhöhung,
Abbildung 2.4.l
wenn der Schallwandler wieder auf den Boden
gedrückt
wird,
reicht dann nur aus,
um die umgekehrte
Ladung
wieder
abzubauen,
nicht,
um
den
Kondensator weiter
zu
laden.
lässt
Damit
sich
geringe
die
erzeugte
Spannung
Abbildung 2.4.m
begründen.
~ 21 ~
Dass
der Kondensator überhaupt geladen wird, könnte an der Ungleichheit der Belastungen oder
Entladung des Schallwandlers liegen.
Die den in Abbildung 2.4.g dargestellten Werten zugrunde liegende Schaltung besteht aus drei
Dioden und ist in 2.4.e oben rechts gezeigt. Die dritte Diode erlaubt eine Entladung des
Schallwandlers und verhindert damit das umgekehrte Aufladen. Damit ist der Generator jeweils vor
der Belastung ungeladen und die Belastung wird komplett zum Spannungsaufbau genutzt.
Die effektivste getestete Schaltung ist der Brückengleichrichter, bei dem zusätzlich zu den beiden
immer verwendeten Dioden weitere zwei Dioden über Kreuz zum jeweiligen Pol des Kondensators
führen. Somit wird beim Entlasten nicht nur der Schallwandler entladen, sondern auch diese
Druckänderung zum Laden des Kondensators genutzt.
Bei sehr großen Spannungen am Kondensator steigt die Energiezunahme etwas langsamer an. Das
kann neben den Kondensatoreigenschaften auch als Grund haben, dass der Kondensator immer nur
dann geladen wird, wenn U Kondensator <U Schallwandler , was bei höheren Spannungen am Kondensator
nur in kleineren Zeitabschnitten der Fall ist. Dieses langsamere Ansteigen fällt vor allem in
Abbildung 2.4.h auf.
Verschiedene Kräfte auf den Reifen:
Abbildung 2.4.n
Wie schon im Versuch 2.4.2 angedeutet, sind die verwendeten Schallwandler bei großen Drücken
sehr ineffizient. Daher sind beim Fahren, bei dem ca. 300 N auf den Piezo-Generator wirken, die
erzeugten Spannungen am Kondensator nur insignifikant größer als beim Schieben, bei dem
lediglich 60 N bzw. 120 N auf den Reifen wirken.
Hier ist also noch sehr viel Potential, mit geeigneteren Piezo-Generatoren deutlich effizienter mehr
Energie zu generieren.
~ 22 ~
Verschiedene Kondensatoren:
Auch
die
Kapazität
des
verwendeten
Kondensators hat einen großen Einfluss darauf,
wie viel Energie mit dem gleichen Aufwand
gespeichert wird.
Abbildung
2.4.k
Energieverlauf
beim
zeigt
Spannungs-
Radfahren
mit
und
einem
Brückengleichrichter und einem Kondensator der
Kapazität
c=470μF
und
entspricht
daher
Abbildung 2.4.o
abgesehen von der Kapazität des Kondensators
genau dem in 2.4.h dargestellten Versuch.
Wie in Abbildung 2.4.l dargestellt, kann der
Kondensator mit der etwas mehr als doppelt so
großen Kapazität nur ungefähr ein Sechzigstel
der
Energie
speichern,
die
am
anderen
Kondensator gemessen wurde. Ein weiterer
Abbildung 2.4.p
Versuch mit einem Goldcap-Kondensator mit einer Kapazität von 0,2 F bestätigt ebenfalls die
These: Je größer die Kapazität des verwendeten Kondensators, desto mehr Energie geht beim
Speichern verloren.
Das liegt an der kleinen Kapazität des Schallwandlers: Entlädt sich ein Kondensator auf einen
anderen, dann sinkt die Spannung linear zur Erhöhung der Kapazität. Die elektrische Energie ist
aber proportional zum Quadrat der Spannung. Bei einem deutlichen Unterschied der Kapazitäten
geht also viel Energie verloren.
Dieses Problem kann durch Erhöhen der Kapazität des Generators abgeschwächt werden. Besteht
dieser aus vielen sehr dünnen Schichten, ist seine Kapazität deutlich größer, die Differenz der
Kapazitäten daher kleiner und damit auch der Energieverlust verringert.
Auch hier befindet sich also noch großes Verbesserungspotential zwischen der Versuchsreihe und
einer möglichen technischen Anwendung.
Mögliche Messfehler und -ungenauigkeiten:
Die Kräfte auf die Schallwandler sind so groß, dass durch starkes Verbiegen des Schallwandlers die
Piezokeramikschicht aufreißt und die Effizienz nachlässt. Die Schallwandler wurden zwar oft
ausgetauscht, neue Piezo-Generatoren erzeugen dennoch jeweils etwas höhere Werte.
~ 23 ~
2.4.6 Schallwandler in Schuhen
Schuhe sind ein weiteres Beispiel für Gegenstände, in denen sich mechanischer Druck alltäglich
sehr oft ändert. Damit sind auch Schuhe potentiell für Energy Harvesting mittels piezoelektrischem
Effekt geeignet.
Ein Schallwandler wird zentral in die
Schuhsohle zwischen Einlage und Sohle
eingebaut und über Kabel und einen
Brückengleichrichter mit einem GoldcapKondensator der Kapazität 0,2 F verbunden,
wobei Dioden und Kondensator auf dem
Schuh befestigt sind.
Ähnlich der Anwendung am Fahrradreifen
steigen und sinken bei jedem Schritt die
Kraft und der Druck auf die Schuhsohle und
Abbildung 2.4.q
somit auf den Piezo-Generator.
An einem normalen Tag mit durchschnittlicher Bewegung können so trotz der gleichen Verluste wie
am Fahrrad rund 1,5 mJ erzeugt werden.
2.5 Fazit
Auf den ersten Blick legen die sehr kleinen gemessenen Energiemengen einen großflächigeren
Einsatz in der Technik nicht nahe.
Allerdings existiert noch enormes Verbesserungspotential. Die verwendeten Schallwandler sind bei
großen Kräften extrem ineffizient, beim Laden des Kondensators geht durch die Differenz der
Kapazitäten viel Energie verloren und sowie im Schuh als auch am Reifen wurde ein einzelner
Piezo-Generator betrachtet, obwohl die nutzbaren Flächen, auf denen Druckänderungen stattfinden,
deutlich größer sind.
Außerdem zeigen die Versuche, dass die Energie nach dem Prinzip des Energy Harvesting ohne
jegliche Aufwandssteigerung gewonnen werden kann.
Für Anwendungen, bei denen kleine elektrische Energiemengen benötigt werden, ist ein Einsatz von
Piezo-Generatoren also durchaus denkbar. Solche Anwendungen könnten das Aufladen von kleinen
Akkus oder der energieautarke Betrieb kleiner elektrischer Geräte sein.
Großflächige Einsätze können durch die Versuche nicht begründet werden, scheinen aber, wie das
israelische Unternehmen Innowattech zeigt, auch möglich.
~ 24 ~
Quellen
1
Bergmann, Ludwig:
Lehrbuch der Experimentalphysik / Bergmann-Schaefer. - Berlin ; New York : de Gruyter
NE: Schaefer, Clemens:
Bd. 2. Elektrizität und Magnetismus / von Heinrich Gobrecht. Unter Mitarb. Von Jens H.
Gobrecht u. Klaus H. Gobrecht. 7. Aufl., neubearb. u. Erw. - 1987.
ISBN 3-11-010261-7
NE: Gobrecht, Heinrich [Bearb.]
2
APC International, Ltd. (Hrsg.): Piezoelectric Ceramics. Principles and Applications.
Second Edition.
3
http://www.piezo.de/pdf/PIC_Piezoelektrische_Materialien_c.pdf, 5.7.2014, 13:00
4
http://www.keramverband.de/keramik/pdf/05/sem05_04.pdf, 5.7.2014, 13:00
5
http://daten.didaktikchemie.uni-bayreuth.de/umat/piezo/piezo_effekt.htm, 5.7.2014, 13:00
6
http://www.piezoeffekt.de. 5.7.2014, 13:00
7
http://www.mineralienatlas.de/lexikon/index.php/Elementarzelle, 5.7.2014. 13:00
8
http://de.wikipedia.org/wiki/Seignettesalz, 5.7.2014, 13:00
9
http://www.youtube.com/watch?v=E1Ct3VUWvhQ, 5.7.2014, 13:00
10
http://www.youtube.com/watch?v=R9m79oWdOZI, 5.7.2014, 13:00
11
http://www.diss.fu-berlin.de/diss/servlets/MCRFileNodeServlet/
FUDISS_derivate_000000001533/05_kapitel_5.pdf?hosts, 5.7.2014, 13:00
12
http://www.greenprophet.com/2008/12/israel-innowattech-electricity/, 5.7.2014, 13:00
13
http://www.juedische-allgemeine.de/article/view/id/5383, 5.7.2014, 13:00
14
http://www.google.de/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&ved=0CdwQFjAC
&url=http%3A%2F%2Fwww.enocean.com%2Ffileadmin%2Fredaktion%2Fpd%2Fperpetu
um%2Fperpetuum_01_de.pdf&ei=U4SMU9O9BKSp4gTai4DwCA&usg=AFQjCNFnwIA
ns34PqmXVKQ27KHspUMgfAA&bvm=bv.67720277,d.bGQ, 5.7.2014, 13:00
15
http://innowattech.co.il, 5.7.2014, 13:00
16
http://www.helpster.de/elektrofeuerzeug-funktion_171346, 5.7.2014, 13:00
17
http://de.wikipedia.org/wiki/Funke_%28Entladung%29, 5.7.14, 13:00
~ 25 ~