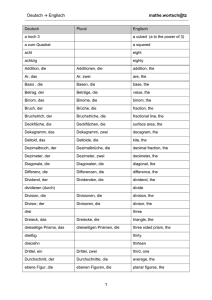
1. Wortschatz in Geometrie (1)

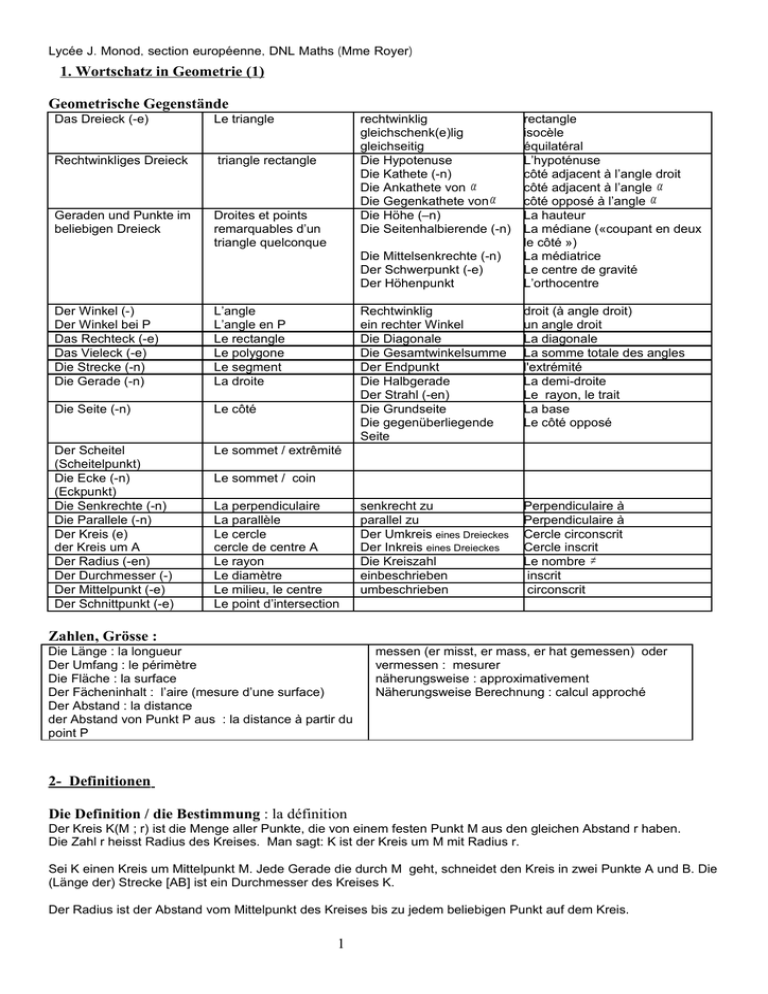
Lycée J. Monod, section européenne, DNL Maths (Mme Royer)
1. Wortschatz in Geometrie (1)
Geometrische Gegenstände
Das Dreieck (-e)
Le triangle
Rechtwinkliges Dreieck
triangle rectangle
Geraden und Punkte im
beliebigen Dreieck
Droites et points
remarquables d’un
triangle quelconque
rechtwinklig
gleichschenk(e)lig
gleichseitig
Die Hypotenuse
Die Kathete (-n)
Die Ankathete von α
Die Gegenkathete von α
Die Höhe (–n)
Die Seitenhalbierende (-n)
Die Mittelsenkrechte (-n)
Der Schwerpunkt (-e)
Der Höhenpunkt
Der Winkel (-)
Der Winkel bei P
Das Rechteck (-e)
Das Vieleck (-e)
Die Strecke (-n)
Die Gerade (-n)
L’angle
L’angle en P
Le rectangle
Le polygone
Le segment
La droite
Die Seite (-n)
Le côté
Der Scheitel
(Scheitelpunkt)
Die Ecke (-n)
(Eckpunkt)
Die Senkrechte (-n)
Die Parallele (-n)
Der Kreis (e)
der Kreis um A
Der Radius (-en)
Der Durchmesser (-)
Der Mittelpunkt (-e)
Der Schnittpunkt (-e)
Le sommet / extrêmité
rectangle
isocèle
équilatéral
L’hypoténuse
côté adjacent à l’angle droit
côté adjacent à l’angle α
côté opposé à l’angle α
La hauteur
La médiane («coupant en deux
le côté »)
La médiatrice
Le centre de gravité
L’orthocentre
Rechtwinklig
ein rechter Winkel
Die Diagonale
Die Gesamtwinkelsumme
Der Endpunkt
Die Halbgerade
Der Strahl (-en)
Die Grundseite
Die gegenüberliegende
Seite
droit (à angle droit)
un angle droit
La diagonale
La somme totale des angles
l'extrémité
La demi-droite
Le rayon, le trait
La base
Le côté opposé
senkrecht zu
parallel zu
Der Umkreis eines Dreieckes
Der Inkreis eines Dreieckes
Die Kreiszahl
einbeschrieben
umbeschrieben
Perpendiculaire à
Perpendiculaire à
Cercle circonscrit
Cercle inscrit
Le nombre π
inscrit
circonscrit
Le sommet / coin
La perpendiculaire
La parallèle
Le cercle
cercle de centre A
Le rayon
Le diamètre
Le milieu, le centre
Le point d’intersection
Zahlen, Grösse :
Die Länge : la longueur
Der Umfang : le périmètre
Die Fläche : la surface
Der Fächeninhalt : l’aire (mesure d’une surface)
Der Abstand : la distance
der Abstand von Punkt P aus : la distance à partir du
point P
messen (er misst, er mass, er hat gemessen) oder
vermessen : mesurer
näherungsweise : approximativement
Näherungsweise Berechnung : calcul approché
2- Definitionen
Die Definition / die Bestimmung : la définition
Der Kreis K(M ; r) ist die Menge aller Punkte, die von einem festen Punkt M aus den gleichen Abstand r haben.
Die Zahl r heisst Radius des Kreises. Man sagt: K ist der Kreis um M mit Radius r.
Sei K einen Kreis um Mittelpunkt M. Jede Gerade die durch M geht, schneidet den Kreis in zwei Punkte A und B. Die
(Länge der) Strecke [AB] ist ein Durchmesser des Kreises K.
Der Radius ist der Abstand vom Mittelpunkt des Kreises bis zu jedem beliebigen Punkt auf dem Kreis.
1
Lycée J. Monod, section européenne, DNL Maths (Mme Royer)
3- Sätze :
Der Satz : le théorème
a) Der Satz des Pythagoras (Satz von Pythagora)
Im rechtwinkligen Dreieck ist das Quadrat der Hypotenuse gleich die Summe der Quadraten der Katheten.
Bezeichnen wir mit A, B und C die Ecken des Dreieckes, wo der Winkel bei C ein rechter Winkel ist.
Also gilt die Formel : AB 2 = AC 2 + CB 2
Beweis: www.beweiskompendium.de.vu
b) Streckenverhältnisse des Strahlensatzes:
Der 1. Strahlensatz: Werden zwei von einem Punkt S ausgehende Strahlen von zwei Parallelen geschnitten, so
verhalten sich die Abschnitte auf dem einen Strahl wie die entsprechende Abschnitte auf dem anderen.
Der 2. Strahlensatz: Werden zwei von einem Punkt S ausgehende Strahlen von zwei Parallelen geschnitten, so
verhalten sich die Abschnitte auf dem einen Strahl wie die entsprechende Abschnitte auf den Parallelen.
Strahlensatz (de.wikipedia.org)
Wenn zwei durch einen Punkt (Scheitel) verlaufende Halbgerade (Strahlen) von zwei Parallelen geschnitten werden,
die nicht durch den Scheitel gehen, dann gelten die folgende Aussagen:
1.
Es verhalten sich je zwei Abschnitte auf dem einen Strahl zueinander so wie ihnen entsprechenden
Abschnitte auf dem anderen Strahl. Also gilt: ...
2.
Es verhalten sich die ausgeschnittenen Strecken auf den Parallelen, wie die ihnen entsprechenden, wom
Scheitel aus gemessenen Strecken auf den Strahlen. Also gilt: ...
3.
Umkehrung des ersten Strahlensatzes: Ist Eigenschaft 1. erfüllt, so kann man auf parallele Geraden
schliessen.
Eine V-Figur :
Eine X-Figur:
C
C
D
D
S
A
A
B
B
S
Bemerkung : ist dagegen Eigenschaft 2. gegeben, so ist keiner Schluss auf Parallelität möglich!
Beweis: www.beweiskompendium.de.vu ; http://de.wikipedia.org/wiki/Strahlensatz
Anwendung : http://de.wikipedia.org/wiki/Daumensprung eine Methode, um den Abstand zwischen dem beobachter und einemen
beobachtbaren Objekt oder dessen Grösse zu schätzen
.http://de.wikipedia.org/wiki/Strahlensatz#Einfaches_Anwendeungsbeispiel Höhe der Cheops Pyramide
2
Lycée J. Monod, section européenne, DNL Maths (Mme Royer)
4- Wortschatz für mathematische Beweise
beweisen : prouver, démontrer
der Beweis (-e): la preuve, la démonstration
einer Sache zugrunde liegen : être à la base de qqchose
daraus folgt : de cela il découle
man kann daraus folgern / schliessen : on peut en déduire / conclure
die Folge / die Konsequenz : la conséquence
die Schlussfolgerung / der Schluss : la conclusion
eine Schlussfolgerung ziehen : tirer une conclusion
es gilt die folgende Formel : on a la formule suivante ; la formule suivante est vraie / valable
es gelten die folgenden Aussagen : les énoncés suivants sont vrais
es ergibt sich die Gleichheit / den Wert ... : il en résulte l’égalité / la valeur...
daraus ergibt sich für alle Dreiecke die Formel : donc pour tout triangle on obtient la formule
die Annahme : l’hypothèse, la supposition
die Voraussetzung : l’hypothèse, le présupposé
die Grundvoraussetzung : l’hypothèse de base
die Behauptung : l’affirmation
nehmen wir an dass ... : supposons que ...
angenommen dass... : à supposer que ...
die Eigenschaft : la propriété
die Rechenregel : la règle de calcul
das Gesetz : la propriété ; la loi
die Beziehung : la relation
beziehungsweise (bzw) : respectivement
Nach dem Satz ** gilt: d’après le théorème ** on a :
umgekehrt : réciproquement
Die Umkehrung : la réciproque
also / folglich / daher : donc , en conséquence
denn : car
weil etw. passiert : parce que …
wenn etw. passiert, dann ist etw. wahr : si … alors
anderenfalls / sonst / ansonsten / wenn nicht : sinon
da / dann : alors
deshalb : c’est pourquoi
sich mit etw. befassen : se (pré)occuper de
es handelt sich um : il s’agit de
angenommen, es wäre nicht so : supposons le contraire
das widerspicht der Annahmme ... : cela contredit l’hypothèse
Dieses ist ein Widerspruch, also muss die Annahme flasch sein. Ceci est une contradiction ...
eine Hypothese aufstellen : élaborer une hypothèse

Am Ende eines Beweises schreibt man : w.z.b.w. (was zu beweisen war)
das bedeudet gar nicht „Was zu bezweifeln wäre"!
3