Impulssatz für Systeme von Teilchen

2.7.3 Impulssatz fur Systeme von Teilchen
Mit den Bezeichnungen P~ fur den totalen Impuls des Systems, und F~ fur die resultierende
aussere Kraft, liest sich das 2. Newton'sche Prinzip fur ein System von Teilchen auch als
P~ =
X ~p
n
i
i
=1
F~ =
X F~
~
F~ = ddtP
n
i
=1
i
Obwohl diese Gleichung, die man den Impulssatz nennt, mit dem 2. Newton'schen Prinzip
der Form nach identisch ist, ist der Inhalt dieser Gleichung ein anderer. Wirken auf ein System
keine ausseren Krafte, d. h. F~ = 0, so nennt man dieses System abgeschlossen.
Fur ein abgeschlossenes System gilt
i
dP~ = 0
dt
P~ = const.
)
Der totale Impuls eines abgeschlossenen Systems ist konstant
Der Impuls ist eine sogenannte Konstante der Bewegung.
2.7.4 Kinetische Energie und Arbeit bei Translation
Die kinetische Energie eines Systems von Massenpunkten ist gegeben durch
T=
XT = X m v
i
2
i
i
i
2
i
Fur eine kontinuierliche Massenverteilung muss jeweils die Summe uber die Massenpunkte durch
ein Integral ersetzt werden,
T = 12 v 2dM
Z
M
Fur starre Korper ist die kinetische Energie im speziellen Fall reiner Translation, bei der alle Geschwindigkeiten ~v gleich gross sind, und damit auch ~v = ~v
gilt, gegeben durch
i
T =
S
i
Xmv
v
=
2
2
i
i
2
i
2
S
Xm = M v
i
i
~v2
;
ZZ ; ~v ~v3
~v1 ZZr;; ;;
;((((S((ZZ(u;
;
3
r(;(
2;
s;
S
2
S
2
S
1
Ein starrer oder beweglicher Korper kann aber auch noch eine Rotation ausfuhren. Auf die
Drehungen kommen wir in Kurze zuruck.
Wirken auf ein System von Massenpunkten mehrere Krafte F~ , so leistet jede einzelne die
Arbeit
dW = F~ d~r
j
j
j
2.93
j
Der Massenpunkt j , an dem die Kraft F~ angreift, wird um d~r verschoben. Die gesamte am
System geleistete Arbeit dW ist die Summe
j
dW =
j
X dW = X F~ d~r
j
j
j
j
j
Bei reiner Translation eines starren Korpers sind alle d~r gleich d~r und es gilt
X
X
dW = F~ d~r = d~r F~ = F~ d~r
j
j
j
S
j
j
S
S
j
Die gesamte, von allen Kraften geleistete Arbeit ist gleich der Arbeit, welche die resultierende
Kraft F~ bei der Schwerpunktsverschiebung d~r leistet, genau wie wir dies fur den Massenpunkt
gefunden haben. Da die inneren Krafte G~ jeweils einen Reaktionspartner G~ haben, fur den
gilt G~ = ;G~ , heben sich die Terme G~ d~r + G~ d~r gerade gegenseitig auf.
Wenn wir vom Schwerpunktssatz ausgehen, dann lasst sich die geleistete Arbeit mit der
A nderung der kinetischen Energie der Schwerpunktsbewegung verknupfen:
d~p = F~ ) M 2 ~v ~v dt = 2 F~
~ v dt = 1 M (v2 2 ; v 2 1) = 2 F~ d~r
dt
2
1 dt
1
1
Die gesamte von allen Kraften geleistete Arbeit ist gleich der Arbeit, welche die resultierende
Kraft am Schwerpunkt leistet und gleich der A nderung der kinetischen Energie der Translationsbewegung des Schwerpunkts:
S
ki
ki
ik
ki
Z
S
ik
S
ik
Z
S
Z
S
dW = dT
S
S
S
S
T 2 ; T 1 = W1!2
S
S
Z
=
1
S
S
2
F~ d~r
S
Diese Beziehung, die wir hier als Integral des Schwerpunktssatzes erhalten haben, und die
wieder formell mit derjenigen fur den einzelnen Massenpunkt identisch ist, gilt nur, wenn der
Korper starr ist, und die Bewegung einer reinen Translation (nicht notwendigerweise geradlinig)
entspricht. Dass diese Bedingungen notwendig sind, wollen wir an zwei einfachen Gedankenexperimenten illustrieren.
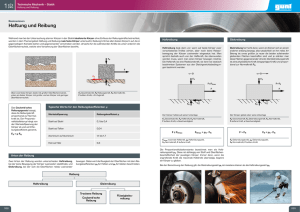
Zwei ruhende Massen m1 = m2 = m werden auseinandergezogen von
zwei gleichen, aber entgegengesetzten Kraften: F 1 = ;F 2 = F . Das
Integral des Schwerpunktssatzes liefert
F 1 d d- F 2
m m1
(F 1 + F 2 )x = 0 = 2 (2m)v 2 = 0
m1 m2
Der Schwerpunkt bleibt in Ruhe. Dafur muss keine Arbeit aufgewendet werden. Trotzdem
wird Arbeit geleistet, denn jede einzelne Masse wird um d bewegt und erhalt die Geschwindigkeit
v: F d = mv 2=2. Die gesamte Arbeit ist also 2F d = mv2. Hier haben wir es nicht mit einem
starren Korper und auch nicht mit reiner Translation zu tun. Das Integral der Schwerpunktssatzes liefert nur die fur die Bewegung des Schwerpunkts notwendige Arbeit, nicht die gesamte
Arbeit.
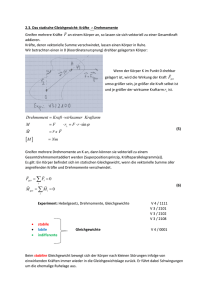
Ein zweites Beispiel ist eine aufgerollte Kette, die in einem kleinen Haufen auf einem reibungslosen Boden ruht und durch eine konstante Kraft auseinandergezogen und auf eine Geschwindigkeit v gebracht wird. Die Verschiebung des Angrispunkts der Kraft ist grosser als die
x
x
x
x
x
x
x
S
S
x
2.94
x
des Schwerpunkts. Der Schwerpunktssatz liefert Fd = mv 2 =2 als Arbeit fur die Schwerpunktsbewegung. Die gesamte Arbeit ist jedoch Fd = F (d + L=2) > Fd . Auch hier ist das System
nicht starr. Ein Teil der am System geleisteten Arbeit wird nicht in kinetische Energie verwandelt. Die Energiebilanz stimmt erst wieder, wenn man andere Energieformen berucksichtigt.
Hier ist es Energie, die beim Auseinanderziehen der Kette zu Stossen
L
unter den Kettengliedern, Deformationen und schliesslich zu leichter
ds
F
v
Erwarmung der Kette fuhrt. Wir konnen aus der beobachteten kiS s
d
netischen Energie nur jenen Teil der Arbeit abschatzen, der fur die
Schwerpunktsbewegung notwendig ist.
S
S
s
s
Zusammenfassung: Systeme von Teilchen, starre Korper
Denition des Schwerpunkts:
X m ~r = Ortsvektor des Schwerpunkts
X
= Geschwindigkeit des Schwerpunkts
M= m =
~r = M1
S
d~r = ~v
dt
S
S
i
i
i
Totaler Impuls und resultierende aussere Kraft:
P~ =
totale Masse
i
i
X p~ = X m ~v M~v
i
i
i
i
S
F~ =
;
i
X F~ = X d~p = d X ~p = dP~
i
dt
i
i
i
dt
i
i
Abgeschlossenes System: Der totale Impuls ist konstant.
~
F~ = 0 = ddtP ) P~ = const:
Schwerpunktssatz:
F~ =
X F~ = M d~v
dt = M~a
S
i
i
S
Kinetische Energie und Arbeit:
T = 12
Xm v = XT
2
i
dW =
i
i
i
i
X F~ d~r = X dW
i
i
i
Kinetische Energie bei reiner Translation:
T = 21
T
Xm v = XT = 1 Xm v
i
2
i
i
i
i
2
i
2
S
i
~v = ~v , ~v = Schwerpunktsgeschwindigkeit
i
S
S
Arbeit-Energie Beziehung bei reiner Translation:
1
2
2
2 M (v 2 ; v 1 ) =
S
S
2.95
Z
2
1
i
F~ d~r
S
= 21 Mv 2
S
i
dt
2.7.5 Beispiele zum Schwerpunktssatz und Impulssatz
2.7.5.1 Bewegungen von Menschen und Tieren
Nach dem 2. Newton'schen Prinzip oder dem Schwerpunktssatz beginnt sich ein Korper
in Bewegung zu setzen, wenn auf ihn eine Kraft von aussen einwirkt. Innere Krafte dagegen
heben sich auf und tragen nicht zur Beschleunigung bei. Lebewesen sind aber in der Lage \sich
selber" in Bewegung zu setzen, sind also in einem gewissen Sinn \automobil". Ist dies mit dem
2. Newton'schen Prinzip vertraglich?
Die Antwort auf diese Frage ist eindeutig \Ja". Eine genauere U berlegung zeigt, dass in
allen Fallen eine aussere Kraft die Beschleunigung bewirkt. Der Unterschied zwischen passiver
und aktiver Fortbewegung besteht nur darin, dass im zweiten Fall der beschleunigte Korper
die aussere Kraft selber hervorruft und willentlich vergrossern oder verkleinern kann. Dies
ist moglich dank des 3. Newton'schen Prinzips. Dadurch, dass ein Korper eine Kraft auf
einen andern ausubt, erreicht er, dass der andere auf ihn selber eine entgegengesetzt gleiche
Kraft ausubt, welche ihn beschleunigen kann. In den meisten Fallen handelt es sich dabei um
Reibungs- und Normalkrafte, d. h. Oberachenkrafte elektromagnetischen Ursprungs.
Voraussetzung dafur, dass ein Korper sich selber in Bewegung setzt, ist, dass er nicht starr
ist, sondern aus Teilen besteht, die durch innere, von einem Willen gesteuerte Krafte gegeneinander bewegt werden konnen (Kniebeugen, Neigen des Oberkorpers, Drehung der Rader eines
Fahrzeugs). Dies allein genugt jedoch nicht. Ein aufgebocktes Auto oder ein Auto auf Glatteis
setzt sich bei noch so schnell drehenden Radern nicht in Bewegung. Dasselbe gilt fur einen Rollschuhlaufer auf reibungsfreier, horizontaler Unterlage. Solange keine ausseren Krafte wirken,
bleibt der Schwerpunkt in Ruhe, auch wenn die Korperteile gegeneinander beschleunigt sind. Sobald diese Teile bei ihrer Bewegung jedoch auf die Umgebung, z. B. die Unterlage Reibungs- oder
Normalkrafte ausuben, treten Reaktionskrafte auf den Korper auf und beschleunigen ihn. Die
Normalkraft (= Normalkomponente der Beruhrungskraft) auf horizontaler Unterlage ermoglicht
allerdings nur vertikales Hupfen.
RH
NH
S
RB
NB
G
G
N1
R
H;B ein
R
=
H;tot
H;Bein
N
Bein;S eil
;R
H;H and
=
H;H and
N
H and;Seil
= N ; G N ; < 1; ) N > G
H
tot
H
tot
tot
H
N2
G~ = N~ 1 + N~ 2 = N~
tot
)
N =G
tot
Abbildung 2.50: Treppensteigen ist okonomischer als ein Seil hochklettern.
Wir konnen somit schliessen, dass die beschleunigte Bewegung eines \ sich selbst" bewegen2.96
den Korpers auf Kraften beruht, die aus der Umgebung auf ihn ausgeubt werden. Im kraftefreien,
leeren Raum kann sich zwar eine Rakete scheinbar beschleunigt bewegen, der Schwerpunkt des
gesamten Systems Brennsto plus Kapsel bleibt in Ruhe oder er bewegt sich gleichformig. Das
Ausstossen des Brennstos mit hoher Relativgeschwindigkeit fuhrt lediglich dazu, dass sich die
Kapsel immer weiter vom ruhenden Schwerpunkt entfernt.
Im Laufe seiner langen Evolutionsgeschichte hat der Mensch (und auch andere Lebewesen)
gelernt, welche Krafte sich am okonomischsten fur die Fortbewegung einsetzen lassen. Wir wollen
dazu ein paar Bewegunsablaufe naher untersuchen, und auch Arbeits- und Energiebetrachtungen
einschliessen.
U berwinden einer Hohendierenz: Der Vergleich von Klettern und Treppensteigen
zeigt, dass im ersten Fall, die vom Korper auf das reagierende Medium auszuubende Normalkraft
grosser sein muss als das Gewicht, im zweiten Fall hochstens aber gleich gross (siehe Abbildung
2.50).
Start eines Sprinters: Ohne Startblocke ist die maximale Beschleunigung durch den Haftreibungskoezienten beschrankt, mit Startblocken hat die Normalkraft eine Komponente in
Bewegungsrichtung (Abbildung 2.51). Die Beschrankung durch den Haftreibungskoezienten
entfallt.
S
G
N
N
RH
Mit Startblöcken
Ohne Startblöcke
a mN = g
H
x
H
a = R sin + N cos ; R N; a mg ( sin + cos )
x
H
H
H
x
H
Abbildung 2.51: Zum Nutzen von Startblocken.
Bergsteigen Wir wollen uns mit vier typischen Situationen auseinandersetzen, die man
beim Bergsteigen antreen kann. Die folgende Diskussion stammt aus Scientic American,
Juni 1989, p. 92 - 95, J. Walker, The Amateur Scientist: The mechanics of rock climbing or
surviving the ultimate physics exam. In allen Fallen ist uns intuitiv wahrscheinlich das richtige
Verhalten vertraut. Diese Intuition wollen wir aber auch physikalisch begrunden. Die erste
U berlegung betrit die Entscheidung, ob man einen Berg am leichtesten uber eine Grat oder
uber eine Flanke ersteigt, wenn die Felsbeschaenheit und andere Bodeneigenschaften gleich
sind. Die zweite betrit die optimale Haltung beim Steigen an einem gewohnlichem Hang, soll
man sich mit den Handen aufstutzen um die Sicherheit zu erhohen oder nicht ? Die dritte
betrit das Erklettern eines Kamins, die vierte schliesslich eine Spalte.
Zum Einstieg untersuchen wir zunachst die Situation gewohnlichen Gehens und Stehens auf
einem Abhang und in der Ebene (siehe Abbildung 2.52). Wir bezeichnen mit die Neigung
des Abhangs und die mit den Reaktionswinkel. Dieser ergibt sich aus der Reibungskraft des
2.97
Bodens (Fels) auf die Person R , die durch eine selbsterzeugte Schubkraft der Person (S )
auf den Boden erzeugt oder vergrossert wird, und die Normalkraft des Bodens auf die Person
N :
R
tan = N
Im Fall des Gehens in der Ebene ist
N =G
R =S N = G
Solange die Bedingung tan erfullt ist, rutscht der Schuh nicht auf der Unterlage. Beim
Stehen am Abhang gilt
N = G cos R = G sin und damit tan = tan Wenn und damit grosser wird, beginnt man abzurutschen. Beim Ansteigen wir die Reibung
durch die selbsterzeugte Schubkraft vergrossert, und damit der Reaktionswinkel ebenfalls. Maximal kann der Reaktionswinkel wieder tan = erreichen. Zu hartes Schieben fuhrt wieder
zum Gleiten.
FP
FP
FP
FP
FP
FP
FP
PF
H
FP
H
H
FP
FP
H
Schwerpunkt
Gewicht
G
Reibung
RFP
Reaktionskraft
α
Reaktionskraft
Gewicht
G
Reaktionswinkel
Normalkraft
NFP
Schub
Reibung
SPF
Komponenten
des Gewichts
Reaktionskraft
nach vorne
geneigt
Normalkraft
NFP
Reaktionswinkel=
Neigungswinkel
β
Reibung
grössere
Reibung
grösserer
Reaktionswinkel
Schub
Abbildung 2.52: Links: Gehen in der Ebene. Mitte: Stehen am Hang. Rechts: Gehen am
Hang. Die eingezeichneten Krafte sind das Gewicht (G~ ), die Normalkraft des Bodens (Fels) auf
die Person (N~ ), die Reibungskraft des Bodens auf die Person (R~ ) und die selbsterzeugte
Schubkraft der Person auf den Boden (S ). Letztere greift am Boden an.
FP
FP
PF
Mit diesen Kenntnissen ist es klar,
dass man die besten Chancen hat,
den kritischen Reaktionswinkel nicht
zu uberschreiten, wenn die Neigung des
Hangs moglichst kleine ist. Bei dem
gezeichneten Berg ist die Neigung am
Grat am kleinsten, denn die Hypotenuse des rechtwinkligen Dreiecks ist
langer als die Kathete.
2.98
Vom Bucken und Aufstutzen der Hande wird abgeraten. Die Reibungskrafte mussen wieder
die Komponente des Gewichts entlang des Hangs (siehe Abbildung 2.53) aufheben. Die Reibung
der Hande auf dem Fels ist in der Regel kleiner als die guter Schuhe. Wenn man an den Handen
den Halt verliert, bleiben nur noch die Reibungskrafte an den Fussen. Auch wenn diese beim
Aufrechtstehen ausreichen mogen, konnen sie beim Vorwartsbeugen kleiner sein. Um dies zu
verstehen, mussen wir noch eine weitere Stabilitatsbedingung, die wir in den Abschnitten 2.8.4
und 2.9 naher untersuchen benutzen, die Drehmoment-Bedingung.
Wir fuhren die Drehmomentbedingung hier ad hoc, an Mittelschulbegrie erinnernd ein. Wenn wir an den Enden eines Stabs ziehen, der
Ou
in einem Punkt O gelagert ist, so wird sich der Stab nur dann nicht
F~1 d1 d2
drehen, wenn F1 d1 ; F2 d2 = 0 gilt. Dies ist eine Anwendung des Dralloder Drehimpulssatzes, aus der Mittelschule eventuell als Hebelgesetz
?
F~2
bekannt. F d sind die Drehmomente der Krafte, die hier sich aus dem
?
Produkt des Abstands der Wirkungslinie der Kraft zum Drehpunkt und
der Kraft ergeben.
i
i
Punkt mit Drehmoment:0
Normalkraft
NFP
Gewicht
G
Normalkraft
NFP
Reibung
Reibung
Abbildung 2.53: Stark gebuckte und fast aufrecht stehende Person am Hang mit aufgestutzten
Handen (fur die Bezeichnung der Krafte siehe Abbildung 2.52).
Um Stabilitat des Bergsteigers gegen eine Drehung um irgendeinen Punkt zu erreichen,
muss die Summe der Drehmomente verschwinden. Diese Bedingung lasst sich auf die folgende
einfache Aussage reduzieren. Wenn die Angrislinien der beiden Reaktionskrafte (Hand und
Fuss) und des Gewichts sich in einem Punkt treen (alle d sind dann null bezuglich dieses
Punkts) verschwinden die Drehmomente auch fur jeden anderen Bezugspunkt. Aus dem Bild
ist ersichtlich, dass das fur die Reaktionskraft am Fuss beim Neigen nach vorne einen grosseren
Reaktionswinkel erfordert und damit eine grossere Chance zulasst, den kritischen Winkel zu
uberschreiten.
Man kann im ubrigen aus den drei Bedingungen (Kraftegleichgewicht in zwei Koordinatenrichtungen und Drehmomentenbedingung) fur diesen Fall die Normalkrafte nicht eindeutig
bestimmen, denn wir haben vier unbekannte Kraftkomponenten fur die Hande und die Fusse.
Nur die genaue Kenntnis der Muskelkrafte kann uns da weiter helfen. Ausserdem ist aus Abbili
2.99
dung 2.52 ersichtlich, dass fur die Stellung mit den relativ weit nach vorne aufgestutzten Handen
die Reaktionskraft leicht abwarts zeigt, die Reibung ebenfalls. Die Reibung an den Fussen muss
daher nicht nur die Komponente des Gewichts parallel zum Hang, sondern auch die Reibung an
den Handen kompensieren, was die Gefahr des Abrutschens noch erhoht. Die Haltung auf der
rechten Seite von Abbildung 2.53 erweist sich bei genauer Analyse als aufrechtes Stehen.
Punkt mit
Drehmoment:0
Reibung
Reaktionswinkel
Normalkraft
Reibung NFP
Reaktionswinkel
Normalkraft
Gewicht
NFP
Füsse tiefer
Füsse höher
Abbildung 2.54: Links: Optimale Stellung beim Ausruhen wahrend des Kletterns im Kamin.
Links: Position mit tiefer gestellten Fussen. Rechts: Position mit hoher gestellten Fussen (fur
die Bezeichnung der Krafte siehe Abbildung 2.52).
Wenn ein Kletterer beim Anstieg in einem Kamin eine Ruhepause einschalten will (Abbildung 2.54), dann ist dies am erholendsten, wenn die Normalkrafte moglichst klein sind. Man
ndet eine Position, bei der die Fusse eine feste Distanz unterhalb der Schulter einnehmen, die
vom Reibungskoeezienten an Fussen, Schulter und Rucken abhangen. Die minimalen Normalkrafte sind gerade dann so, dass der Kletterer nicht rutscht und die Reaktionswinkel gleich den
kritischen sind. Bei der tieferen Position der Fusse erfordert die Drehmomentenbedingung einen
grosseren Reaktionswinkel. Damit uberschreiten wir bei gleicher Normalkraft die kritischen
Werte, wir mussen also die Normalkraft erhohen. Bei einer hoheren Position der Fusse nden
wir kleinere Reibung an den Fussen und grossere Reibung an den Schultern, und erreichen damit
die optimalen Position fur den kritischen Reaktionswinkel an den Schultern.
Mit ahnlichen U berlegungen lasst sich auch die optimale Ruheposition fur das Klettern in
der Spalte ermitteln (Abbildung 2.55). Beim Aufsteigen muss in beiden Fallen zuerst ein Bein
hochgezogen werden, und dann mit dem zweiten Bein Schub produziert werden. es erfordert
hohere Reibung am unteren Bein und grossere Chance zum Ausrutschen. Der obere Fuss kann
aber die Sicherung ubernehmen.
Beim Aufstieg wird Arbeit geleistet und biochemische Energie zum Teil in potentielle Energie verwandelt. Weil Reibungskrafte keine konservativen Krafte sind, kann der Energiesatz
der Mechanik nicht angewendet werden. Fur die Energiebilanz muss nicht nur die gewonnene
potentielle Energie berucksichtigt werden, sondern auch die bei der Reibung auftretende Energieumwandlung in Warme bei der Erwarmung von Schultern, Handen, Felsen und Stein. Da
2.100
es sich um eine bewegliches System handelt, lasst sich die Arbeit auch nicht aus den ausseren
Kraften und dem vom Schwerpunkt zuruckgelegten Weg berechnen, die inneren Krafte ergeben
hier auch Beitrage zur Arbeit.
Spalt
Punkt mit
Drehmoment:0
Normalkraft
NFP
Reibung
Blick von oben
Gewicht
Normalkraft
N
Abbildung 2.55: Klettern an einer Spalte. Links: Von der Seite gesehen. Rechts: Von oben
gesehen (fur die Bezeichnung der Krafte siehe Abbildung 2.52).
Hochsprung: Sehr schematisch zeigt Abbildung 2.56 einen Hochspringer in der Absprung-
phase. Mit seinen Muskeln erzeugt der Springer innere Krafte, die wiederum beschleunigende
Reaktionskrafte des Bodens auf seine Fusse, in diesem Fall in erster Linie Normalkrafte, bewirken. Ist die Normalkraft grosser als das Gewicht, so ist beim Abheben eine Anfangsgeschwindigkeit vorhanden, die es erlaubt eine gewisse Hohe uber dem Boden zu erreichen. Beim Abheben
hat der Springer eine kinetische Energie T = mv 2 =2, die vor dem Absprung nicht vorhanden
war. Welche Kraft ist nun fur die Arbeit verantwortlich, die fur die A nderung der kinetischen
Energie notwendig ist. Die Normalkraft greift immer am gleichen Punkt des Korpers an, d. h.
es gilt d~r = 0 und damit dW = 0. Die Arbeit muss also von den inneren Kraften geleistet
werden. Ohne genaue Kenntnisse der physiologischen Zusammenhange konnen wir die inneren
Krafte und deren Angrispunkte nicht bestimmen, d. h. die Arbeit auch nicht berechnen. Wir
konnen lediglich den Anteil abschatzen, der notwendig ist, um den Schwerpunkt des Korpers
um die Hohe h zu verschieben:
2
W1!2 = F~ d~r = M2 (v 2 2 ; 0) = (N ; G)dz
2 : Abheben
0
1
W1!2 ist die Arbeit, welche die resultierende Kraft bei der Verschiebung des Schwerpunkts
leistet, Mv 2 2 =2 ist die A nderung der kinetischen Energie der Schwerpunktsbewegung.
Zwar konnen wir die Arbeit, die in den Relativbewegungen des Systems steckt, nicht ermitteln, gewisse Schlusse konnen wir jedoch ziehen. Die Arbeit ist z. B. umso grosser je grosser
N ist, und desto kleiner, je kleiner h ist. Dies ist u. a. der Grund dafur, dass der \Fosbury
Flop" zu grosseren Sprunghohen fuhrte als das konventionelle Rollen uber die Latte. Durch
den extrem gekrummten Rucken gelingt es dem Springer, selbst beim U berqueren der Latte den
Schwerpunkt seines Korpers unter der Lattenhohe zu halten.
Z
Z
S
h
s
S
S
2.101
G
N
G
Abbildung 2.56: Links: Hochspringer bei der Vorbereitung des Absprungs jN~ j > jG~ j; j~vj 0.
Mitte: Hochspringer kurz nach dem Abheben vom Boden jN~ j = 0; j~vj > 0. Rechts: Position des
Schwerpunkts beim \Fosbury Flop".
Stabhochsprung: In der Anlaufsphase erreicht
ein Stabhochspringer wie auch der Hochspringer
kinetische Energie. Dies geschieht durch Muskelarbeit, d. h. auch hier werden durch innere
Krafte Normal- und Reibungskrafte erzeugt, die
zur Beschleunigung fuhren. Die maximale kinetische Energie durfte etwa mit einer Geschwindigkeit um 10 m/s erreicht werden, etwa der eines
100 m Laufers. Konnte man in der Absprungphase diese gesamte kinetische Energie der Horizontalbewegung in eine solche der Vertikalbewegung
umsetzen, dann wurde der Springer eine Hohe von
h = v 2=2g 5 m erreichen konnen. Beim Stabhochspringen (siehe Abbildung 2.57), insbesondere wenn ein moderner hochexibler Stab verwendet wird, ist die Ezienz dieser Umwandlung besonders gut. Man sieht deutlich, dass die
kinetische Energie zunachst in elastische Deformationsenergie des Stabs verwandelt wird. Diese wird dann wieder verwendet um aufwarts gerichtete Geschwindigkeit zu erreichen, die zum
uberwinden der grossen Hohe notwendig ist.
Abbildung 2.57: Absprungphase beim Stabhochsprung.
2.102
Beim Einstecken des Stabs treten wieder Normal- und Reibungskrafte auf, die zum A ndern
des Geschwindigkeitsvektors notwendig sind. Am hochsten Punkt ist der Stab gestreckt, der
Athlet nahezu in Ruhe, die gesamte Energie ist nun in Form von potentieller Energie im Schwerefeld der Erde vorhanden. Beim Fallen gewinnt der Springer wieder kinetische Energie. Der
Stabhochsprungweltrekord von 4.77 m Hohe, der 1942 mit einem relativ steifen Bambusstab von
Cornelius Warnerdam aufgestellt wurde, bestand 17 Jahre. Erst als man dann uber Aluminium
und Stahlstabe schliesslich zum heute verwendeten Glasberstab uberging sprang der Rekord
auf 5.18 m und kletterte dann sukzessive auf uber 6 m. Beim Hochsprung ist die elastische Deformierbarkeit von Schuhsohlen und Gelenken oenbar zu klein, um einen grosseren Bruchteil
der horizontalen Geschwindigkeit in vertikale umsetzen zu konnen, die Anlaufgeschwindigkeit
ist daher auch oensichtlich viel kleiner als beim Stabhochsprung.
2.7.5.2 Stosse
Bei Stossen zweier Korper bleibt der Impuls erhalten, wenn wir die aussern Krafte als verschwindend klein betrachten. Fur die Frage der Energieerhaltung spielen aber auch die inneren
Krafte eine Rolle.
Ein Stoss heisst elastisch, wenn die Energie erhalten ist. Die inneren Krafte mussen konservativ sein, z. B. dem Federgesetz gehorchen. Die Deformation ist reversibel. Im eindimensionalen
Fall (zentraler Stoss) gelten dann Impuls{ und Energieerhaltung
m1v12 + m2v22 = m1v102 + m2v202 = E
m1v1 + m2v2 = m1v10 + m2v20 = p
2
2
2
2
Die Grossen v; v 0 und p stehen hier fur die x-Komponenten. Sind die Massen und die An-
fangsgeschwindigkeiten bekannt, so lassen sich die Endgeschwindigkeiten berechnen. Speziell
gilt:
i) Fur gleiche Massen m1 = m2: v10 = v2; v20 = v1 . Die Massen tauschen ihren Impuls aus.
ii) Fur m2 >> m1 , z. B. Stoss von m1 mit einer Wand m2, wobei v1 >> v2 ist:
v10 2v2 ; v1 ;v1 ; v20 v2
Die Masse m1 erfahrt eine grosse Impulsanderung, da ihre Geschwindigkeit das Vorzeichen
wechselt (nur die Betrage bleiben etwa gleich). Gleich gross ist die Impulsanderung der
Wand, doch ihre Geschwindigkeit andert kaum. Man beachte, dass bei bewegter Wand
(v2 6= 0) auch der Impulsbetrag von m1 geandert wird. Er wird verkleinert fur v2 in
Richtung von v1, und vergrossert fur v2 in Gegenrichtung von v1 .
Wir nennen einen Stoss vollstandig inelastisch, wenn die beiden Massen nach dem Stoss
dieselbe Geschwindigkeit haben, d. h. v10 = v20 = v 0. Aus der Impulserhaltung ist die Endgeschwindigkeit, wieder fur den eindimensionalen Fall, eindeutig bestimmt:
+ m2v2 :
v0 = m1mv1 +
m2
1
Die Energie ist jedoch nicht erhalten, denn die Rechnung zeigt, dass die kinetische Energie nach
dem Stoss kleiner ist als vorher. Der fehlende Teil ist in Warme umgewandelt worden. Nur
wenn wir diese auch als eine Form von Energie betrachten, ist die Gesamtenergie nach wie vor
erhalten.
2.103