Markovprozesse und Warteschlangensysteme

Markovprozesse und Warteschlangensysteme
M. Gruber
WS 2008/09
Inhaltsverzeichnis
1 Erneuerungsprozesse
3
2 Das elementare Erneuerungstheorem
6
1.1
1.2
1.3
2.1
2.2
2.3
Grundlegende Zufallsvariablen . . . . . . . . . . . . . . . . . . . . . . . . .
Faltung von Verteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
n-fache Faltung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Die Erneuerungsfunktion m(t) . . . . . . . . . . . . . . . . . . . . . . . . .
Erneurungsepochen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Einige Grenzwerte . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 Kostenmodelle
3.1
3.2
3.3
3.4
3.5
3.6
3.7
Einnahmen und Kosten . . . . . . . . . . .
Alterserneuerung . . . . . . . . . . . . . . .
Partielle Einnahme und Einnahmenrate . .
Alternierender Erneuerungsprozess . . . . .
Grenzverteilung für den Exzess . . . . . . .
Beobachtung des Exzess Y (t) . . . . . . . .
Beobachtung des Zeitspanne (spread) X (t)
4 Der Poissonprozess f(t) j t tg
4.1
4.2
4.3
4.4
Denitionen, Eigenschaften . .
Weitere Eigenschaften . . . . .
Ein Beispiel mit Stoppzeiten .
Stoppzeiten für Poissonprozesse
.
.
.
.
.
.
.
.
.
.
.
.
5 Markovketten
5.1
5.2
5.3
5.4
5.5
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Markovletten, Übergangswahrscheinlichkeiten . . . . . . . . . .
Beispiel: Brand-Switching and Market-Share ([2], Example 3-1)
Verbindung zur Erneuerungstheorie . . . . . . . . . . . . . . .
Kommunikationsklassen, Klasseneigenschaften . . . . . . . . . .
Endliche Kommunikationsklassen . . . . . . . . . . . . . . . . .
1
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
5
6
6
7
9
9
10
10
11
12
13
16
18
18
20
22
23
25
25
26
27
29
33
WS 2008/09
5.6
5.7
5.8
Markovprozesse und Warteschlangensysteme
Stoppzeiten, Starke Markoveigenschaft . . . . . . . . . . . . . . . . . . . . . 34
Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
Mean hitting times . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
6 Warteschlangentheorie
6.1
6.2
2
Der Satz von Little . . . . . . . . . . . . . . . . . . . . . . .
6.1.1 Bezeichnungen . . . . . . . . . . . . . . . . . . . . .
6.1.2 Durchschnittszeiten . . . . . . . . . . . . . . . . . .
6.1.3 Kunden-Zählprozesse . . . . . . . . . . . . . . . . . .
6.1.4 Grenzwerte der Kunden-Zählprozesse . . . . . . . .
6.1.5 Ankunfts- und Austritts-Zählprozesse, Ankunftsrate
6.1.6 Satz von Little . . . . . . . . . . . . . . . . . . . . .
M=M=1-Warteschlangen . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
38
38
38
38
38
39
39
39
40
WS 2008/09
Markovprozesse und Warteschlangensysteme
3
1 Erneuerungsprozesse
1.1 Grundlegende Zufallsvariablen
1. Wir betrachten den Zeitraum
T = [0; 1[. Epochen sind Zeitpunkte im Zeitraum T .
2. Wir betrachten Erneuerungsprozesse (z.B. Ankünfte von Bussen an einer Bushaltestelle). Die n-te Erneuerung ist eine Zufallsvariable Zn mit Werten in T . Wir
vereinbaren Z0 = 0.
3. Die Zwischenankunftszeit zwischen der (n 1)-ten und n-ten Ankunft ist eine Zufallsvariable Xn mit nichtnegativen Werten. X1 ist die erste Zwischenankunftszeit
(es gibt kein X0 ).
4. Der Prozess fZn j n 2 Ng heiÿt Erneuerungsprozess. Er hängt mit den Zwischenankunftszeiten zusammen:
X
Zn =
5. Wir nehmen an:
1j n
Xj :
X1 ; X2 ; X3 ; : : : sind stochastisch unabhängig.
6. Wir nehmen an: X2 ; X3 ; : : : sind identisch verteilt (X1 darf abweichend verteilt sein;
das vereinfacht in manchen Situationen das Rechnen).
7. Zugehörige Verteilungsfunktionen:
P (X1 t) =: A(t); t 2 T
P (Xj t) =: F (t); t 2 T; j = 2; 3; : : : :
8. Wenn F (0) > 0 ist, ist P (Xj
dann denieren
(1)
(2)
> 0) > 0 und der Erwartungswert EXj > 0; wir können
:= 1=EXj ; j = 2; 3; : : :
(3)
Die Bedeutung von werden wir bald kennen lernen; ist die durchschnittliche
Anzahl von Erneuerungen pro Zeiteinheit (Erneuerungsrate).
1.2 Faltung von Verteilungen
Wenn man die Verteilungen von Zufallsvariablen kennt, kennt man dann auch die Verteilungen ihrer Summe? Antwort: Faltung der Verteilungen.
Z2 = X1 + X2 .
Nehmen wir zunächst an, dass X1 und X2 diskrete Werte annehmen: P (X1 = i) =
P
P
ai 0 mit i2N ai = 1 und P (X2 = i) = fi 0 mit i2N fi = 1.
1. Uns interessiert z.B. die Verteilung von
WS 2008/09
Markovprozesse und Warteschlangensysteme
P (Z2 t) =
=
=
=
=
X
k t
X
k t
X
k t
X
k t
X
k t
P (X2 = k; X1 + X2 t)
(4)
P (X2 = k; X1 t
(5)
k)
P (X2 = k)P (X1 t
P (X2 = k)A(t
A(t
k)
k)
k)fk
(6)
(7)
(8)
=: (A F )(t):
(9)
In (6) wurde die stochastische Unabhängigkeit von
(9) deniert die Faltung von
4
X1 und X2 benutzt.
A und F .
2. Überlegen Sie, warum folgende Gleichheit gilt:
(A F )(t) = (F A)(t):
(10)
3. Nehmen wir nun an, dass X1 und X2 Werte in einem Kontinuum annehmen. Genauer: Die Verteilungsfunktion A sei dierenzierbar und es gelte A0 (t) = a(t); a ist
die Dichte(funktion) zu A. Analog sei f die Dichte zu F .
Die Faltung
A F = F A hat dann folgende Formen:
P (Z2 t) =
=
In diesem Fall hat
Z t
0
Z t
0
A(t
u)f (u) du
(11)
F (t
u)a(u) du:
(12)
A F = F A auch eine Dichte. Sie hat die Formen
d
dt P (Z2
t) =
=
Man bezeichnet sie mit
Z t
0
Z t
a f oder f a.
0
a(t
u)f (u) du
(13)
f (t
u)a(u) du:
(14)
Bei der Dierentiation z.B. von (11) nach t muss man nur den Integranden A(t
u)f (u) nach t dierenzieren; die Grenzen des Integrationsbereichs spielen nicht mit,
weil auÿerhalb des Integrationsbereichs der Integrand sowieso 0 ist.
WS 2008/09
Markovprozesse und Warteschlangensysteme
5
1.3 n-fache Faltung
1.
F 2 (t) := (F F )(t)
F n (t) := (F (n 1) F )(t)
f n (t) := dtd F n (t):
2. Die Verteilung von
(15)
(16)
(17)
Zn = X1 + (X2 + : : : + Xn ) ist
P (Zn t) := A F (n
1) :
(18)
WS 2008/09
Markovprozesse und Warteschlangensysteme
6
2 Das elementare Erneuerungstheorem
2.1 Die Erneuerungsfunktion m(t)
1. Wir führen eine weitere Zufallsvariable ein:
bis zur Epoche t; formal:
M (t) sei die Anzahl der Erneuerungen
M (t) := maxfn 0 j Zn tg:
2. Falls
(19)
X1 > t ist, ist M (t) = 0, denn Z0 = 0.
3. Der Prozess fM (t) j t
vom diskreten Prozess
4.
0g ist kontinuierlich und hat ganzzahlige Werte. Er wird
fXn j n = 1; 2; : : :g erzeugt, der Werte im Kontinuum hat.
Es gilt M (t) j , Zj t, also ist
P (M (t) j ) = P (Zj t) = (A F (j 1) )(t):
(20)
5. Wir interessieren uns für die Erwartungswerte m(t) := EM (t). m(t) heiÿt Erneuerungsfunktion (renewal function). Um sie zu berechnen, führen wir die Zufallsvariablen
(
Ij (t) :=
1
0
falls Zj
sonst
t
j = 1; 2; : : :
(21)
ein; es ist
M (t) =
X
1j<1
Ij (t);
(22)
also ist
m(t) = E
=
=
X
Ij (t)
(23)
EIj (t)
(24)
1j<1
X
1j<1
X
(A F (j
1j<1
1) )(t):
(25)
2.2 Erneurungsepochen
Mit
M (t) lassen sich wichtige neue zufällige Gröÿen ausdrücken.
1. Die Zuvallsvariable
ZM (t) =
X
1j M (t)
ist die letzte (jüngste) Erneuerungsepoche vor t.
Xj
(26)
WS 2008/09
Markovprozesse und Warteschlangensysteme
7
2. Die Zufallsvariable
ZM (t)+1 =
X
1j M (t)+1
Xj
(27)
ist die erste Erneuerungsepoche nach t.
3. Die Zufallsvariable
Y (t) = ZM (t)+1
ist der Exzess (excess). (Wieviele Minuten nach
t
(28)
t kommt der nächste Bus?)
4. Die Zufallsvariable
U (t) = t
ist das Alter (age). (Wieviele Minuten vor
ZM (t)
(29)
t kam der letzte Bus?)
5. Die Zufallsvariable
X (t) = Y (t) + U (t)
(30)
ist die Spanne (spread).
2.3 Einige Grenzwerte
Erinnerung:
Satz 1 (Starkes Gesetz der groÿen Zahlen) Sind Zufallsvariablen V1 ; V2 ; : : : identisch verteilt mit endlichem Erwartungswert und endlicher Varianz, dann gilt
1
P (nlim
!1 n
P
(Konvergenz n1 1in Vi
Wir nehmen nun 0 < EXj
Var Xj < 1 für alle j .
X
1in
Vi = EV1 ) = 1:
(31)
! EV1 fast sicher.)
< 1 für alle j an; es ist dann auch 0 < < 1. Ferner sei
1. Es gilt
P ( lim M (t) = 1) = 1:
t!1
Beweis Zu jedem j
ist
M (t) j .
2 N kann man t 2 T
wählen, so dass
Zj = X1 + : : : + Xj
(32)
t ist; dann
2. Es gilt
P (nlim
!1 Zn =n = 1=) = 1
Beweis Nach Satz 1 ist P (limn!1 n1 (Zn
1
n ( Zn
X1 + Xn+1 ) und n1 Zn sind gleich.
(33)
X1 + Xn+1 ) = 1=) = 1; die Grenzwerte von
WS 2008/09
Markovprozesse und Warteschlangensysteme
8
3. Es gilt
P ( lim ZM (t) =M (t) = 1=) = 1:
t!1
(34)
Beweis Aus (32) und (33) folgt P (limn!1 Zn =n = 1= ^ limt!1 M (t) =
1) = 1 (es
P (A ^ B ); im Spezialfall P (A) = P (B ) = 1 ist
P (A _ B ) = P (A) + P (B )
P (A ^ B ) = 1).
gilt immer
4. Es gilt
P ( lim M (t)=(M (t) + 1) = 1) = 1:
t!1
Beweis M (t) ! 1 fast sicher
) M (t)=(M (t) + 1) ! 1 fast sicher.
(35)
5. Es gilt
P ( lim ZM (t) =ZM (t)+1 = 1) = 1:
t!1
Beweis Wegen (34) gilt (ZM (t) =M (t))=(ZM (t)+1 =(M (t) + 1)
mit (35)
ZM (t) =ZM (t)+1 ! 1 fast sicher.
(36)
! 1 fast sicher; hieraus folgt
6. Es gilt
P ( lim ZM (t) =t = 1) = 1:
t!1
Beweis Folgt aus ZM (t) =ZM (t)+1 ZM (t) =t 1 und (36).
(37)
Satz 2 (Elementarer Erneuerungssatz)
Zufallsvariablen-Version:
P ( lim M (t)=t = ) = 1:
t!1
(38)
Erwartungswert-Version:
lim m(t)=t = :
(39)
t!1
Beweis Wir zeigen (38) für den Fall > 0:
M (t)=t = ZM (t) =t
#
#
1
mit (37)
M (t)=ZM (t)
#
mit (34)
Der Beweis der Erwartungswert-Version ist technisch schwieriger.
WS 2008/09
Markovprozesse und Warteschlangensysteme
9
3 Kostenmodelle
3.1 Einnahmen und Kosten
1. Die Zufallsvariablen Rj ; j = 1; 2; : : : sollen für Einnahmen (rewards) stehen, die den
Xj zugeordnet sind. Sie können positive und negative Werte annehmen. Negative
Einnahmen sind Kosten. Der Prozess fRj j j = 1; 2; : : :g bestehe aus unabhängigen,
identisch verteilten Zufallsvariablen. Jedes Rj darf von Xj abhängen, soll aber unabhängig von fXi j i 6= j g sein. Die Erwartungswerte EjRj j und EXj sollen existieren,
d.h. sie sollen endlich sein.
2. Der Prozess der kumulierten Einnahmen (cumulative reward) ist
C (t) =
X
1j M (t)
Rj
(40)
Rj fällt jeweils am Ende des Zeitraumes Xj an).
(wir nehmen an, die Einnahmen
Die erwartete kumulierte Einnahme für den Zeitraum
[0; t[ ist
c(t) = EC (t):
(41)
3. Wir interessieren uns für die durchschnittliche Einnahme pro Zeiteinheit
lim C (t)=t bzw.
t!1
lim c(t)=t:
t!1
Für sie gilt der
Satz 3 (Renewal-Reward-Theorem)
Zufallsvariablen-Version:
P ( lim C (t)=t = ERj =EXj ) = 1
t!1
(42)
Erwartungswert-Version:
lim c(t)=t = ERj =EXj
(43)
t!1
Beweis der Zufallsvariablen-Version
C (t)=t =
P
1j M (t) Rj =M (t)
#
ERj
Starkes Gesetz der groÿen Zahlen
M (t)=t
#
Elementarer Erneuerungssatz
WS 2008/09
Markovprozesse und Warteschlangensysteme
10
3.2 Alterserneuerung
[2], Example 2-1 (age replacement policies).
1. Die Zufallsvariablen Vj bezeichne die Lebensdauer des j -ten Exemplares einer Komponente (Chip, Glühbirne). Spätestens nach Ablauf der Zeit Vj muss es durch ein
(j +1)-tes Exemplar ersetzt werden. Es kann kostengünstiger sein, das j -te Exemplar
nach einer bestimmten Zeitspanne T auf jeden Fall gegen das (j + 1)-te Exemplar
auszuwechseln. Seien cf die Kosten für die Ersetzung einer der Komponente im Fehlerfall, cr die Kosten für die Ersetzung der Komponente nach der festen Zeit T und
es sei cr < cf .
2. Wir haben folgende Erneuerungs-Situation:
Xj = minfVj ; T g
(
cr Vj > T
Rj =
cf Vj T
k(T ) : = ERj =EXj
(Kostenrate)
3. Für welches
(44)
(45)
(46)
T ist die Kostenrate minimal?
= cf P (Vj T ) + cr P (Vj > T )
Z 1
@ P (X x) dx
EXj =
x @x
j
|
{z
}
1
ERj
=
Z T
0
=
=
=
Dichte von
@ P (X
x @x
j
Z T
0
Z T
0
Z T
0
P (Xj
(47)
(48)
Xj
x) dx
(49)
x) dx + T |P (Xj{z T })
(50)
=1
(1 P (Xj x)) dx
(51)
P (Xj > x) dx;
(52)
somit ist
k (T ) =
cf P (Vj
T ) + cr P (Vj > T )
RT
0
P (Xj > x) dx
(53)
4. Übungsblatt 2 behandelt konkrete Fälle (Verteilung von Vj gegeben).
3.3 Partielle Einnahme und Einnahmenrate
1. Wir erweitern unser Modell durch kumulative Einnahmen- und Kostenströme N (t) 0 (negativ) und P (t) 0 (positiv), die C (t) für t 2 [M (t); M (t) + 1] nach unten
WS 2008/09
Markovprozesse und Warteschlangensysteme
11
bzw. oben in folgender Weise beschränken:
X
1j M (t)
Rj
N (t) C (t) X
1j M (t)
Rj + P (t):
(54)
Dabei sei
R(M (t) + 1) = P (M (t) + 1) N (M (t) + 1) :
(55)
Rj = Pj
(56)
|
{z
}
=:PM (t)+1
|
{z
}
=:NM (t)+1
Somit gilt
Nj für j = 1; 2; : : : :
Die Zufallsvariablen fPj j j = 1; 2; : : :g seien iid, d.h. unabhängig und identisch verteilt. Ebenso seien die Zufallsvariablen fNj j j = 1; 2; : : :g iid. die Erwartungswerte
sollen existieren: EPj < 1, ENj < 1.
2. Wir halten fest: das Renewal-Reward-Theorem gilt weiterhin (in der ZufallsvariablenVersion und in der Erwartungswert-Version). Wir werden davon gleich intensiv Gebrauch machen.
3.4 Alternierender Erneuerungsprozess
[2], Example 2-2 (the alternating renewal process).
1. Seien fXuj j j = 1; 2; : : :g iid und seien fXdj j j = 1; 2; : : :g iid. u steht für up, d
steht für down (man stelle sich Zustände einer Maschine vor). Die ZufallsvariablenFamilien fXuj j j = 1; 2; : : :g und fXdj j j = 1; 2; : : :g seien unabhängig. Den Bezug
zu den Zufallsvariablen fXj j j = 1; 2; : : :g stellt die Gleichung
Xj = Xuj + Xdj
(57)
her: Xj hat nun die Rolle eines Reparaturzyklus (repair cycle) mit zufälliger Länge.
2. Der alternierende Erneuerungsprozess
(
I (t) =
1
0
für
für
fI (t) j t 0g ist deniert durch
t 2 [ZM (t) ; ZM (t) + Xu;M (t) [
t 2 [ZM (t) + Xu;M (t) ; ZM (t) + Xu;M (t) + Xd;M (t) [
(58)
I (t) hat den Wert 1, falls zur Zeit t der Zustand up vorliegt und den Wert 0, falls
zur Zeit t der Zustand down vorliegt.
3. Als kumulativen Einnahmeprozess
C (t) denieren wir nun
C (t) :=
Z t
0
I (u) du:
(59)
WS 2008/09
Markovprozesse und Warteschlangensysteme
12
Er kumuliert die up-Zeiten (es gibt pro Zeiteinheit quasi 1 e für den Zustand up).
Die Einnahme pro Zyklus ist
Rj =
Z Zj
Zj 1
I (u) du = Xuj für j = 1; 2; : : : :
(60)
4. Wie groÿ ist der Anteil der up-Zeiten an der Gesamtzeit?
Die Antwort gibt der Erneuerungssatz:
lim C (t)=t = ERj =EXj
t!1
(61)
= EXuj =EXj :
(62)
3.5 Grenzverteilung für den Exzess
[2], Example 2-3 (limiting distribution of excess).
Wir interessieren uns für die beiden Grenzwerte
lim 1
t!1 t
Z t
0
P (Y (u) y ) du und lim 1t
t!1
Z t
0
Y (u) du:
Der erste ist eine Verteilungsfunktion (als Grenzwert von Verteilungsfunktionen) bezüglich
y . Er gibt die Verteilung der Exzesse im zeitlichen Mittel an. Der zweite Grenzwert stellt
den relativen Anteil der Exzesse an der Gesamtzeit dar.
1. Wir xieren
y 0 und denieren den Indikatorprozess
(
I (t) =
1
0
für
für
Y (t) y
:
Y (t) > y
(63)
2. Den kumulativen Einnahmeprozess denieren wir wieder als
C (t) =
Z t
0
I (u) du:
(64)
Die Einnahme pro Zyklus ist
Rj =
Z Zj
Zj 1
I (u) du = minfXj ; y g:
(65)
Für Zufallsvariablen dieses Typs kennen wir bereits den Erwartungswert:
ERj
=
Z y
0
P (Xj > x) dx:
(66)
Also gilt nach der Zufallsvariablen-Version des Renewal-Reward-Theorems
lim C (t)=t = ERj =EXj = t!1
Z y
0
P (Xj > x) dx:
(67)
WS 2008/09
3. Für
Markovprozesse und Warteschlangensysteme
13
c(t) = EC (t) haben wir
c(t) = E
=
=
Z t
Z t
0
Z t
0
I (u) du
(68)
EI (u) du
(69)
P (Y (u) y ) du:
(70)
0
4. Die Grenzwerte limt!1 C (t)=t und limt!1 c(t)=t sind (fast sicher) gleich (RenewalReward-Theorem); also gilt
lim 1
t!1 t
Z t
0
P (Y (u) y ) du = Z y
0
P (Xj > x) dx:
(71)
Auf der linken Seite haben wir einen Grenzwert von Verteilungsfunktionen. Der
Grenzwert von Verteilungsfunktionen ist wiederum eine Verteilungsfunktion. Wenn
die linke Seite eine Verteilungsfunktion darstellt, dann auch die rechte Seite. Die
rechte Seite ist das zeitliche Mittel eines Indikatorprozesses. Man weiÿ also, wie man
die Werte der Verteilungsfunktion in der Praxis ermitteln kann.
R
5. Um den Grenzwert limt!1 1t 0t Y (u) du zu berechnen, denieren wir C (t) und damit
Rj geeignet neu:
C (t) :=
Z t
0
Y (u) du;
(72)
folglich
Rj =
Die Pfade
Z Zj
Zj 1
Y (u) du:
(73)
Y (t) haben eine Sägezahnstruktur. Rj lässt sich also leicht berechnen:
Rj =
Z Zj
Zj 1
Y (u) du = Xj2 =2:
(74)
Also ist
lim 1
t!1 t
Z t
0
Y (u) du = ERj =EXj
= 2 EXj2 :
3.6 Beobachtung des Exzess Y (t)
1. Als Funktion von
y 0 ist die Wahrscheinlichkeit
P (Y (u) y )
(75)
(76)
WS 2008/09
Markovprozesse und Warteschlangensysteme
14
die Verteilungsfunktion des Exzess Y (u) für den Fall, dass der Exzess zur Zeit
beobachtet wird. Es handelt sich also um eine bedingte Verteilungsfunktion .
u
Die unbedingte Verteilungsfunktion für den Exzess bekommt man, wenn man die
Wahrscheinlichkeitsverteilung des Beobachtungszeitpunkts u berücksichtigt. Wenn
z.B. u auf ]0; t[ gleichverteilt ist, haben wir die Dichtefunktion u 7! 1t [0 < u < t]
und die unbedingte Verteilungsfunktion des Exzess lautet
korrigiert
Z
1
P (Y (u) y ) 1t [0 < u < t] du =
1
Z t
1
t 0
P (Y (u) y ) du:
(77)
In der letzten Vorlesung haben wir gesehen:
Z t
lim 1
t!1 t 0
P (Y (u) y ) du = Z y
0
P (Xj > x) dx:
(78)
Der Ausdruck auf der rechten Seite von (78) beschreibt also die Wahrscheinlichkeitsverteilung des Exzess, die zufällige Beobachter im Durchschnitt wahrnehmen.
Nennen wir diese Verteilungsfunktion Fe (e für equilibrium ).
F die Verteilungsfunktion der Xj und F c (x) die zu F komplementäre Funktion
x 7! 1 F (x), so gilt
2. Ist
Fe (y ) = =
=
Z y
Z0y
Z0
y
0
P (Xj > x) dx
(79)
1 P (Xj x) dx
(80)
F c (x) dx
(81)
Ist Xe eine nach Fe verteilte Zufallsvariable, so hat sie die Wahrscheinlichkeitsdichte
fe (y ) = Fe0 (y ) = F c (y ):
(82)
Xe beschreibt den durchschnittlichen Exzess, Fe seine Wahrscheinlichkeitsverteilung.
Xe ?
1
EXe =
xfe (x) dx
0Z
1
=
x(1 f (x)) dx
0
x=1
!
Z 1 2
x2 c x
=
F (x)
f (x) dx
+
2
0 2
x=0
3. Welchen Erwartungswert hat
Z
Der erste Summand in (85) ist 0, wenn
dieser Annahme ist
EXe
(83)
(84)
(85)
F c (x) für x ! 1 stark genug abfällt. Unter
= 2 EXj2 = 2 (Var Xj + (EXj )2 ):
(86)
WS 2008/09
Markovprozesse und Warteschlangensysteme
15
4. Wenn Xj mit Parameter exponentialverteilt ist, fällt F c (x) für x ! 1 tatsächlich
stark genug ab und (86) ist erfüllt. Auÿerdem ist dann EXj = 1 und Var Xj = ( 1 )2
und man hat
EXe = 2 (( 1 )2 + ( 1 )2 ) = 1 :
(87)
Das bedeutet EXj = EXe , d.h. der Exzess wird im Mittel als ebenso lang erlebt wie
die Zeitabstände Xj (Gedächtnislosigkeit der Exponentialverteilung).
5. Nehmen wir nun Xj konstant an. Dann muss P (Xj = 1 ) =
ist. Var Xj ist in diesem Fall 0. Gleichung (86) liefert dann
EXe
1 sein, weil EXj =
= 2 (0 + ( 1 )2 ) = 12 EXj :
(88)
Hier wird der Exzess im Mittel als halb so lang erlebt wie die Zeitabstände
6. Fakten zur Exponentialverteilung
1
Xj .
E ():
Dichte:
f (x) = [0 x]e
x :
F (x) = [0 x](1
e
(89)
Verteilungsfunktion:
x ):
(90)
F~ (s) = Ee sX
Z 1
=
e sx e x dx
0
Z 1
=
e x(s+) dx
0
x=1
= s+ e x(s+) (91)
Momenterzeugende Funktion:
=
x=0
s+ :
(92)
(93)
(94)
(95)
Momente:
F~ 0 (s) = EXe
F~ 0 (0) = EX
sX
= (s+)2 s=0
= 1 :
F~ 00 (s) = EX 2 e sX
F~ 00 (0) = EX 2
=
2 (s+)3
= 2( 1 )2 :
(96)
(97)
(98)
(99)
(100)
(101)
s=0
(102)
(103)
WS 2008/09
Markovprozesse und Warteschlangensysteme
16
Erwartungswert:
EX
= F~ 0 (0) = 1 :
(104)
Varianz:
Var X = EX 2 (EX )2
= F~ 00 (0) F~ 0 (0)2
= ( 1 )2 :
(105)
(106)
(107)
Gedächtnislosigkeit:
P (fX>t+sg^fX>tg)
P (X>t)
P (X>t+s)
= P (X>t)
c
= FF(ct(+t)s)
(t+s)
= e e t
= e s
P (X > t + s j X > t) =
= F c (s)
(108)
(109)
(110)
(111)
(112)
(113)
= P (X > s):
(114)
3.7 Beobachtung des Zeitspanne (spread) X (t)
X (t) = Xj mit j = M (t) + 1. fX (t) j t 0g ist ein stochastischer Prozess.
1.
Wir xieren
x 0 und denieren den alternierenden stochastischen Prozess
I (t) : = [X (t) x]
(115)
und die Einnahme (reward)
Z Zj
x]:
(116)
= E minfXj ; xg xP (Xj > x)
(117)
=
(118)
Rj : =
Zj 1
I (u) du = Xj [Xj
Es gilt
ERj
=
Z x
Z0x
P (Xj > u) du
1 P (Xj u) du xP (Xj > x)
0 Z
x
=x
xP (Xj > x)
0
= xF (x)
F (u) du
Z x
0
xP (Xj > x)
F (u) du:
(119)
(120)
(121)
WS 2008/09
Markovprozesse und Warteschlangensysteme
17
2.
Wir setzen wieder
C (t) =
=
=
X
1j M (t)+1
X
Rj
Z Zj
1j M (t)+1 Zj 1
Z Z
M (t)+1
0
I (u) du
(123)
I (u) du
0
Z t
(122)
(124)
I (u) du
(125)
und
c(t) = EC (t)
Z t
0
(126)
P (X (u) x) du:
(127)
3. Anwendung des Renewal-Reward-Theorems.
Z t
lim 1
t!1 t 0
P (X (u) x) du = lim c(tt)
t!1
= EEXRjj
(128)
(129)
= ERj
= xF (x)
: = Fs (x)
Z x
0
F (u) du
(130)
(131)
(132)
(s für spread ). Fs ist die von Beobachtern durchschnittlich wahrgenommenen Verteilung des spread .
4. Inspection paradox .
Fs0 (x) = fs0 (x)
= (F (x) + xf (x)
= xf (x):
(133)
F (x))
(134)
(135)
Interpretation: Beobachter nehmen längere Zeitspannen überproportional wahr.
Den Faktor
x in xf (x) nennt man length biasing (Längenverfälschung).
WS 2008/09
Markovprozesse und Warteschlangensysteme
18
4 Der Poissonprozess f(t) j t tg
4.1 Denitionen, Eigenschaften
1.
(t) 2 N0 : Anzahl Ankünfte in [0; t], Realisierung: t 7! (t; ! ), monoton wachsend.
Inkrement (Zunahme) in ]t; t + h]: (t + h) (t).
2. (P1) Ein Poissonprozess hat unabhängige Inkremente, d.h.
(t + h) (t) und (t0 + h0 ) (t0 ) sind unabhängig, falls ]t; t + h]\]t0 ; t0 + h0 ] = ;:
3. (P2) Wahrscheinlichkeitsverteilung der
(t):
9>0 8j2N0 P ((t) = j ) = e
t (t)j ;
j!
d.h. für jedes t hat (t) eine Poissonverteilung mit Erwartungswert t (Ankunftsrate
mal Intervall-Länge).
P ((0) = 0) = 1.
Damit folgt aus (P2): (t + h)
(0 + t) (0).
4. Aus (P1) folgt:
5. Wie sind die Inkremente
(t) und (t) sind unabhängig, denn (t) =
(t + h) (t) verteilt?
Zur Klärung vergleichen wir verschiedene momenterzeugende Funktionen. Momenterzeugende Funktionen identizieren Verteilungen.
Ez (t+h)
= Ez (t) z ((t+h) (t))
= Ez (t) Ez ((t+h) (t)) :
(136)
(137)
In (137) nutzen wir die Unabhängigkeit der Inkremente.
Ez (t)
=
X
zj e
t (t)j
j!
j 2N0
X (tz )j
= e t
j!
j 2N0
= e t etz
= et(z 1) :
(138)
(139)
(140)
(141)
Analog gilt
Ez (t+h)
= e(t+h)(z
1) :
(142)
Ez (t+h) (t)
= e(t+h)(z
= eh(z 1) :
1) t(z 1)
(143)
Folglich ist
(144)
WS 2008/09
Markovprozesse und Warteschlangensysteme
19
Vergleicht man (141) mit (144), erkennt man: in (141) hat man eine momenterzeugende Funktion einer poissonverteilten Zufallsvariable mit Erwartungswert t. Somit
liegt in (144) eine momenterzeugende Funktion einer poissonverteilten Zufallsvariable mit Erwartungswert h vor.
Kurz:
(t + h) (t) P (h)
Die Verteilung der Inkremente
(145)
(t + h) (t) hängt nicht von t ab.
Man sagt:
(P3) Die Inkremente
(t + h) (t) sind stationär.
6. Gibt es gleichzeitige Ankünfte? Nein!
lim 1 P ((t + h) (t) 2)
h!0 h
= lim h1 (1 P ((t + h) (t) = 0)
h!0
= lim h1 (1 e h he h )
h!0
= lim (e h + 2 he h e h )
h!0
(146)
P ((t + h)
(t) = 1))
(147)
(148)
(149)
=0
(150)
(P4) Ankünfte geschehen nacheinander (orderliness) :
lim 1 P ((t + h)
h!0 h
(t) 2) = 0:
(151)
7. (P5)
P ((t + h)
(t) = 1) h ;
(152)
genauer:
lim 1 P ((t + h)
h!0 h
(t) = 1) = lim h1 he
h!0
h
= :
(153)
,: Poisson (1.Def.).
Für Minimalisten/Puristen: (P1)+(P3)+(P4) ,: Poisson (2.Def.).
Es gilt nämlich: (P1)+(P2)+(P3)+(P4)+(P5) ) (P2) und (P3)+(P4) ) (P5).
f(t) j t 0g ist ein Ankunftsprozess. Die Ankunftsepochen 0 t1 t2 : : : mar-
8. Für Pragmatiker: (P1)+(P2)+(P3)+(P4)+(P5)
9.
kieren seine Sprungstellen. Wir studieren die Zwischenzeiten (inter-arrival-times) .
Wie sind sie verteilt?
Zwischenzeiten: 1
= t1 ; 2 = t2
t1 ; : : : :
WS 2008/09
Markovprozesse und Warteschlangensysteme
1 > t , (t) = 0, daher ist P (1 > t) = P ((t) = 0) = e
20
t , d.h.
1 E ():
(154)
Wie ist 2 verteilt?
P (2 > t ^ 1 2 [x; x + h])
P (1 2 [x; x + h])
P ((t + x + h) (x + h) = 0 ^ (x + h)
=
P ((x + h) (x) = 1)
P (2 > t j 1 2 [x; x + h]) =
=
P ((t + x + h)
(x + h) = 0)P ((x + h)
P ((x + h) (x) = 1)
= P ((t + x + h) (x + h) = 0)
= e t :
Folglich ist limh#0 P (2 > t j 1 2 [x; x + h]) = P (2 > t j 1
liest man ab: 2 ist unabhängig von 1 und verteilt wie 1 .
(155)
(x) = 1)
(156)
(x) = 1)
(157)
(158)
(159)
= x) = e
t . Davon
Vollständige Induktion liefert: fj j j 2 Ng ist eine Familie unabhängiger, mit
Parameter exponentialverteilter Zuvallsvariabler.
10. 3.Denition eines Poissonprozesses: Ein Poissonprozess ist ein Ankunftsprozess mit
exponentialverteilten Zwischenankunftszeiten. (Hierbei spielt (t) die Rolle von M (t)
und j die Rolle von Xj .)
4.2 Weitere Eigenschaften
(t) = n. Wie groÿ ist unter dieser Voraussetzung die Wahrscheinlichkeit für
(u) = x, wenn x 2 f0; 1; : : : ; ng und u 2 [0; t] ist?
1. Sei
Man hat
P ((u) = x ^ (t) = n) = P ((u) = x ^ (t) (u) = n x)
= P ((u) = x)P ((t) (u) = n x)
=e
(160)
(161)
u (u)x e (t u) ((t u))n x
x!
(n x)!
(162)
t (t)n ;
n!
(163)
und
P ((t) = n) = e
WS 2008/09
also ist
Markovprozesse und Warteschlangensysteme
21
P ((u) = x ^ (t) = n)
(t) = n
!
x
n u (t u)n x
=
x
tn
!
n u x
u n x
=
)
( ) (1
x
x t
P ((u) = x j (t) = n) =
(164)
(165)
(166)
Das Resultat hängt nicht von ab. Man kann das Resultat interpretieren als Wahrscheinlichkeit, bei n Versuchen x-mal Erfolg zu haben, wenn die Wahrscheinlichkeit
für einen Einzelerfolg ut ist. Die Wahrscheinlichkeit ut ist das Verhältnis der IntervallLängen.
2. t1 ist die erste Ankunftsepoche. Wie ist sie verteilt, wenn
(t) = 1 ist?
P (t1 u j (t) = 1) = P ((u) = 1 j (t) = 1)
!
1 u 1
u 0
=
( ) (1
)
1 t
t
u
= :
t
Interpretation: Unter der Bedingung, dass genau eine Ankunft in
ist die Ankunftszeit gleichverteilt auf [0; t].
(167)
(168)
(169)
[0; t] stattndet,
3. ([2], Example 2-7) Wir betrachten folgende Situation: Fahrgäste kommen an einem
Bahnhof an. Ihre Ankünfte stellen einen Poissonprozess mit Ankunftsrate dar.
Am Bahnhof kommen Züge an. Ihre Ankünfte bilden einen Ankunftsprozess mit
Zwischenankunftszeiten Xj , wobei P (Xj t) = F (t) ist. F ist eine nicht näher
spezizierte Verteilungsfunktion. Es gelte EXj = 1=.
Gesucht ist der Anteil der Fahrgäste, deren Wartezeit einen Wert y nicht überschreitet. Mit anderen Worten: Wir wollen wissen, wie sich die verschiedenen Wartezeiten
auf die Fahrgäste verteilen.
Sei Kj die Anzahl der Fahrgäste, die in der Zeit Xj ankommen. Sei Kj (y ) die Anzahl
der Fahrgäste, deren Wartezeit y nicht übersteigt.
Der bedingte Erwartungswert für
E(Kj
Kj unter der Bedingung Xj ist
j Xj ) = Xj :
(170)
Erwartungswerte bedingter Erwartungswerte stimmen mit den entsprechenden unbedingten Ertwartungswerten überein:
EKj
= E(E(Kj j Xj ))
= EKj
= EXj = :
(171)
(172)
(173)
WS 2008/09
Markovprozesse und Warteschlangensysteme
22
Xj y , so ist Kj (y ) = Kj und E(Kj (y ) j Xj ) = Xj .
Ist Xj > y , so ist Kj (y ) Kj und E(Kj (y ) j Xj ) = y .
Ist
Also ist
E(Kj (y )) = E min(Xj ; )
(174)
F c (x) dx:
(175)
=
Z y
0
Nun können wir den Anteil der Fahrgäste mit Wartezeit
P
lim
n!1
1j n Kj (y )
P
1j n Kj
y berechnen:
1P
1j n Kj (y )
n
= nlim
P
1
!1 n 1j n Kj
P
limn!1 n1 1j n Kj (y )
=
P
limn!1 n1 1j n Kj
=
(176)
(177)
EKj (y )
EKj
=
Z y
0
(178)
F c (x) dx =: Fe (y ):
(179)
Fe (y ) steht für die Gleichgewichtsverteilung (equilibrium distribution) von F .
4.3 Ein Beispiel mit Stoppzeiten
1. ([2], Example 2-9, Single-server-loss system) Eine Bedienungsstation (Server) kann
nur einen Kunden bedienen. Sie ist busy , wenn sie gerade einen Kunden bedient,
ansonsten idle . Kunden, die eintreen, während die Bedienstelle busy ist, gehen
verloren.
Sei Sj 0 die Bedienzeit des j -ten Kunden (verlorene Kunden werden nicht gezählt).
Die fSj j j = 1; 2; : : :g seien unabhängig und identisch verteilt. Sei G(t) = P (S t)
die Verteilungsfunktion für die Bedienzeiten. Es sei ESj = 1= mit 0 < < 1.
Die Ankünfte der Kunden sollen einen Poissonprozess mit Ankunftsrate
Der Exzess Y ist dann exponentialverteilt: Y (t) E ().
bilden.
2. Die Bedienstelle sei zu Beginn idle . Die Zeit bis zur ersten Ankunft sei . Es gilt
E ().
Während des Zeitintervalls [; + S1 [ ist die Bedienstelle busy , ab
wieder idle . Sei I2 die Dauer der der darauolgenden idle -Zeit.
+ S1 ist sie
Wie ist I2 verteilt? I2 ist ein randomisierter Exzess eines Poissonprozesses:
I2 = Y ( + S1 ):
Trotzdem (wir haben es diskutiert) ist I2
E (). I2 ist unabhängig von und S1.
WS 2008/09
Markovprozesse und Warteschlangensysteme
23
3. Seien Ij die idle -Zeiten vor Sj . Insbesondere ist I1 = . Der Prozess fIj ; Sj g ist ein
alternierender Erneuerungsprozess. wie wir ihn schon studiert haben. Er hat die
Zyklen Xj = Ij + Sj .
4. Sei fb der Anteil der Zeit, in der die Bedienstelle busy ist. Von den alternierenden
Erneuerungsprozessen wissen wir
fb =
ESj
EIj + ESj
1=
1= + 1=
=
:
+
=
(180)
(181)
(182)
Kj die Anzahl der Ankünfte innerhalb Sj ; wir wissen schon:
EKj = :
Sei nb die Anzahl verlorener Ankünfte pro Zeiteinheit:
=
EKj
=
:
nb =
EXj
1= + 1=
5. Sei
(nach Erneuerungstheorem).
Nb (t) die Anzahl der verlorenen Ankünfte bis zur Zeit t, so gilt
N (t)
nb = lim b :
t!1 t
6. Sei ab der Anteil der verlorenen Ankünfte (überhaupt):
N (t)
ab = lim b
t!1 (t)
N (t)=t
= lim b
t!1 (t)=t
lim
N (t)=t
= t!1 b
limt!1 (t)=t
nb
=
=
:
+
Ist
4.4 Stoppzeiten für Poissonprozesse
(183)
(184)
(185)
(186)
(187)
nicht sau-
Denition 1 Sei fSj j j = 1; 2; : : :g ein stochastischer Prozess, unabhängig von f(t) j ber, nacht 0g. ist eine Stoppzeit für f(t) j t 0g, wenn eine Zufallsvariable mit bessern!
folgender Eigenschaft ist: Jedes Ereignis f tg hängt nur von f(s) j 0 s tg und fSj j j = 1; 2; : : :g ab. Insbesondere ist es unabhängig von den zukünftigen
Entwicklungen f(s) (t) j t > sg.
WS 2008/09
Markovprozesse und Warteschlangensysteme
24
Satz 4 Sei eine Stoppzeit für einen Poissonprozess f(t) j t 0g mit Rate . Dann
ist f(t + ) ( ) j t 0g ein Poissonprozess mit Rate . Er ist unabhängig von
und f(t) j 0 t g. Insbesondere ist der Exzess Y ( ) exponentialverteilt mit
Parameter und unabhängig von und f(t) j 0 t g.
WS 2008/09
Markovprozesse und Warteschlangensysteme
25
5 Markovketten
5.1 Markovletten, Übergangswahrscheinlichkeiten
Sei
fXn j n 2 N0g eine Familie von Zufallsvariablen mit Werten in N0.
1. Markov-Eigenschaft:
8n2N0 8j2N0 P (Xn+1 j Xn; Xn 1; : : : ; X0) = P (Xn+1 j Xn):
(188)
Hat die Familie fXn j n 2 N0 g die Markov-Eigenschaft, so nennt man sie Markov-
Kette. Die Markov-Eigenschaft charakterisiert einen gedächtnislosen Prozess, der
sich an nichts auÿer an seinen jüngsten Zustand erinnert.
Wir nehmen ab jetzt an, dass die Markov-Eigenschaft gegeben ist.
2. Stationarität ist gegeben, wenn die Wahrscheinlichkeiten für den Übergang von Zustand i zu Zustand j nicht von n abhängen:
8n2N0
P (Xn+1 j Xn = i) =: pij
(189)
Die Matrix P := (pij ) heiÿt Übergangsmatrix; ihre Zeilen enthalten diskrete Wahrscheinlichkeitsverteilungen.
Wir nehmen ab jetzt an, dass Stationarität gegeben ist.
3. Bezeichnungen:
aj := P (X0 = j )
a := (a0 ; a1 ; : : :)
a(jn) := P (Xn = j )
a(n) := (a(0n) ; a(1n) ; : : :)
p(ijn)
P (n)
4. Es gilt
:= P (Xn = j j X0 = i)
(190)
(191)
(192)
(193)
(194)
:= (p(ijn) )
(195)
p(ijn+s) = P (Xn+s = j j X0 = i)
(196)
P (n) = P n .
Beweis
=
=
=
X
k
X
k
X
P (Xn+s = j; Xn = k j X0 = i)
(197)
P (Xn+s = j j Xn = k; X0 = i)P (Xn = k j X0 = i)
(198)
= j j Xn = k)P (Xn = k j X0 = i)
(199)
P (Xn+s
k
X (n) (s)
=
pik pkj
k
(200)
WS 2008/09
Markovprozesse und Warteschlangensysteme
26
Also ist
P (n+s) = P (n) P (s) ;
(201)
P (1) = P
P (2) = P 2 usw.
(202)
insbesondere
(203)
5. Beispiel: Zustand 0 steht für schlechtes
h
i Wetter, Zustand 1 für schönes Wetter.
3=4 1=4
Die Übergangsmatrix sei P = 1=2 1=2 . Sie hat folgende Bedeutung: Wenn heute
schlechtes Wetter ist, dann ist morgen mit Wahrscheinlichkeit 3=4 wieder schlechtes
Wetter usw.
Wenn heute schönes Wetter ist, mit welchen Wahrscheinlichkeiten ist übermorgen
schönes Wetter?
Mathematica 5.1 for Linux
Copyright 1988-2004 Wolfram Research, Inc.
-- Motif graphics initialized -In[1]:= P={{3/4,1/4},{1/2,1/2}};
In[2]:= P.P
11 5
5 3
Out[2]= {{--, --}, {-, -}}
16 16
8 8
Wenn heute schönes Wetter ist, ist mit Wahrscheinlichkeit
Wetter.
3=8 übermorgen schönes
5.2 Beispiel: Brand-Switching and Market-Share ([2], Example 3-1)
Xn ist der n-te Einkauf des Kunden. Xn = j bedeutet: der Kunde wählt bei seinem nten Einkauf die Marke j . fXn j n 2 N0 g sei Markovsch, d.h.: der Kunde hat ein kurzes
Gedächtnis und entscheidet nur auf der Grundlage seines letzten Einkaufs; die Einkäufe
davor ,vergisst er regelmäÿig.
Es wird etwas für die Vermartung von Marke j unternommen (z.B. Verbesserungen
des Service oder der Qualität), was zu einer gröÿeren Übergangswahrscheinlichkeit pjj
P
und zu einer Verminderung von i6=k pji führt. Wie wirkt sich diese Veränderung auf den
Marktanteil der Marke j aus? Wie modelliert man überhaupt den Marktanteil?
Wir denieren die Zufallsvariable
Inj = [Xn = j ]:
(204)
WS 2008/09
Markovprozesse und Warteschlangensysteme
Der Marktanteil der Marke
27
j ist
P
lim
n!1
1sn Isj
n
;
(205)
der Erwartungswert davon
P
lim
n!1
1sn EIsj
n
falls diese Grenzwerte existieren.
Wie berechnet man sie?
Nehmen wir an, es existieren für alle
P
j j
= nlim
!1
=: j > 0:
n
;
(206)
(207)
= 1.
a(n) = a(n
und a(n)
(s)
1sn aj
j die Grenzwerte
lim a(n)
n!1 j
Sei = (1 ; 2 ; : : :). Es gilt
Wegen
P
1) P
(208)
! gilt dann auch
= P:
(209)
Das gibt eine Möglichkeit, zu berechnen (Eigenvektor von P T zum Eigenwert 1).
(n)
Die j stimmen mit den Grenzwerten in (206) überein, denn mit aj ! j gilt auch
(Analysis!)
1
n
X
1sn
a(js) ! j :
(210)
P
Wenn die Erwartungwerte der Zufallsvariablen n1 1sn Isj gegen j konvergieren, konvergieren sie selbst punktweise fast sicher gegen j (Maÿtheorie, Majorisierte Konvergenz!). Damit ist der Grenzwert in (205) fast sicher gleich j .
5.3 Verbindung zur Erneuerungstheorie
Grundidee dieses Abschnitts: Eine Konsequenz von Markoveigenschaft und Stationarität
ist, dass die Zwischenzeiten (hier: die Anzahl der Übergänge) bis zur Rückkehr zu einem
Zustand unabhängig und identisch verteilt sind. Das stellt die Verbindung zur Erneuerungstheorie her.
1. Einige Denitionen, Begrie und Zusammenhänge:
WS 2008/09
Markovprozesse und Warteschlangensysteme
28
Die Wahrscheinlichkeit der ersten Ankunft in j (falls i 6= j ) bzw. der ersten Rückkehr
zu j (falls i = j ) sei
fij(n) := P (Xn = j; Xn
1
6= j; :::; X1 6= j j X0 = i);
n = 1; 2; : : : :
(211)
Die Zeit, die der Prozess benötigt, um von i nach j zu kommen, sei Tij .
Tij ist eine Zufallsvariable mit fij(n) als Wahrscheinlichkeitsverteilung:
fij(n) = P (Tij = n):
Die Wahrscheinlichkeit, von
fij :=
X
1n1
(212)
i ausgehend jemals j zu erreichen ist
fij(n) :
(213)
Zustände klassiziert man so:
j rekurrent :, fjj = 1
j transient :, fjj < 1:
Falls
(214)
(215)
j rekurrent ist, deniert man die zu erwartende Zeit für die Wiederkehr als
j := ETjj =
X
1n1
nfjj(n) 1:
(216)
und sagt
j positiv :, j rekurrent und j < 1;
j null , j rekurrent und j = 1:
Falls
(217)
(218)
j transient ist, bezeichnet man Tjj als defektiv und deniert j := 1.
h
a b ci
2. Ein Beispiel ([2], p.152): Sei P = 0 1 0 mit
001
zwischen den Zuständen 0,1 und 2.
abc > 0. P beschreibt die Übergänge
1 und 2 sind absorbierend.
(1)
(n)
Es gilt f11 = f22 = 1, f10 = f12 = f20 = f21 = 0, f00 = a, f00 = 0 für n > 1,
P
P
(n)
f00 = a, f01
= a(n 1) b = an 1 b, f01 = 1n an 1 b = b=(1 a), f02 = 1n an 1 c =
c=(1 a) und f01 + f02 = 1.
Zustände
3. Wie zählt man die Häugkeit der Besuche eines Zustands j ? Der Prozess starte in i.
d.h. X0 = i. Für die Zählung benutzen wir einen Ansatz, der sich schon mehrmals
bewährt hat. Wir führen folgende Zufallsvariablen ein:
Iij (n) := [Xn = j ]
X
Iij (k):
Mij (n) :=
1kn
(219)
(220)
WS 2008/09
Markovprozesse und Warteschlangensysteme
29
Mij (n) gibt an, wie oft der Zustand j bis zur Zeit n aufgesucht wurde.
fMij (n) j n = 1; 2; : : :g ist ein Erneuerungsprozess mit Anfangsverteilung ffij(n)g
(Wahrscheinlichkeitsverteilung der Zeit, nach der der Prozess fXn j n = 0; 1; : : :g
(n)
zum ersten Mal den Zustand j erreicht) und Zwischenzeiten-Verteilung ffjj g (Wahrscheinlichkeitsverteilung der Zeit, nach der der Prozess fXn j n = 0; 1; : : :g zum
ersten Mal wieder zum Zustand j zurückkehrt).
ffij(n)g spielt hier die Rolle der Anfangsverteilung A, ffjj(n)g die der Verteilung F .
Beide Verteilungen können defektiv sein, d.h. sie addieren sich möglicherweise nicht
zu 1 (d.h. fij < 1 und fjj < 1 sind möglich). Diese Möglichkeit betrachten wir hier
nicht weiter.
Es ist
(n)
EIij
= p(ijn)
(221)
und
mij (n) := EMij (n) =
X
1kn
p(ijk)
(222)
mij heiÿt j -Erneuerungsfunktion .
Anwendung des Elementaren Erneuerungstheorems (Erwartungswertversion) für den
Fall fij = 1 und fjj = 1 (Rekurrenz) liefert die zu erwartende Häugkeit, mit der
der Zustand j aufgesucht wird:
X
lim 1 m (n) = lim n1
p(ijk)
n!1 n ij
1kn
(223)
= 1=ETjj
(
= 1=j
(224)
= 0 falls j null ist
> 0 falls j positiv ist
(225)
5.4 Kommunikationsklassen, Klasseneigenschaften
Der Zustandsraum der Markovkette
1. Für Zustände
fXn j n = 0; 1; : : :g sei I N0.
i; j 2 I; i 6= j denieren wir
i ! j : , fij > 0
(226)
, es existiert n 2
i $ j : , i ! j und j ! i:
Für
(n)
N mit pij
> 0:
(227)
(228)
i ! j sagt man von i erreicht man j und für i $ j i und j kommunizieren.
WS 2008/09
Markovprozesse und Warteschlangensysteme
30
Man hat die Eigenschaften
i $ j ) j $ i (Symmetrie)
i $ j und j $ k ) i $ k (Transitivität)
(229)
(230)
und fügt (künstlich) hinzu
i $ i (Reexivität)
(231)
Die drei Eigenschaften Symmetrie, Transitivität und Reexivität denieren eine Beziehung, die man Äquivalenzrelation nennt.
Mit Äquivalenzrelationen deniert man sogenannte Äquivalenzklassen . In unserem
Falle sind diese Äquivalenzklassen (oder kurz: Klassen) so deniert:
[i] : = fj 2 I j i $ j g
(232)
Man nennt sie kommunizierende Klassen . Die kommunizierenden Klassen sind
entweder identisch oder disjunkt: Es gilt [i] = [j ] genau dann, wenn i $ j und
[i] \ [j ] = ; genau dann, wenn i 6$ j . Der Zustandsraum zerfällt somit in kommunizierende Klassen.
C eine beliebige Teilmenge des Zustandsraums I .
Wir sagen, C ist abgeschlossen , wenn C mit jedem Zustend i, den es enthält, auch
jeden Zustand j enthält, der von i aus erreichbar ist (i 2 C ^ i ! j ) j 2 C ).
C ist genau dann abgeschlossen, wenn für alle i 2 C und alle j 2= C gilt: pij = 0.
2. Sei
Wir sagen, eine Markovkette ist irreduzibel , wenn ihr Zustandsraum aus einer einzigen kommunizierenden Klasse besteht.
Wenn eine Markovkette irreduzibel ist, gibt es keine echte Teilmenge des Zustandsraums, die abgeschlossen ist.
3. Erinnerung: Ein Zustand
j ist
P
(n)
(n)
1n fjj = 1 und j = 1n nfjj
P
P
(n)
(n)
null, wenn fjj = 1n fjj = 1 und j = 1n nfjj =
P
(n)
transient, wenn fjj = 1n fjj < 1 ist.
positiv, wenn fjj
=
P
< 1 ist,
1 ist,
Kommunizierende Klassen einer Markovkette haben folgende schöne Eigenschaft:
Satz 5 (The Class Property Theorem) Die Zustände einer kommunizierenden Klasse A sind entweder alle positiv oder alle null oder alle transient.
Beweis
WS 2008/09
Markovprozesse und Warteschlangensysteme
31
A = fj g, d.h. einelementig ist, ist entweder fjj < 1 (dann ist j transient) oder
fjj = fjj(1) = 1 und damit j = 1 (dann ist j positiv).
(b) Für den langen Rest des Beweises enthalte A mindestens zwei verschiedene Elemente.
(a) Falls
(c) Es folgen einige Überlegungen, die schlieÿllich zu einer Charakterisierung von transient bzw. rekurrent führen.
Die Zufallsvariable Mij (n) gibt an, wie oft die Markovkette, die in i startet, innerhalb
der Epoche n den Zustand j aufsucht. Sei
Mij : = nlim
!1 Mij (n) 1:
(233)
Es gilt
P (Mij > 0) = fij :
(234)
und
P (Mij > k) = P (Mjj
= P (Mjj
= P (Mjj
= P (Mjj
= :::
= P (Mjj
= fjjk fij :
Wir wissen bereits, dass EMij
=
P
1 j Mij > 0)P (Mij > 0)
1 j X0 = j )fij
2 j Mjj > 0)fjj fij
2 j X0 = j )fjj fij
>k
>k
>k
>k
> 0)fjjk 1 fij
(235)
(236)
(237)
(238)
(239)
(240)
(241)
(k)
1k<1 pij gilt.
Andrerseits ist
EMij
=
=
=
=
=
=
=
=
Man sieht nun:
X
1k<1
kP (Mij = k)
X
X
1k<1 0r<k
X
P (Mij = k)
(243)
[r < k]P (Mij = k)
(244)
[r < k]P (Mij = k)
(245)
P (Mij = k)
(246)
X
1k<1 0r<1
X
X
0r<1 1k<1
X
X
0r<1 r<k<1
X
0r<1
X
0r<1
(242)
P (Mij > r)
(247)
fjjr fij
(248)
fij
:
1 fjj
(249)
WS 2008/09
Markovprozesse und Warteschlangensysteme
32
j rekurrent , P1k<1 p(jjk) = 1,
j transient , P1k<1 p(jjk) < 1,
i ! j und j rekurrent ) P1k<1 p(ijk) = 1,
i ! j und j transient ) P1k<1 p(ijk) < 1.
(d) Nun werden wir sehen, wie sich die Eigenschaften transient bzw. rekurrent von
auf k übertragen, wenn j $ k gilt.
Wenn
j
j und k kommunizieren, gibt es J; K mit
= p(jkJ ) > 0;
(250)
> 0;
(251)
so dass für alle
= p(kjK )
n gilt:
(J +n+K )
pjj
p(kkn) :
(252)
Summiert man (252) über n, sieht man, dass j und k nur entweder beide transient
(wenn die Summation einen endlichen Wert liefert) oder beide rekurrent (wenn sie
einen unendlichen Wert liefert) sein können.
(e) Wir untersuchen nun den transienten Fall weiter.
Wenn j null ist und k rekurrent, gilt (wir benutzen wieder (252))
X
lim 1
p(jjJ +m+K ) = 0 = 1=j
n!1 n
1mn
(253)
und damit auch
X
p(kkm) = 0 = 1=k ;
lim 1
n!1 n
1mn
also ist auch
(254)
k null.
Satz 6 Oene Kommunikationsklassen sind transient.
Beweis Sei A eine oene Kommunikationsklasse.
i 2 A; j 2= A mit pij > 0. Es ist fji = 0.
Zu zeigen ist: fii < 1.
Unter der Bedingung X0 = i gilt:
Wähle
fii = fji pij + P (Rückkehr zu i j X1 6= j )(1
|
{z
}
|{z}
=0
1
1 pij < 1:
pij )
(255)
(256)
WS 2008/09
Markovprozesse und Warteschlangensysteme
33
Folgerung 1 Rekurrente Klassen sind abgeschlossen.
4. Abgeschlossene Kommunikationsklassen können transient, null oder positiv sein (!
Übungsblatt 7).
5.5 Endliche Kommunikationsklassen
1. Wir betrachten nun endliche Kommunikationsklasse, d.h. solche, die nur endlich
viele Elemente enthalten.
Satz 7 Endliche abgeschlossene Kommunikationsklassen sind positiv.
Beweis Sei A eine endliche abgeschlossene Kommunikationsklasse.
(a) Da A abgeschlossen ist, kommt die Markovkette, wenn sie in i 2 A startet, nach
Übergängen sicher bei einem Zustand j 2 A an, d.h. für alle i 2 A und n 2 N gilt
X (n)
pij
j 2A
(b) Angenommen,
= 1:
n
(257)
j ist transient oder null. Dann ist für i 2 A mit i ! j
X
lim 1
p(ijk) = 0:
n!1 n
1kn
(258)
(c) Wir summieren (258) über j :
X
X
p(ijk)
lim 1
n!1 n
j 2A
1kn
X (k)
X
1
pij
= nlim
!1 j 2A n
1kn
X X (k)
1
= nlim
pij
n
!1
1kn j 2A
= 1 (Widerspruch!)
0=
Also kann
(259)
(260)
(261)
(262)
A nur positiv sein.
2. Eine Konsequenz der vorigen Überlegungen ist
Satz 8 Eine Markovkette mit endlichem Zustandsraum kann nur dann einen
transienten Zustand i haben, wenn ein j existiert mit i ! j aber j 6! i (d.h.
wenn es eine oene Kommunikationsklasse gibt).
WS 2008/09
Markovprozesse und Warteschlangensysteme
3. Beispiel:
2
34
3
0 0 0 0
6
7
60 0 1 0 0 07
6
7
60 0 0 0 7
6
7
P =6
7
60 0 0 07
6
7
4 0 0 0 0 5
0 1 0 0 0 0
steht für eine Zahl zwischen 0 und 1, die Zeilensummen von P sind 1.
A = f0; 1; 2; 3; 4; 5g.
[0] = f0; 4g ist oen, also transient.
[1] = f1; 2; 5g ist abgeschlossen und endlich, also positiv.
[3] = f3g ist oen, also transient.
5.6 Stoppzeiten, Starke Markoveigenschaft
1. Sei
A I . Wir denieren die Eintrezeit (hitting time) bei A als
H A : = inf fn 0 j Xn 2 Ag
(263)
inf ; = 1. H A ist eine Zufallsvariable.
H A (! ) nimmt für Pfade ! , die A nie treen, den Wert 1 an.
mit der Konvention
Sei
hAi : = Pi (H A < 1)
: = P (H A < 1 j X0 = i)
(264)
(265)
und
kiA : = Ei H A
X
: = nPi (H A = n) + 1Pi (H A = 1)
n
mit der Konvention
Ist
(266)
(267)
1 0 = 0.
A abgeschlossen, nennt man hAi auch Absorptionszeit.
Sei
hA : = (hAi )i2I
der Vektor der Eintrezeiten.
(268)
WS 2008/09
Markovprozesse und Warteschlangensysteme
35
Es gilt
hAi = 1 für i 2 A
X
hAi = hAj pij für i 2= A:
j 2I
(269)
(270)
Satz 9 hA ist die kleinste nichtnegative Lösung des Systems
hAi = 1
für i 2 A
P
Ap
hAi =
h
=A
j 2I j ij für i 2
" 1
0 0 0 #
1=2 0 1=2 0
2. Beispiel: P = 0 1=2 0 1=2 . In der Vorlesung gerechndet:
0 0 0 1
k2f1;4g = 2 (mittlere Absorptionszeit).
3.
hf24g = 1=3, hf14g = 0,
T : ! f0; 1; 2; : : :g [ f1g ist eine Stoppzeit zu fXn j n 2 N0 g, wenn gilt
fT = ng 2 F (X0; : : : ; Xn)
für alle
n 2 N0 :
Beispiele:
j 2 I , Tj = inf fn 1 j Xn = j g.
Tj ist eine Stoppzeit (rst passage time):
fT = ng = fX1 6= j; : : : ; Xn 1 6= j; Xn = j g 2 F (X0; : : : ; Xn).
(b) A I; H A = inf fn 0 j Xn 2 Ag.
H A ist eine Stoppzeit (rst hitting time):
fT = ng = fX0 2= A; : : : ; Xn 1 2= A; Xn 2 Ag 2 F (X0; : : : ; Xn).
(c) A I , LA = supfn 0 j Xn 2 Ag.
LA (last exit tiime) ist keine Stoppzeit!
(a)
4. Für eine Stoppzeit
T bezeichnet F (X0 ; : : : XT ) die -Algebra der Ereignisse B mit
B \ fT = mg 2 F (X0 ; : : : Xm ) für alle m:
Für
! 2 mit T (! ) < 1 interessiert typischerweise die Zufallsvariable
! 7! XT (!) (! );
die wir als
XT notieren.
Satz 10 (Starke Markoveigenschaft) Sei T eine Stoppzeit zum Markovprozess fXn j n 0g. Dann ist unter der Bedingung T < 1 und XT = i der
Prozess fXT +n j n 0g ebenfalls ein Markovprozess.
M.a.W.: Für B 2 F (X0 ; : : : ; XT ) gilt
P (fXT = j0 ; : : : ; XT +n = jn g \ B j T < 1; XT = i)
:
= Pi (X0 = j0 ; : : : ; Xn = jn )P (B j T < 1; XT = i)
Oft wird die Starke Markoveigenschaft mit
B = benutzt.
WS 2008/09
Markovprozesse und Warteschlangensysteme
36
5.7 Beispiele
1. Gambler's ruin, [1] Example 1.3.3
0 < p = 1 q < 1, p00 = 1, pi;i+1 = p und pi;i 1 = q für i = 1; 2; : : :.
Für die Ruinwahrscheinlichkeit hi = Pi (H f0g < 1) gilt
Seien
h0 = 1
hi = phi+1 + qhi
Es liegt eine lineare Rekursion vor.
Die charakteristische Gleichung x2
Im Fall
(271)
1
q
1
px + p
i = 1; 2; : : :
(272)
= 0 hat die Lösungen x 2 f pq ; 1g.
p 6= q (verschiedene Wurzeln) setzt man
hi = A + B ( pq )i
an und bestimmt
(273)
A und B .
Im Fall p < q ist das Casino im Vorteil. Da hi 1 für alle i gelten muss, muss B
sein. Daraus folgt A = 1 und hi = 1 für alle i, der sichere Ruin.
=0
Im Fall p > q ist der Spieler im Vorteil. Da h0 = 1 sein muss, ist A + B = 1. Also ist
hi = A + (1 A)( pq )i = ( pq )i + A(1 ( pq )i ). Man sieht, dass A 0 sein muss, denn
andernfalls gibt es negative Werte für gewisse hi . Wegen der Minimalitätseigenschaft
der hi folgt A = 0, also ist hi = ( pq )i .
Im Fall
p = q (Doppelwurzel 1) setzt man
hi = A + Bi
(274)
an (eigentlich: hi = A + Bi1i ) und bestimmt hieraus A und B . Wegen
folgt hier A = 1; B = 0, also hi = 1, also auch hier der sichere Ruin.
0 hi
1
2. Birth-and-death-chain, [1] Example 1.3.4
= qi 0 und pi;i+1 = pi 0 mit pi + qi = 1 für i = 1; 2; : : :.
Für hi = Pi (H f0g < 1) gilt
Seien pi;i 1
h0 = 1
hi = pi hi+1 + qi hi
Betrachte ui
= hi
1
(275)
1
i = 1; 2; : : : :
(276)
hi .
Aus
pi ui+1 = pi hi pi hi+1
qi ui = qi hi 1 qi hi
hi = pi hi+1 + qi hi
(277)
(278)
1
(279)
WS 2008/09
Markovprozesse und Warteschlangensysteme
37
folgt
pi ui+1 = qi ui
(280)
d.h.
ui+1 = pqii ui
q1
= pqii p1 u1
: = i u1
(281)
(282)
(283)
mit
0 = 1
1 = pq11
2 = pq22 qp11 usw.
(284)
(285)
(286)
Wegen
X
1k<i
uk = h0
hi (\teleskopischeSumme00 )
(287)
gilt
hi = 1
mit u1
u1
X
0k<i
k
(288)
0.
Zwei Fälle müssen nun unterschieden werden:
(a)
(b)
P
P
= 1: Dann muss u1 = 0 und damit hi = 1 sein.
P
k k < 1: Dann muss hi = 1 u1 0k<i k 0 und minimal sein.
k k
Dies ist für u1
= 1=
P
k k der Fall. Also ist hi
=
P
k
Pj i .
k k
5.8 Mean hitting times
Satz 11 ([1], Theorem 1.3.5) Sei kiA = Ei H A und kA = (kiA )i2I .
Dann ist kA die minimale nichtnegative Lösung des Systems
kiA = 0 für i 2 A
X
kiA = 1 +
kjA pij für i 2= A
j 2= A
(289)
(290)
WS 2008/09
Markovprozesse und Warteschlangensysteme
6 Warteschlangentheorie
6.1 Der Satz von Little
6.1.1 Bezeichnungen
Cj ; j = 1; 2; : : :
tj ; j = 0 ; 1 ; : : :
Tj = tj +1 tj
Dj ; j = 1; 2; : : :
Sj ; j = 1; 2; : : :
Wj = Dj + Sj
tj + Wj
Kunden (in der Reihenfolge ihres Eintreens)
Ankunftszeit des Kunden Cj (0 = t0 t1 : : : < 1)
Zwischenzeiten
Zeit, die Kunde Cj auf Bedienung wartet (in queue )
Bedienzeit für Kunde Cj (in service )
Zeit, die Kunde Cj im System verweilt
Austrittszeit des Kunden Cj aus dem System
Bemerkung 1 Alle Gröÿen sind zufällig.
6.1.2 Durchschnittszeiten
durchschnittliche Wartezeit (delay ) pro Kunde
X
lim 1
Dj =: d
n!1 n
1j n
durchschnittliche Bedienzeit pro Kunde
X
lim 1
Sj =:
n!1 n
1j n
1
( = Servicerate)
durchschnittliche Systemverweilzeit pro Kunde
X
lim 1
Wj =: w = d + 1
n!1 n
1j n
6.1.3 Kunden-Zählprozesse
# Kunden in queue :
Nq (t) =
X
1j 1
[tj t < tj + Dj ]
# Kunden in service :
Ns (t) =
X
1j 1
[tj + Dj t < tj + Wj ]
# Kunden im System:
N (t) = Nq (t) + Ns (t) =
X
1j 1
[tj t < tj + Wj ]
38
WS 2008/09
Markovprozesse und Warteschlangensysteme
39
6.1.4 Grenzwerte der Kunden-Zählprozesse
durchschnittliche # Kunden in queue :
Z t
lim 1
t!1 t
0
Nq (u) du =: Q
durchschnittliche # Kunden in service :
Z t
lim 1
t!1 t 0
Ns (u) du =: Ls
durchschnittliche # Kunden im System:
lim 1
t!1 t
Z t
0
N (u) du =: L = Q + Ls
6.1.5 Ankunfts- und Austritts-Zählprozesse, Ankunftsrate
# Ankünfte bis zur Zeit t:
(t) = maxfj j tj tg
# Austritte bis zur Zeit:
(t) = (t) N (t)
Ankunftsrate:
lim 1 (t) =: t!1 t
6.1.6 Satz von Little
Satz 12 Existieren die Grenzwerte und w und sind sie endlich, so gilt
L = w :
(291)
Existiert der Grenzwert d und ist er endlich, so gilt
Q = d :
(292)
Existiert der Grenzwert 1 und ist er endlich, so gilt
Ls = :
(293)
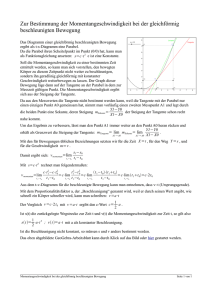
Beweis Kein echter Beweis, nurR eine Ideenskizze anhand der
in Abb. 1 gezeigten Situation.
RT
1
Für
j = 1; 2; 3; 4 ist Wj = 0 [tj
X
1j (T )
Wj =
=
X
u < tj + Wj ] du =
Z T
1j (T ) 0
Z T
X
0
[tj u < tj + Wj ] du, folglich
[tj u < tj + Wj ] du
[tj u < tj + Wj ] du =
0 1j (T )
(294)
Z T
0
N (u) du :
(295)
WS 2008/09
Markovprozesse und Warteschlangensysteme
40
Abbildung 1: Zum Beweis des Satzes von Little (aus [2], p.235); in der dargestellten
Situation ist N (t) = 2; N (T ) = 0; (T ) = 4.
Im allgemeinen Fall hat man
Z t
0
N (u) du =
X
1j Wj + o(t)
(296)
wobei der Nachweis des o(t)-Terms die Sache anspruchsvoll macht.
Rt
P
W
Aus (296) folgt 1t 0 N (u) du = 1t (t) 1j (t) (tj) + 1t o(t) und mit t ! 1 die Little-Formel.
6.2 M=M=1-Warteschlangen
(existiert nur handschriftlich)
Literatur
[1] J. R. Norris. Markov Chains. Cambridge University Press, rst edition, 1997.
[2] R. W. Wol. Stochastic Modeling and the Theory of Queues. Prentice Hall, 1989.