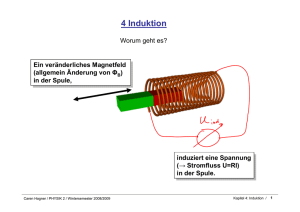
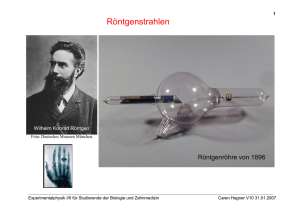
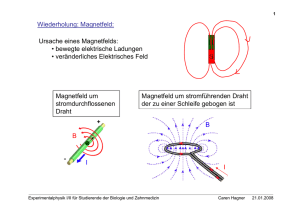
Prof. Dr. Caren Hagner

Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Prof. Dr. Caren Hagner
Borexino Experiment
(Gran Sasso, Italien)
Universität Hamburg
Institut für Experimentalphysik
Luruper Chaussee 149
22761 Hamburg
Email:
[email protected]
Büro:
DESY Gelände Bahrenfeld, Geb. 62, Zi. 210
Telefon:
040 8998 2297
Webseite: http://neutrino.desy.de/lehre/
Sprechstunden: nach Vereinbarung (email)
OPERA Experiment
(Neutrinooszillationen) am
Gran Sasso Untergrundlabor
(Italien)
Mein Forschungsgebiet: Neutrinophysik
(Elementarteilchenphysik, Astroteilchenphysik)
1
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Literaturhinweise: (nur einige Beispiele)
Haas: “Physik für Pharmazeuten und Mediziner”,
Wissenschaftliche Verlagsgesellschaft Stuttgart
 Harten: “Physik für Mediziner”,
Springer
 Hellenthal: “Physik für Mediziner und Biologen”,
Wissenschaftliche Verlagsgesellschaft Stuttgart
 Trautwein, Kreibig, Oberhausen: “Physik für Mediziner, Biologen, Pharmazeuten”,
de Gruyter

Skript von Dr. Salehi (hielt die Vorlesung in den letzten Jahren in HH):
außerdem viele Infos zur Vorlesung, Altklausuren etc.
http://wwwiexp.desy.de/users/uwe.holm/Zahnmedizin.html
Von diesen Vorlesungen (Salehi) gibt es auch Video Aufzeichnungen:
http://lecture2go.uni-hamburg.de/lecture/-/sv/zJ0DPvaBbYjc2lL2vi14GAxx
und http://lecture2go.uni-hamburg.de/lecture/-/sv/BQSWDLTMqN9Vukrbytua4Qxx
Passwort: salehi
2
Was ist Physik?
Φυσική
„Physike“ = Naturlehre
Platon
Aristoteles
Mikrokosmos
Makrokosmos
Struktur des Protons
Hubble Ultra Deep Field
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Ziel der Physik:
Quantitatives Verständnis der (unbelebten) Natur
Reduktion
Elementare Teilchen
Elementare Gesetze
Vorhersagen und Anwendungen
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Methode der Physik
Beobachtung
Experiment
Hypothese
induktiv
Gesetz, Theorie, Modell
deduktiv
Vorhersagen
Rate das Naturgesetz
Berechne die Auswirkungen
Vergleich mit dem Experiment
7
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Physikalische Größen: Maßzahl, Einheit und Fehler
Messung:
Vergleich einer physikalischen Größe mit einer Maßeinheit (Normal, Standard)
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
SI-Einheiten (SI = Système Internationale d’Unités)
(Wer mehr darüber wissen will: Geo 3/2008, „Über alle Maßen genau“,
Spektrum der Wissenschaft 3/2010 „Die Zukunft von Kilogramm & Co.“)
kg, s, m, A, K, mol, Cd
1 kg = Masse des internationalen Kilogrammprototyps aus Platin-Iridium
1 s = Das 9.192.631.770 fache der Periodendauer der Strahlung,
die beim Übergang der Hyperfeinstrukturniveaus des Grundzustandes
von 133Cs entsteht.
1 m = Länge der Strecke, die Licht im Vakuum in der Dauer von
1/299.792.458 Sekunden durchläuft.
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Der Kilogramm Prototyp
Bureau International des Poids et Mesures (BIPM) in Sèvres bei Paris.
In Deutschland verantwortlich:
Physikalisch Technische Bundesanstalt PTB in Braunschweig:
http://www.ptb.de/de/wegweiser/einheiten/si/
Das „Ur-Kilogramm“ liegt seit 1889 in Sevres.
weltweit gibt es ca. 80 Kopien,
1950 und 1990 Vergleich mit dem Original
Problem:
Die Masse des Urkilogramms nimmt ab!
Bisher ca. 50μg (durch Reinigung?)
An Neudefinition wird weltweit gearbeitet
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Einheit der Länge – Historie
Bis ins 18.Jhdt: Längeneinheit (Elle) war nur lokal definiert.
(z.B.Erfurt 40cm, dagegen München 80cm)
Wiener Tuch- und Leinen Elle
Um 1790 gibt es in Frankreich 250000 Maßeinheiten!
Elle am Rathaus von Celle
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Einheit der Länge – Meter
Danach Versuch globaler Definition (anfangs aus der Geometrie der Erde):
Idee: 1 Meter = 10 Millionster Teil des Erdmeridianquadranten durch Paris
1735 Expedition der Pariser Akademie nach Peru und Lappland.
1793 Festlegung der Längeneinheit Meter als 10 Millionster Teil des
Erdquadranten auf dem Meridian durch Paris.
1792-99 Bestimmung des Meridianbogens zwischen Dünkirchen und Barcelona
durch Delambre und Mechain.
12
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Expedition von Delambre und Mechain (1792-99) (Sehr lesenswert in Geo kompakt Nr.22)
Bestimmung der Entfernung zwischen Dünkirchen und Barcelona
Triangulation:
Sind 2 Winkel und eine Seitenlänge eines Dreiecks bekannt,
Lassen sich auch die anderen beiden Seiten berechnen
Auf Grund eines kleinen Fehlers in der Messung von Mechain gilt:
Länge des Erdmeridianquadranten = 10.001,966 km (statt 10.000 km)
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Einheit der Länge – Meter
1799 Festlegung des Urmeters aus Platin-Iridium.
1889 Einführung des internationalen Meterprototyps.
Urmeter
1960 Meter aus Wellenlänge
eines atomaren Übergangs von 86Kr.
Seit 1983: Lichtgeschwindigkeit festgelegt als 299.792.458 m/s.
Meter definiert als Lichtlaufstrecke in 1/299.792.458 Sekunde.
14
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Aus den SI-Einheiten abgeleitete Einheiten
Abgeleitete Einheiten mit speziellen Namen
(Derived units with special names)
Frequenz
Energie
Kraft
Druck
Leistung
El. Ladung
El. Potenzial
El. Widerstand
El. Leitfähigkeit
El. Kapazität
Magn. Fluss
Induktivität
Magn. Flusssdichte
Celsius Temperatur
…
frequency
energy
force
pressure
power
electric charge
electric potential
electric resistance
electric conductance
electric capacitance
magnetic flux
inductance
magnetic flux density
celsius temperature
hertz
joule
newton
pascal
watt
coulomb
volt
ohm
siemens
farad
weber
henry
tesla
degree celsius
Hz
J
N
Pa
W
C
V
Ω
S
F
Wb
H
T
◦C
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
SI - Vorsilben
zetta
exa
peta
kilo
tera
k M G T P E Z
giga
m
mega
n μ
milli
p
nano
f
femto
piko
atto
zepto
z a
mikro
(mindestens) diesen Bereich
sollten Sie auswendig lernen
10-2110-1810-1510-1210-9 10-6 10-3 100 103 106 109 1012 10151018 1021
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Struktur der Materie: Größenordnungen
17
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
18
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Prof. Dr. Caren Hagner
Borexino Experiment
(Gran Sasso, Italien)
Universität Hamburg
Institut für Experimentalphysik
Luruper Chaussee 149
22761 Hamburg
Email:
[email protected]
Büro:
DESY Gelände Bahrenfeld, Geb. 62, Zi. 210
Telefon:
040 8998 2297
Webseite: http://neutrino.desy.de/lehre/
Sprechstunden: nach Vereinbarung (email)
OPERA Experiment
(Neutrinooszillationen) am
Gran Sasso Untergrundlabor
(Italien)
Mein Forschungsgebiet: Neutrinophysik
(Elementarteilchenphysik, Astroteilchenphysik)
19
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kapitel 1: Kinematik
(Beschreibung der Bewegung, ohne Betrachtung von Kräften)
Vereinfachung: Wir betrachten zunächst nur Massenpunkte
Arten der Bewegung:
• geradlinige Bewegung (Translation)
• Drehbewegung (Rotation)
Geschwindigkeit = zurückgelegter Weg / dafür benötigte Zeit
Die Geschwindigkeit ist eine vektorielle Größe: Betrag (z.B. 5 m/s) und Richtung
Wir beginnen mit der geradlinigen Bewegung
20
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
a) Bewegung mit konstanter Geschwindigkeit
Weg – Zeit Diagramm
Beispiel:
Fahrt mit v = 10 m/s. (Wieviel km/h?)
Geschwindigkeit = Steigung der Geraden im Weg-Zeit Diagramm
21
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
b) Bewegung mit veränderlicher Geschwindigkeit
• v(t) ist die Steigung der Tangente an die Kurve im Weg-Zeit Diagramm.
• v(t) ist die erste Ableitung der Funktion s(t) nach der Zeit.
22
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiel für Bewegung mit veränderlicher Geschwindigkeit
23
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Überlagerung von Geschwindigkeiten
Geschwindigkeiten können vektoriell addiert werden
Beispiel: Boot im Fluss
24
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beschleunigung
25
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Bewegung mit konstanter Beschleunigung:
Beschleunigung – Zeit Diagramm
Geschwindigkeit – Zeit Diagramm
Weg – Zeit Diagramm
26
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Der freie Fall
Beobachtung:
1 Zeiteinheit
2 ZE
3 ZE
usw.
Bilder in gleichen Zeitabständen
1 Längeneinheit
4 LE
9 LE
27
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Zusammenfassung:
Konstante Geschwindigkeit
Konstante Beschleunigung
28
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Versuch zur Fallbeschleunigung
Was fällt schneller?
Papier oder Plastikteil?
1.) In Luft fällt das Plastikteil
schneller.
2.) Im Vakuum fallen beide
gleich schnell.
Alle Körper werden beim
freien Fall gleich stark
beschleunigt.
g = 9,81 m/s2
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
g ist an verschiedenen Orten auf der Erde verschieden groß
(nicht viel, aber messbar):
Trondheim (Flughafen)
g = 9.8215243 m/s2
Hamburg (Flughafen)
g = 9.8139443 m/s2
Hannover (Flughafen)
g = 9.8128745 m/s2
München (Flughafen)
g = 9.8072914 m/s2
Rom (Flughafen Ciampino)
g = 9.8034755 m/s2
Grund: Erdrotation bewirkt Fliehkräfte (am Äquator am größten)
30
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Senkrechter Wurf nach oben
31
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Überlagerung von Bewegungen: Der schiefe Wurf
32
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Versuch zum schiefen Wurf: Federkanone
Eine Feder wird gespannt und eine Kugel wird mit immer gleicher
Anfangsgeschwindigkeit abgeschossen. Der Abschusswinkel ist variabel.
α
Bei welchem Winkel ergibt sich die größte Weite?
33
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Flugbahn von Kanonenkugeln, wie man sie sich 1577 vorstellte.
(Karte von Paulus Puchner 1577, Mathematisch-Physikalische Salon Dresden)
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Berechnung der Wurfweite:
Bei welchem Winkel ist die Weite maximal? :
35
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kreisbewegung (1)
Ein Körper bewegt sich mit konstanter Bahngeschwindigkeit v auf einer Kreisbahn mit Radius r
36
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kreisbewegung (2)
37
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiel: „Bohrer“
Pressluftgetriebene Turbinen mit
Rotationsfrequenz f= 400000 min-1
Radius r = 0.5 mm
Welche Schnittgeschwindigkeit v kann erreicht werden?
38
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiel: Erddrehung
Wie groß ist die Winkelgeschwindigkeit der Erde?
Welche Bahngeschwindigkeit hat ein Mensch am Äquator ?
Welche Beschleunigung wirkt dort auf den Menschen?
Erdradius r = 6380km
39
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kapitel 2: Dynamik (Kräfte und Bewegung)
Messung von Kräften: z.B. durch Auslenkung einer Feder
Hookesches Gesetz:
Die auslenkende Kraft F ist proportional zur Auslenkung Δx
40
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Newtonschen Axiome
41
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Newtonschen Axiome: Zusammenhang zwischen Kraft und Bewegung
1. Newton‘sches Gesetz:
Ein Körper auf den keine Kräfte wirken oder die Vektorsumme der wirkenden Kräfte Null ist,
behält seine Geschwindigkeit unverändert bei.
2. Newton‘sches Gesetz: Grundgleichung der Mechanik
3. Newton‘sches Gesetz:
actio = reactio
Wenn zwei Körper Kräfte aufeinander ausüben, sind diese entgegengesetzt gleich
42
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Newtonschen Axiome (Originalversion)
Lex prima: Corpus omne perseverare in statu suo quiescendi vel movendi
uniformiter in directum, nisi quatenus a viribus impressis cogitur statum illum mutare.
Trägheitsprinzip:
Ein Körper verharrt im Zustand der Ruhe oder der gleichförmigen Bewegung,
solange die Summe aller auf ihn einwirkenden Kräfte Null ist.
Lex secunda: Mutationem motus proportionalem esse vi motrici impressae,
et fieri secundum lineam rectam qua vis illa imprimitur.
Aktionsprinzip:
Die Änderung der Bewegung einer Masse ist der Einwirkung der bewegenden
Kraft proportional und geschieht nach der Richtung derjenigen geraden Linie,
nach welcher jene Kraft wirkt.
Lex tertia: Actioni contrariam semper et aequalem esse reactionem: sive corporum
duorum actiones is se mutuo semper esse aequales et in partes contrarias dirigi.
Prinzip von “actio = reactio”: Kräfte treten immer paarweise auf.
Übt ein Körper A auf einen anderen Körper B eine Kraft aus (actio),
so wirkt eine gleichgroße, aber entgegen gerichtete Kraft von Körper B auf
Körper A (reactio).
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Gleiter (Masse M) wird mit konstanter Beschleunigung Kraft (Gewicht) bewegt.
Messung von a:
Dazu wird mit einer Lichtschranke die Zeit t gemessen, die der Gleiter für die Strecke x benötigt.
Gleiter, Masse M
Luftkissenschiene
x1
x2
x3
Gewicht
44
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
45
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Test von “actio = reactio”
46
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
„träge Masse“
Versuch: Schnelles Wegziehen der Tischdecke ->
Gläser, Teller, Besteck bleibt stehen.
Erklärung: Tischdecke hat kleine Masse, bekommt deshalb große Beschleunigung
Teller hat große Masse, wird deshalb bei gleicher Kraft nur
sehr gering beschleunigt und bleibt stehen.
47
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Überlagerung (Superposition) von Kräften:
48
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
50
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Wiederholung: Die Newtonschen Axiome
1. Newton‘sches Gesetz:
Ein Körper auf den keine Kräfte wirken oder die Vektorsumme der wirkenden Kräfte Null ist,
behält seine Geschwindigkeit unverändert bei.
2. Newton‘sches Gesetz: Grundgleichung der Mechanik
3. Newton‘sches Gesetz:
actio = reactio
Wenn zwei Körper Kräfte aufeinander ausüben, sind diese entgegengesetzt gleich
51
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Reibung
Reibung behindert Bewegung
Reibungskraft entgegen der Bewegungsrichtung
Arten von Reibung (nur einige Beispiele):
Haftreibung, Gleitreibung, Rollreibung, innere Reibung (in Fluiden),…
Reibungskraft
wächst mit der Andruckkraft
Reibungskraft
wächst mit der Geschwindigkeit
Ursache von Haft- und Gleitreibung:
Form und Struktur der beteiligten Oberflächen
elektrische Kräfte zwischen Atomen/Molekülen
der Oberflächen
52
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Haftreibung (Objekt noch in Ruhe)
Welche Kraft F ist nötig damit das Objekt anfängt sich zu bewegen?
Das Objekt wird durch die Haftreibungskraft FH festgehalten
Holz auf Stein: μH = 0.7
Stahl auf Teflon: μH = 0.04
μH heißt Haftreibungskoeffizient
Das Objekt fängt an sich zu bewegen sobald F > FH
Ab welchem Winkel rutscht der Holzklotz?
53
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Gleitreibung (Objekt bewegt sich schon)
Beim Gleiten (Rutschen) eines Objekts auf einer Oberfläche wirkt die
Gleitreibungskraft FR entgegen der Bewegungsrichtung
μGl heißt Gleitreibungskoeffizient
Holz auf Stein: μGl = 0.3
Stahl auf Teflon: μGl = 0.04
Welche Beschleunigung ergibt sich für Holzklotz auf Steinfläche (Neigungswinkel 35o)?
54
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Die Gravitationskraft:
55
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Schwerkraft und Fallbeschleunigung
RE
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Arbeit und Energie
SI-Einheit der Arbeit (Energie): 1 Joule 1 J = 1 Nm
Weitere gebräuchliche Einheiten:
1 cal = 4.184 J
1 kWh = 3600000 J = 3.6∙106J
Bei konstanter Kraft F gilt:
Hubarbeit: Arbeit, die nötig ist um eine Masse m um Höhe Δh anzuheben
Potentielle Energie (beim Heben):
Die Masse m hat durch das Anheben die potentielle Energie Epot gewonnen
57
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiel: Flaschenzug
Mit welcher Kraft F muss man ziehen um
das Gewicht anzuheben?
Man benötigt zum Heben 4x weniger Kraft, muss aber eine 4x längere Strecke bewältigen
58
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Arbeit und Energie beim Dehnen einer Feder
59
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Wiederholung: Arbeit und Energie
Arbeit = Kraft ∙ Weg
Einheit: 1 Joule
Für konstante Kraft (Richtung entlang des Weges s) gilt:
Allgemein gilt (falls F sich je nach Position s ändert):
W = ∫ F(s) ds
W=F∙s
dW = F(s) ∙ ds
Hubarbeit zum Heben einer Masse um Höhendifferenz Δh:
Whub = m g Δh
Arbeit zum Dehnen einer Feder (Federkonstante D) um Strecke x:
Wdehn = ½ D x2
Potentielle Energie:
Gravitation Epot = mgh,
Feder Epot = ½ D x2
Kinetische Energie: Ekin = ½ m v2
Gesamtenergie: Eges = Epot + Ekin
Energieerhaltung: Die Gesamtenergie ist konstant
60
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kinetische Energie
(Energie die in der Bewegung steckt)
Energieerhaltung: Die Summe von potentieller und kinetischer Energie ist konstant
61
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Das Hebelgesetz (1)
62
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Das Hebelgesetz (2): Kraftrichtung nicht senkrecht
Nur die zum Hebelarm senkrechte Kraftkomponente spielt im Hebelgesetz eine Rolle
63
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Drehmoment
64
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Anwendung: Drehmomentschlüssel
Werkzeug um Schrauben mit genau definiertem Drehmoment festzuziehen.
Bei diesem Modell gilt z.B.
Max. Drehmoment einstellbar im Bereich
10 – 60 Nm
65
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Gleichgewicht
Ein System ist im Gleichgewicht, wenn:
• Die Summe aller Kräfte gleich Null ist und
• Die Summe aller Drehmomente gleich Null ist.
Arten des Gleichgewichts:
Auslenkung
erfordert Energiezufuhr
Auslenkung
liefert Energie
Auslenkung
erfordert keine Energie
und liefert keine Energie
66
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Impuls (engl. momentum)
67
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Versuch: Wasserrakete
68
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Versuch zum Impuls: 2 Wagen auf Luftkissenschiene
69
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Impulserhaltung
Kommt in allen Bereichen vor:
• Stöße zwischen Himmelskörpern
(z.B. Planeten mit Meteoriten)
• Billard, Fussball,…
• Stöße zwischen Atomen und
Molekülen,
• Comptoneffekt (Stoß zwischen Photon
und Elektron)
• Elementarteilchenphysik
Computer animation of a Newtons' cradle
Source: Wikipedia, Author: Dominique Toussaint.
This file was a finalist in Picture of the Year 2006 and was selected as picture of the day
on Wikimedia Commons for 29 May 2007 .
70
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Anwendung in der Teilchenphysik
Im LHC am CERN werden Protonen auf Protonen geschossen.
Jedes fliegt fast mit Lichtgeschwindigkeit . Der Gesamtimpuls ist Null.
Man beobachtet und misst die Impulse der beim Stoß entstehenden neuen Teilchen.
71
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Kräfte bei Drehbewegungen:
Zentrifugalkraft und Zentripetalkraft
72
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiele:
73
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Klausur
Morgen: 23.11.2013 von 9:45 – 11Uhr
Ort: Audimax (Uni Hauptgelände Dammtor)
Einlass ab 9:30 Uhr
Hilfsmittel: Nur Taschenrechner (keine Formeln, Texte usw. einprogrammieren)
Nachschreibklausur: Sa 14.12.2013 von 9.45 - 11.00 Uhr
Achtung: Ort für Nachschreibklausur ist Jungiusstr. 9
74
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Beispiel: Umlaufbahn von geostationären Satelliten
http://lms.seos-project.eu/learning_modules/remotesensing/remotesensing-c02-p01.html
75
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
So überfüllt sind inzwischen die Satellitenumlaufbahnen!
76
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Trägheitsmoment und Drehimpuls
77
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Drehimpulserhaltung:
Beispiel Pirouette, Drehstuhlversuch
Beobachtung: Durch Anziehen der Arme (kleinerer Radius) vergrößert sich die
Rotationsgeschwindigkeit!
78
Physik für Biologie und Zahnmedizin WS2013/14
Prof. Dr. Caren Hagner
Gerade Bewegung - Drehbewegung
79