Mathematik 2 - Moodle ZHAW

Mathematik 2
Statistik
Institut für Angewandte Simulation
Autor:
Olivier Merlo
Datum:
16.2.2017
Version:
1.1
Studiengang:
Chemie
Zürcher Fachhochschule
Das Skript: Dieses Skript wurde von Olivier Merlo geschrieben und wurde im Laufe der Jahre immer wieder überarbeitet. © 2016, Olivier Merlo, ZHAW. Dieses Skript darf ganz oder in Teilen weitergegeben und nicht kommerziell verwendet werden, wobei dieser Copyright‐Vermerk mitkopiert werden muss. Kommerzielle Verwendung nur mit Bewilligung des Autors. Sowohl Olivier Merlo als auch die ZHAW lehnen jegliche Haftung ab für Schäden, die sich aus der Verwendung dieses Skriptes ergeben. Inhaltsverzeichnis
1 Vorwort
1.1 Prüfungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Literatur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.3 Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
5
6
6
2 Einführung
2.1 Begriff Statistik . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Der Begriff der Wahrscheinlichkeit . . . . . . . . . . . . . . . . .
2.3 Wichtige Gesetze . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Kombinatorik . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4.1 Ziehung von Kugeln mit Berücksichtigung der Reihenfolge
2.4.2 Ziehung von Kugeln ohne Berücksichtigung der Reihenfolge
2.5 Bedingte Wahrscheinlichkeit . . . . . . . . . . . . . . . . . . . . .
2.6 Ereignisbaum . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.7 Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . .
7
7
7
8
11
12
12
14
15
16
3 Deskriptive (beschreibende) Statistik
3.1 Datenerfassung . . . . . . . . . . . . .
3.2 Datenbearbeitung . . . . . . . . . . . .
3.3 Klassierung . . . . . . . . . . . . . . .
3.4 Lagemass für ordinalskalierte Daten .
3.4.1 Median . . . . . . . . . . . . .
3.4.2 Quantile . . . . . . . . . . . . .
3.5 Lagemass für metrisch skalierte Daten
3.6 Standardisieren . . . . . . . . . . . . .
3.7 Zusammenfassung . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
17
18
19
20
20
21
21
23
23
4 Verteilungen
4.1 Diskrete Verteilungen . . . . . . . . . . . . . . . . . . . .
4.1.1 Uniforme Verteilung . . . . . . . . . . . . . . . . .
4.1.2 Binomialverteilung B(n,p) . . . . . . . . . . . . . .
4.1.3 Poissonverteilung . . . . . . . . . . . . . . . . . . .
4.2 Kontinuierliche Verteilungen . . . . . . . . . . . . . . . . .
4.2.1 Uniforme Verteilung . . . . . . . . . . . . . . . . .
4.2.2 Maxwell-Boltzmann Verteilung . . . . . . . . . . .
4.2.3 Exponentialverteilung . . . . . . . . . . . . . . . .
4.2.4 Normalverteilung . . . . . . . . . . . . . . . . . . .
4.3 Zusammenhang zwischen den verschiedenen Verteilungen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
25
25
26
26
28
29
31
32
33
34
36
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
INHALTSVERZEICHNIS
4.4
Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . .
38
5 Statistische Tests
5.1 Freiheitsgrade . . . . . . . . . . . . . . . .
5.2 Schätzer . . . . . . . . . . . . . . . . . . .
5.2.1 Beispiele für verschiedene Schätzer
5.3 Vertrauensintervall . . . . . . . . . . . . .
5.4 Hypothesen-Tests . . . . . . . . . . . . . .
5.4.1 Hypothese . . . . . . . . . . . . . .
5.5 Welcher Test? . . . . . . . . . . . . . . . .
5.5.1 Vorgehensweise . . . . . . . . . . .
5.6 Test auf Normalverteilung . . . . . . . . .
5.6.1 QQ-Plot . . . . . . . . . . . . . . .
5.6.2 Kolmogorov-Smirnov Test . . . . .
5.6.3 χ2 -Test auf Normalverteilung . . .
5.6.4 t-Test . . . . . . . . . . . . . . . .
5.6.5 Grubbs Test . . . . . . . . . . . . .
5.7 Zusammenfassung . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
39
39
40
40
41
43
43
45
47
47
47
50
51
54
58
59
6 Messfehler
6.1 Ein Messwert . . . . . . . . . . . . . . .
6.2 Fehlerfortpflanzung . . . . . . . . . . . .
6.3 Korrelation . . . . . . . . . . . . . . . .
6.3.1 Deskriptive Statistik . . . . . . .
6.4 Regression . . . . . . . . . . . . . . . . .
6.4.1 Methode der kleinsten Quadrate
6.5 Zusammenfassung . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
61
61
62
63
63
64
65
72
7 Boltzmann Verteilung
7.1 Diskrete Boltzmann Verteilung . . . .
7.1.1 spezifische Molwärme . . . . .
7.2 kontinuierliche Boltzmann Verteilung .
7.2.1 Maxwell-Boltzmann Verteilung
7.3 Zusammenfassung . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
73
73
73
74
74
75
8 Tabellen
8.1 Normalverteilung . . . . . . .
8.2 Student t Tabelle . . . . . . .
8.3 χ2 − T abelle . . . . . . . . .
8.4 Kolmogorov Smirnov Test . .
8.5 Grubbs-Test (Ausreissertest)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
77
77
78
79
80
81
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Kapitel 1
Vorwort
Es handelt sich hier um eine sehr knappe Einführung in die wichtigsten Begriffe
und Methoden der Statistik. Spezielles Gewicht wird auf den Begriff der Verteilung gelegt, insbesondere im Zusammenhang mit der statistischen Physik.
Wer sich später wirklich mit Statistik beschäftigen muss, z.B. im Zusammenhang mit Qualitätskontrolle, kommt um Weiterbildung und den Gebrauch einer
anständigen Statistiksoftware (nicht Excel) nicht herum.
1.1
Prüfungen
Die Anerkennung des Kurses wird durch ein Modulexamen am Ende des Semesters und diverse Examen während dem Semester geprüft. Die Modulprüfung
zählt zu 70% und die Prüfungen während des Semesters zu 30% zur Gesamtbeurteilung.
Die Note N errechnet sich immer aus der erreichten Punktzahl PE und den
Maximalpunktzahl PM mittels:
E
N = 1 + 5 PPM
Die Prüfung während des Semesters erfolgt am
1. Freitag, 21. April 2017
Bei einer Absenz an einer Prüfung muss eine schriftliche Begründung bis
spätestens 2 Wochen nach der Prüfung bei mir eintreffen. Falls dies nicht erfolgt,
muss die Prüfung leider mit einer Note 1 gewertet werden.
Die Vornote des Kurses ist der Mittelwert der 3 Prüfungen während des
Semesters.
5
6
KAPITEL 1. VORWORT
1.2
Literatur
Das vorliegende Skript basiert auf dem Skript auf den Büchern:
1. Köhler und Schachtel, Biostatistik, Springer Verlag.
2. Moore, McCabe, Duckworth and Sclove, The practice of business statistics, Freeman and Company.
3. Für Regression: Mager, Moderne Regressionsanalyse, Otto Sale Verlag.
1.3
Definitionen
R
N
∈
{a, b, c, . . . , d}
[a, b]
(a, b)
|A |
A1 ∩ A2
A1 ∪ A2
Ac
Ø
lim
l
P
Menge der reellen Zahlen
Menge der natürlichen Zahlen
ist Element von
Menge der dargestellten Elemente
abgeschlossenes Intervall von a nach b
offenes Intervall von a nach b
Anzahl der Elemente der Menge A
Schnittmenge von A1 mit A2
Vereinigung der Mengen A1 mit A2
Komplement der Menge A
leere Menge
Grenzwert
Summe der Elemente von Index i bis l
k=i
A⇒B
A⇔B
=
≈
∼
Aus A folgt B
Aus A folgt B und umgekehrt
gleich
näherungsweise
proportional
Kapitel 2
Einführung
2.1
Begriff Statistik
7. Jh.: Statistik = Lehre von den Staatsmerkwürdigkeiten (Anzahl der Einwohner, der Soldaten; Steueraufkommen, etc.) [lat. statisticum: den Staat betreffend]
• als Datensammlung (z.B. Meldestatistik, Unfallstatistik)
• als mathematische Funktion (Schätzstatistik, Teststatistik)
• als Wissenschaft (Statistische Methodenlehre, Statistische Physik)
Statistische Methoden sind in allen empirischen Wissenschaften zur Beschreibung und Beurteilung der erhobenen oder gemessenen Daten notwendig.
In diesem einführenden Kapitel werden die wichtigsten Begriffe und Gesetze
vorgestellt. Wir arbeiten dabei mit dem Beispiel des Würfelns oder auch mit
dem Werfen einer Münze.
2.2
Der Begriff der Wahrscheinlichkeit
Beispiel: Ein Würfel wird sehr oft geworfen. Das Werfen eines Würfels ist
ein Zufallsexperiment. Die relative Häufigkeit die Zahlen 1, 2, . . . bzw. 6
zu würfeln konvergiert gegen einen bestimmten Wert p(Wurf=1), p(Wurf=2)
. . . p(Wurf=6). Der Wert p(. . . ) wird empirische Wahrscheinlichkeit genannt. Dabei bedeutet p(. . . ) = 0 ein unmögliches Ereignis (z.B. Werfen der
Zahl 7) und p(. . . ) = 1 bedeutet ein sicheres Ereignis (man wirft eine der Zahlen 1 bis 6). Das Elementarereignis ω ist das Ereignis eines Experimentes,
z.B. ”Werfen der Zahl 5”. Der Ereignisraum Ω ist die Menge aller möglicher
Elementarereignisse ωi ; hier:
Ω = {1, 2, 3, 4, 5, 6} .
7
8
KAPITEL 2. EINFÜHRUNG
Definition 2.1 (Elementare Definitionen)
Die Menge aller Elementarereignisse eines Zufallsexperiments wird Ereignisraum Ω genannt. Ein einzelnes Element ωi des Ereignisraums wird Elementarereignis genannt. Die empirische Wahrscheinlichkeit das Elementarereignis
zu erhalten wird durch p(ωi ) gegeben. Das Ereignis wird nicht erhalten, falls
p(ωi ) = 0 ist. Falls p(ωi ) = 1 ist, so ist dies ein sicheres Ereignis. Eine Teilmenge A von Ω wird Ereignis genannt.
2.3
Wichtige Gesetze
In den nächsten Kapiteln gehen wir nicht von Experimenten aus, sondern es
wird um theoretische Überlegungen gehen.
Beispiel: Wir betrachten das Werfen von einem Würfel. Die Elementarereignisse ωi sind gegeben durch das Werfen der Anzahl Augen 1, 2, 3, . . . , 6. Die
Anzahl der Elementarereignisse ist also gegeben durch |Ω| = 6. Die Anzahl
Möglichkeiten die Anzahl Augen gleich 1 zu werfen ist 1,A(ω = 1) = 1, da
genau eine Möglichkeit w1 besteht, diese Zahl zu würfeln. Damit erhält man
die Wahrscheinlichkeit eine Anzahl Augen von 1 zu werfen von p(A) = 61 . Man
hat dazu die Anzahl der Möglichkeiten durch die gesamte Anzahl der
Ereignisse dividiert. Man geht also davon aus, dass alle Elementarereignisse
die gleiche Wahrscheinlichkeit besitzen einzutreffen.
Definition 2.2 (Laplace Annahme)
Hat der Ereignisraum Ω endlich viele Elemente ωi mit der gleichen Wahrscheinlichkeit p. Dann gilt für die Berechnung der Wahrscheinlichkeit:
p(A) =
|A|
|Ω|
Anzahl Elementarereignisse in A
= Anzahl Elementarereignisse in Ω
Beispiel: Wie gross ist die Wahrscheinlichkeit mit einem Würfel eine gerade
Anzahl Augen zu werfen?
Man hat die Elementarereignisse Werfen von 2, 4 oder 6. Wenn man aber die
Anzahl Augen gleich 2 geworfen hat, kann man nicht die 4 geworfen haben. Diese
Ereignisse schliessen einander aus. Solche Ereignisse werden disjunkte Ereignisse genannt. Bei disjunkten Ereignissen ist die gesamte Anzahl der Ereignisse
gleich der Summe der einzelnen Ereignisse. In diesem Fall ist A = {2, 4, 6}. Verallgemeinert gesagt hat man die Ereignisse A1 = {2}, A2 = {4} und A3 = {6},
und das Ereignis eine gerade Anzahl Augen zu würfeln ist gegeben durch die
Vereinigung der Mengen Ai . Somit besitzt die Menge A = ∪3i=1 Ai = {2, 4, 6}
insgesamt 3 Elementarereignisse und die Wahrscheinlichkeit eine gerade Anzahl
3
1
Augen zu würfeln ist gegeben durch p(A) = |A|
|Ω| = 6 = 2 .
Definition 2.3 (Disjunkte Ereignisse)
Die Ereignisse A1 und A2 werden disjunkt genannt, falls die Schnittmenge A1 ∩
A2 = Ø die leere Menge ist; also wenn sie keine gemeinsamen Elemente besitzen.
Die Anzahl der Elemente der Menge A = A1 ∪A2 ist dann die Summe der Anzahl
Elemente der beiden Teilmengen.
|A| = |A1 | + |A2 |, falls A1 ∩ A2 = Ø.
2.3. WICHTIGE GESETZE
9
Anmerkung:
1. Hat man n Ereignisse, die alle disjunkt sind, so ist die Wahrscheinlichkeit
Ereignis A1 oder A2 oder . . . oder An zu erhalten (A = ∪ni=1 Ai ) gegeben
durch
|A1 |+|A2 |+...+|An |
p(A) = |A|
= p(A1 ) + p(A2 ) + . . . + p(An ).
|Ω| =
|Ω|
Beispiele 2.1 Gesucht ist die Wahrscheinlichkeit, beim Werfen mit zwei
Würfeln eine Gesamtaugenzahl von 7 zu erhalten.
Es existieren die Möglichkeiten {1 | 6, 2 | 5, 3 | 4, 4 | 3, 5 | 2, 6 | 1}. Dabei bedeutet 1 | 6, dass wir mit dem ersten Würfel die Zahl 1 und mit dem zweiten
Würfel die Zahl 6 werfen. Alle diese Ereignisse sind disjunkt zueinander. Das
Ereignis {1 | 6} ist verschieden von dem Ereignis {6 | 1}. Es spielt also eine
Rolle, mit welchem Würfel man welche Zahl wirft. Damit ist die Anzahl der
‘günstigen Ereignisse‘ durch |A| = 6 gegeben. Der Ereignisraum besitzt 36 Ereignisse |Ω| = 36. Daher ist die Wahrscheinlichkeit, dass die Augenzahl gleich
6
= 16 .
7 ist: p(A) = 36
Zusatz: Wie gross ist die Wahrscheinlichkeit, dass die Augenzahl gleich 6 ist?
5
)
(Lösung: p(ω = 6) = 36
Beispiel: Man betrachtet wieder das Werfen mit 2 Würfeln. Wieviele Anzahl Kombinationen (Ereignisse) existieren insgesamt?
Es existieren 6 Möglichkeiten für den ersten Würfel und 6 weitere für den
zweiten Würfel, nämlich je die Zahlen 1 bis 6. Es hat keinen Einfluss auf den
2. Würfel, was ich mit dem ersten Würfel geworfen habe. Solche Ereignisse
werden unabhängige Ereignisse genannt. Hier ist die gesamte Anzahl der
Ereignisse gegeben durch Multiplikation der Anzahl der einzelnen Ereignissen
|Ω| = 6 · 6 = 36.
Man erhält also zuerst ein Ereignis und anschliessend ein zweites Ereignis.
Definition 2.4 (Unabhängige Ereignisse)
Man habe die unabhängigen Ereignisse A1 und A2 . Dann ist die Menge A =
{ωA1 | ωA2 } mit ωA1 ∈ A1 und ωA2 ∈ A2 . Die Anzahl der Elemente der Menge
A ist dann das Produkt der Anzahl Elemente der beiden Teilmengen.
|A| = |A1 | · |A2 |, falls A1 unabhängig von A2 ist.
10
KAPITEL 2. EINFÜHRUNG
Anmerkung
1. Hat man 2 Ereignisse die voneinander unabhängig sind, so kann die Wahrscheinlichkeit, Ereignis A1 und A2 zu erhalten, berechnet werden. Man
benutzt dabei die einzelnen Wahrscheinlichkeiten in den Teilmengen. Man
|A2 |
1|
definiert p(A1 ) = |A
|Ω1 | und p(A2 ) = |Ω2 | , wobei die Ωi die gesamte Anzahl
der Ereignisse von den Ereignissen i ist. Da die Ereignisse unabhängig sind,
ist die Gesamtanzahl der Ereignisse gegeben durch |Ω| = |Ω1 | · |Ω2 |. Somit
|A1 |·|A2 |
ist die Wahrscheinlichkeit von A gegeben durch p(A) = |A|
|Ω| = |Ω1 |·|Ω2 | =
p(A1 ) · p(A2 ).
Man findet in Büchern häufig, dass die unabhängigen Ereignisse mit diesem Resultat definiert werden.
2. Es ist für Studierende nicht immer einfach zu entscheiden, ob zwei Ereignisse disjunkt oder unabhängig sind. Häufig funktioniert eine Verbalisierung mit dem Worten und resp. oder.
Ist man daran interessiert, ob der Würfel 2 oder 4 oder 6 anzeigt, so sind
die Ereignisse 2 resp. 4 resp. 6 zu würfeln disjunkt.
Ist man daran interessiert, ob zuerst mit dem ersten Würfel etwas geworfen wird und anschliessend mit einem anderen Würfel geworfen wird so
ist das Werfen der beiden Würfel unabhängig.
Ist man daran interessiert, dass der erste Würfel eine gerade Anzahl Augen
anzeigt und der zweite die Anzahl Augen 2 oder 5. So hat man disjunkte
und unabhängige Ereignisse.
2.4. KOMBINATORIK
11
Beispiele 2.2
1. Man betrachtet wieder das Würfeln mit 2 Würfeln. Wie gross ist die
Wahrscheinlichkeit, dass man mit dem ersten Würfel eine gerade Zahl
würfelt und mit dem 2. Würfel die Zahl 3 oder 5?
Es existieren 3 Möglichkeiten mit dem ersten Würfel eine gerade Zahl und
2 Möglichkeiten mit dem 2. Würfel die Zahlen 2 oder 5 zu würfeln.
Die Ereignisse sind disjunkt, daher ist die gesamte Anzahl der Ereignisse
gegeben durch |A| = 3 · 2 = 6. Die Wahrscheinlichkeit dieses Ereignis zu
erhalten ist also gegeben durch p(A) = 61 .
2. Wie gross ist die Wahrscheinlichkeit mit einem Würfel eine gerade Zahl
und mit dem anderen Würfel die Zahlen 2 oder 5 zu würfeln?
Man hat also 6 Möglichkeiten mit dem ersten Würfel eine gerade Zahl
und mit dem 2. Würfel die Zahl 2 oder 5 zu würfeln. Man hat natürlich
umgekehrt mit dem 2. Würfel eine gerade Zahl zu würfeln usw. auch 6
Möglichkeiten. Die Wahrscheinlichkeit, dieses Ereignis A zu erhalten ist
11
aber gegeben durch p(A) = 36
. Das Problem liegt darin, dass die beiden Mengen nicht disjunkt sind. Die Schnittmenge besitzt ein Element
|A1 ∩ A2 | = 1. Welches ist dieses?
2.4
Kombinatorik
In der Kombinatorik berechnet man die oben betrachtete Anzahl der günstigen
Ereignisse |A| und die Anzahl aller Ereignisse |Ω|.
Wir benutzen eigentlich nur die Regeln für disjunkte und unabhängige Ereignisse um die Anzahl eines bestimmten Ereignisses zu berechnen.
Bemerkung 2.1 (Komplementäre Ereignisse) Manchmal ist es einfacher
das komplementäre Ereignis Ac zu betrachten. Dann gilt |A| = |Ω| − |Ac |.
Triviales Beispiel
Wir wollen wissen, wieviele Möglichkeiten man besitzt mit 1 Würfel keine der
Zahlen 1, 2, 3, 4, 5 zu würfeln. Das komplementäre Ereignis ist, die Zahl 6 zu
würfeln. Somit ist die Anzahl Möglichkeiten gegeben durch 6 − 1 = 5.
Historisch gesehen betrachtet man in der Kombinatorik eine Urne mit verschiedenfarbigen Kugeln, aus welcher man Kugeln zieht. Dies kann mit oder ohne
Zurücklegen der gezogen Kugel passieren. Auch die Reihenfolge des Ziehens
kann eine Rolle spielen.
12
KAPITEL 2. EINFÜHRUNG
2.4.1
Ziehung von Kugeln mit Berücksichtigung der Reihenfolge
1. mit Zurücklegen
In diesem Fall ist jedes Ziehen einer Kugel unabhängig von den anderen
Ereignissen(bei k-maligem Ziehen). Jedes Mal hat man bei einer Urne mit
n Kugeln, n Möglichkeiten und erhält so die Gesamtzahl der Möglichkeiten zu |Ω| = nk .
Beispiel
(a) Mehrmaliges Werfen eines Würfels oder einer Münze.
(b) Wie gross ist die Wahrscheinlichkeit bei 3 maligem Werfen eines
Würfels dreimal eine gerade Anzahl Augen zu erhalten?
Lösung:
|A| = 33 und |Ω| = 63 ⇒ p(A) =
33
63
=
1
8
2. ohne Zurücklegen
In diesem Fall hat man bei einer Urne mit n Kugeln das erste Mal n
Möglichkeiten, anschliessend n−1 Möglichkeiten bis n−k+1 Möglichkeiten
beim k-ten Mal zu ziehen. So ergibt sich die Gesamtzahl der Möglichkeiten
n!
zu |Ω| = n · (n − 1) · (n − 2) . . . (n − k + 1) = (n−k)!
. Dabei ist die Funktion
n! durch n! = n · (n − 1) · (n − 2) . . . 1 definiert.
Beispiel
(a) Die Anzahl der höchstens vierstelligen Zahlen mit lauter verschiedenen Ziffern von 0-9 ist. |A| = 10 · 9 · 8 · 7 = 5040. Man beachte, dass
hier die Ziffer 0 auch am Anfang stehen kann.
2.4.2
Ziehung von Kugeln ohne Berücksichtigung der Reihenfolge
Falls die Reihenfolge keine Rolle spielt, so muss man sich überlegen auf wieviele
Arten man k-Objekte auf die k-Plätze verteilen kann. Dies ist gegeben durch
k · (k − 1) · (k − 2) . . . 1 = k!. Man kann sich das wie hinlegen ohne zurücknehmen
vorstellen. Die verschiedenen Anordnung werden Permutationen genannt.
Da alle diese Ereignisse unabhängig voneinander sind, ergibt sich dann die Anzahl der Ereignisse durch Division durch diese k! Möglichkeiten.
2.4. KOMBINATORIK
13
Beispiele
1. mit Zurücklegen
Betrachten wir den Fall den 3-maligen Wurf einer Münze. Wir haben dann
die Ereignisse 0, 1, 2 resp. 3 Mal Kopf zu werfen. Diese Ereignisse besitzen aber nicht die gleiche Wahrscheinlichkeit, daher ist bei dieser betrachtungsweise die Laplace Annahme nicht gültig. Diese Wahrscheinlichkeiten
können berechnet werden, indem man die Anzahl Permutationen der einzelnen Ereignisse bestimmt.
Dazu schreibt man am besten eine 0 für das Werfen von Kopf und eine
1 für das Werfen von Zahl. Dann schreibt sich das Ereignis 0 mal Werfen
von Kopf als 111. Schreiben wir eine Tabelle aller möglichen Ereignisse
mit den Anzahl der Permutationen.
Ereignis Anzahl Permutationen
000
1
001
011
111
1
Die Anzahl der Ereignisse können natürlich auf verschiedene Arten berechnet werden. Ich werde meine betrachtungsweise am Beispiel 001 zeigen.
Wir verteilen am Anfang 3 verschiedene Elemente auf 3 Plätze. Wir betrachten hier die beiden 0 als verschieden. Damit erhält man 3! = 6
Möglichkeiten, da es ohne zurücklegen ist. Nun betrachten wir die Elemente die gleich sind. Die beiden 0 werden nun wieder als gleich betrachtet.
Man kann diese vertauschen und erhält das gleiche Bild, damit erhält dass
man am Anfang alle Ereignisse doppelt gezählt hat. Damit erhält man die
3!
Anzahl Ereignisse mit 2 Mal 0 und einmal 1 zu 2!·1!
= 3.
2. ohne Zurücklegen
(a) Die Anzahl der verschiedenen Kombinationen von Lottozahlen (man
49!
.
zieht 6 Kugeln aus 49 verschiedenen Kugeln) ist gegeben durch (49−6)!
Nun spielt es aber keine Rolle, in welcher Reihenfolge die Zahlen gezogen werden. Diese 6 Zahlen können auf 6! verschiedene Arten ge49!
Möglichkeiten. Diese
schrieben werden. Daher ergeben sich (49−6)!6!
Kombination
ist
so
häufig,
dass
sie
eine
eigene
Notation bekommen
49
49!
hat
= (49−6)!6! . (Gesprochen 49 tief 6).
6
Es gilt:
49
49
=
6
49 − 6
(b) Man hat in einem Modul 7 Vorlesungen, wobei man 4 davon besuchen
muss. Wieviele verschiedene Modulzusammenstellungen existieren?
|A| =
7
4
=
7·6·5·4
4!
= 35
14
KAPITEL 2. EINFÜHRUNG
Satz 2.1 (Berechnung der Anzahl Permutationen)
Um die Anzahl Permutationen zu berechnen betrachtet man am besten alle
Möglichkeiten und dividiert durch die Anzahl der identischen Möglichkeiten. Wir
betrachten k verschiedenfarbige Kugeln. Von jeder Kugelfarbe i besitzen wir ni
k
P
ni und die Gesamtzahl der AnordnunKugeln. Die Gesamtzahl ist also n =
i=1
gen ist dann gegeben durch n! (mit Unterscheidung). Jede Kugelart besitzt ni !
Permutationen. Somit erhält man die Anzahl der Möglichkeiten zu n1 !·nn!
.
2 !...nk !
2.5
Bedingte Wahrscheinlichkeit
Beispiel
1. Neulich erfuhren wir durch die Wettervorhersage, dass es am Samstag
mit fünfzig-prozentiger Wahrscheinlichkeit und am Sonntag ebenfalls mit
fünfzig-prozentiger Wahrscheinlichkeit regnen werde. Wie gross ist nun die
Wahrscheinlichkeit, dass es am Wochenende regnet?
Anmerkung: Das Wetter von Morgen hat einen starken kausalen Zusammenhang mit dem Wetter von heute. Daher ist das Ereignis äm Sonntag
regnet es”nicht unabhängig vom Ereignis äm Samstag regnet es”. Wenn
die Ereignisse vollkommen unabhängig wären, so wäre die Wahrscheinlich2
keit gegeben durch p(A) = 1 − 21 .
2. Wir betrachten die folgenden Wahrscheinlichkeiten.
(a) ein Schweizer hat die Muttersprache deutsch
(b) eine Person, die die Muttersprache deutsch hat, ist Schweizer
Antwort
Ohne die Auslandsschweizer ist die Wahrscheinlichkeit (a) ca. 60%. Für
(b) gilt: weltweit haben ca. 100 Millionen Menschen die Muttersprache
deutsch. Daraus ergibt sich, dass die Wahrscheinlichkeit (b) gegeben ist
6
·0.6
durch 7·10
100·106 = 0.042 = 4.2%
Definition 2.5 (Bedingte Wahrscheinlichkeit)
Unter bedingter Wahrscheinlichkeit versteht man die Wahrscheinlichkeit, dass
ein Ereignis eintritt, vorausgesetzt dass ein anderes Ereignis vorher schon
eingetreten ist. Die Wahrscheinlichkeit, dass ein Ereignis A eintritt, falls das
Ereignis B schon eingetroffen ist, ist gegeben durch:
p(A | B) = Anzahl von A in B =
Anzahl von B
|A∩B|
|B|
=
|A∩B| |Ω|
|Ω| |B|
=
p(A∩B)
p(B)
Kommentar
Sind 2 Ereignisse A und B unabhängig voneinander so gilt p(A ∩ B) =
p(A) · p(B). Dies führt auf p(A | B) = p(A∩B)
= p(A)·p(B)
= p(A). Das heisst
p(B)
p(B)
2.6. EREIGNISBAUM
15
das Eintreffen vom Ereignis B hat keinen Einfluss auf das Eintreten von Ereignis
A (anders gesagt: die Wahrscheinlichkeit, dass A eintrifft ist gleich gross, ob B
vorher eingetroffen ist oder nicht).
2.6
Ereignisbaum
Beispiel
Wir betrachten den Münzwurf einer nicht genau symmetrischen Münze. Diese
habe die Wahrscheinlichkeit p = 0.4 Kopf (K) anzuzeigen und die Wahrscheinlichkeit q = 1 − p = 0.6 Zahl (Z) anzuzeigen. Nach zweimaligen Werfen der
Münze wollen wir wissen, wie gross die Wahrscheinlichkeit ist, dass wir 1 Mal
Kopf und 1 Mal Zahl geworfen haben.
In der Abbildung 2.1 haben wir den Ereignisbaum dieses Experiments abgebildet. Wir fangen ganz oben an und können beim ersten Mal entweder Kopf
oder Zahl werfen. Man zeichnet für jedes mögliche Ereignis eine Verzweigung
und schreibt darüber, wie gross die Wahrscheinlichkeit für dieses Ereignis ist.
Die Ereignisse (K) und (Z) sind disjunkt und zusätzlich sind es alle Möglichkeiten, die die Münze besitzt. Somit muss die Summe der Wahrscheinlichkeiten
von (K) und (Z) 1 ergeben. Anschliessend können bei jedem Zweig wieder die
beiden Ereignisse Kopf oder Zahl eintreten. Der zweite Wurf ist unabhängig
vom ersten. Falls man sich auf einem Zweig herunter bewegt sind die Ereignisse daher unabhängig voneinander. Man erhält die Wahrscheinlichkeit, für
den betrachteten Zweig durch Multiplikation der entsprechenden Wahrscheinlichkeiten. In der folgenden Tabelle sind die Wahrscheinlichkeiten des gezeigten
Ereignisbaums gegeben.
Ereignis Wahrscheinlichkeit
KK
p = 0.4 · 0.4 = 0.16
KZ
p = 0.4 · 0.6 = 0.24
ZK
p = 0.6 · 0.4 = 0.24
ZZ
p = 0.6 · 0.6 = 0.36
Falls man nur an den Ereignissen 2 Mal Kopf, 2 Mal Zahl und 1 Mal Kopf
und 1 Mal Zahl interessiert ist, dann sind die Ereignisse KZ und ZK die gleichen
und da diese Ereignisse disjunkt sind, können die beiden Wahrscheinlichkeiten
einfach addiert werden. So erhält man die Wahrscheinlichkeit P = 0.48, dass
man 1 Mall Kopf und 1 Mal Zahl wirft.
Die folgenden Regeln gelten in einem Ereignisbaum:
• Die Summe der Wahrscheinlichkeiten nach einer Verzweigung ist 1 (disjunkte Ereignisse, von denen eines eintreten muss; jeder Zweig bedeutet
eine Möglichkeit für den Fortgang).
• Längs eines Weges müssen die Wahrscheinlichkeiten multipliziert werden
(unabhängige Ereignisse).
• Wenn verschiedene Wege zum gleichen Resultat führen, müssen deren
Wahrscheinlichkeiten addiert werden (disjunkte Ereignisse).
16
KAPITEL 2. EINFÜHRUNG
K
0.4
p=
Z
q=
0.4
gig
en
ha
p=
0.4
un
ab
0.6
p=
0.4
q=
Z
.4
q=0
K
K
Z
disjunkt
Abbildung 2.1: Der Ereignisbaum des 2maligen Werfens einer Münze, mit den
Wahrscheinlichkeiten p = 0.4 für Kopf (K) und p = 0.6 für Zahl (Z).
2.7
Zusammenfassung
Nach der Laplace Annahme ist die Wahrscheinlichkeit, dass ein Ereignis eintritt, gegeben durch die Anzahl der Ereignisse dividiert durch die Anzahl aller
Ereignisse. Man geht dabei davon aus, dass alle Ereignisse gleich wahrscheinlich
sind.
Man unterscheidet zwischen unabhängigen und disjunkten Ereignissen. Bei unabhängigen Ereignissen werden die Anzahl der Möglichkeiten multipliziert und
bei den disjunkten addiert.
Dies führt darauf, dass die Wahrscheinlichkeiten auch multipliziert oder addiert
werden können. (Hier muss man aufpassen: Wahrscheinlichkeit bezüglich was?)
Folgenden Regeln sind zur Berechnung der Anzahl Möglichkeiten wichtig:
Berechnung
Ziehen von Kugeln mit zurücklegen
Reihenfolge spielt Rolle
Ziehen von Kugeln ohne zurücklegen
Reihenfolge spielt Rolle
Ziehen von Kugeln ohne zurücklegen
Reihenfolge spielt keine Rolle
Noch zwei Kontrollfragen.
1. Was ist eine bedingte Wahrscheinlichkeit?
2. Was ist ein Ereignisbaum und wie berechnet sich die Wahrscheinlichkeit
für ein Ereignis?
Kapitel 3
Deskriptive (beschreibende)
Statistik
Ziel
Beschreibende Statistik besteht in der Aufbereitung, Darstellung und Analyse gesammelter Daten. Die Daten gehören zu einer Vollerhebung (Volkszählung)
oder - viel häufiger - zu einer Stichprobe.
Man unterscheidet zwischen quantitativen und qualitativen Daten.
1. quantitative Daten
Diese werden in diskrete (z.B. Noten einer Prüfung, Anzahl Studenten)
und kontinuierliche Daten (Grösse, Gewicht) unterschieden.
2. qualitative Daten
Hier unterscheidet man nominale Daten (z.B. Haarfarbe, Tierart), wo keine sinnvolle Zuordnung zu Zahlen möglich ist und ordinale Daten (z.B.
hervorragend, gut, usw.). Letztere beziehen sich normalerweise auf eine
grösser/kleiner Relation (Mohs’sche Härteskala). Eine Zuordnung zu Zahlen ist möglich.
3.1
Datenerfassung
Typischerweise wird nicht eine Vollerhebung der Daten durchgeführt, sei es aus
Kostengründen oder auch weil die Gesamtheit schlichtweg nicht bekannt ist;
z.B. alle hochbegabten Kinder.
Daher wird häufig eine repräsentative Stichprobe ausgewählt und es wird
danach aus den Eigenschaften der Stichprobe auf die Eigenschaften der Grundgesamtheit geschlossen. Eine repräsentative Stichprobe auszuwählen ist nicht
immer einfach zu realisieren.
Im folgenden sind die Voraussetzungen für eine repräsentative Stichprobe
zusammengestellt:
17
18
KAPITEL 3. DESKRIPTIVE (BESCHREIBENDE) STATISTIK
• Die Stichprobe ist homogen
• Es liegen gleiche Produktionsbedingungen für die Stichprobe und die Grundgesamtheit vor
• Das Fertigungsverfahren wird und wurde nicht geändert, der Prozess wurde nicht gestört
Eine repräsentative Stichprobe erfordert, dass alle Vertreter der untersuchten
Population (z.B. Tieren, Pflanzen, Menschen) mit der gleichen Wahrscheinlichkeit in der Stichprobe vertreten sind. Dies kann einerseits dadurch erreicht werden, dass die Stichprobe vollkommen zufällig gezogen wird. Gerade bei kleinen
Stichprobengrössen kann jedoch eine solche zufällige Stichprobe zur Über- oder
Unter-Repräsentierung bestimmter Teilpopulationen führen. Zur Lösung dieses
Problems werden oftmals geschichtete (= stratifizierte) Zufalls-Stichproben gezogen, wobei zunächst festgelegt wird, welche Teilpopulationen zu welchen Anteilen in der Stichprobe vertreten sein sollen. Innerhalb dieser Teilpopulationen
werden die Stichproben dann zufällig gezogen.
3.2
Datenbearbeitung
Beispiel
Wir betrachten mehrere Würfe mit 2 Würfeln und zählen die Gesamtzahl
der Augen. Typischerweise werden dann in einer Tabelle die Häufigkeit der verschiedenen Ereignisse eingetragen. Dies kann relativ oder absolut erfolgen. Eine
andere etwas weniger gebräuchliche Darstellung ist die kumulierte Häufigkeit
oder Summenkurve. Dabei werden die Ereignisse, die einen kleineren oder gleichgrossen Wert einnehmen als die Zahl angegeben.
Beispiel: In der unteren Tabelle werde 7 Mal eine kleiner oder gleichgrosse Zahl
als 3 geworfen.
Augenzahl
absolut
relativ
abs. kum.
rel. kum.
2
2
0.02
2
0.02
3
5
0.05
7
0.07
4
5
0.05
12
0.12
5
10
0.10
22
0.22
6
15
0.15
37
0.37
7
21
0.21
58
0.58
8
13
0.13
71
0.71
9
9
0.09
80
0.80
10
8
0.08
88
0.88
11
7
0.07
95
0.95
graphische Darstellung
Für die Darstellung der Daten existieren verschiedene Möglichkeiten. Erwähnt
seien Stabdiagramm, Säulendiagramm (Histogramm) und Kuchendiagramm.
Die Höhe des Stabs bzw. die Fläche der Säule oder des Kuchenstücks Nr. j
entspricht der absoluten oder der relativen Häufigkeit (häufig in %). Die Daten
können natürlich auch durch die kumulierte Häufigkeit dargestellt werden.
In der Abbildung 3.1 wird die absolute und die absolute kumulierte Häufigkeit als Stabdiagramm dargestellt.
12
5
0.05
100
1
3.3. KLASSIERUNG
19
100
20
80
60
Prozent
rel. Haeufigkeit
15
10
40
5
20
0
0
2
3
4
5
6
7
8
Anzahl Augen
9
10
11
12
2
3
4
5
6
7
8
Anzahl Augen
9
10
11
12
Abbildung 3.1: Links ist die absolute Häufigkeit als Stabdiagramm dargestellt
und rechts die absolute kumulierte Häufigkeit des Beispiels der Augenzahl mit
2 Würfeln.
3.3
Klassierung
Falls eine kontinuierlichen Messgrösse betrachtet wird, z.B. die Masse oder die
Grösse von Personen, dann bringt eine solche Häufigkeitstabelle nichts, da jeder
Wert typischerweise nur einmal auftritt.
Histogramme sind gleichwohl eine effiziente und gebräuchliche Methode, um
Verteilungen von kontinuierlichen Variablen zu beschreiben. Im Allgemeinen
stellen Histogramme die Häufigkeit des Auftretens einer Beobachtung innerhalb
gegebener Intervalle gleicher Breite dar. Histogramme können als eine Art Klassifikation von Daten betrachtet werden. Jeder Datenpunkt wird, abhängig von
seinem Wert, in eines der Intervalle sortiert.
Eine wichtige Frage ist die Zahl der Intervalle, die für ein Histogramm verwendet werden soll. Falls die Zahl der Klassen zu niedrig oder zu hoch ist, könnte
das Histogramm die Information in den Daten verdecken.
Als Faustregel gilt,
√
dass man für einen Datensatz mit n Daten in etwa n Klassen verwendet.
Beispiel
Man untersucht das Gewicht von Schülern in einer Klasse. Die folgende
Aufzählung gibt die Masse der verschiedenen Schüler in kg an: 23, 26, 25, 27,
25, 26, 24, 28, 35, 34, 29, 29, 35, 36, 34, 35, 37, 31, 30, 31
√
Es sind 20 Schüler und daher sollten in etwa 20 = 4.47 ∼ 4−5 HistogrammKlassen verwendet werden. Die unterste Grenze sollte 23 kg und die oberste
Grenze 37 kg beinhalten. Die Breite eines Intervalls ist dann gegeben durch
37.5−22.5
= 3. In der unten stehenden Tabelle sind die absolute Häufigkeit und
5
die dazugehörigen Intervalle angegeben. Typischerweise wird als Repräsentant
des Intervalls die Intervalmitte angegeben.
20
KAPITEL 3. DESKRIPTIVE (BESCHREIBENDE) STATISTIK
Intervall
Repräsentant abs. H.
[22.5, 25.5) 24
4
[25.5, 28.5) 27
4
[28.5, 31.5) 30
5
[31.5, 34.5) 33
2
[34.5, 37.5) 36
5
Die Verteilung solcher Daten wird in einem Histogramm dargestellt. Die kumulierte Verteilungsfunktion ist eine Treppenfunktion mit Sprungstellen beim
kleinsten prinzipiell möglichen Wert einer Klasse.
Anmerkungen
1. Werden ungleich breite Klassen verwendet, so ist unbedingt darauf zu
achten, dass nicht die Höhe der Säule sondern deren Fläche der Häufigkeit
entspricht.
2. Man nütze die Freiheiten um ein möglichst schönes Histogramm zu erhalten. Unschön kann z.B. sein, dass leere Klassen existieren. Die Freiheiten
bestehen in der Anzahl der Klassen sowie oft in der Wahl freier Stellen an
den Rändern.
3.4
3.4.1
Lagemass für ordinalskalierte Daten
Median
Definition 3.1 (Medianwert)
Der Median Q50 ist derjenige Wert, der die der Grösse nach aufsteigend geordnete Daten in zwei gleich grosse Werteintervalle teilt; oberhalb wie unterhalb
des Median liegen also 50% der Daten. Zur Berechnung des Medianwertes muss
zwischen einer geraden und einer ungeraden Anzahl Daten xi unterschieden
Werten.
Für n ungerade gilt, dass Q50 = xk mit k = n+1
2 . Falls n gerade ist, so ist der
xn/2 +xn/2+1
Median durch Q50 =
definiert.
2
Beispiele
1. x = {3, 4, 5, 6, 7}, dann ist der Median Q50 = 5.
2. x = {3, 4, 5, 6}, dann ist der Median Q50 =
4+5
2
Es gibt sehr viele verschiedene Definitionen des Medianwertes, alle sind mehr
oder weniger gleichwertig.
3.5. LAGEMASS FÜR METRISCH SKALIERTE DATEN
3.4.2
21
Quantile
Falls man das Prinzip des Medianwertes verallgemeinert, kommt man zum Begriff des Quantils.
Definition 3.2 (Quantil)
Das α%-Quantil Qα ist derjenige Wert, der die der Grösse nach aufsteigend
geordnete Daten so teilt, dass α% der Werte unterhalb von Qα liegen bzw.
(100−α)% oberhalb. Die Berechnung ist ähnlich zu derjenigen des Medianwertes.
Sei n die Anzahl der Daten.
Fall 1: k = n · α/100 ist eine ganze Zahl, dann ist Qα = xk+12+xk
Fall 2: k = n · α/100 ist keine ganze Zahl, dann schneide man von k die Nachkommastellen ab und mit diesem neuen k ′ ist: Qα = xk′ +1 .
Achtung
1. In der Literatur gibt es verschiedenste Definitionen des Quantils. Die oben
genannte ist nur eine davon. Daher kann es sein, dass bei Verwendung
eines Programms (z.B. Excel) die erhaltenen Werte nicht mit dem durch
das oben genannte Verfahren erhaltenen übereinstimmen.
2. In Programmen wird häufig anstatt α in % auch einfach die mehr mathematische Notation 100% =
b 1 verwendet.
Beispiel
Beispiel 1 von oben. Q25 = 4 oder Q20 = 3.5
Anmerkungen
1. Die 25%- Quantile wird auch 1.Quartile genannt.
2. Der Medianwert ist identisch mit Q50 und der 2.Quartile.
3. Die 75%- Quantile wird auch 3 Quartile genannt.
3.5
Lagemass für metrisch skalierte Daten
Die Verteilung der Daten kann durch Kennzahlen charakterisiert werden, welche
die Lage und die Streuung beschreiben. Die wichtigsten Kennzahlen sind der
Mittelwert und die empirische Varianz.
Definition 3.3 (Mittelwert)
Seien n Messwerte gegeben durch xi mit i = 1 . . . n. Dann ist der Mittelwert
n
P
gegeben durch x̄ = n1
xk . Es wird häufig das Symbol µ für den Mittelwert
benutzt.
k=1
22
KAPITEL 3. DESKRIPTIVE (BESCHREIBENDE) STATISTIK
Anmerkungen
Fasst man alle gleichen Ereignisse xi zusammen, so ergibt sich die folgende
Gleichung für die Berechnung des Mittelwertes.
x̄ =
1
n
l
P
hk yk , wobei die hi die absolute Häufigkeit des Ereignisses yi ist.
k=1
Die Ereignisse yk müssen disjunkt sein und alle Ereignisse von xi enthalten.
Falls alle Ereignisse xk verschieden sind, so gilt yi = xi und hi = 1. Das obige
Resultat kann nochmals umgeformt werden.
x̄ =
l
P
p(yk )yk . Hier ist p(yk ) die empirische Wahrscheinlichkeit, dass das
k=1
Ereignisses yk eintritt.
Beispiel
Wir werfen einen Würfel 9 mal und erhalten die Augenzahlen 3, 3, 2, 3,
2, 2, 1, 2, 6. Wie wahrscheinlich ist es, dass die Zahl 4 nie gewürfelt wurde,
falls man annimmt, dass alle Zahlen die gleichgrosse Wahrscheinlichkeit haben?
(p = 0.161)
Dies ergibt einen Mittelwert der Anzahl Augen von x̄ = 3.9. Den Mittelwert kann man nun aber auch mittels der hi und der p(yi ) berechnen. Wir
definieren zuerst die y1 = 1, y2 = 2 . . . , y6 = 6. Also y1 entspricht dem Ereignis, dass der Würfel die Zahl 1 zeigt. Die verschiedenen hi sind dann durch
h1 = 1, h2 = 4, h3 = 3, h4 = 0, h5 = 0, h6 = 1 gegeben. Die p(yi ) sind dann
durch hi /n gegeben. Ich gebe hier nur den Wert für p(y1 ) = 91 an. Natürlich
erhält man mit allen Methoden den gleichen Mittelwert.
Die letzte Definition des Mittelwerts wird auch gewichteter Mittelwert genannt. Die praktische Anwendung des gewichteten Mittelwertes ist vielfältig.
Beispiel
Berechnung des Gebiets-Niederschlages auf der Basis punkthafter Niederschlagsmessungen an Messstationen. Nehmen wir an, dass 4 Messstationen den
Niederschlag für ein gewisses Gebiet repräsentativ messen.
Messstation
A
B
C
D
Summe
Mittelwert
gew. Mittelwert
Messwert
[mm]
21
18
20
4
63
15.8
16.1
Umgebung
[km2 ]
7
6
4
5
22
p(yi )
0.318
0.273
0.182
0.227
1
3.6. STANDARDISIEREN
23
weitere Definitionen
• Modalwert: das ist der wahrscheinlichste Wert. Dies bedeutet, dass der
Wert die grösste Wahrscheinlichkeit besitzt. In einem Histogramm ist dies
also der höchste Balken.
• empirische Varianz
k
1 P
hj (yj − x̄)2 =
s2x = n−1
j=1
n
n−1
k
P
j=1
p(yj )(yj − x̄)2
Dass man durch n − 1 dividiert hat mit der Anzahl Freiheitsgraden zu
tun, wir werden später darauf zurückkommen.
p
Die empirische Standardabweichung ist dann durch sx = s2x gegeben.
• α−Quantile ist genau gleich definiert, wie bei den ordinalskalierten Daten.
• Spannweite = Differenz zwischen dem maximalen und dem minimalen
Wert
• Quartilsabstand = Differenz zwischen dem 1. Quartil und dem 3.Quartil
3.6
Standardisieren
transformiert (x̄ ist der Mittelwert), so besitzen
Werden die xi auf zi = xis−x̄
x
die zi einen Mittelwert von 0 und eine empirische Varianz von 1. Dies ist sehr
nützlich falls man zeigen möchte, dass eine Datenmenge eine gewisse Häufigkeitsverteilung besitzt.
Beispiel
Zeige, dass durch das Standardisieren der Mittelwert 0 und die empirische
Varianz 1 ist.
Lösung
xi −x̄
und damit berechnet sich der Mittelwert
s
x
n
n
P
P
xi
1
n·x̄
x̄
= n1 n·x̄
= 0. Man
−
n
sx
sx
sx − sx
i=1
i=1
2
n n
P
P
2
xi −x̄
1
1
= (n−1)s
(xi − x̄) = 1
2
(n−1)
sx
x
i=1
i=1
Es gilt also zi =
n P
xi −x̄
z̄ = n1
=
sx
i=1
Varianz s2x =
3.7
von zi zu
erhält die
Zusammenfassung
Ein paar Fragen.
1. Es existieren 2 grundsätzlich verschiedene Arten von Daten, welche sind
dies?
2. Welche Probleme können bei der Datenerfassung auftreten?
3. Bei der Datenbearbeitung muss zwischen 2 Arten der Daten unterschieden
werden, welche sind dies?
24
KAPITEL 3. DESKRIPTIVE (BESCHREIBENDE) STATISTIK
4. Welche Art der Darstellung von Daten kennen sie?
5. Wieviele Klassen benutzen sie, falls sie n Daten besitzen?
Versuchen sie in der nächsten Tabelle die entsprechenden Lagemasse für
metrischskalierte Daten einzutragen.
für ordinalskalierte Daten
für metrischskalierte Daten
Medianwert
α−Quantile
Quartile
6. Was ist der Modalwert?
7. Was ist die empirische Varianz?
8. Wo kann die Standardisierung Sinn machen?
Kapitel 4
Verteilungen
4.1
Diskrete Verteilungen
Beispiel
Wir werfen eine Münze und ordnen dem Resultat eine Zahl zu. Zum Beispiel
sei X=1, falls man Kopf und X=0, falls man Zahl geworfen hat. Nun können
wir das Ereignis des Werfens einer Münze mit Hilfe von Zahlen schreiben. So
eine Zuordnung wird Zufallsvariable genannt. Wir können auch die Wahrscheinlichkeit für so ein Ereignis angeben. Dies wird mit der folgenden Notation
geschrieben.
Die Wahrscheinlichkeit das Kopf geworfen wird ist gleich p(X = 0) =
für Zahl p(X = 1) = 21 .
1
2
und
Beispiel Würfeln mit 2 Würfeln
Wir definieren die Zufallsvariable X als Anzahl der Augen und die Ereignisse
Ai = i + 1, i = 1, . . . , 11 (mit 2 Würfeln kann man die Werte 2 bis 12 würfeln).
11
P
p(X = Ai ) = 1
Es gilt nun, dass man mit Sicherheit eine dieser Zahlen wirft
j=1
(∪Ai = Ω, Ai sind disjunkt).
Jeder dieser Werte besitzt eine eigene Wahrscheinlichkeit, wie häufig dieser geworfen wird. Wir berechnen nun für jede mögliche Anzahl Augen diese Wahrscheinlichkeit.
Dazu benutzt man die Laplace Annahme und zusätzlich, dass gewisse Ereignisse
disjunkt und andere unabhängig sind.
Wir berechnen dabei die Anzahl Möglichkeiten eine Zahl zu würfeln. z.B. wir
haben die folgenden Möglichkeiten die Zahl 5 zu würfeln.
{1|4, 2|3, 3|2, 4|1}. Daher ist die Wahrscheinlichkeit eine 5 zu würfeln gleich
5
p(X = 5) = 36
.
Diese Zuordnung der Ai zu den Wahrscheinlichkeiten wird Wahrscheinlichkeitsverteilung genannt.
In der Praxis wird oft versucht, eine empirische Verteilung mit der Vertei25
26
KAPITEL 4. VERTEILUNGEN
lung eines Modells zu vergleichen. Die beiden werden praktisch gleich untersucht,
aber es werden zum Teil andere Bezeichnungen benutzt.
Modellverteilung mit m Ereignissen
Wahrscheinlichkeitsverteilung p(X = Aj )
m
P
p(X = Aj )Aj
Erwartungswert E(X) =
m
P
j=1
j=1
2
p(X = Aj ) (Aj − E(X))
p
Standardabweichung σ = V ar(X)
Varianz V ar(X) =
j=1
Beispiel
Stichprobe vom Umfang n mit m Ereignissen
Experimentelle Verteilung mit pk = hnk
m
P
pj xj
Arithmetischer Mittelwert x̄ =
s2x
n
n−1
pj (xj − x̄)2
p
empirische Standardabweichung sx = s2x
empirische Varianz
=
j=1
Wir betrachten wieder das obige Beispiel des Werfens von 2 Würfeln. Der
Erwartungswert ist, dann gegeben durch
1
E(X) = 36
(1·2+2·3+3·4+4·5+5·6+7·6+8·5+9·4+10·3+11·2+12·1) = 7
und die Varianz ist gegeben durch V ar(X) = 35
6 = 5.83. Daraus erhält man eine
q
35
Standardabweichung von σ =
6 = 2.42.
4.1.1
Uniforme Verteilung
Definition 4.1 (Uniforme Verteilung)
Bei einer uniformen Verteilung sind alle Ereignisse gleich wahrscheinlich.
Beispiel
Berechne den Erwartungswert und die Varianz der Augenzahl beim Würfeln
mit einem Würfel.
Jede der Zahlen ist gleich Wahrscheinlich p = 16 . Damit berechnet sich der
6
P
j · 16 = 3 + 12 und die Varianz zu V ar(X) =
Erwartungswert zu E(X) =
j=1
6
P
j=1
1
6
j− 3+
4.1.2
1
2
2
=
m
P
35
12
Binomialverteilung B(n,p)
Beispiel
Wir werfen eine Münze n-Mal und fragen uns wie gross die Wahrscheinlichkeit ist k-Mal Kopf zu erhalten. Wie wir gesehen haben ist die Wahrscheinlichkeit eines solchen Ereignisses (die Reihenfolge spielt keine Rolle)
n
p(X = k) = B(n, p) =
pk (1 − p)n−k
k
Wobei die Wahrscheinlichkeit Kopf zu werfen p und die Wahrscheinlichkeit
Zahl zu werfen 1 − p ist.
4.1. DISKRETE VERTEILUNGEN
27
0.25
0.35
0.3
0.2
0.25
0.15
p
p
0.2
0.15
0.1
0.1
0.05
0.05
0
0
10
9
8
7
6
5
4
3
2
1
10
9
8
7
6
5
4
3
2
1
Anzahl Kopf
Anzahl Kopf
Abbildung 4.1: Stabdiagramm von zwei Binomialverteilungen (symmetrisch und
links schief)
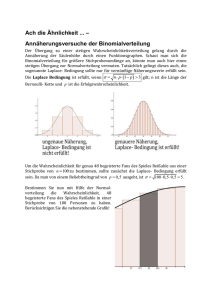
Falls p < 0.5 ist, ist die Verteilung links schief
Falls p = 0.5 ist, ist die Verteilung vollkommen symmetrisch
Falls p > 0.5 ist, ist die Verteilung rechts schief
Die Kennzahlen der Verteilung ergeben sich zu E(X) = np und V ar(X) =
np(1 − p).
Anwendungen
• Wahrscheinlichkeitsberechnung von 2 disjunkten Ereignissen
• Ziehen mit Zurücklegen aus einer Grundgesamtheit
• Wiederholtes Werfen einer Münze
• Verteilungen zur Reinigung von Gemischen (Extraktion)
Anmerkung:
Aus der Verteilung ergibt sich die folgende Beziehung
n X
n
pk (1 − p)n−k = (p + (1 − p))n = 1
k
k=0
Beispiel
1. Wir werfen eine Münze, welche die Wahrscheinlichkeit Kopf (K) zu erhalten p = 0.4 hat und q = 1 − p = 0.6 Zahl (Z) zu erhalten. Die Wahrscheinlichkeiten sind dann gegeben durch:
KK
KZ
ZZ
2
0.42 (1 − 0.4)(2−2) = 0.16
2 2
p=
0.41 (1 − 0.4)(2−1) = 0.48
1
2
p=
0.40 (1 − 0.4)(2−0) = 0.36
0
p=
Sie können dies mit dem Resultat vom Beispiel zum Ereignisbaum vergleichen.
28
KAPITEL 4. VERTEILUNGEN
2. Man kann die Binomialverteilung auch zur Beschreibung irgendeiner Chromatographie benutzen, sei es GC, HPLC usw.
Betrachten wir dazu ein paar Scheidetrichter, welche hintereinander geschaltet sind. Wir benutzen zur Extraktion Essigester und Wasser. Wir
bestimmen das Lösungsgleichgewicht und bemerken, dass von einer Substanz A pA = 0.6 in der Essigesterphase und von einer anderen Substanz
B pB = 0.45 in der Essigesterphase ist. Nun stellen wir eine Reihe von
Scheidetrichter (n=200) auf und wollen wissen, wo die Substanz nach 100
maligen schütteln ist, falls der Essigester von Scheidetrichter 1 zu 2 resp.
2 zu 3 usw. weitertransportiert wird.
Wir können nun den Erwartungswert und die Varianz für die beiden Substanzen getrennt berechnen.
Substanz
A
B
E(X)
E(X) = pA n = 60
E(X) = 45
V ar(X)
√
V ar(X) = npA (1 − pA ) =
24
⇒
σ
=
24
√
V ar(X) = 24.75 ⇒ σ = 24.75
Wir kommen später nochmals auf dieses Beispiel zurück.
4.1.3
Poissonverteilung
Die Poissonverteilung beschreibt die absolute Häufigkeit, mit welcher ein Ereignis in einem bestimmten Zeitintervall τ auftritt. Voraussetzung ist, dass die
Ereignisse unabhängig voneinander sind und mit einer im Mittel konstanten
Rate λ pro Zeitintervall τ eintreten.
Pλ (X = k) =
λk e−λ
k!
Die Kennzahlen sind E(X) = λ und V ar(X) = λ
Anwendungen
• Das sicher bekannteste Beispiel ist der radioaktive Zerfall. Die Zerfälle der
Atome sind vollkommen unabhängig voneinander.
• Es treffen pro Minute λ Meteoriten auf die Erdatmosphäre. Wie gross ist
die Wahrscheinlichkeit, dass in einer Minute k Meteoriten auf die Atmosphäre treffen?
Beispiel
1. An einer Kreuzung ereignen sich im Mittel 0.4 Unfälle pro Monat. Mit
welcher Wahrscheinlichkeit ereignet sich auf diesem Strassenstück mehr
als 1 Unfall in einem Monat?
Wir nehmen an, dass alle Unfälle völlig zufällig und unabhängig voneinander sind. Damit sind die Bedingungen für die Poissonverteilung erfüllt. Der
4.2. KONTINUIERLICHE VERTEILUNGEN
29
Erwartungswert der Poissonverteilung ist λ, daher ist λ = 0.4 für einen
Monat. Die Wahrscheinlichkeit, dass sich mehr als 1 Unfälle ereignen ist
gleich p = 1 − P0.4 (X = 0) − P0.4 (X = 1) = 0.062
2. Eines der klassischen Beispiele für die Poisson-Verteilung ist die Anzahl
der Kavalleristen der preussischen Armee, die durch Hufschlag getötet
wurden. Bei zehn Truppenteilen gab es in 20 Jahren die folgenden Anzahlen von Toten pro Jahr und Truppenteil.
Anzahl der getöteten Soldaten
0
1
2
3
4
Summe
Anzahl der Truppenteil-Jahre
109
65
22
3
1
200
Man berechnet einen Mittelwert pro Jahr von
x̄ =
1
(0 · 109 + 1 · 65 + 2 · 22 + 3 · 3 + 4 · 1) = 0.61
200
Da E(X) = λ bei der Poissonverteilung ist 0.61 eine Schätzung von λ.
Man erhält mit diesem λ die folgende Anzahl der getöteten Soldaten.
Anzahl der getöteten
0
1
2
3
4
Summe
Anzahl der Truppenteile aus der Poissonverteilung
108.7
66.3
20.1
4.1
0.6
199.9
Man sieht also, dass die Abweichungen marginal sind.
4.2
Kontinuierliche Verteilungen
Beispiel
Bei einem Gas hat jedes Gasteilchen eine eigene Geschwindigkeit. Man kann
sich nun fragen wie gross die Wahrscheinlichkeit ist, dass ein Gasteilchen einen
gewissen Betrag der Geschwindigkeit (oder Energie) besitzt. Der Betrag der
Geschwindigkeit ist eine kontinuierliche Grösse, dadurch ist die Wahrscheinlichkeitsverteilung grundsätzlich verschieden von denjenigen der vorherigen Beispiele. Diese Verteilung ist nun eine Funktion auf den positiven Zahlen. Eine solche
Funktion f (x) (diese kann auch auf ganz R definiert sein) heisst Wahrscheinlichkeitsdichte. Die Wahrscheinlichkeitsdichte muss die folgenden Eigenschaften
besitzen.
Wir nehmen an, dass die Wahrscheinlichkeitsdichte (siehe Abbildung 4.2) im
Intervall [a, b] definiert ist. Als Eselsleiter soll man beachten, dass bei alle Definitionen der diskreten Statistik das Summenzeichen durch das Integralzeichen
30
KAPITEL 4. VERTEILUNGEN
y
y = f (x)
p(x < b)
b
x
Abbildung 4.2: Die Darstellung einer Wahrscheinlichkeitsdichte.
zu ersetzten ist.
Eigenschaften der Wahrscheinlichkeitsdichte
1. f (x) ≥ 0 , ∀ x ∈ [a, b]. Warum ist dies so?
2.
Rd
f (x)dx ist die Wahrscheinlichkeit, dass die Zufallsvariable einen Wert
c
zwischen c und d annimmt.
3.
Rb
f (x)dx = 1, Sicherheit einen Wert zwischen a und b zu erhalten.
a
4. Die kumulierte Wahrscheinlichkeit ist gegeben durch F (c) :=
Rc
f (x)dx,
a
wobei a die untere Grenze des Definitionsbereiches von f (x) ist.
5. Die α-Quantile ist derjenige Wert x̃, für welchen gilt α = F (x̃). Also ist
die Grösse der Fläche welche links von x̃ liegt genau α.
6. E(X) =
Rb
xf (x)dx ist der Erwartungswert (Mittelwert).
a
7. V ar(X) =
Rb
f (x)(x−E(x))2 dx. Man sollte sich darunter die durchschnitt-
a
liche Abweichung vom Mittelwert vorstellen.
8. Erwartungswert irgendeiner Funktion g(x) ist gleich E(g(X)) =
Rb
g(x)f (x)dx
a
Im folgenden betrachten wir verschiedene Beispiele von kontinuierlichen Verteilungen.
4.2. KONTINUIERLICHE VERTEILUNGEN
4.2.1
31
Uniforme Verteilung
Die Wahrscheinlichkeitsdichte sei auf einem Intervall überall gleich gross und
sonst 0.
(
1
, falls x ∈ [µ − δ, µ + δ],
p(x) = 2δ
0, sonst
Im folgenden sind die Kennzahlen dieser Wahrscheinlichkeitsdichte angegeben.


0, falls x < µ − δ
2
F (x) = (x−µ+δ)
, für x ∈ [µ − δ, µ + δ] , E(X) = µ, V ar(X) = δ3
2δ


1, falls x > µ + δ
Man kann auch die α Quantile dieser Verteilung ausrechnen. Das heisst α
Prozent liegen links vom Wert x̃(α). Man muss also die Gleichung F (x̃) = α
nach x̃ auflösen.
(x̃ − µ + δ)
= α ⇒ 2αδ − δ + µ
2δ
Beispiel
1. Wie gross ist die Wahrscheinlichkeit, falls man völlig zufällig eine Zahl
zwischen 0 und 1 wählt, dass diese zwischen 14 und 34 liegt?
Intuitiv sollte klar sein, dass die Wahrscheinlichkeit durch p = 12 gegeben
ist. Da alle Zahlen gleich wahrscheinlich gezogen werden ist die Wahrscheinlichkeitsdichte gegeben durch p(x) = 1. Kontrolliere, ob dies eine Wahrscheinlichkeitsdichte ist! Dann ist die Wahrscheinlichkeit gegeben
durch
3
Z4
1
p = 1dx =
2
1
4
2. Man möchte wissen, wie gross die Wahrscheinlichkeit bei einem gleichschenkligen Dreieck ist, dass die Seite s länger ist als diejenige der gleichen
Schenkel d (Siehe Abbildung 4.3).
(a) Lösung 1
Wie wir wissen, liegt die Grenze zwischen grösser und kleiner bei
einem Öffnungswinkel von 60◦ . Man kann den Winkel von 0◦ bis 180◦
wählen. Somit ist die Wahrscheinlichkeit, dass die Seite s grösser als
60
d ist gegeben durch p = 1 − 180
= 32 .
(b) Lösung 2
Wir zeichnen nun einen Kreis mit Radius 1 und definieren, dass die
obere Spitze des Dreiecks am höchsten Punkt dieses Kreises liegt, wie
in der Abbildung 4.3 rechts. Nun definieren die Schnittpunkte der
gleichen Schenkel mit dem Kreis eine horizontale Linie, zusammen
32
KAPITEL 4. VERTEILUNGEN
}
D
d
d
s
Abbildung 4.3: Wie gross ist die Wahrscheinlichkeit, dass die Seite s länger ist
als d.
mit dem obersten Punkt ein Dreieck. Falls D < 23 ist, dann ist s > d.
Somit ist die Wahrscheinlichkeit gegeben durch p = 23 · 12 = 43 .
Was stimmt nun, ist es 32 oder 43 . Man sieht hier, dass es auch auf die
Auswahl (Winkel, Strecke) ankommt.
4.2.2
Maxwell-Boltzmann Verteilung
Die Maxwell-Boltzmann Verteilung gibt die Wahrscheinlichkeit an, dass ein Gasteilchen mit der Molmasse M bei der Temperatur T den Betrag der Geschwindigkeit v besitzt (R ist die Gaskonstante). Die Wahrscheinlichkeitsdichte ist
gegeben durch:
q
v2
M 3/2 2 − M
p(v) = π2 RT
v e 2RT
Diese Wahrscheinlichkeitsdichte besitzt die oben beschriebenen Eigenschaften und ist nur auf den positiven Zahlen v ≥ 0 definiert. In der Abbildung 4.4
ist die Maxwell-Boltzmann Verteilung für Stickstoff bei 25◦ C abgebildet.
Um die folgenden Berechnungen durchzuführen ist es vorteilhaft, die beiden
folgenden Integrale zu kennen (diese können mittels partieller Integration berechnet werden).
R∞
x2n e−x
2
/a2
dx =
0
R∞
0
x2n+1 e−x
2
/a2
√ (2n)!
π n!
dx =
a 2n+1
2
(a2 )n+1
n!
2
Berechne damit folgendes:
4.2. KONTINUIERLICHE VERTEILUNGEN
33
p(v)
E(v)
vh
0
100
200
300
400
500
600
700
800
900
1000
v
Abbildung 4.4: Die Maxwell Boltzmann Verteilung für Stickstoff bei 25◦ C.
1. Zeige, dass
R∞
p(v)dv = 1, d.h die Funktion p(v) ist eine Wahrscheinlich-
0
keitsdichte (mit der Bedingung, dass p(v) ≥ 0).
2. Berechne die Geschwindigkeit, mit welcher die Gasteilchen am häufigsten
im Gas vorkommen.
3. Berechne den Erwartungswert der Geschwindigkeit v.
Im folgenden berechnen wir den Erwartungswert der kinetischen Energie
Ekin = 21 M v 2 .
q
R∞
R∞
E(Ekin ) = 12 M v 2 p(v)dv = 21 M v 2 π2
0
0
q
R∞ 4 −Mv2 /(2RT )
2
M 3/2
1
v e
dv = 23 RT
2M
π 2RT
M 3/2
2RT
v 2 e−Mv
2
/(2RT )
dv =
0
Falls wir also Gasteilchen aus einem Gas herauspicken, so besitzen sie im Mittel
die Energie 23 RT .
4.2.3
Exponentialverteilung
Diese Verteilung folgt aus der Poissonverteilung, wenn als Zufallsvariable die
Dauer bis zum Eintreten des nächsten Ereignisses betrachtet wird. Dabei spielt
es keine Rolle, ob gerade ein Ereignis eingetreten ist oder nicht (Unabhängigkeit).
Beispiel
1. Die Zeit zwischen zwei Zusammenstössen in einem Gas.
2. Besitzen die Zeiten zwischen Erdbeben in einem Gebiet diese Verteilung?
Wie ist es, wenn man die Erdbeben in schwache und starke aufteilt?
(
0, falls x < 0
p(x) =
λe−λx , sonst
34
KAPITEL 4. VERTEILUNGEN
Die Kenngrössen sind hier durch
(
0, falls x < 0
F (x) =
1 − e−λx , sonst
die Variation ist V ar(X) = λ12 , der Erwartungswert E(X) =
α
ln(1− 100
)
Quantile durch x̃(α) = −
gegeben.
λ
4.2.4
1
λ
und die α-
Normalverteilung
Die weitaus wichtigste Verteilung haben wir uns bis zum Schluss aufgespart.
Die Bedeutung dieser Verteilung kommt vom zentralen Grenzwertsatz her.
Dieser sagt aus, dass man von irgendeiner Grundgesamtheit mit irgendeiner
Verteilung (kann auch 2 Maxima besitzen) m Mal den Mittelwert mit n Anzahl Daten bestimmt. Diese verschiedenen Mittelwerte dann den Mittelwert der
Verteilung besitzen und dass ihre Verteilung für den Grenzwert m → ∞, gegen
die Normalverteilung konvergiert. Es spielt dabei keine Rolle ob man z.B. die
Grösse aller Menschen oder nur die von Erwachsenen benutzt. Die statistischen
Kenngrössen unterscheiden sich, aber nicht die Form der Verteilung.
p(x) = √
1
2πσ 2
e−
(x−µ)2
2σ2
Die statistischen Kenngrössen sind durch E(X) = µ (Mittelwert) und
V ar(X) = σ 2 (Standardabweichung) möglichst einfach gegeben. Hier haben wir
einen Fall, bei der die kumulierte Häufigkeit F (X) nicht durch allgemeine Integrationsregeln berechnet werden kann. Diese Funktion ist normalerweise in
Computerprogrammen enthalten und wird dort häufig als Fehlerfunktion bezeichnet. Besser wäre Gauss’sche Fehlerfunktion, da der Begriff Fehlerfunktion
zum Teil auch eine andere Verwendung besitzt.
Frage
Skizzieren Sie die Funktion p(x) oben. Berechnen sie dazu die Extrema (Maxima bei x = µ) und zeigen sie, dass die Funktion bei µ ± σ einen Wendepunkt
(f ′′ (x) = 0 und f ′′′ (x) 6= 0) besitzt.
Eine weitere wichtige Eigenschaft der Normalverteilung ist der Additionssatz. Dieser besagt, dass falls man 2 Zufallsvariablen (X1 und X2 ) hat, welche
normalverteilt sind und die Kenngrössen (µ1 , σ12 ) und (µ2 , σ22 ) besitzen, die Addition und Subtraktion X1 ± X2 dieser beiden Zufallsvariablen auch normalverteilt sind und die Kenngrössen (µ1 ± µ2 , σ12 + σ22 ) besitzen.
Folgerung
q
Für den Mittelwert von n Messungen ergibt sich, dass der Mittelwert mit n1
gegen den Mittelwert der Verteilung konvergiert. Nun sieht man, dass Wiederholungen von Messungen nur bis zu einer gewissen Anzahl Sinn machen.
4.2. KONTINUIERLICHE VERTEILUNGEN
35
1
p(x)
F(x)
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-3
-2
-1
0
1
2
3
x
Abbildung 4.5: Standardnormalverteilung und ihre kumulierte Häufigkeit)
Beispiel
Abschätzungsweise kann die folgende Näherung benutzt werden. Später werden
wir dann noch sehen, dass dies nur eine Näherung ist.
Um die Genauigkeit eines Resultats zu erhöhen kann man mehrere Messungen
hintereinander durchführen.
Anzahl Messungen: 2, Verdoppelung der Genauigkeit des Mittelwertes bei 4 =
22 · 2 Messungen.
Anzahl Messungen: 10, Verdoppelung der Genauigkeit bei 40 = 22 · 10 Messungen.
Standardnormalverteilung
Die Standardnormalverteilung ist die Normalverteilung mit Mittelwert µ = 0
und Standardabweichung σ 2 = 1. Jede Normalverteilung kann durch die Transformation z = x−µ
σ in die Standardnormalverteilung transformiert werden. Diese
Transformation ist vor allem für die kumulierte Wahrscheinlichkeit wichtig, da
in Büchern oft die Werte dieser Funktion tabeliert sind.
Im folgende ist angegeben wieviel Prozent der Werte bei der Standardabweichung innerhalb des Intervalls [−kσ, kσ] (siehe 8.1) liegen.
Intervall
[−σ, σ]
[−2σ, 2σ]
[−3σ, 3σ]
% aller Werte
68.3
95.4
99.7
Dieses Resultat ist wichtig, da es für alle Normalverteilungen mit (µ, σ) gilt.
Wie gross ist die Wahrscheinlichkeit von [0, σ]? ( 68.3
2 = 34.15)
36
KAPITEL 4. VERTEILUNGEN
Extraktion
0.09
Substanz A
Substanz B
0.08
0.07
0.06
p
0.05
0.04
0.03
0.02
0.01
0
0
20
40
60
80
100
Gefäss
Abbildung 4.6: Beispiel der Extraktion von 2 Substanzen. Die Trennung ist noch
nicht gut.
4.3
Zusammenhang zwischen den verschiedenen
Verteilungen
Die Poissonverteilung und auch die Gaussverteilung sind Spezialfälle der Binomialverteilung. Es ist viel einfacher mit der Gaussverteilung oder der Poissonverteilung als mit der Binomialverteilung zu rechnen, daher haben diese ihre
Berechtigungen.
In der folgenden Tabelle sind die Bedingungen aufgestellt unter welchen die
Binomialverteilung durch die Gaussverteilung oder die Poissonverteilung angenähert werden kann.
Bedingung
Falls p < 0.05 und n > 10
Falls np(1 − p) > 9
Näherung durch
Poissonverteilung mit λ = np
Gaussverteilung mit µ = np und σ 2 = np(1 − p)
Beispiel
1. Wir betrachten wieder das Beispiel der Extraktion. Nun können wir ohne
Probleme mithilfe der Gaussverteilung die Graphen 4.6 zeichnen und auch
die Trennung der Substanzen abschätzen. Um die Trennung abschätzen zu
können, berechnen wir ob sich die Intervalle in welchen 95% der Substanz
A resp. B sind, überschneiden. Man erhält für Substanz A [50, 70] und für
Substanz B [35, 55]. Man könnte sich fragen, wieviel Extraktionen man machen muss, damit sich die 99.7% Intervalle nicht überschneiden. (Lösung:
n = 390).
2. Man habe einen Münzwurf mit der Wahrscheinlichkeit p = 0.01 Kopf zu
erhalten.Wie gross ist dann die Wahrscheinlichkeit 10 Mal Kopf zu werfen,
4.3. ZUSAMMENHANG ZWISCHEN DEN VERSCHIEDENEN VERTEILUNGEN37
falls man die Münze 1000 man wirft?
Mit der Binomialverteilung: p(10) = 0.12574
Mit der Poissonverteilung: p(10) = 0.12511
3. Betrachten wir noch einmal die Kreuzung auf welcher sich im Mittel 0.4
Unfälle pro Monat ereignen.
Wir nehmen nun an, dass sich in einem Monat ein Unfall ereignet mit
Wahrscheinlichkeit p = 0.4, dann stimmt der Erwartungswert dieser Verteilung mit der Wirklichkeit überein, aber es kann auch mehr als 1 Unfall
passieren, welches durch diese Verteilung nicht beschrieben wird.
Um das ganze zu verbessern teilen wir den Monat in n Zeitintervalle, mit
n → ∞, p = nµ → 0, µ = n · p = 0.4. Solche Ereignisse werden durch eine Binomialverteilung B(n, 0.4
n ) beschrieben. Für n gegen Unendlich konvergiert diese Binomialverteilung gegen die Poissonverteilung pλ=0.4 und
daher ist das Resultat bei der Poissonverteilung korrekt.
38
KAPITEL 4. VERTEILUNGEN
4.4
Zusammenfassung
Die Wahrscheinlichkeitsverteilung gibt an, wie sich die Wahrscheinlichkeiten
auf die möglichen Zufallsereignisse verteilen. Man unterscheidet zwischen der
Häufigkeitsverteilung (empirische Daten) und den Verteilungen aus theoretischen Überlegungen.
Füllen sie in die Tabelle die fehlenden Informationen ein.
Modellverteilung mit m Ereignissen
Wahrscheinlichkeitsverteilung p(X = Aj )
Stichprobe vom Umfang n
Experimentelle Verteilung mit pk =
Erwartungswert E(X) =
Mittelwert x̄ =
Varianz V ar(X) =
emp. Varianz s2x =
hk
n
Ein paar Fragen.
1. Was für diskrete Verteilungen kennen sie? Und geben sie für jede dieser
Verteilungen ein typisches Beispiel an. Wie gross sind die Erwartungswerte
und die Varianz dieser Verteilungen?
2. Welche Bedingungen muss eine Wahrscheinlichkeitsdichte erfüllen?
3. Wie berechnet man den Erwartungswert, die Varianz und die α-Quantile
bei einer Wahrscheinlichkeitsdichte?
4. Was für kontinuierliche Verteilungen kennen sie? Geben sie für jede dieser
Verteilungen ein Beispiel an. Wie gross sind die Erwartungswerte und die
Varianz dieser Verteilungen?
5. Was ist standardisieren?
6. Was ist das spezielle der Gaussverteilung? Wieviel Prozent der Fläche liegt
zwischen µ ± σ, µ ± 2σ und µ ± 3σ?
7. Skizziere die Gaussverteilung.
8. Wie hängen die Binomialverteilung, die Poissonverteilung und die Gaussverteilung zusammen?
-
Kapitel 5
Statistische Tests
Man will hier aus den Daten einer zufälligen Stichprobe Aussagen über Kenngrössen oder auch über die Wahrscheinlichkeitsdichte machen. Die Stichprobe
kann z.B. aus ein paar Exemplaren von Tabletten bestehen (Bestimmung der
Konzentration des Wirkstoffs), welche zufällig entnommen wurden, die Grundgesamtheit ist dann z.B. die Tagesproduktion.
Üblicherweise wird bei den folgenden Tests angenommen, dass die Daten
normalverteilt sind.
5.1
Freiheitsgrade
Um die statistischen Tests zu verstehen, muss der Begriff des Freiheitsgrades
eingeführt werden.
Bei der Berechnung eines statistischen Parameters eines Datensatzes ist es
oft notwendig zunächst ein Zwischenergebnis zu berechnen (z.B. den Mittelwert). Wenn solche Parameter bei der Berechnung berücksichtigt werden, wird
die Zahl der unabhängigen Werte reduziert, da das Zwischenergebnis ja bereits
alle Werte mit einbezieht.
Ein Beispiel soll das erklären: Überlegen Sie sich die Berechnung der empirischen Varianz, die durch Mitteln der Quadrate der Abweichungen vom Mittelwert x̄ berechnet wird.
n
s2x =
1 X
(xk − x̄)2
n−1
k=1
Weil der Mittelwert x̄ von allen Werten bereits berechnet wurde, ist die Anzahl der unabhängigen Werte in der Formel für die empirische Varianz um 1
reduziert (man könnte ja einen der ursprünglichen Werte durch Verwenden des
Mittelwerts und aller anderen Werte berechnen).
Allgemein gesprochen hängen die Anzahl der Freiheitsgrade (F G) von der
Zahl an unabhängigen Beobachtungen ab: F G ist die Zahl der Beobachtungen
n minus der Zahl der berücksichtigen Parameter a,
F G = (n − a) ,
wobei die Wahl der Verteilung auch ein Parameter sein kann.
39
40
KAPITEL 5. STATISTISCHE TESTS
5.2
Schätzer
Im vorherigen Beispiel haben wir schon bemerkt, dass man aus den Daten der
Stichprobe die Kennwerte der Verteilung der Grundgesamtheit nur schätzen
kann. Funktionen, welche das tun, heissen Schätzer. Wir haben schon solche
Funktion angetroffen, nämlich den Mittelwert x̄, der den Erwartungswert der
Verteilung E(X) schätzt. Der Schätzer sollte die folgenden Eigenschaften besitzen.
1. Der geschätzte Wert (Mittelwert x̄ einer Stichprobe mit n Elementen)
sollte für n → ∞ gegen den Erwartungswert E(X) der Grundgesamtheit
konvergieren (erwartungstreu).
2. Die Varianz des Schätzers sollte mit n → ∞ gegen 0 streben(konsistent).
Ein effizienter und konsistenter Schätzer des Erwartungswertes E(X) ist der
arithmetische Mittelwert der Probe. Derjenige für die Varianz ist die Stichprobenvarianz.
5.2.1
Beispiele für verschiedene Schätzer
1. Poissonstatistik
Wir haben im Abschnitt über die Verteilungen gesehen, dass der Mittelwert x̄ ein Schätzer f ür den Parameter λ ist und dass auch die Standardabweichung im Quadrat s2x ein Schätzer für λ ist. Welcher soll man nun
wählen? Ist einer besser als der andere?
Wir möchten einen Schätzer, der bei Messwiederholung möglichst nahe
bei dem Erwartungswert des Schätzer liegt. Dies Abweichung beschreiben
wir am einfachsten mit der Standardabweichung dieser ’identischen’ Messungen.
In den beiden folgenden Graphen sind die Histogramme der Schätzung
von 100000 Experimenten aufgetragen.
Shätzer s2n fuer λ
8000
8000
7000
7000
6000
6000
Häugkeit
Häugkeit
Shätzer x̄ fuer λ
9000
5000
4000
3000
5000
4000
3000
2000
2000
1000
1000
0
0
2
4
6
8
10
λ
Abbildung 5.1: Histogram des Schätzers
x̄ für λ für 105 Experimente
0
0
2
4
6
8
10
λ
Abbildung 5.2: Histogram des Schätzers
s2x für λ für 105 Experimente
5.3. VERTRAUENSINTERVALL
41
2. Federkonstante
Im Physikpraktikum haben wir die Federkonstante einer Feder bestimmt.
Einzelne Studierende wollen die Federkonstante Di = Fxii für jeden einzelnen Messwert der Auslenkung xi bezüglich angewandten Kraft Fi berechnen. Danach möchten sie den Mittelwert der so erhaltenen Schätzer der
Federkonstante berechnen.
Es kann gezeigt werden, dass dieser Schätzer fast immer schlechter ist,
als derjenige der Regression. Dieser Schätzer besitzt eine deutlich grössere
Varianz als derjenige der Regression.
5.3
Vertrauensintervall
Der arithmetische Mittelwert gibt eine Schätzung für den Erwartungswert E(X).
Dies ist aber genau ein Wert. Wir wissen aber, dass die Stichprobe mit grosser
Wahrscheinlichkeit nicht den wahren Wert ausgibt sondern einen Wert nahe des
Erwartungswertes. Man stellt sich nun die Frage: wie weit nach links und rechts
vom Mittelwert aus, erstreckt sich das Intervall, welches mit einer gewissen
Wahrscheinlichkeit (=gewähltes Vertrauensniveau) den wahren Wert enthält.
Dieses Intervall wird Vertrauensintervall genannt.
Wegen des zentralen Grenzwertsatzes liegen ca. 95% der Daten zwischen
µ ± 2 √σn . Dieses Intervall wird 95% Vertrauensintervall (Irrtumswahrscheinlichkeit α = 1 − 0.95) genannt. Nun kennen wir aber σ nicht genau sondern können
dieses nur mittels sx schätzen. In der Praxis kann man bei einer Anzahl Daten
von n > 30 mit sx rechnen. Bei weniger Messungen muss man einen Korrekturfaktor einführen, weil die Standardabweichung der Stichprobe selbst eine
Zufallsvariable ist.
Der Mathematiker Gosset hat die Verteilung dieser standardisierten Mittelwerts
untersucht und unter dem Pseudonym Student veröffentlicht. Sie hängt von n
ab und heisst Student t-Verteilung für n − 1 Freiheitsgrade.
Die Student t-Verteilung geht für n → ∞ in die Normalverteilung über. Um
das σ zu schätzen muss nun die empirische Varianz sx nicht mit dem 1 − α/2Quantil der Standardnormalverteilung, sondern mit derjenigen der Student tVerteilung (siehe 8.2) mit n − 1 Freiheitsgrade multipliziert werden.
Beispiel
Bestimmen Sie das 95%-Vertrauensintervall des folgenden Beispiels. Der arithmetische Mittelwert einer Stichprobe mit n = 8 sei x̄ = 2.11 und die empirische
√
=
Varianz s2x = 1.22 . Dies ergibt ein 95%-Vertrauensintervall von 2.11 ± 1.2·2.365
7
2.11 ± 1.07 (siehe Tabelle der Student t-Verteilung am Schluss des Skripts 8.2
mit tα/2,8−1 = t0.025,7 = 2.365).
42
KAPITEL 5. STATISTISCHE TESTS
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x, dann berechnet t.test(x) das Vertrauensintervall
und gibt es aus.
Eingabe
t.test(x,conf.level=0.975)
Ausgabe
One-Sample t-Test
data:x
Hier Daten, welche dann für den t-Test relevant sind.
97.5 percent confidence intervall:
2803 6002
sample estimates:
mean of x
4360
2. Excel
Hier gibt es 2 Möglichkeiten.
(a) Im Moodle Kurs Hilfsmittel zur Datenanalyse kann das Excel File: 1
Stichprobe metrisch benutzt werden.
(b) Es gibt den Befehl T IN V (α, n − 1) im Excel um den t-Wert zu berechnen.
5.4. HYPOTHESEN-TESTS
5.4
5.4.1
43
Hypothesen-Tests
Hypothese
Mit einem statistischen Test wird beurteilt, ob Daten mit einer Anfangshypothese, der Nullhypothese, vereinbar sind oder Evidenz dagegen liefern und eher
für eine Alternativhypothese sprechen. Hypothesen sind Aussagen über die Verteilung einer Zufallsvariable und/oder über Parameter der Verteilung.
Ein Hypothesentest ist eine Entscheidungsgrundlage. Der P -Wert ist die
Wahrscheinlichkeit, berechnet unter Annahme der Nullhypothese, einen mindestens so extremen Wert der Testgrösse zu erhalten wie derjenige, der beobachtet
wurde. Wenn der P -Wert kleiner als eine vorgegebene Zahl α ist, dann ist der
Test statistisch signifikant auf dem Signifikanzniveau α. Die Nullhypothese
(NH) wird dann verworfen.
Bei einem Hypothesentest sind 4 Varianten denkbar.
NH wird beibehalten
NH wird verworfen
P >α
P ≤α
NH trifft zu
Ok. (p = 1 − α)
Fehler 1.Art (α Fehler) (p = α)
NH trifft nicht zu Fehler 2.Art (β Fehler) Ok! (p = 1 − β wird Power genannt)
Bei einer Irrtumswahrscheinlichkeit von < 5% spricht man von signifikanten
Ergebnissen. Ist die Irrtumswahrscheinlichkeit < 1% spricht man von hochsignifikant.
Bemerkungen
Man sollte darauf achten, dass eine Hypothese eigentlich nicht bewiesen werden
kann, sie kann im mathematisch strengen Sinne nur verworfen werden und dieses auch nur mit einer gewissen Wahrscheinlichkeit.
Beispiel 1
In den folgenden Abbildungen 5.3 ist eine typische Situation eines Hypothesentests anhand eines Mittelwertes dargestellt. Vergesst in einem ersten Schritt
einmal die rechte Glockenkurve im oberen Graphen. Trifft nun die Nullhypothese zu, so liegen bei einer Messwiederholung α Prozent in den beiden grauen
Bereichen (symmetrisch um 0). Man würde in diesem Fall die Nullhypothese
verwerfen, obwohl sie zutrifft. Nehmen wir nun an, dass unsere Probe einen
Erwartunsgwert von µ = 2 besitzt, dann trifft die Alternativhypothese zu. In
diesem Fall ist der β Fehler durch die rote Kurve links neben dem rechten Teil
der den α Fehler repressentierenden Fläche gegeben. In der unteren Grafik ist
die gleiche Situation dargestellt, für den Fall dass der Erwarttungswert der Probe bei 1 liegt. In diesem Fall ist die Trennschärfe des Tests stark verkleinert.
44
KAPITEL 5. STATISTISCHE TESTS
µ1 = 0
α
2
µ2 = 2
β
µ1 = 0
α
2
α
2
µ2 = 1
β
α
2
Abbildung 5.3: Hypothesentest am Beispiel der Mittelwerte. Das obere Beispiel
besitzt eine deutlich bessere Trennschärfe als das untere Beispiel.
Beispiel 2
Betrachten wir 2 Münzen. Eine sei völlig ausbalanciert, was bedeutet, dass die
Wahrscheinlichkeit Kopf zu werfen gleich gross ist wie die Wahrscheinlichkeit
Zahl zu werfen. Die andere Münze besitze eine Wahrscheinlichkeit p = 0.3 Kopf
anzuzeigen und eine Wahrscheinlichkeit 1 − p = 0.7 Kopf anzuzeigen. Falls
wir zufällig eine dieser beiden Münzen nehmen und diese werfen: existiert eine
Möglichkeit, dass wir 100% sicher sein können, welche Münze wir in der Hand
haben?
Die Antwort ist “Nein”. Man müsste die Münze unendlich oft werfen, um dies
mit Sicherheit entscheiden zu können. Berechnen wir einmal ein paar Wahrscheinlichkeiten dazu.
5.5. WELCHER TEST?
45
Beispiele 5.1 Wir Werfen die Münze 3 Mal und möchten nun entscheiden,
welche Münze wir in der Hand haben.
Berechnen wir die Wahrscheinlichkeiten, dass wir 0,1,2,3 Mal Kopf geworfen haben unter den Hypothesen, dass wir die ausgewogene Münze (H0 ) resp.
die nicht ausgewogene Münze (H1 ) in der Hand haben. Dies sind bedingte
Wahrscheinlichkeiten. Man erhält die folgende Tabelle.
Anzahl Zahl p(ω|H0 ) p(ω|H1 )
0
0.125
0.343
1
0.375
0.441
2
0.375
0.189
3
0.125
0.027
Falls wir nun bei einem Experiment 0 Mal Zahl erhalten haben, so ist nach der
obigen Tabelle die Wahrscheinlichkeit grösser, dass die Hypothese H1 eintrifft.
Es kann aber nicht ausgeschlossen werden, dass die Hypothese H0 zutrifft.
Im obigen Fall würden wir also falls wir 0 oder 1 Mal Zahl geworfen haben,
annehmen, dass wir die nicht ausgewogene Münze in den Händen halten. Haben
wir hingegen 2 oder 3 Mal Zahl geworfen, so ist es wahrscheinlicher,dass wir
die ausgewogene Münze in den Händen haben.
Nehmen wir nun als Nullhypothese an, dass wir die ausgewogene Münze in
den Händen haben. Wie gross ist nun die Wahrscheinlichkeit einen Fehler 1.
Art (α- Fehler) zu begehen? Dies bedeutet, dass die NH verworfen wird, obwohl
die NH zutrifft. Diese Wahrscheinlichkeit können wir mithilfe der obigen
Tabelle berechnen. Es ist dies pα = 0.125 + 0.375. Der β-Fehler (die NH wird
beibehalten, obwohl sie nicht zutrifft) kann auch mithilfe der Tabelle berechnet
werden. Dort gilt pβ = 0.189 + 0.027.
Man sieht also, dass der α-Fehler nicht unabhängig vom β-Fehler ist.
5.5
Welcher Test?
Es gibt praktisch unendlich viele Tests. Diese werden auch häufig in grafischer
Form zusammen gestellt, so dass man sich entscheiden kann, welchen Test man
nehmen sollte. In der Abbildung 5.4 ist so ein Entscheidungsbaum abgebildet.
Für die Durchführung der Tests empfehle ich die Statistiksoftware R, welche
frei verfügbar ist. Es gibt aber ein paar kleine Einstiegshürden. Um diese zu
verkleinern, sollte man sich den Moodle Kurs (R-Online Course (Department
Life Science, Übergreifend, Mathematik und Physik)) anschauen.
46
KAPITEL 5. STATISTISCHE TESTS
Abbildung 5.4: Ein möglicher Entscheidungsbaum. Bei den Tests handelt es sich
um eine kleine Auswahl.
5.6. TEST AUF NORMALVERTEILUNG
5.5.1
47
Vorgehensweise
Bei einem statistischen Test, muss man vor dem Experiment schon bewusst
sein,was man Testen will und wie!!
1. Was möchte man Testen?
2. Welche Methode und welche Signifiknazniveau? (Auswege falls Voraussetzungen nicht erfüllt schon im Hinterkopf haben)
3. Auswertung
5.6
Test auf Normalverteilung
Bei sogenannt parametrischen Tests wird häufig benötigt, dass die Daten normalverteilt sind (parametrische Tests). Dies kann man mit verschiedenen Tests
herausfinden. Alle geben typischerweise leicht verschiedene p-Werte an.
Wir betrachten zuerst den QQ-Plot, welcher kein eigentlicher Test ist, aber
eine Methode um grafisch abzuschätzen, ob die Daten normalverteilt sind.
5.6.1
QQ-Plot
Beispiel
Ein Material soll den Volumenaufbau von Weichgeweben im Mund gewährleisten. Das Material wurde im Reaktor mit Zellen besiedelt und anschliessend
unter statischen Bedingungen 14 Tage kultiviert. Danach wurde die Anzahl der
aktiven Zellen auf dem Material gemessen. Man hat 19 verschiedene Proben
hergestellt und ausgemessen.
Man hat die folgenden Messwerte 3211.44, 4038.14, 3226.97, 1239.87, 851.5,
1769.38, 7615.08, 6865.6, 5109.29, 3221.19, 3267.5, 3930.4, 3301.19, 5270.05,
4648.16, 7804.68, 12533.99, 2240.12, 2777.09 erhalten.
Theorie
Bei diesem Test werden die experimentellen Werte (Anzahl aktive Zellen) gegen die theoretische Quantile einer Normalverteilung aufgetragen, um die beiden
Verteilungen zu vergleichen. Dazu ordnen wir zuerst die experimentellen Daten
der Grösse nach und nummerieren sie von 1 bis n durch. Nun wird zu jedem
experimentellen Wert die dazugehörige theoretische α−Quantile der Normalverteilung berechnet. Dazu berechnen wir zuerst aus der Position i die kumulierte
Häufigkeit P (i) von jedem der Grösse nach geordneten Messwert i. Es existieren viele mehr oder weniger äquivalente Methoden dies zu bewerkstelligen, aber
i− 3
wir werden nur eine davon benutzen P (i) = n+81 . Anschliessend wird mit der
4
kumulierten Häufigkeit Pi die α-Quantile der Normalverteilung αtheo berechnet
48
KAPITEL 5. STATISTISCHE TESTS
oder aus einer Tabelle ausgelesen. Werden nun die Messwerte gegen die theoretischen α-Quantilen der Normalverteilung aufgetragen, so müssen die Punkte
auf einer Geraden liegen, falls sie normalverteilt sind. Oft wird die Gerade so
gezeichnet, dass sie durch die 1. und die 3. Quartile geht, dies sind hier die
Punkte (−0.6745, 2994) und (0.6745, 5190).
Anwendung auf das obige Beispiel
Nun sortieren wir die Messewerte der Proben der Grösse nach und nummerieren sie durch. Anschliessend berechnen wir die kumulierte Häufigkeit mittels
i− 3
P (i) = n+81 .
4
Wir besitzen n = 19 Messwerte und für den kleinsten Wert 851.5 ist i = 1
5
≈ 0.03. Anschliessend wird aus der Tabelle die α-Quantile
und damit P (1) = 154
der Normalverteilung ausgelesen zth (1) = −1.85.
Wert
i
P (i) zth
zex
851.5
1
0.03 -1.85 -1.26
1239.87
2
0.08 -1.38 -1.12
1769.38
3
0.14 -1.1
-0.93
2240.12
4
0.19 -0.88 -0.76
2777.09
5
0.24 -0.71 -0.57
3211.44
6
0.29 -0.55 -0.41
3221.19
7
0.34 -0.4
-0.41
3226.97
8
0.4
-0.26 -0.41
3267.5
9
0.45 -0.13 -0.39
3301.19
10 0.5
0
-0.38
3930.4
11 0.55 0.13
-0.16
4038.14
12 0.6
0.26
-0.12
4648.16
13 0.66 0.4
0.1
5109.29
14 0.71 0.55
0.27
5270.05
15 0.76 0.71
0.33
6865.6
16 0.81 0.88
0.9
7615.08
17 0.86 1.1
1.17
7804.68
18 0.92 1.38
1.24
12533.99 19 0.97 1.85
2.94
In der Abbildung 5.5 ist der Wert gegen die theoretische Quantilen aufgetragen und in der Tabelle sind die berechneten Werte enthalten. Es sieht in diesem
Fall nicht so aus, dass die Daten normalverteilt sind. Dies wollen wir aber nun
mit dem Kolmogorov-Smirnov Test quantifizieren.
Anmerkung
Betrachtet man diese Methode ein bisschen genauer, so sieht man direkt, dass
man Daten damit auf eine beliebige Verteilung testen kann. Das einzige was sich
ändert sind die α−Quantile der theoretischen Verteilung. Diese kann man aber
entweder ausrechnen oder aus einer Tabelle auslesen.
5.6. TEST AUF NORMALVERTEILUNG
14000
49
Daten
Linie
12000
Experiment
10000
8000
6000
4000
2000
0
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
zth
Abbildung 5.5: QQ Plot der Daten aus den Versuchen des Gewebeaufbaus.
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x, dann führt qqplot(x) zum Graph und eine Linie
wird mit qqline(x) dazu gebracht.
Befehl
qqplot(x)
qqline(x)
Output
Es wird direkt der benötigte Graph produziert.
2. Excel
Im Moodle Kurs Hilfsmittel zur Datenanalyse kann das Excel File: 1 Stichprobe metrisch benutzt werden.
50
KAPITEL 5. STATISTISCHE TESTS
5.6.2
Kolmogorov-Smirnov Test
Die Nullhypothese ist die, dass die Daten aus einer Grundgesamtheit mit normalverteilten Zufallsvariablen stammt. Dieser Test ist relativ einfach, leider ist
seine Trennschärfe nicht sehr gross.
Beispiel aus dem Kapitel QQ-Plot
Man hat die folgenden Messwerte 3211.44, 4038.14, 3226.97, 1239.87, 851.5,
1769.38, 7615.08, 6865.6, 5109.29, 3221.19, 3267.5, 3930.4, 3301.19, 5270.05,
4648.16, 7804.68, 12533.99, 2240.12, 2777.09 erhalten.
Als erstes berechnen wir den Mittelwert und die Varianz der Verteilung mit
µ = 4365 und Standardabweichung zu 2782 und wählen ein Signifikanzniveau
von 95% (α = 0.05) aus. Anschliessend werden die Werte wieder aufsteigend
geordnet und anschliessend wird die Summenfunktion berechnet. Um die Summenfunktion zu berechnen nimmt man im Gegensatz zum QQ-Plot an, dass
jeder Wert das Gewicht 1/N mit N der Anzahl Messwerte besitzt. Danach wird
in einer Spalte die Differenz der Summenfunktion zu der theoretischen Funktion
(theoretische Summenfunktion der Normalverteilung mit Mittelwert µ = 4365
und Standardabweichung 2782) berechnet oder aus einer Tabelle ausgelesen.
i
851.5
1239.87
1769.38
2240.12
2777.09
3211.44
3221.19
3226.97
3267.5
3301.19
3930.4
4038.14
4648.16
5109.29
5270.05
6865.6
7615.08
7804.68
12533.99
xi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
S(xi )
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
1
19
F (xi )
0.053
0.105
0.158
0.211
0.263
0.316
0.368
0.421
0.474
0.526
0.579
0.632
0.684
0.737
0.789
0.842
0.895
0.947
1.000
|S(xi−1 ) − F (xi )|
0.103
0.131
0.175
0.223
0.284
0.339
0.341
0.341
0.347
0.351
0.438
0.453
0.541
0.606
0.628
0.816
0.879
0.892
0.998
|S(xi ) − F (xi )|
0.051
0.025
0.018
0.012
0.021
0.023
0.028
0.080
0.127
0.175
0.141
0.178
0.144
0.131
0.162
0.026
0.016
0.055
0.002
Man wählt nun den absolut grössten Wert ∆max aus der Tabelle mit den
Differenzen aus und vergleicht diesen mit einer statistischen Grösse. Falls der
Wert ∆max ist als derjenige in der Tabelle (siehe 8.4) unten kann die Hypothese,
dass die Messwerte von einer Normalverteilung kommen, auf einem Signifikanzniveau von 95% verworfen werden.
Wir haben nun 19 Messwerte und unser ∆max ist 0.178 < 0.3 und daher
kann die Nullhypothese nicht verworfen werden. Somit nehmen wir an, dass die
5.6. TEST AUF NORMALVERTEILUNG
51
Stichprobe aus einer Grundgesamtheit, welche eine Normalverteilung besitzt
entstammt.
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x, dann führt ks.test(x,”pnorm”,mean(x),sd(x))
den SK-Test durch mit Ausgabe.
Befehl
ks.test(x,”pnorm”,mean(x),sd(x))
Output
One-Sample KS-Test
data: x
D=0.178, p-Value=0.5246
alternative Hypothesis: two.sided.
Hinweise: Die Funktionen mean und sd berechnen den Mittelwert und die
Standardabweichung des Datensatz x und der p-Value¿1-0.95, daher kann
die Nullhypothese der normalverteilung der Daten nicht verworfen werden.
2. Excel
Im Moodle Kurs Hilfsmittel zur Datenanalyse kann das Excel File: 1 Stichprobe metrisch benutzt werden.
5.6.3
χ2 -Test auf Normalverteilung
Auch hier ist die Nullhypothese ist die, dass die Daten aus einer Grundgesamtheit mit normverteilten Zufallsvariablen stammt und wir betrachten auch wieder
den Datensatz aus dem Beispiel des QQ-Plots. Der Durchschnitt der Messwerte
beträgt µ = 4365 und die empirische Standardabweichung 2782. Zuerst werden
bei diesem Test die Daten in Klassen aufgeteilt. In der folgenden Tabelle sind
die Klassen und die entsprechende Anzahl der Messwerte, die in diese Klasse
gehören, eingetragen. Es muss beachtet werden, dass man die Tabelle so ergänzt,
dass die Wahrscheinlichkeit 1 ergibt. Man hat da einfach nichts gefunden.
52
KAPITEL 5. STATISTISCHE TESTS
10
Gauss
Anzahl Werte
8
6
4
2
0
0
2000
4000
6000
8000
10000
12000
14000
Anzahl Zellen
Abbildung 5.6: χ2 -Test auf Normalverteilung)
untere Grenze obere Grenze Anzahl n aus Gauss χ2
-∞
0
0
1.11
1.11
0
2000
3
2.65
0.139
2000
4000
8
4.75
0.091
4000
6000
4
5.20
0.25
6000
8000
3
3.47
0.0046
8000
10000
0
1.41
0.22
10000
12000
0
0.35
0.457
12000
14000
1
0.052
0.69
14000
∞
0
0.005
0.005
Summe
19
19
22.6
Diese benutzt man um die theoretische Anzahl nth , die in den verschiedenen
Klassen liegen sollten, zu berechnen. Mittels dieser theoretischen Anzahl kann
man anschliessend den χ2 -Test durchführen. Um den Wert zu berechnen wird
P (nexp,k −nth,k )2
berechnet.
dabei die Summe χ2 =
nth,k
Nun sollte diese Zahl der χ2 -Verteilung mit m − 3 = 9 − 3 = 6 Freiheitsgraden gehorchen. Man hat hier die Statistik, nämlich die Gaussverteilung gewählt,
welche durch den Mittelwert und die empirische Varianz eindeutig definiert ist.
Daher hat man n − 3 Freiheitsgrade (1 FG für die Statistik und je 1 FG für den
Mittelwert und die empirische Varianz)
In unserem Fall ergibt sich für 95% (siehe 8.3) ein χ2 von 12.59, dies besagt, dass
die NH (die Daten stammen aus einer Grundgesamtheit mit Gaussverteilung)
auf dem Signifikanzniveau 95% verworfen werden kann.
5.6. TEST AUF NORMALVERTEILUNG
53
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x, dann führt chisq.test(x) einen Test durch, dass
ist aber nicht derjenige den wir wollen!! Er basiert auf gleicher Wahrscheinlichkeit für jede Klasse. Wir müssen also zuerst die Wahrscheinlichkeiten
berechnen.
Folgendes Programm sollte funktionieren.
Daten in x.
Befehle
histo=hist(x)
probs=pnorm(histo$breaks,mean(x),sd(x))
proba=c()
for(i in 2:(length(probs)))
delta=probs[i]-probs[i-1]
proba=c(proba,delta)
delta=1-sum(proba)
proba=c(proba,delta)
coun=c(0,histo$counts,0)
a=chisq.test(coun,p=proba)
Befehl für Ausgabe p-Wert
1-pchisq(a$statistics,df=length(proba)-3)
Hinweis: Die Funktionen mean und sd berechnen den Mittelwert und die
Standardabweichung des Datensatz x.
54
KAPITEL 5. STATISTISCHE TESTS
5.6.4
t-Test
Ein-Stichproben Test
Man untersucht hier mittels einer Stichprobe die Frage, ob eine Grundgesamtheit einen bestimmten Mittelwert überschreitet oder nicht. Die Voraussetzung
ist, dass die Daten normalverteilt sind. Sind die Daten nicht normalverteilt, so
muss man den Wilcoxon-Test verwenden, welcher aber Mediane vergleicht.
Beispiel
Der Gehalt eines Wirkstoffs einer Tablette sollte innerhalb gewisser Grenzen
liegen. Ist der Gehalt zu hoch, so kann dies gesundheitsschädlich sein, ist er
dagegen zu tief, so ist die Tablette nicht mehr wirksam.
Die Entscheidung kann anhand der Tabelle getroffen werden (µ0 ist der Mittelwert der Grundgesamtheit):
Hypothese
einseitiger Test
H0 : µ 1 ≥ µ 0
H1 : µ 1 < µ 0
zweiseitiger Test
H0 : µ 1 = µ 0
H1 : µ1 6= µ0
√0
Testgrösse
t = (sx−µ
x / n)
Rückweisung H0 ablehnen falls t < −tα,n−1 H0 ablehnen falls |t| > tα/2,n−1
Beispiel
Man habe bei 5 Tablette den Wirkstoff (Sollwert=100mg) gemessen und erhält
x̄ = 95.5 mg und eine empirische Varianz von sx = 4 mg2 .
1. Kann auf einem Signifikanzniveau von 95% gesagt werden, dass der Gehalt der Tablette grösser als 100mg ist?
Man erhält t =
95.5−100
4
√
5
= −2.52. Aus einer Tabelle erhält man t0.05,5−1 =
2.132, daraus ergibt sich, dass die NH x̄ ≥ 100mg abgelehnt werden muss
(einseitiger Test).
2. Kann man mit auf einem Signifikanzniveauvon 95% sagen, dass der Gehalt
der Tablette gleich 100mg ist?
Man erhält wie oben t = 2.52 und daraus 2.52 < t0.05/2,5−1 = 2.776 (siehe
8.2). Man kann also die NH, dass der Mittelwert 100mg beträgt, nicht
verwerfen.
5.6. TEST AUF NORMALVERTEILUNG
55
3000
2000
1000
Sample Quantiles
4000
Normal Q−Q Plot
−2
−1
0
1
2
Theoretical Quantiles
Abbildung 5.7: QQ-Plot Datensatz 2
Beispiel 2
Beim Beispiel aus dem QQ-Plot Kapitel sind die Daten nicht normalverteilt, daher kann der t-Test nicht angewandt werden. Ich habe aber noch
einen anderen Datensatz der Anzahl aktiver Zellen der Biotechnologen erhalten. Sie haben die Daten 543, 944, 1227, 1428, 1622, 1649, 1727, 1774,
2188, 2356, 2402, 2517, 2529, 2771, 2809, 2892, 2906, 3076, 4485 erhalten.
Im QQ-Plot (Abbildung 5.7) ist ersichtlich, dass diese schon eher normalverteilt sind.
Die Daten sind nach dem KS-Test (p-Wert=0.94) und dem χ2 Test (pWert=0.62) normalverteilt. Der Mittelwert beträgt x = 2202 und die Standardabweichung sx = 908.
Wir können uns nun fragen, ob die Zellaktivität bei einem Signifikanzniveau von 98% 2000 beträgt. Dazu berechnen wir den t-Wert:
t=
|2202−2000|
908
√
19
= 0.97115
Aus der Tabelle (siehe 8.2) liest man ein kritischen t-Wert von t0.02/2,19−1 =
2.552, daher kann die Nullhypothese nicht verworfen werden.
56
KAPITEL 5. STATISTISCHE TESTS
Hilfsmittel
(a) Statistikprogramm R
Daten seien im Vektor x, dann führt t.test(x,alternative =”two.sided”resp.
”less”resp. ”greater”, mu =) den t-Test durch.
Für das obiges Beispiel.
Befehl
t.test(x,mu=2000,alternative=two.sided”)
Output
One-Sample t-Test
data: x
t=0.97, df=18, p-value=0.34
alternative Hypothesis: true mean is not equal to 2000
95% condidence interval:
1764 2640
Der p-Wert ist grösser als 0.02/2, daher kann die NH nicht abgelehnt
werden.
(b) Excel
Im Moodle Kurs Hilfsmittel zur Datenanalyse kann das Excel File: 1
Stichprobe metrisch benutzt werden.
Zwei-Stichproben Test
Die Nullhypothese dieses t-Tests lautet, dass 2 Stichproben aus der selben
Grundgesamtheit mit demselben Erwartungswert stammen. Die Prüfgrösse wird
aus der Anzahl der Daten, dem Mittelwert und der Standardabweichung der beiden Messreihen gebildet. Sie gehorcht der Student-t-Verteilung.
Die Idee hinter dem Test ist sehr einfach. Man betrachtet die beiden berechneten Mittelwerte und schaut, wieviele Standardabweichungen sie voneinander entfernt sind. Die Standardabweichung ist dabei gegeben durch s2t =
(n1 −1)s21 +(n2 −1)s22
. Falls die Standardabweichungen stark verschieden sind, muss
n1 +n2 −2
s2
s2
der Welch-Test verwendet werden. Dabei wird s2t durch n11 + n22 berechnet. Um
zu bestimmen ob die Varianzen gleich sind kann der Levene Test benutzt werden.
5.6. TEST AUF NORMALVERTEILUNG
Hypothese
Testgrösse
Rückweisung
57
zweiseitiger Test
H0 : µ 1 − µ 0 = ω
H1 :q
µ1 − µ0 6= ω
n2 x1 −x2 −ω
t = (nn11+n
st
2)
H0 ablehnen falls |t| > tα/2,n1 +n2 −2
Beispiel
Man habe bei einer Charge bei 5 Tablette den Wirkstoff gemessen und man
erhält x̄1 = 96 mg und eine empirische Varianz von s1 = 4.6 mg2 und bei einer
2. Charge einen Mittelwert von x̄1 = 95.1 mg und eine empirische Varianz von
s1 = 3.5 mg2 . Die Varianzen seien gleich (Levene-Test p-Wert=0.686).
Kann auf einem Signifikanzniveau von 95% gesagt werden, dass der Gehalt
in den Tabletten in den beiden Chargen gleich sind?
q
5·7 (96−95.1)
√
= 0.367. Aus einer Tabelle
Man erhält s2t = 15.88 und t = (5+7)
15.88
(siehe 8.2) erhält man t0.025,5+7−2 = 2.228, daraus ergibt sich, dass die NH, dass
beide Mittelwerte identisch sind nicht abgelehnt werden kann.
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x1 und x2, dann führt t.test(x1,x2,var.equal=TRUE)
den t-Test durch. Aufpassen standardmässig ist der Welchtest eingestellt.
Für das obiges Beispiel.
Befehl
t.test(x1,x2,var.equal=TRUE)
Output
Two-Sample t-Test
data: x1 and x2
t=0.37, df=10, p-value=0.72
alternative Hypothesis: true differences in means is not equal to 0
Der p-Wert ist grösser als 0.025, daher kann die NH nicht abgelehnt werden.
2. Excel
Im Moodle Kurs Hilfsmittel zur Datenanalyse kann das Excel File: 2 Stichproben metrisch benutzt werden.
58
KAPITEL 5. STATISTISCHE TESTS
Bemerkungen
1. Sind die Daten nicht normalverteilt, so sollte der Mann Whitney U-Test
verwendet werden.
2. Besitzt man mehr als 2 Stichproben die man miteinander vergleichen
möchte so sollte bei normalverteilten Daten ANOVA und sonst KruskalWallis verwendet werden.
5.6.5
Grubbs Test
Beim Ausreissertest nach Grubbs wird getestet ob eine Stichprobe einen Ausreisser enthält. Die Voraussetzung für den Grubbstest ist, dass die Stichprobe
normalverteilt ist. Wir haben gesehen, dass man dies mittels eines QQ-Plots
oder einem χ2 -Test herausfinden kann. Sind die Daten nun normalverteilt, so
standardisiert man diese zuerst. Anschliessend betrachtet man nur den Wert der
vom Betrage her die grösste Abweichung vom Mittelwert besitzt und schaut in
der Tabelle am Ende nach, ob dieser Wert grösser als der Tabellenwert ist. Ist
er grösser so wird er als Ausreisser betrachtet und aus der Stichprobe entfernt.
Diese Prozedur darf man auch mehrmals Anwenden.
Beispiel
Beim Beispiel für den Volumenaufbau von Mundgewebe (t-Test)
merkt, dass die Daten normalverteilt sind. Besitzen wir da bei
kanzniveau von 95% einen Ausreisser? Der grösste (4485) resp.
Wert besitzt ein zex von 2.51 resp −1.83. Aus der Tabelle (siehe
ein zkr = 2.681. Damit ist keiner der Werte ein Ausreisser.
haben wir beeinem Signifikleinste (543)
8.5) liest man
5.7. ZUSAMMENFASSUNG
59
Hilfsmittel
1. Statistikprogramm R
Daten seien im Vektor x, dann führt grubbs.test(x,two.sided=TRUE) den
Grubbs-Test durch.
Für das obiges Beispiel.
Befehl
grubbs.test(x,two.sided=TRUE)
Output
Grubbs test for one outlier
data: x
G=2.51, U=0.629, p-value=0.108
alternative Hypothesis: highest value 4485 is an outlier
Der p-Wert ist grösser als 0.05, daher kann die NH nicht abgelehnt werden.
5.7
Zusammenfassung
Ein paar Fragen
1. Was ist eine Freiheitsgrad? Worum dividiert man bei der empirischen Varianz durch n − 1?
2. Was für verschiedene Tests zur Prüfung auf Normalverteilung kennen sie?
3. Was kann man mittels χ2 -Test testen?
4. Was ist ein Konfidenzintervall?
5. Wo kann die Student t-Verteilung benutzt werden?
6. Was für verschiedene t-Tests existieren?
7. Wie kann man einen Ausreisser definieren?
8. Was für einen Ausreissertest kennen sie? Welche Bedingungen müssen
erfüllt sein?
60
KAPITEL 5. STATISTISCHE TESTS
Kapitel 6
Messfehler
Bei einer Messung können grundsätzlich zwei verschiedene Fehler das Messresultat verfälschen.
Beispiel
Wir werfen einen Stein aus dem 3. Stock und messen mit einer Stoppuhr, wie
lange der Stein braucht bis er unten auftrifft. Nun wiederholen wir das Experiment ein paar Mal und betrachten die erhaltenen Messwerte. Diese verteilen
sich gemäss der Normalverteilung um den Mittelwert. Wir sehen also, dass die
einzelnen Messungen zufällig um den Mittelwert verteilt sind. Solche Fehler werden statistische Messfehler genannt.
Nehmen wir nun an, dass unsere Uhr nicht exakt läuft, was normalerweise der
Fall ist. Läuft sie zum Beispiel zu langsam, so messen wir grundsätzlich eine zu
kurze Zeit. Ein solcher Fehler wird systematischer Fehler genannt.
Im folgenden werden wir uns nur um die Behandlung von statistischen Fehlern
kümmern.
6.1
Ein Messwert
Normalerweise wird eine Messung wiederholt und danach bestimmt man den
Mittelwert und das Vertrauensintervall.
Die Wiederholung der Messung ergibt viel mehr Information als eine einzige
Messung. Mit der Wiederholung der Messung erhält man auch eine Information
über die Unsicherheit des Mittelwertes.
Bei einer einzelnen Messung muss man sich Informationen über die Messungenauigkeit σ beschaffen. Man hat verschiedene Möglichkeiten dazu.
1. Schätzung für σ aus früheren gleichartigen Messungen.
2. Die Gerätebeschreibung enthält eine Angabe zu σ.
61
62
KAPITEL 6. MESSFEHLER
6.2
Fehlerfortpflanzung
Beispiel
Wir betrachten zur Vereinfachung eine Messung, bei welcher das Resultat nur
von einer Variable abhängig ist. Nehmen wir dazu das Experiment der Bestimmung der Federkonstanten D mittels der Schwingungsfrequenz einer Feder aus
dem Physikpraktikum
4π 2 m
.
D=
τ2
Nehmen wir nun an, dass die Masse m sehr genau gemessen werden kann
und daher dieser Fehler sicher viel kleiner ist als derjenigen der Messung der
Periodendauer τ0 = 0.5 s. Die Messung der Periodendauer sei auf ∆τ0 = 0.1 s
genau bestimmt. Um den Fehler der Federkonstante abzuschätzen, nähern wir
die Funktion D(τ ) um den Punkt τ = τ0 durch eine Gerade an. Bei mehrdimensionalen Funktionen wird die Funktion dann durch eine Ebene approximiert.
Diese Prozedur wird Linearisierung der Funktion genannt.
Die Linearisierung der Federkonstante D(τ ) um den Punkt τ = τ0 ist gegeben durch:
D(τ ) =
4π 2 m
+
τ02
−2 · 4π 2 m (τ − τ0 ) .
τ3
τ =τ0
Diese funktionelle Abhängigkeit liefert durch Einsetzen von τ = τ0 ± ∆τ0
4π 2 m −2 · 4π 2 m ±
D=
∆τ0 .
τ02
τ03
In unserem Fall ergibt dies eine Federkonstante von D = 1.58 N/m und eine
Unsicherheit von ±0.06 N/m.
Definition 6.1 (Fehlerfortpflanzung)
Nehmen wir an, dass wir eine
Funktion f (x1 , x2 . . . xn ) von mehreren Veränderlichen xi mit den Unsicherheiten ∆xi haben. Nun wird diese Funktion bezüglich allen Veränderlichen
linearisiert und anschliessend nach Pythagoras die Distanz gemessen (Annahme: Messgrössen sind unabhängig und normalverteilt). Dies ist dann genau die
absolute Unsicherheit ∆ des Messresultats.
∆2 =
∂f
∂x1 ∆x1
2
+
∂f
∂x2 ∆x2
2
+ ...+
∂f
∂xn ∆xn
2
=
n P
∂f
i=1
∂xi ∆xi
2
Spezialfälle
1. Funktion ist eine Summe:
f = x1 + x2 ⇒ ∆2 = ∆x21 + ∆x22
2. Funktion ist ein Produkt
f=
β γ
xα
1 x2 x3
∆2
... ⇒ 2 =
f
2 2 2
∆x1
∆x2
∆x3
α
+ β
+ γ
+ ...
x1
x2
x3
6.3. KORRELATION
6.3
63
Korrelation
Häufig haben wir den Fall, dass man zwei Variablen misst und untersucht, ob
diese einen Zusammenhang aufweisen; z.B. Messung der Fallzeit und Höhe eines
Falles, die Konzentration einer Lösung und Absorption von Licht.
6.3.1
Deskriptive Statistik
Es seien n Wertepaare (xi |yi ) mit quantitativen Variablen (metrische Daten)
erhoben worden. Nun stellt sich die Frage, ob ein Zusammenhang zwischen den
Grössen x und y besteht. Dazu erstellt man zuerst einmal ein Streudiagramm
und betrachtet dieses.
Es gibt statistische Kennzahlen, welche die Stärke des Zusammenhangs beschreiben. Die Pearson-Korrelation (meist kurz Korrelation genannt) misst Stärke
und Richtung des linearen Zusammenhangs.
Definition 6.2 (Pearson-Korrelation) Seien x resp. y die Mittelwerte der
sx resp. sy die empirischen Standardabweichungen der Variablen x resp. y, dann
berechnet sich der Pearson Korrelationskoeffizient folgendermassen.
(x1 − x) (y1 − y) (x2 − x) (y2 − y)
(xn − x) (yn − y)
1
+
+ ...+
r=
n−1
sx
sy
sx
sy
sx
sy
Man sieht, dass die Funktion symmetrisch in x resp. y ist.
Eigenschaften des Pearson Korrelationskoeffizienten
• +1, wenn alle Punkte exakt auf einer Geraden mit positiver Steigung
liegen.
• −1, , wenn alle Punkte exakt auf einer Geraden mit negativer Steigung
liegen.
• nahe bei -1 oder +1, wenn die Punkte eng um eine Gerade streuen.
• 0, wenn kein linearer Zusammenhang zwischen x und y besteht.
Wichtig: Ein Korrelationskoeffizient soll nie ohne Betrachtung des dazugehörigen Streudiagramms betrachtet werden. Falls der Zusammenhang nicht linear
ist kann auch der Rangkorrelationskoeffizient nach Spearman benutzt werden.
64
KAPITEL 6. MESSFEHLER
6.4
Regression
Falls die Punkte im Streudiagramm ’schön’ auf einer Linie liegen, so kann man
versuchen, den Zusammenhang durch eine Funktion zu beschreiben. Dies macht
vor allem dann Sinn, falls die Funktion aus theoretischen Überlegungen bekannt ist. Dann versucht man durch anpassen der Parameter die Daten so gut
wie möglich durch die Funktion zu beschreiben. Diese Suche nach den Parametern wird Regression genannt. Ist die Funktion linear in den Parametern, dann
kann die Methode aus dem Analysis-Skript benutzt werden. Häufig kann man
aber die Werte auch so transformieren, dass man auf einen linearen Zusammenhang kommt.
Beispiel
Im Praktikum haben wir den Wasserstand in einem Gefäss mit Ausfluss in
Abhängigkeit der Zeit gemessen. Dieser Ausfluss sollte gemäss Theorie den folgenden Zusammenhang besitzen:
2
V (t) = (A − B t) .
Sind mehr Messpunkte (ti , Vi ) als Parameter vorhanden so ist das Gleichungssystem überbestimmt und man muss definieren, was beste Approximation heisst.
Die obige Gleichung können wir umformen und erhalten
V (t) − (A − B t)2 = 0 .
Diese Relation sollte für alle Wertepaare exakt stimmen, falls die Messungen
exakt und das Modell exakt die Abhängigkeit der beiden Messwerte voneinander angibt. Dies ist aber nie der Fall!!!
Wir definieren zuerst das Residuum ri = Vi − V (ti ).
Anmerkungen
Im folgenden werden wir die Regression für Funktionen behandeln, bei welchen wir alles analytisch berechnen können. Es tauchen aber auch in der Chemie
häufig Fälle auf, welche anders behandelt werden müssen. Im folgenden zähle
ich ein paar Beispiele auf.
1. Funktionen welche nicht-linear in den Koeffizienten sind
2. verschiedene Unsicherheiten für verschiedene x−Werte
3. Berücksichtigung, dass x und y Werte Unsicherheiten aufweisen.
Benutzt für solche Fälle doch die Möglichkeit, dass ihr Anspruch auf Statistikberatung an unserem Institut habt.
6.4. REGRESSION
6.4.1
65
Methode der kleinsten Quadrate
Um diese Methode anwenden zu können sollten alle Messfehler der Vi in etwa gleich gross und diejenige der ti viel kleiner als diejenigen der Vi sein. Im
Praktikum
haben wir die Messwerte die beste Approximation an die Funktion
√
V = A − Bt gesucht. In diesem Fall sind dann ein paar der obigen Annahmen
nicht mehr genau erfüllt. Aber häufig ist eine solche Approximation genügend.
Die beste Approximation wird dann erreicht, falls die Summe aller Residuen
n
P
rj2 minimal ist.
j=1
Wie gut die Daten approximiert werden, wird durch das Bestimmtheitsmass R2 (0 ≤ R2 ≤ 1) angezeigt. Wie im Analysis Skript besprochen sollte nie
nur das Bestimmtheitsmass zur Kontrolle der Approximation betrachtet werden.
Definition 6.3 (Bestimmtheitsmass) Sei ri das Residuum und y der Mittelwert aller yi , dann wird das Bestimmtheitsmass folgendermassen berechnet.
R2 = 1 − P
n
j=1
n
P
j=1
rj2
(yj − y)2
Grafische Darstellung
Die Daten sollten in einem Plot als Punkte und die Regressionskurve als Linie
dargestellt werden.
Lineare Regression in Koeffizienten
Ein Spezialfall der Regression ist die Anpassung an eine Gerade, welche nicht
zwingendermassen durch den Nullpunkt geht (in den meisten praktischen Fällen
ist der Nullpunkt nicht absolut sicher, sondern das Resultat einer Justierung).
In Analysis haben wir gesehen wir man die Regression mit Hilfe von Matrizen
berechnet. Hier geben wir einmal die Resultate mit Hilfe von Summen an.
Gleichung:
y(x) = ãx + b̃
Steigung:
ã =
n
P
(xi yi − x̄ · y)
i=1
n
P
i=1
Achsenabschnitt:
(x2i − x̄2 )
b̃ = ȳ − ãx̄
Aus der Berechnung des Achsenabschnitts sieht man, dass die Summe der
n
P
ri = 0 ist (speziell). Die 2. spezielle Eigenschaft ist, dass das BeResiduen
i=1
stimmtheitsmass exakt gleich dem Pearson- Korrelation Koeffizient ist: R2 = r2 .
66
KAPITEL 6. MESSFEHLER
Es gibt 2 grundsätzlich verschiedene Arten die Regression zu benutzen.
1. Wir haben ein lineares Gesetz und bestimmen Konstanten eines Systems
(z.B. Bestimmung der Federkonstante)
2. Kalibrationsgerade
Die Unsicherheiten der Koeffizienten ã und b̃ kann mit Hilfe der Messwerte
berechnet werden. In Analysis haben wir gesehen, dass man die Suche nach
der besten Gerade auf ein überbestimmtes lineares System von Gleichungen
kommt, welches durch Ax = B gegeben ist. Die Lösung ergibt sich dann durch
Berechnung von x = (AT A)−1 AT B. Die Unsicherheit der Koeffizienten sind
dann durch die Diagonalelemente der folgenden Matrix gegeben.
∆x2 =
−1
rT r
AT A
(n − 2)


1 x1
 1 x2 



Dabei ist r der Residuenvektor (ri = yi −(ãxi +b̃)) und A = 
 1 x3 . Dann
 ···

1 xn
ist die Unsicherheit ∆b̃ von b̃ gleich der Wurzel des ersten Diagonalelementes der
Matrix ∆x2 und diejenige von ã ist die Wurzel des zweiten Diagonalelementes
∆ã. Um die Vertrauensintervalle der Koeffizienten oder der Kalibriergeraden zu
berechnen geht man davon aus, dass die Residuen normalverteilt sind. Dies sollte
man üblicherweise noch testen (siehe Kapitel Hypothesentests). Sind die Residuen normalverteilt, dann gilt, dass kann man um die Vertrauensintervalle zu
erhalten die Unsicherheit mit dem entsprechenden t-Wert (zweiseitig) multiplizieren. Die Vertrauensintervalle der Parameter sind dann durch ã±t1−α/2,n−2 ∆ã
und b̃ ± t1−α,/2n−2 ∆b̃ gegeben.
Man kann auch einen t-Test mithilfe dieser Infos durchführen (genaueres
siehe folgendes Beispiel).
Mit Hilfe all dieser Informationen kann ein α Prozent Intervall für den berechneten Funktionswert an der Stelle x0 angegeben werden. Wird dies für viele
Punkte x0 berechnet und anschliessend im Graphen eingetragen, so erhält man
die Fehlertrompeten.


n
2
P
(x0 −x) 
1
rj2 .
mit s2 = n−2
Man berechnet zuerst g(x0 ) = s2  n1 + P
n
(xi −x)2
i=1
Anschliessend sind die beiden Fehlertrompeten gegeben durch
p
ã · x0 + b̃ ± t1−α/2,n−2 g(x0 )
.
j=1
6.4. REGRESSION
67
Beispiel 1
Wir haben im Physikpraktikum die Federkonstante durch anhängen von verschiedenen Gewichten an die Feder bestimmt.
Gewicht F [N] Auslenkung x [m]
2
0.019
4
0.04
6
0.06
7
0.071
Da man einen linearen Zusammenhang (mit Achsenabschnitt) erwartet (F =
D · x − D · x0 , D Federkonstante und x0 Gleichgewichtslage). Schreiben wir einmal die Gleichungen mit Steigung ã und Achsenabschnitt b̃ hin.
2 = ã · 0.019 + b̃
4 = ã · 0.04 + b̃
6 = ã · 0.06 + b̃
7 = ã · 0.071 + b̃
Dieses Gleichungssystem kann man nun mithilfe von Matrizen schreiben.

 

2
0.019 1
 4 
 0.04 1 
ã




.
, B =   und x =
Ax = B mit A = 
6
0.06 1 
b̃
7
0.071 1
Man macht die folgenden Matrixmultiplikationen und erhält:
0.010602 0.19
AT A =
0.19
4
634.1 −30.12
(AT A)−1 =
−30.12 1.6807
1.055
AT B =
19
96.7
T
−1 T
Damit berechnet man die Koeffizienten zu x = (A A) A B =
0.16
Ein auslesen aus der Lösung ergibt, dass F = 96.7x + 0.16 ist. Durch Koeffizientenvergleich erhält man ã = D = 96.7 und b̃ = D · x0 = 0.16. Da es sich
um eine Messung mit einer gewissen Unsicherheit handelt, können wir nun das
95% Vertrauensintervall der beiden Koeffizienten bestimmen.
Dazu müssen wir zuerst die Residuen berechnen.


−0.00602
 0.02473 

r = Ax − B = 
 −0.041218 
0.02251
Die Residuen müssten nun auf Normalverteilung getestet werden, bei 4 Werten macht das aber wenig Sinn, daher lassen wir das nun weg und berechnen
direkt die geschätzten Varianzen der Faktoren.
68
KAPITEL 6. MESSFEHLER
∆x2 =
rT r
(n−2)
−1
AT A
=
0.905 −0.043
−0.043 0.00240
Damit erhält man also die folgenden Vertrauensintervalle (95%):
√
ã: 96.7 ± tα/2,4−2 0.905 = 96.7 ± 4.1
√
b̃: 0.16 ± tα/2,4−2 0.00240 = 0.16 ± 0.21
Wir können nun auch einen t-Test durchführen (Annahme Residuen sind
normalverteilt) und uns Fragen ob die Federkonstante 100N/m und die Gleichgewichtslage x0 gleich 0 ist.
Bei der Federkonstanten können wir direkt den t-Test (siehe 8.2 t-Wert
(FG=4-2)= 4.3) anwenden. (Hinweis: der Wurzelfaktor wurde nicht vergessen!)
t=
|100−96.7|
√
0.905
= 3.47
Damit kann die NH, dass die Federkonstante 100N/m beträgt nicht verworfen werden.
Um zu testen, ob die Gleichgewichtslage 0 ist, müssen wir zuerst die Gleichgewichtslage berechnen. Man erhält durch Koeffizientenvergleich b̃ = −D · x0 ,
also x0 = −Db̃ = −0.0016. Die Unsicherheit dieses Wertes müssen wir mithilfe
der Fehlerfortpflanzung (partiellen Ableitungen) berechnen.
r
∆x0 =
1
· ∆b̃
−D
2
+
b̃
D2 ∆D
2
= 5 · 10−4
Damit kann man nun den t-Wert für die Hypothese x0 = 0 berechnen.
t=
|0−(−0.0016)|
5·10−4
= 3.19
Man erhält also, dass die NH nicht verworfen werden.
Zum Abschluss wollen wir noch die Fehlertrompeten zeichnen. Das s2 ist
n
P
(xi − x)2 = 0.001577 und damit
= 0.00143, x̄ = 0.0475 und
gleich 0.00265
4−2
i=1
−0.0475)2
. In der Abbildung 6.1 sind die
erhält man g(x0 ) = 0.00143 41 + (x00.001577
Messwerte, die Approximation und die Fehlertrompeten abgebildet.
Man bemerkt nun, dass die Kurve viel zu genau ist. Von Auge sind die 3 Kurven praktisch identisch. Um bei solchen Fällen doch etwas aussagen zu können
trägt man die Residuen auf. Zusätzlich sieht man beim Auftragen der Residuen, ob ein Trend in den Residuen steckt. Dies würde darauf hindeuten, dass die
Daten durch durch eine andere Abhängigkeit zusammen verknüpft sind, da die
Messpunkte statistisch um den Wert 0 verteilt sein müssen. In der Abbildung
6.2 sind die Residuen und die Fehlertrompeten aufgetragen.
6.4. REGRESSION
69
12
Data
Regresssion
10
Vertrauensband
F[N℄
8
6
4
2
0
-2
0
0.02
0.04
0.06
0.08
0.1
x[m℄
Abbildung 6.1: In dieser Abbildung sind die Messwerte der Bestimmung der
Federkonstanten, die Approximation und die Fehlertrompeten eingezeichnet.
0.25
Data
Regresssion
0.2
Vertrauensband
0.15
Residuum
0.1
0.05
0
-0.05
-0.1
-0.15
-0.2
-0.25
0
0.02
0.04
0.06
0.08
0.1
x[m℄
Abbildung 6.2: In dieser Abbildung sind Residuen der Bestimmung der Federkonstanten und die Fehlertrompeten eingezeichnet.
70
KAPITEL 6. MESSFEHLER
Hilfsmittel
1. Statistikprogramm R
Daten seien in den Vektoren x und y, dann führt lm(y x) eine lineare Regression durch.
Für das obiges Beispiel.
Befehl
a=lm(y x)
in a ist alles gespeichert.
summary(a)
Output
lm(formula=y x)
1
2
3
4
Coefficients:
−0.00602 0.02473 −0.041218 0.02251
Estimate StdError tvalue
P r(> |t|)
(Intercept)
0.156
0.049 3.198
0.0854 Multiple Rx
96.7
0.95
102 9 · 10−5 ∗ ∗∗
Squared: 0.9998, adjusted R-Squared 0.9997
Residuals:
Beispiel 2
Wir haben im Physikpraktikum den zeitlichen Verlauf des Ausflusses einer
Flüssigkeit aus einem zylinderförmigen Gefäss betrachtet. Wir haben gesehen,
dass die zeitliche Abhängigkeit der Füllhöhe im Gefäss dem Gesetz h(t) =
at2 + bt + c gehorcht. Im folgenden gebe ich die Daten nicht an und gebe ein
paar Grafiken und ein paar p-Werte an.
Der lineare Fit ist in der Abbildung 6.3 ersichtlich. Man sieht direkt, dass
eine lineare Funktion die Daten schlecht beschreibt.
Ein χ2 Test auf normalverteilung der Residuen ergibt einen p-Wert von 0.57.
Die Residuen sind also normalverteilt. Hier sieht man, dass ein normalverteilungstest für die Residuen nicht reicht. Man kann auch die Korrelation der
Residuen testen . In diesem Fall zeigt sich, dass die Residuen stark korrelliert
sind.
Macht man nun einen quadratische Fit, so erhält man die Abbildungen 6.4.
Man sieht direkt, dass die Funktion viel besser ist.
6.4. REGRESSION
71
Residuen linearer Fit
0.01
Residuen
−0.01
0.05
0.00
0.10
Hoehe [m]
0.15
0.02
0.20
0.03
linearer Fit
0
20
40
60
80
100
120
140
0
20
40
60
Zeit[s]
80
100
120
140
Zeit[s]
Abbildung 6.3: In der Abbildung links sind die Messwerte und der lineare Fit
abgebildet. Im rechten Teil habe ich die Residuen geplottet.
Residuen quadratischer Fit
5e−04
0e+00
Residuen
0.15
0
20
40
60
80
Zeit[s]
100
120
140
−1e−03
0.05
−5e−04
0.10
Hoehe [m]
0.20
quadratischer Fit
0
20
40
60
80
100
120
140
Zeit[s]
Abbildung 6.4: In der Abbildung links sind die Messwerte und der quadratische
Fit mit den Konfidenzintervallen abgebildet. Die Konfidenzintervalle sind nicht
sichtbar, da sie genau auf der Kurve liegen. Im rechten Teil habe ich die Residuen
mit den Konfidenzintervallen geplottet.
72
KAPITEL 6. MESSFEHLER
Ein χ2 Test auf normalverteilung der Residuen ergibt einen p-Wert von 0.53.
Die Residuen sind also normalverteilt. In diesem Fall zeigt sich, dass die Residuen noch leicht korreliert sind.
6.5
Zusammenfassung
Bei Messungen ergeben sich häufig Daten, welche einen Zusammenhang besitzen. Mittels der Methode der Regression können die Parameter der Kurve
bestimmt werden, welche die beste Approximation ergibt. Es sollte aber üblicherweise der funktionale Zusammenhang zwischen den beiden Grössen bekannt
sein.
Mittels Residuen muss das Resultat der Regression überprüft werden. Einerseits durch die Berechnung des Bestimmtheitsmasses und andererseits grafisch.
Kapitel 7
Boltzmann Verteilung
Die Boltzmannverteilung beschreibt die Besetzungsverteilung eines physikalischen Systems im thermischen Gleichgewicht.
7.1
Diskrete Boltzmann Verteilung
Gegeben sei ein quantenmechanisches System mit n möglichen diskreten Energiezuständen Ek mit der Temperatur T . Dann ist die Wahrscheinlichkeit pk , es
im Zustand mit der Energie Ek zu finden gegeben durch:
Pk =
−
gk e
Pn
j=1
gj
Ek
kB T
Ej
−
e kB T
Dabei ist gk die Anzahl der entarteten Energiezuständen mit der Energie Ek ,
k die Boltzmannkonstante kB = NRa = 1.38 · 10−23 J/K (Na ist die Avogadrokonstante). Wie ihr vielleicht schon gehört habt entspricht kB T der thermischen
Energie.
Die innere Energie pro Mol ist dann durch den Erwartungswert der Energie
gegeben.
U = Na E(E) = Na
n
P
pk Ek
k=1
Die spezifische Molwärme wird dann durch die Ableitung der inneren Energie nach der Zeit gegeben.
7.1.1
spezifische Molwärme
Wir betrachten ein System mit 2 Energiezuständen, welche nicht entartet sind.
Nehmen wir dabei an, dass E1 = 0 und E2 = E ist. Da der Energienullpunkt
völlig willkürlich ist, kann man immer dies bei den statistischen Betrachtungen
immer machen. Dann ist die Summe der Exponentialfunktionen gegeben durch:
− E
− E
e0 + e kB T = 1 + e kB T , somit ergeben sich die Wahrscheinlichkeiten
73
74
KAPITEL 7. BOLTZMANN VERTEILUNG
1
6
p1
p2
5
4
0.6
cv
Besetzungszahl
0.8
3
0.4
2
0.2
1
0
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0
2
4
6
8
10
T
Temperatur
Abbildung 7.1: Links sind die Wahrscheinlichkeiten der beiden Zustände aufgetragen in Abhängigkeit der Temperatur aufgetragen. Rechts wird die Abhängigkeit der molaren Wärmekapazität eines Systems mit 2 Zuständen von der Temperatur gezeigt.
p1 =
1
− E
1+e kB T
und p2 =
E
kB T
− E
1+e kB T
−
e
Man erhält damit eine innere
U = Na (p1 E1 + p2 E2 ) =
Energie von
− E
− E
1
e kB T
e kB T
Na 0 − E + E
= Na E
.
− E
− E
1+e
kB T
kB T
1+e
1+e
kB T
Die spezifische Molwärme ist dann gegeben durch:
cv =
7.2
E
−
N ·E 2
2 e kB T
a
− E
k
T
2
B
kB T
1+e
kontinuierliche Boltzmann Verteilung
Man kann eigentlich die diskrete Boltzmann Verteilung benutzen und die Summen durch Integrale ersetzen. Man muss sich dazu noch bewusst sein, dass es
sich am eine kontinuierliche Verteilung handelt. Die Wahrscheinlichkeitsdichte
für ein Teilchen mit der Energie E ist gegeben durch
−
g(E)e
p(E) =
R
E
kB T
−
g(E)e
E
kB T
dE
ganze E
g(E) ist die Zustandsdichte der Energie E.
7.2.1
Maxwell-Boltzmann Verteilung
Man sucht die Wahrscheinlichkeit, dass ein Teilchen mit der Masse m in einem idealen Gas eine gewisse Geschwindigkeit v besitzt. Die Energie ist dann
natürlich durch die kinetische Energie des Teilchens gegeben (E = 21 mv 2 ). Diese
ist immer grösser gleich 0. Daher sind die Integrationsgrenzen gegeben durch
E = 0 und E = ∞. Nun stellt sich noch die Frage, wie gross g(E) ist. Die
Anzahl der ’Zustände’ ist proportional zu der Fläche der Kugel mit Radius v,
7.3. ZUSAMMENFASSUNG
75
0.0035
T = 100K
T = 300
T = 2000K
0.003
0.0025
p(v)
0.002
0.0015
0.001
0.0005
0
0
500
1000
1500
2000
v[m/s]
Abbildung 7.2: Die Geschwindigkeitsverteilung p(v) vom Gas N2 bei den angegebenen Temperaturen.
also zu 4πv 2 .
Achtung: Hier ist m die reale Masse des Teilchens nicht die Molmasse.
−
g(E)e
p(E) =
E
kB T
−
R
g(E)e
E
kB T
=
dE
ganze E
2
− mv
2kB T
2
∞
R
− mv
4πv 2 e 2kB T
4πv 2 e
Wir haben gesehen, dass
R∞
4πv 2 e
0
2
mv
− 2k
T
B
Wahrscheinlichkeitsdichte gegeben durch:
q 2
π
7.3
m
kB T
32
dv
0
dv =
2πkB T
m
23
ist. Daher ist die
2
e
mv
− 2k
T
B
Zusammenfassung
Die Wahrscheinlichkeit ein physikalisches System mit der Energie E bei der
− E
Temperatur T diesem Zustand zu finden ist proportional zu e kB T . In der
Quantenmechanik gibt es dann noch gewisse Einschränkungen, auf welche wir
hier nicht eingehen.
76
KAPITEL 7. BOLTZMANN VERTEILUNG
Kapitel 8
Tabellen
8.1
Normalverteilung
Werte der Verteilungsfunktion der Standardnormalverteilung für typische Werte
von z.
0.0000 0.0100 0.0200 0.0300 0.0400 0.0500 0.0600 0.0700
z
0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279
0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675
0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064
0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443
0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808
0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157
0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486
0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794
0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078
0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340
1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577
1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790
1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980
1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147
1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292
1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418
1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525
1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616
1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693
1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756
2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808
2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850
2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884
2.3 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911
2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932
2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949
2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962
2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972
2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979
2.9 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985
77
0.0800
0.5319
0.5714
0.6103
0.6480
0.6844
0.7190
0.7517
0.7823
0.8106
0.8365
0.8599
0.8810
0.8997
0.9162
0.9306
0.9429
0.9535
0.9625
0.9699
0.9761
0.9812
0.9854
0.9887
0.9913
0.9934
0.9951
0.9963
0.9973
0.9980
0.9986
0.0900
0.5359
0.5753
0.6141
0.6517
0.6879
0.7224
0.7549
0.7852
0.8133
0.8389
0.8621
0.8830
0.9015
0.9177
0.9319
0.9441
0.9545
0.9633
0.9706
0.9767
0.9817
0.9857
0.9890
0.9916
0.9936
0.9952
0.9964
0.9974
0.9981
0.9986
78
8.2
KAPITEL 8. TABELLEN
Student t Tabelle
Tabelle der Quantile der Student’schen t-Verteilung. Die Zeilen geben bei festem Wert des Freiheitsgrades für typische Werte von q.
P (x < t)
FG
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0.600
t0.4
0.325
0.289
0.277
0.271
0.267
0.265
0.263
0.262
0.261
0.260
0.260
0.259
0.259
0.258
0.258
0.258
0.257
0.257
0.257
0.257
0.257
0.256
0.256
0.256
0.256
0.256
0.256
0.256
0.256
0.256
0.750
t0.25
1.000
0.816
0.765
0.741
0.727
0.718
0.711
0.706
0.703
0.700
0.697
0.695
0.694
0.692
0.691
0.690
0.689
0.688
0.688
0.687
0.686
0.686
0.685
0.685
0.684
0.684
0.684
0.683
0.683
0.683
0.900
t0.1
3.078
1.886
1.638
1.533
1.476
1.440
1.415
1.397
1.383
1.372
1.363
1.356
1.350
1.345
1.341
1.337
1.333
1.330
1.328
1.325
1.323
1.321
1.319
1.318
1.316
1.315
1.314
1.313
1.311
1.310
0.950
t0.05
6.314
2.920
2.353
2.132
2.015
1.943
1.895
1.860
1.833
1.812
1.796
1.782
1.771
1.761
1.753
1.746
1.740
1.734
1.729
1.725
1.721
1.717
1.714
1.711
1.708
1.706
1.703
1.701
1.699
1.697
0.975
t0.025
12.706
4.303
3.182
2.776
2.571
2.447
2.365
2.306
2.262
2.228
2.201
2.179
2.160
2.145
2.131
2.120
2.110
2.101
2.093
2.086
2.080
2.074
2.069
2.064
2.060
2.056
2.052
2.048
2.045
2.042
0.990
t0.001
31.821
6.965
4.541
3.747
3.365
3.143
2.998
2.896
2.821
2.764
2.718
2.681
2.650
2.624
2.602
2.583
2.567
2.552
2.539
2.528
2.518
2.508
2.500
2.492
2.485
2.479
2.473
2.467
2.462
2.457
0.995
t0.0005
63.657
9.925
5.841
4.604
4.032
3.707
3.499
3.355
3.250
3.169
3.106
3.055
3.012
2.977
2.947
2.921
2.898
2.878
2.861
2.845
2.831
2.819
2.807
2.797
2.787
2.779
2.771
2.763
2.756
2.750
8.3. χ2 − T ABELLE
8.3
79
χ2 − T abelle
Tabelle der Quantile der χ2 -Verteilung. Die Zeilen geben bei festem Wert des
Freiheitsgrades für typische Werte von q.
P (x < t)
FG
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0.600
χ20.4
0.708
1.833
2.946
4.045
5.132
6.211
7.283
8.351
9.414
10.473
11.530
12.584
13.636
14.685
15.733
16.780
17.824
18.868
19.910
20.951
21.991
23.031
24.069
25.106
26.143
27.179
28.214
29.249
30.283
31.316
0.750
χ20.25
1.323
2.773
4.108
5.385
6.626
7.841
9.037
10.219
11.389
12.549
13.701
14.845
15.984
17.117
18.245
19.369
20.489
21.605
22.718
23.828
24.935
26.039
27.141
28.241
29.339
30.435
31.528
32.620
33.711
34.800
0.900
χ20.1
2.706
4.605
6.251
7.779
9.236
10.645
12.017
13.362
14.684
15.987
17.275
18.549
19.812
21.064
22.307
23.542
24.769
25.989
27.204
28.412
29.615
30.813
32.007
33.196
34.382
35.563
36.741
37.916
39.087
40.256
0.950
χ20.05
3.841
5.991
7.815
9.488
11.070
12.592
14.067
15.507
16.919
18.307
19.675
21.026
22.362
23.685
24.996
26.296
27.587
28.869
30.144
31.410
32.671
33.924
35.172
36.415
37.652
38.885
40.113
41.337
42.557
43.773
0.975
χ20.025
5.024
7.378
9.348
11.143
12.833
14.449
16.013
17.535
19.023
20.483
21.920
23.337
24.736
26.119
27.488
28.845
30.191
31.526
32.852
34.170
35.479
36.781
38.076
39.364
40.646
41.923
43.195
44.461
45.722
46.979
0.990
χ20.001
6.635
9.210
11.345
13.277
15.086
16.812
18.475
20.090
21.666
23.209
24.725
26.217
27.688
29.141
30.578
32
33.409
34.805
36.191
37.566
38.932
40.289
41.638
42.980
44.314
45.642
46.963
48.278
49.588
50.892
0.995
χ20.0005
7.879
10.597
12.838
14.860
16.750
18.548
20.278
21.955
23.589
25.188
26.757
28.300
29.819
31.319
32.801
34.267
35.718
37.156
38.582
39.997
41.401
42.796
44.181
45.559
46.928
48.290
49.645
50.993
52.336
53.672
80
8.4
KAPITEL 8. TABELLEN
Kolmogorov Smirnov Test
∆max > Tabellenwert =⇒ Nicht normalverteilt
Anzahl Messwerte N
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
> 35
0.2
0.9
0.68
0.57
0.49
0.45
0.41
0.38
0.36
0.34
0.32
0.31
0.3
0.28
0.27
0.27
0.26
0.25
0.24
0.24
0.23
0.21
0.19
0.18
√
1.07/ N
0.15
0.93
0.73
0.6
0.53
0.47
0.44
0.41
0.38
0.36
0.34
0.33
0.31
0.3
0.29
0.28
0.27
0.27
0.26
0.25
0.25
0.22
0.2
0.19
√
1.22/ N
Signifikanzlevel
0.1
0.05
0.95
0.98
0.78
0.84
0.64
0.71
0.56
0.62
0.51
0.57
0.47
0.52
0.44
0.49
0.41
0.46
0.39
0.43
0.37
0.41
0.35
0.39
0.34
0.38
0.33
0.36
0.31
0.35
0.3
0.34
0.3
0.33
0.29
0.32
0.28
0.31
0.27
0.3
0.26
0.29
0.24
0.27
0.22
0.24
0.21
0.23
√
√
1.36/ N 1.52/ N
0.01
1
0.93
0.83
0.73
0.67
0.62
0.58
0.54
0.51
0.49
0.47
0.45
0.43
0.42
0.4
0.39
0.38
0.37
0.36
0.36
0.32
0.29
0.27
√
1.63/ N
8.5. GRUBBS-TEST (AUSREISSERTEST)
8.5
Grubbs-Test (Ausreissertest)
, ist
P W = |xis−x|
x
n
95%
3
1.154
4
1.481
5
1.715
1.887
6
7
2.02
8
2.127
2.215
9
10 2.29
11 2.355
12 2.412
13 2.462
14 2.507
15 2.548
16 2.586
17 2.62
18 2.652
19 2.681
20 2.708
21 2.734
22 2.758
23 2.78
24 2.802
25 2.822
26 2.841
27 2.859
28 2.876
29 2.893
30 2.908
P W >Tabellenwert(P%,N), so liegt ein Ausreisser vor.
97.5% 99%
1.155
1.155
1.491
1.5
1.742
1.783
1.933
2.02
2.081
2.217
2.201
2.383
2.3
2.524
2.383
2.645
2.455
2.75
2.519
2.843
2.574
2.924
2.624
2.997
2.669
3.063
2.71
3.123
2.748
3.177
2.782
3.226
2.814
3.272
2.843
3.314
2.871
3.353
2.897
3.389
2.921
3.423
2.944
3.455
2.965
3.484
2.986
3.513
3.005
3.539
3.023
3.564
3.041
3.588
3.058
3.61
81
Forschungsprojekte
iGräser App – Pflanzen
bestimmen leicht gemacht
Mit iGräser kann man die 111 häufigsten einheimischen Wald- und Freiland-Grasarten (Poaceae) der Schweiz sowohl im nicht-blühenden als auch im blühenden Zustand einfach,
schnell, zuverlässig und unter Einbezug der
Verbreitungsdaten via GPS-Ortung bestimmen. Die App ermöglicht ein mobiles Lernen
(E-Learning) für die Studierenden.
Im Rahmen des Projektes wurden vom Institut
für Angewandte Simulation mit wissenschaftlich
systematischem Vorgehen «Effiziente Bestimmungsalgorithmen» entwickelt. Die programmtechnische Umsetzung für iPhone und Android
erfolgte ebenfalls am IAS.
Projektpartner:
Institut für Umwelt und Natürliche Ressourcen,
Fachstelle Vegetative Analyse.
Info Flora Schweiz
http://www.igraeser.ch
Institut für Angewandte Simulation ZHAW LSFM
Expertensystem für
Werbeartikel
Prognosesystem für
nachhaltiges Verkehrsmanagement
Das richtige Werbegeschenk zu finden ist
eine langwierige, repetitive Aufgabe. Durch
intelligenten Einsatz von bekanntem Wissen
über die Zielgruppen, Einsicht in die Struktur
des Verkaufsgesprächs und dem Einsatz von
statistischer Programmierung können nun die
Ressourcen von Lieferanten und Käufern besser und zielführender eingesetzt werden, ohne
dabei die Fachkompetenz der Verkäufer ausser Acht zu lassen. Das Resultat ist die vom
IAS in Zusammenarbeit mit der HSG erstellte
Experten-Plattform dayzzi.com.
Die zunehmende Stauhäufigkeit im Verkehr,
die mit grossen Kosten für die Umwelt und
die Gesellschaft verbunden ist, konfrontiert
die Strassenbenutzer/-innen und die Strassenbetreiber mit dem Problem, die Strassennutzung zu optimieren. Dafür braucht es ein
intelligentes Verkehrsmanagement, welches
das Verkehrsgeschehen gesamthaft überblickt
und es erlaubt, die Entwicklung des Verkehrszustandes vorauszusehen. Solche Verkehrsprognosen ermöglichen es, mit frühzeitigen
Massnahmen den Verkehr besser zu verteilen
und gewisse Stauspitzen schon vor der Entstehung zu brechen.
Projektpartner:
Institut für Marketing Universität St.Gallen
dayzzi (Schweiz) AG
Förderung:
Kommission für Technologie und Innovation
KTI
Im Rahmen dieses Projektes werden die Rahmenbedingungen, die ein solches innovatives
Verkehrsprognosesystem erfüllen muss, untersucht und ein entsprechendes System für das
Schweizer Nationalstrassennetz mit den dafür
geeigneten Prognosemethoden und Algorithmen entwickelt.
Projektpartner:
RappTrans AG, Bundesamt für Strassen
ASTRA
Projektförderung:
Bundesamt für Strassen ASTRA
Lehrangebot des IAS
BT
CH
LM
UI
Data Management and Visualisation (T4)
Angebote in
Masterprogrammen
FM
Statistik
Modeling of Complex Systems (T15)
SCM
Biostatistik
Master-Thesis
Informatik
Informatik
Informatik
Informatik
Informatik
Mathematik
Mathematik
Mathematik
Mathematik
Mathematik
Physik
Physik
Physik
Physik
Statistik
Statistik
Statistik
Statistik
Angebote im
BachelorProgramm
SCM
Sys. Eng.
Literaturar.
Semesterarbeiten
Bachelor-Thesis
Vorkurs Mathematik
Vorkurs Physik
Studienvorbereitung
eLearning-Einheit Mathi-Fitnessstudio
eLearning-Einheit Energie
eLearning-Einheit Hydrostatik
eLearning-Einheit Kalorik
Institut für Angewandte Simulation ZHAW LSFM
SCM