Übungen zu Betriebswirtschaftslehre A2: Kostentheorie und
Werbung
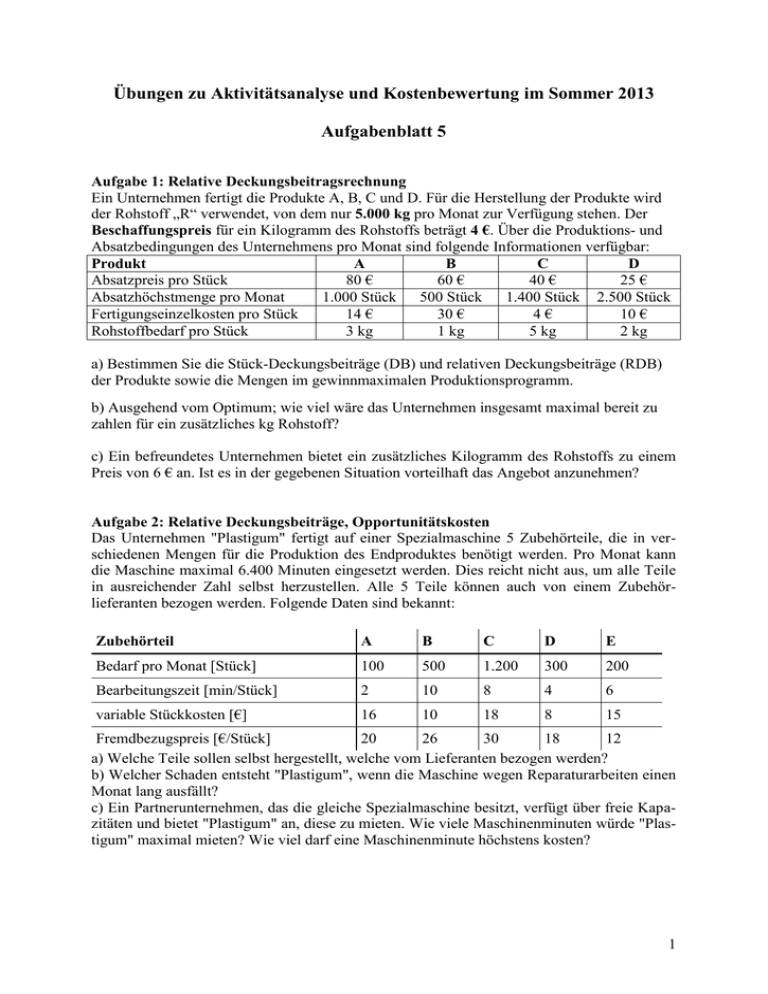
Übungen zu Aktivitätsanalyse und Kostenbewertung im Sommer 2013 Aufgabenblatt 5 Aufgabe 1: Relative Deckungsbeitragsrechnung Ein Unternehmen fertigt die Produkte A, B, C und D. Für die Herstellung der Produkte wird der Rohstoff „R“ verwendet, von dem nur 5.000 kg pro Monat zur Verfügung stehen. Der Beschaffungspreis für ein Kilogramm des Rohstoffs beträgt 4 €. Über die Produktions- und Absatzbedingungen des Unternehmens pro Monat sind folgende Informationen verfügbar: Produkt A B C D Absatzpreis pro Stück 80 € 60 € 40 € 25 € Absatzhöchstmenge pro Monat 1.000 Stück 500 Stück 1.400 Stück 2.500 Stück Fertigungseinzelkosten pro Stück 14 € 30 € 4€ 10 € Rohstoffbedarf pro Stück 3 kg 1 kg 5 kg 2 kg a) Bestimmen Sie die Stück-Deckungsbeiträge (DB) und relativen Deckungsbeiträge (RDB) der Produkte sowie die Mengen im gewinnmaximalen Produktionsprogramm. b) Ausgehend vom Optimum; wie viel wäre das Unternehmen insgesamt maximal bereit zu zahlen für ein zusätzliches kg Rohstoff? c) Ein befreundetes Unternehmen bietet ein zusätzliches Kilogramm des Rohstoffs zu einem Preis von 6 € an. Ist es in der gegebenen Situation vorteilhaft das Angebot anzunehmen? Aufgabe 2: Relative Deckungsbeiträge, Opportunitätskosten Das Unternehmen "Plastigum" fertigt auf einer Spezialmaschine 5 Zubehörteile, die in verschiedenen Mengen für die Produktion des Endproduktes benötigt werden. Pro Monat kann die Maschine maximal 6.400 Minuten eingesetzt werden. Dies reicht nicht aus, um alle Teile in ausreichender Zahl selbst herzustellen. Alle 5 Teile können auch von einem Zubehörlieferanten bezogen werden. Folgende Daten sind bekannt: Zubehörteil A B C D E Bedarf pro Monat [Stück] 100 500 1.200 300 200 Bearbeitungszeit [min/Stück] 2 10 8 4 6 variable Stückkosten [€] 16 10 18 8 15 Fremdbezugspreis [€/Stück] 20 26 30 18 12 a) Welche Teile sollen selbst hergestellt, welche vom Lieferanten bezogen werden? b) Welcher Schaden entsteht "Plastigum", wenn die Maschine wegen Reparaturarbeiten einen Monat lang ausfällt? c) Ein Partnerunternehmen, das die gleiche Spezialmaschine besitzt, verfügt über freie Kapazitäten und bietet "Plastigum" an, diese zu mieten. Wie viele Maschinenminuten würde "Plastigum" maximal mieten? Wie viel darf eine Maschinenminute höchstens kosten? 1 Aufgabe 3: Opportunitätskosten Ein Landwirt kann auf seinen 100 ha Ackerland Weizen (bringt €400 je t bis zu 300t; E = 6), Zuckerrüben (bringen €200 je t, bis zu 450t; E = 15) oder Mais (bringt €250 je t, unbegrenzt; E = 8) (E bedeutet erwartete Erntemenge in t je ha Anbaufläche) anbauen. Kosten je ha Anbaufläche einheitlich: €2100. Nachbarn fragen an, Flächen für Hobbyzwecke zu pachten. a) Ab welcher Pachtrate wird der Landwirt darauf eingehen? b) Was wäre wenn er zu dem Preis von €400 je t bis zu 480 t Weizen verkaufen könnte? Aufgabe 4: Opportunitätskosten und Engpassbewertung Ein Unternehmen produziert Orangensaft aus Orangensaftkonzentrat, das es am Weltmarkt einkauft. Es kann zum Preise von € 0,20 je kg bis zu 170 000 kg Saft pro Woche absetzen. Die variablen Verarbeitungskosten je kg betragen € 0,02. Je kg Erzeugnis werden 0,5 kg Orangensaftkonzentrat benötigt. Am Beginn einer Woche sind 10 000 kg Konzentrat am Lager. Gelagertes Konzentrat muss mit Vitamin C angereichert werden. Das kostet € 0,01 je kg Konzentrat. Folgende Beschaffungsmöglichkeiten bestehen für eine Woche: bis zu 60 000 kg zu € 0,10 je kg bis zu 20 000 kg zu € 0,14 je kg bis zu 100 000 kg zu € 0,16 je kg a) Welche Mengen wird die Unternehmensleitung kaufen, wenn sie in Zukunft fallende Konzentratpreise erwartet? b) Wie hoch ist der Betriebswert eines kg Konzentrat? c) Was ist der Lagerbestand wert? (d.h. wie viel Beschaffungskosten erspart man dadurch, dass man den Lagerbestand schon hat?) Aufgabe 5: Optimale Bestellmenge Der Getränkeproduzent Spritzig vertreibt exklusiv das Sportgetränk "Fit Life", pro Monat werden 2.500 Kisten abgesetzt. Für jede Lieferung verlangt der Fuhrunternehmer unabhängig von der gelieferten Menge 50 €. Zusätzlich fallen pro Kiste und Monat 0,20 € Lagerkosten an. Die jährlichen Zinskosten betragen 10 % auf das durchschnittlich gebundene Kapital. Der Einstandspreis je Kiste beträgt 6 €. a) Ermitteln Sie die optimale Bestellmenge und den optimalen Bestellzyklus in Tagen (d.h. es wird alle ?? Tage eine Bestellung ausgelöst). b) Welchen Preis muss Spritzig für eine Kiste seines Sportgetränks mindestens verlangen, um unter den gegebenen Voraussetzungen kostendeckend zu wirtschaften? 2 Aufgabe 6: Optimale Bestellmenge Pro Periode ist die Nachfrage nach 10.000 Einheiten eines Gutes zu befriedigen. Der Kaufpreis je Einheit dieses Gutes beträgt € 5. Je Lieferung entstehen Kosten von € 40. Die Lagerung einer Einheit kostet € 0.8 je Periode. a) Berechnen Sie die optimale Bestellmenge und die damit verbundene Anzahl von Lieferungen je Periode. b) Die Kostenausgleichseigenschaft der optimalen Losgröße besagt, dass im Bestellmengenoptimum die durchschnittlichen Lagerkosten je Periode den durchschnittlichen Bestellkosten je Periode entsprechen. Zeigen Sie dies für die obigen Parameter. c) Bestimmen Sie die langfristigen Kosten pro Periode (d.h. bei optimaler Anpassung der Losgröße) sowie die Kostenfunktion bei kurzfristig schwankender Bedarfsmenge, wenn die Losgröße auf dem für die Bedarfsmenge von 10.000 Stück optimalen Niveau festgesetzt wird. Aufgabe 7: Losgrößenproblem Ein Autobauer produziert die Kotflügel als Ersatzteile losweise. Die Einrichtung der Presse kostet € 800 je Los. Die Lagerung eines Kotflügels kostet € 4 je Stück pro Monat. Die übrigen variablen Kosten je Stück betragen €10. a) Man bestimme die Kostenfunktion K(x) in Abhängigkeit vom monatlichen Bedarf x. b) Man überlegt, die Produktion fremd zu vergeben. Ein Zulieferer ist bereit, sie zum Preis von € 14 je Stück plus einen Bereitschaftskostenersatz von €300 pro Monat. Für welchen Bereich von x ist das Angebot vorteilhaft? (Hinweis: Ersetzen Sie √x := y, um die Gleichung zu lösen.) c) Bei welcher Bedarfsmenge x° ist der Vorteil der Fremdvergabe gegenüber der Eigenfertigung am größten? Aufgabe 8: Kurz- und langfristige Kostenfunktion Die Produktionsfunktion ist gegeben durch f r1 , r2 30 r1r2 . Der Preis für den ersten Inputfaktor beträgt € 20 je Einheit und € 5 je Einheit für den zweiten Inputfaktor. a) Bestimmen Sie die langfristige Kostenfunktion. b) Bestimmen Sie die kurzfristige Kostenfunktion, wenn der Faktor 1 kurzfristig mit 4 Einheiten fest vorgeben ist. c) Zeichnen Sie lang- und kurzfristige Kostenfunktion in einem Diagramm. d) Für welches Outputniveau sind lang- und kurzfristige Kosten identisch? Bestimmen Sie kurz- und langfristige Grenzkosten sowie kurz- und langfristige Durchschnittskosten an der Stelle dieses Outputniveaus. Interpretation? Aufgabe 9: Kostenfunktionen Ein Beispiel für eine S-förmige Kostenfunktion ist K x 100 4 x 3 36 x 2 110 x a) Bestimmen Sie Durchschnittskostenfunktion, Grenzkostenfunktion und die Funktion der variablen Stückkosten. b) Berechnen Sie das Minimum der variablen Stückkosten und zeigen Sie, dass die Grenzkostenkurve die Kurve der variablen Durchschnittskosten in deren Minimum schneidet. c) Die erwartete Beschäftigung für die Periode sei x P 5 . Führen Sie eine affin-lineare Approximation des Kostenverlaufes durch, indem Sie die Gleichung der Sekante durch die Punkte x 4 und x 6 bestimmen (Schmalenbachs mathematische Kostenauflösung). Bestimmen Sie die (Pseudo-)Fixkosten und die approximativen Grenzkosten. 3 Aufgabe 10: Kostenfunktionen Die Kostenfunktion sei K x 20 x 8 x . Wie hoch sind die approximativen Grenzkosten und die (Pseudo-) Fixkosten bei optimaler affin-linearer Approximation der obigen Kostenfunktion in der Umgebung von x P 10.000 ? Aufgabe 11: Kostenfunktionen Ein Produktionsprozess kombiniert die Faktoren Rohstoff (Einsatzmenge = r1) und Energie (Einsatzmenge = r2). Die Ausbringungsmenge x richtet sich nach folgender Produktionsfunktion: x r1 r2 . Der Rohstoffpreis sei mit p1, der Energiepreis mit p2 bezeichnet. a) Man formuliere das Problem der Bestimmung der Kostenfunktion K(x) als Optimierungsproblem. b) Man bestimme die optimalen Faktoreinsatzmengen in Abhängigkeit von p1, p2 und x. c) Man bestimme die Grenzkostenfunktion und die variablen Durchschnittskosten als Funktion der Ausbringungsmenge. Ist die Kostenfunktion bei gegebenem Faktorpreisverhältnis degressiv, progressiv oder linear? d) Wie wirkt sich eine Steigerung des Energiepreises auf die Grenzkosten aus? e) Angenommen, es können bis zu X Mengeneinheiten zu einem konstanten Verkaufspreis des Produkts ist in Höhe von P abgesetzt werden. Das Unternehmen kann über seine Angebotsmenge x frei entscheiden. Man bestimme die gewinnmaximierende Ausbringungsmenge x*. Aufgabe 12: Kostenfunktionen Die Kostenfunktion einer Unternehmung sei K x 1 x 3 10 x 2 35x . a) Bestimmen Sie an der Stelle x = 4 Grenzkosten, Stückkosten und variable Stückkosten b) Zeigen Sie, dass die Grenzkostenfunktion die Funktion der variablen Stückkosten in deren Minimum schneidet! c) Approximieren Sie K(x) affin-linear durch Schmalenbachs Kostenauflösung durch die Punkte (2,K(2)) und (3, K(3)). Aufgabe 13: Verfahrenswahl Gegeben seien drei Produktionsverfahren mit folgenden Kosten in Abhängigkeit der Ausbringungsmenge x pro Monat: Verfahren A: KA(x) Verfahren B: KB(x) Verfahren C: KC(x) = = = 10 + 4x 20 + 2x 20 + x a) Bestimmen Sie die Kostenfunktion, d.h. die minimalen Kosten in Abhängig der Ausbringungsmenge x. b) Wie ändert sich die Lösung aus a), wenn nun zusätzlich noch Verfahren D zur Verfügung steht: 15 für 0 x 5 K D x 1,5 x für x 5 4 Aufgabe 14: Break Even Analyse In der vergangenen Periode lagen die Gesamtkosten eines Unternehmers bei einer Ausbringung von 15.000 Stück bei 78.000 €. In der Folgeperiode betrug die Ausbringung 12.000 Stück und die Gesamtkosten lagen bei 68.400 €. Der Umsatz betrug in der ersten Periode 72.000 € und in der Folgeperiode 57.600 €. Die Produktionsmittel und die Preise der Produktionsfaktoren blieben unverändert. a) Berechnen Sie die Break Even Menge. Wie hoch sind die Gesamtkosten bei Produktion der Break Even Menge? b) Der Unternehmer möchte nun von Ihnen wissen bei welcher Ausbringungsmenge ceteris paribus ein Gewinn in Höhe von 25% des Umsatzes erreicht wird? Wie hoch sind Umsatz, Gewinn und Gesamtkosten bei Produktion dieser Menge? Aufgabe 15: Verfahrenswahl und Losgröße Ein Unternehmen produziert ein Zwischenprodukt losweise. Die variablen Kosten der laufenden Produktion pro Stück betragen € 100. Die Lagerkosten pro Stück und Jahr betragen € 10, die Auflegungskosten je Los betragen € 1620. Die mit der Produktion befassten Arbeiter schlagen vor, eine Vorrichtung zu beschaffen, die es ermöglichen würde, die Auflegungskosten um 64% zu reduzieren. Die Vorrichtung verursacht jedoch jährliche Kosten in Höhe von € 720. a) Man bestimme die optimale Losgröße in Abhängigkeit vom erwarteten mengenmäßigen Bedarf x° nach dem Zwischenprodukt pro Jahr und zwar für beide Verfahren (mit bzw. ohne Vorrichtung. b) Man bestimme die Gesamtkosten des Zwischenprodukts (einschließlich Auflegungs- und Lagerkosten), in Abhängigkeit vom jährlichen Bedarf x° für den Fall, dass die optimale Losgröße auf den langfristig konstanten Bedarf x° abgestimmt werden kann. c) Für welche Bedarfsmengen ist die Verwendung der Vorrichtung vorteilhaft? d) Wie hoch sind die variablen Stückkosten des optimalen Verfahrens, wenn ein Bedarf von 625 Stück jährlich erwartet wird und darauf auch die Losgröße abgestimmt wird, aber nur 400 gebraucht werden? 5