Kapitel 7 Das Multibutterfly-Netzwerk

Kapitel 7
Das Multibutterfly-Netzwerk
Nachdem wir im vorhergehenden Abschnitt gesehen haben, daß der Ansatz über Oblivious
Routing immer zu einem schlechten Laufzeitverhalten im worst case führt, werden wir in
diesem Abschnitt ein Netzwerk mit konstantem Grad und N = n(log n + 1) Prozessoren
vorstellen: das Multibutterfly-Netzwerk. Es kann mit folgenden Eigenschaften beliebige Permutationen routen:
• Es hat n Eingabeprozessoren und n Ausgabeprozessoren;
• Es benötigt kein Preprocessing;
• Die Puffergröße ist 1;
• Die Routing-Zeit ist O(log n).
Zur Konstruktion dieses Netzwerkes benötigen wir einen sehr interessanten Typ von Netzwerken, nämlich sog. Konzentratoren. Ihnen ist der folgende Abschnitt gewidmet. Sie gehören
zu der Klasse der sog. Expander.
7.1
Konzentratoren
7.1 Definition:
Seien α, β ∈ IR+ , m, c ∈ IN, und sei m eine gerade Zahl. Ein bipartiter Graph G = (A ∪· B, E)
heißt (α, β, m, c)-Konzentrator, falls gilt:
(i) |A| = m, |B| = m/2;
(ii) Knoten aus A haben maximalen Grad c, Knoten aus B haben maximalen Grad 2c;
(iii) (Expansionseigenschaft):
Für alle X ⊆ A, |X| ≤ α · m, gilt: |Γ(X)| ≥ β · |X|
D. h.: Jede Knotenmenge aus A (bis zu einer bestimmten Größe) hat sehr viele Nachbarn
in B. Wir sagen auch, daß A expandiert, und nennen β den Expansionsfaktor.
Wegen der Eigenschaft (iii) gilt α · β ≤ 21 , denn sonst wäre Eigenschaft (i) verletzt.
76
7.1 Konzentratoren
77
Aus solchen Konzentratoren werden wir unser effizientes Routing-Netzwerk konstruieren.
Dazu benötigen wir Konzentratoren mit konstantem Grad und Konstanten α und β, wobei
β > 1 sein muß.
Es ist möglich, Konzentratoren zu konstruieren [LPS88, ?] (sie sind sogar recht einfach),
allerdings sind die Korrektheitsbeweise methodisch sehr aufwendig (Funktionalanalysis und
algebraische Graphentheorie spielen eine wesentliche Rolle), und der resultierende Expansionsfaktor β zwar größer als 1, aber doch nur sehr klein, relativ zu c. Wir werden nun die
Existenz guter Konzentratoren nachweisen.
7.2 Satz:
− 1
1
4β · e1+β c−β−1 gibt es (α, β, m, c)-Konzentratoren.
Für α ≤ 2β
Beweis:
Betrachte die im folgenden definierte Klasse R von bipartiten Graphen G = (A ∪· B, E),
A = [m], B = [m/2].
Für eine beliebige Permutation π : A → A sei Eπ = {(i, j) ∈ A × B | π(i) ∈ {j, j + m/2}}.
Wir erzeugen also durch die Permutation π ein Matching auf einem bipartiten Graphen mit
jeweils m Knoten auf beiden Seiten und klappen“ dann auf einer Seite eine Hälfte der
”
Knoten auf die andere Hälfte der Knoten. Sei R = {G = (A ∪· B, E) | E = Eπ1 ∪ · · · ∪ Eπc
für Permutationen π1 , . . . , πc : A → A}.
Jeder Graph G ∈ R erfüllt durch seine Definition bereits die Bedingungen (i) und (ii) aus
Definition 7.1. Wir zeigen nun, daß es mindestens einen Graphen G ∈ R gibt, so daß für G
auch Bedingung (iii) erfüllt ist.
Dazu betrachten wir das Zufallsexperiment, zufällig unabhängig c Permutationen π1 , . . . , πc
zu wählen. Wir sagen dann: Wir wählen zufällig einen Graphen G ∈ R mit Kantenmenge
Eπ1 ∪ · · · ∪ Eπc .
7.3 Lemma:
Sei G ein zufällig aus R gewählter Graph. Dann gilt:
Prob(G ist kein (α, β, m, c)-Konzentrator) < 1
Vor dem Beweis dieses Lemmas folgern wir zuerst daraus den Satz 7.2:
Wegen Lemma 7.3 ist die Wahrscheinlichkeit, daß ein zufällig aus R gewählter Graph ein
(α, β, m, c)-Konzentrator ist, echt größer als 0. Das heißt aber, daß es in R mindestens einen
(α, β, m, c)-Konzentrator gibt, denn sonst wäre die oben genannte Wahrscheinlichkeit ja 0.
Diese Argumentation ist ein sogenanntes probabilistisches Existenz-Argument. Es ist
sehr elegant, wenn es in erster Linie um die Existenz und nicht um die Konstruktion gewisser Objekte geht. Wie bereits erwähnt, ist es äußerst schwierig, für Graphenfamilien die
Konzentratoren-Eigenschaft nachzuweisen, dagegen ist der Beweis von Lemma 7.3 technisch
relativ einfach. Es wird nur elementares Rechnen benötigt.
2 (Satz 7.2)
Beweis von Lemma 7.3:
In der folgenden Abschätzung wird die Eigenschaft, kein Konzentrator zu sein, genauer formalisiert. Wir berechnen in der Wahrscheinlichkeit gerade das Verhältnis der Zahl an Nicht”
Konzentratoren“ zu der Zahl der Graphen in R überhaupt.
Prob(G ist kein (α, β, m, c)-Konzentrator)
18. Oktober 2005, Version 1.3
7.1 Konzentratoren
78
≤ Prob(∃X ⊆ A, |X| ≤ α · m : |Γ(X)| < β · |X|)
≤ Prob(∃µ ≤ α · m, ∃X ⊆ A, ∃Y ⊆ B : |X| = µ ∧ |Y | = ⌊β · µ⌋ ∧ Γ(X) ⊆ Y )
α·m X
X
X
Prob(Γ(X) ⊆ Y )
≤
µ=1
Y ⊆B
X⊆A
|X|=µ |Y |=⌊β·µ⌋
Seien X ⊆ A und Y ⊆ B mit |X| = µ und |Y | = ⌊β · µ⌋ beliebig aber fest. Wir schätzen
jetzt Prob(Γ(X) ⊆ Y ) ab.
Prob(Γ(X) ⊆ Y )
c
^
= Prob
πi (X) ⊆ Y ∪ {j + m/2 | j ∈ Y }
|
{z
}
i=1
=
≤
c
Y
i=1
c
Y
=: Y ′
Prob(πi (X) ⊆ Y ∪ Y ′ )
µ! ·
2⌊βµ⌋
µ
(da die π1 , . . . , πc unabhängig gewählt sind)
· (m − µ)!
(7.1)
m!
i=1
c Y
2·β ·µ 2·β ·µ−1 2·β ·µ−2
2·β ·µ−µ+1
≤
·
·
· ...·
m
m−1
m−2
m−µ+1
i=1
c
µ
c·µ
Y
2·β ·µ
2·β·µ
≤
=
m
m
i=1
Die Abschätzung (7.1) begründet sich folgendermaßen: Da X und Y fest gewählt sind, fragen
wir nach der Anzahl der Permutationen über A = [m], die X nach Y ∪ Y ′ abbilden. Beachte,
daß wir hier das Hineinklappen der Permutation
πi wieder rückgängig gemacht haben, und
2⌊βµ⌋
′
daß |Y ∪ Y | ≤ 2⌊βµ⌋ ist. Es gibt
Möglichkeiten, Teilmengen der Größe µ in Y ∪ Y ′
µ
zu wählen, und damit µ! · 2⌊βµ⌋
Möglichkeiten, die Werte aus X nach Y ∪ Y ′ abzubilden.
µ
Zusätzlich haben wir (m − µ)! Möglichkeiten, die restlichen Funktionswerte zu wählen. Diese
Zahl wird ins Verhältnis zur Gesamtzahl m! der möglichen Permutationen gesetzt.
Die so berechnete Abschätzung für Prob(Γ(X) ⊆ Y ), die ja nicht von der Wahl von X und
Y abhängt, setzen wir nun ein.
Prob(G ist kein (α, β, m, c)-Konzentrator)
⌊α·m⌋
X X X 2 · β · µ c·µ
≤
m
Y ⊆B
µ=1 X⊆A
|X|=µ |Y |=⌊β·µ⌋
≤
⌊α·m⌋ ≤
⌊α·m⌋ =
X
c·µ
2·β ·µ
m/2
m
·
·
⌊βµ⌋
µ
m
X
e·m
µ
µ=1
µ=1
"
X m
µ
µ=1
⌊α·m⌋
18. Oktober 2005, Version 1.3
µ β·µ c·µ
e · m/2
2·β ·µ
·
·
β·µ
m
#µ
1+β−c
· e1+β · (2 · β)c−β
(s. Lemma 7.4)
7.2 Definition des Multibutterfly-Netzwerks
<
∞ X
µ=1
≤ 1
Das letzte ≤“ gilt, wenn r ≤
”
r≤
1
2
1
2
79
αc−1−β · e1+β · (2β)c−β
|
{z
}
=: r
ist, denn es gilt
∞
X
µ
(da µ ≤ α · m)
( 21 )µ = 1 (unendliche geometrische Reihe).
µ=1
gilt aber wegen der Voraussetzung des Satzes, denn:
1
! c−β−1
c−β−1
1
1
1
1
1
−
α ≤
4β · e1+β c−β−1 =
· e−(1+β)
· ·
2β
2β
2 2β
1
! c−β−1
c−β
1
1
1
= 12 · (2β)−(c−β) · e−(1+β) c−β−1
·
· e−(1+β)
=
2
2β
⇐⇒
1
2
≥ αc−β−1 · (2β)c−β · e1+β = r
2 (Lemma 7.3)
Die oben benutzte Abschätzung für Binomialkoeffizienten wird oft angewandt. Darum soll
sie hier nicht unbewiesen bleiben.
ℓ
7.4 Lemma:
k·e
k
≤
Für k, ℓ ∈ IN, 0 ≤ ℓ ≤ k, gilt:
ℓ
ℓ
Beweis:
∞
X
k · (k − 1) · · · (k − ℓ + 1)
ℓi
kℓ
k ℓ ℓℓ
kℓ ℓ
ℓℓ
k
ℓ
=
≤
= ℓ · ≤ ℓ · e , da e =
≥
gilt.
ℓ!
ℓ!
ℓ ℓ!
ℓ
i!
ℓ!
ℓ
i=0
2
(∗)
{
4β · e
“ der Term (∗) bei konstantem
Man beachte, daß in der Bedingung α ≤
”
β für wachsenden Grad c (sehr schnell) gegen 1 geht, also α·β sehr nah an den größtmöglichen
Wert 12 herankommt.
1
2β
z
}|
1
1+β − c−β−1
7.5 Beispiel:
1
Für β = 2 und c = 4 hat zu gelten α ≤ 32e
3 . Das ist für α =
1
uns dann die Existenz eines ( 643 , 2, m, 4)-Konzentrators.
7.2
1
643
der Fall. Satz 7.2 garantiert
Definition des Multibutterfly-Netzwerks
Aus den gerade vorgestellten Konzentratoren bauen wir jetzt unser Netzwerk, auf dem wir
schnell routen können. Dazu verdoppeln“ wir zuerst die Konzentratoren zu sog. Teilern.
”
7.6 Definition:
Ein (α, β, m, c)-Teiler (oder auch -Splitter) ist ein bipartiter Graph (A ∪·(B0 ∪ B1 ), E0 ∪
E1 ), wobei (A ∪· B0 , E0 ) und (A ∪· B1 , E1 ) jeweils (α, β, m, c)-Konzentratoren sind. Der Grad
eines (α, β, m, c)-Teilers ist 2c. Eine Kante nach B0 heißt 0-Kante, eine nach B1 1-Kante.
18. Oktober 2005, Version 1.3
7.3 Routing im Multibutterfly-Netzwerk
80
A
und
B0
B1
sind Konzentratoren
Abbildung 7.1: Schematischer Aufbau eines Teilers.
Aus den Teilern setzen wir jetzt das Multibutterfly-Netzwerk zusammen:
7.7 Definition:
Das Multibutterfly-Netzwerk MBN(d, α, β, c) hat N = 2d · (d + 1) Knoten und Grad
4c. Abbildung 7.2 zeigt seine rekursive Defintion.
MBN( d,α ,β,c):
MBN( 1,α ,β ,c):
0 1
Quellen
Level 0
d
2 −1
Quellen
( α ,β ,2d,c)-Teiler
Senken
Level 1
Level d
Senken
MBN( d−1, α , β ,c)
MBN( d−1, α , β ,c)
Abbildung 7.2: Rekursive Definition von MBN(d, α, β, c).
Die Knoten auf Level 0 heißen Quellen, die auf Level d Senken von MBN(d, α, β, c). Das
Routing-Problem, das wir betrachten, besteht darin, von jeder Quelle zu genau jeder Senke
genau ein Paket bzgl. einer beliebigen Permutation zu versenden. Der Abstand zwischen einer
beliebigen Quelle und einer beliebigen Senke ist d.
Beachte dabei, daß das Butterfly-Netzwerk BF(d) ein spezielles Multibutterfly-Netzwerk ist
(die Levels sind hier aus technischen Gründen andersherum numeriert), in dem die Teiler
spezielle (1, 12 , m, 1)-Teiler sind, wobei die beiden Konzentratoren je bezüglich der identischen Permutation gebildet sind. Der Expansionsfaktor ist 21 . In unserer Analyse für das
Multibutterfly-Netzwerk werden wir den Expansionsfaktor β > 1 benötigen.
7.3
Routing im Multibutterfly-Netzwerk
Seien α, β, c nun feste Konstanten. n = 2d sei die Zahl der Quellen. Wir werden diese Parameter später genauer spezifizieren. Im folgenden benuzten wir MBN(d) als Abkürzung für
1
MBN(d, α, β, c). Sei L = ⌈ 2α
⌉, und bezeichne Ai die Menge der Pakete mit Zieladresse j,
wobei j mod L = i ist.
Dann haben A0 , . . . , AL−1 je etwa Ln Elemente. In ein Submultibutterfly-Netzwerk MBN(d′ ),
d′ < d, gehören darum höchstens
18. Oktober 2005, Version 1.3
′
2d
L
viele Pakete, jeder der zugehörigen Konzentratoren muß
7.3 Routing im Multibutterfly-Netzwerk
d′
81
′
also nur 12 · 2L ≈ α · 2d Pakete weiterleiten. Das sind aber nach Definition gerade so wenige,
daß sie mit dem Faktor β expandiert werden können.
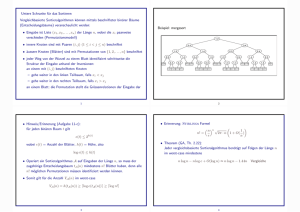
Wir beschreiben zunächst, wie der Weg von den Quellen zu den Senken ungefähr aussieht:
Der Grobe Weg eines Pakets von i = (id−1 , . . . , i0 )2 auf Level 0 nach j = (jd−1 , . . . , j0 )2 auf
Level d geht zuerst über eine jd−1 -Kante, dann über eine jd−2 -Kante usw. Abbildung 7.3 gibt
die Groben Wege in MBN(3) von den Quellen zur Senke (100)2 an.
Quellen
1-Kanten
0-Kanten
0-Kanten
Senken
000 001 010 011 100 101 110 111
Abbildung 7.3: Ein Grober Weg.
Im Butterfly-Netzwerk ist der Grobe Weg gemäß Bemerkung 2.18 (S. 11) und Bespiel 6.5
(S. 61) der einzige Weg von Quelle i nach Senke j, im Multibutterfly-Netzwerk dagegen gibt
es viele mögliche Wege, da es von jedem Knoten aus c viele 0-Kanten und c viele 1-Kanten
gibt. Diese mögliche Auswahl der Wege ist im Butterfly-Netzwerk nicht möglich, weshalb der
Algorithmus über die Groben Wege dort oblivious ist. Sie macht den Algorithmus im MBN
nicht-oblivious.
Routing-Algorithmus für MBN(d):
• Der Algorithmus arbeitet in L Schüben, ein Schub besteht aus einzelnen Runden. Pro
Schub werden ausschließlich die maximal Ln Elemente aus Ak verschickt. Sei k nun fest,
|Ak | ≤ Ln .
• In einer Runde des Routing-Algorithmus für Ak wird folgendes gemacht:
– Jeder Prozessor, der ein Paket hat, ist blockiert. Die Kanten jedes Teilers seien
in 2c Matchings M1 , . . . , M2c zerlegt (Diese Matchings gibt es wegen des Korollars 2.15 zum Heiratssatz).
– for j := 1 to 2c do
Jeder Prozessor, der ein Paket hat, das über eine s-Kante muß für s ∈ {0, 1},
sendet es über eine s-Kante im Matching Mj , falls dort eine solche dabei ist,
und sofern der darüber erreichbare Prozessor nicht bereits blockiert ist.
– Ein Prozessor, der ein Paket bekommt, ist für den Rest der Runde blockiert.
Eine Runde dauert O(c), also konstant viele Schritte.
Wieviele Runden werden benötigt, bis alle Pakete aus Ak bei den Senken auf Level d angekommen sind, d. h. ein Schub beendet ist? Im folgenden werden wir die Zahl der Runden für
einen Schub analysieren.
Sei dazu ein Zeitpunkt t ≥ 0 fest. Wir untersuchen nun die Verteilung der Pakete im Netzwerk,
wir machen also eine Momentaufnahme davon, wo welches Paket nach Runde t ist, und wir
18. Oktober 2005, Version 1.3
7.3 Routing im Multibutterfly-Netzwerk
82
untersuchen, was in der Runde t+1 mit den Paketen passiert: Nach t Runden seien Ki Pakete
auf Level i von MBN(d), 0 ≤ i ≤ d − 1, angekommen. Nach der (t + 1)-ten Runde seien dann
Ki′ Pakete auf Level i, davon mögen bi viele in dieser Runde liegengeblieben (blockiert) und
ai viele hinzugekommen (aktiv) sein. Also ist Ki′ = ai + bi .
Es gelten folgende Beziehungen:
7.8 Lemma:
a) a0 = 0, da auf Level 0 keine neuen Pakete auftauchen können.
b) ai = Ki−1 − bi−1 für i > 0, da auf Level i alle Ki−1 vielen neu hinzu kommen, die vorher
auf Level i − 1 waren, bis auf die bi−1 vielen, die dort liegengeblieben sind.
c) bi ≤
1
β+1
· (Ki+1 + Ki ) für i ≤ d − 2.
d) bd−1 = 0, da alle Pakete auf Level d − 1 sofort weitergeleitet werden, und somit keines
liegen bleibt.
Beweis:
Bis auf die Aussage c) sind alle Punkte bereits begründet.
Zu c):
Betrachte ein Submultibutterfly-Netzwerk MBN(d − i). Seine m = 2d−i Quellen liegen auf
Level i.
Sei z die Zahl der in der Runde t+1 liegengebliebenen Pakete, die über eine 0-Kante (bzw. eine
1-Kante) des durch die 0-Kanten (bzw. 1-Kanten) spezifizierten (α, β, m, c)-Konzentrators
das Level verlassen müssen. z ist höchstens αm, da in das entsprechende MBN(d − i − 1)
nur 12 m/L ≈ αm Pakete hineinwollen. Diese Pakete werden durch mindestens βz Pakete auf
Level i + 1 blockiert, da hier die Expansionseigenschaft gilt. Es gibt in Runde t + 1 höchstens
Ki+1 + ai+1 blockierende Pakete auf Level i + 1, also: β · bi ≤ Ki+1 + ai+1 .
Zusammen ergibt das:
b)
β · bi ≤ Ki+1 + ai+1 = Ki+1 + Ki − bi
⇒ bi · (1 + β) ≤ Ki+1 + Ki
⇒
bi ≤
1
· (Ki+1 + Ki )
1+β
2
Mit Hilfe dieses Lemmas wollen wir die Laufzeitschranke folgern. Dazu benutzen wir eine
Potentialfunktion, die der Situation zur Zeit t, beschrieben durch K0 , . . . , Kd−1 , ein Gewicht zuordnet, oder mit anderen Worten, die die Situation nach der Runde t in einer Zahl
d−1
X
kodiert. Sei ω ∈ (0, 1) beliebig aber fest. Wir definieren Φt :=
Ki · ω i. Dadurch, daß ω < 1
i=0
gilt, wird einer Situation nach Runde t eine um so kleinere Zahl Φt zugeordnet, je näher die
Pakete an ihr Ziel gekommen sind. Φt ist eine Bewertung der Situation.
7.9 Lemma:
a) Φ0 = Ln .
18. Oktober 2005, Version 1.3
7.3 Routing im Multibutterfly-Netzwerk
83
b) Falls ΦT < ω d−1 ist, sind alle Pakete bei den Senken angekommen, d. h. der Schub ist
beendet.
β
1
.
ω + (β+1)·ω
c) Φt+1 ≤ Φt · β+1
Beweis:
Zu a)
Zu Beginn gibt es nur die
ist Φ0 = Ln · ω 0 = Ln .
n
L
Pakete in Level 0, d. h. K0 = Ln , Ki = 0 für i = 1, . . . , d − 1. Also
Zu b)
Falls ΦT < ω d−1 ist, ist ΦT = 0, und somit alle Ki = 0 , d. h. alle Pakete sind auf Level d
angekommen, also am Ziel.
zu c)
Φt+1 =
d−1
X
Ki′ ω i
=
i=0
= b0 + a0 +
|{z}
=0
=
d−1
X
(bi + ai )ω i
i=0
d−1
X
i=1
i
Ki−1 ω +
i=1
d−1
X
d−1
X
(bi + Ki−1 − bi−1 )ω i
d−2
X
i=0
d−2
X
i
i+1
ω d−1
bi (ω
| −{zω }) + |bd−1{z
}
>0
=0
1
(Ki+1 + Ki )(ω i − ω i+1 )
β+1
i=1
i=0
1
1
0
1
= K0 · ω +
(ω − ω )
β+1
1
0
1
1
2
2
(ω − ω + ω − ω )
+ K1 · ω +
β+1
1
3
1
2
2
3
+ K2 · ω +
(ω − ω + ω − ω )
β+1
..
.
1
i−1
i
i
i+1
i+1
(ω − ω + ω − ω )
+ Ki · ω +
β+1
..
.
1
d−1
d−3
d−2
d−2
d−1
+ Kd−2 · ω
+
(ω
−ω
+ω
−ω )
β+1
1
d−2
d−1
(ω
−ω )
+ Kd−1 ·
β+1
1
0
= K0 · ω ω +
(1 − ω)
β+1
1
1
1
−ω
+ K1 · ω ω +
β+1 ω
≤
Ki−1 ω i +
18. Oktober 2005, Version 1.3
(∗)
7.3 Routing im Multibutterfly-Netzwerk
1
β+1
1
ω+
β+1
+ K2 · ω ω +
2
..
.
+ Ki · ω
..
.
i
84
1
−ω
ω
1
−ω
ω
1
1
−ω
ω+
+ Kd−2 · ω
β+1 ω
1
1
d−1
+ Kd−1 · ω
−1
β+1 ω
d−1
X
1
1
i
−ω
≤
Ki ω ω +
β
+
1
ω
i=0
1
1
ω+
= Φt ·
1−
β+1
(β + 1)ω
β
1
= Φt ·
ω+
β+1
(β + 1)ω
d−2
Das bedeutet, daß, wenn
β
ω
β+1
+
1
(β+1)ω
(∗∗)
(wegen ω1 > 1 für (∗) und ω > 0
für (∗∗))
< 1 ist, die Folge der Φt gegen 0 konvergiert.
2
7.10 Satz:
Sei β > 1 beliebig, seien α und c so gewählt, daß für jedes d MBN(d, α, β, c) existiert.
Dann kann MBN(d, α, β, c) beliebige Permutationen von n = 2d Paketen in Zeit O(log n) mit
Puffergröße 1 und ohne Preprocessing routen. MBN(d, α, β, c) hat n(log n + 1) Prozessoren
und Grad 4c.
Beweis:
β
Sei δ := β+1
ω+
1
.
(β+1)ω
Wir müssen gemäß Lemma 7.9 ω ∈ (0, 1) und δ ∈ (0, 1) wählen. Aus der Definition von δ
können wir folgende Beziehung zwischen δ und ω bestimmen:
⇐⇒
⇐⇒
Wähle δ =
√
2 β
.
β+1
1
β
ω+
=δ
β+1
(β + 1)ω
β+1
1
ω2 − δ ·
·ω+ =0
β
β
s
2
1
δ(β + 1)
1 δ(β + 1)
±
−
ω1/2 =
2
β
2β
β
Da β > 1 ist, gilt δ < 1.
p !
1β +1 2 β
1
Dann ist ω =
= √ die einzige Lösung, da der Wurzelterm zu 0 wird.
2 β
β+1
β
Zudem ist ω < 1, da β > 1 ist.
Aus Lemma 7.9 folgt:
18. Oktober 2005, Version 1.3
7.3 Routing im Multibutterfly-Netzwerk
• Zu Beginn ist Φ0 =
n
L
85
;
• in jeder Runde wird Φt um den Faktor δ kleiner, also: Φt ≤
n
L
· δt ;
• für das erste T mit ΦT < ω d−1 gilt: T Runden reichen für einen Schub.
Wir müssen also min{T | ΦT < ω d−1 } bestimmen.
n
L
· δ T < ω d−1
δ T < ω d−1 · Ln
d−1 n
1 T
⇐⇒
> ω1
·L
δ
⇐⇒ T · log 1δ > (d − 1) · log
⇐⇒
Also reichen
T =
&
(d − 1) · log
log
1
+
ω 1
δ
log
n
L
'
1
ω
+ log
n
L
n = O d + log
= O(log n)
L
Runden für einen Schub.
Da wir L Schübe durchführen, ist die Gesamtlaufzeit O(L · log n) = O( logα n ) = O(log n). 2
7.11 Beispiel:
1
In Beispiel 7.5 haben wir gesehen, daß es ( 643
, 2, 2d , 4)-Konzentratoren für beliebige d gibt.
Unsere Parameter wählen wir wie folgt:
√
ω := √12 ≈ 0, 7072
L := 322
δ := 23 2 ≈ 0, 9428
1
, 2, 4) ein Netzwerk mit Grad 16 und für die Zahl T der
Dann haben wir in MBN(log n, 643
Runden je Schub: T ≈ 17, 6549 · log n − 102 bei L = 322 Schüben und einer Dauer von 8
Schritten für eine Runde.
7.12 Bemerkung:
a) Sei N = 2d (d + 1). Enthält jeder Prozessor von MBN(d) ein Paket, so können auch
noch N Botschaften gemäß beliebiger Permutationen π : [N] → [N] in Zeit O(log N)
geroutet werden; p > N viele Botschaften benötigen (optimale) Zeit O( Np + log N).
b) Experimente zeigen, daß das Routing im MBN(d) sehr schnell ist. Bei einer Implementierung kann man ja auch darauf verzichten, das Verfahren in Schüben arbeiten zu
lassen. Die Schübe haben wir nur eingeführt, um die Analyse zu vereinfachen.
c) Ein weiterer Vorteil besteht darin, daß MBN(d) hochgradig fehlertolerant ist. D. h.:
Falls einige Links oder Prozessoren ausfallen, ist die Leistungsfähigkeit des Netzwerks
immer noch sehr gut.
d) Probleme mit der Akzeptanz bei Praktikern: (z. B.: Ingenieure, die Routing Chips bauen) Die Konzentratoren sind unregelmäßig und unstrukturiert; man kann nicht aus
kleinen Konzentratoren einen Großen bauen. Die besten Konzentratoren erhält man,
indem man zufällig Graphen mit passendem Grad auswürfelt“.
”
18. Oktober 2005, Version 1.3
7.4 Literatur zu Kapitel 7
86
7.4
Literatur zu Kapitel 7
[Lei92]
T. Leighton. Methods for message routing in parallel machines. In Proceedings of the 24th
ACM Symposium on Theory of Computing (STOC), pages 77–96, 1992.
[LM92] F. T. Leighton and B. M. Maggs. Fast algorithms for routing around faults in multibutterflies and randomly-wired splitter networks. IEEE Transactions on Computers, 41:578–587,
1992.
[LPS88] A. Lubotzky, R. Phillips, and P. Sarnak. Ramanujan graphs. Combinatorica, 8:261–277,
1988.
[MV97] B. M. Maggs and B. Vöcking. Improved routing and sorting on multibutterflies. In Proc.
29th ACM Symposium on Theory of Computing (STOC), pages 517–530, 1997.
[Par90] I. Parberry. An optimal time bound for oblivious routing. Algorithmica, 5:243–250, 1990.
[Upf92] E. Upfal. An O(log N ) deterministic packet-routing scheme. Journal of the ACM, 39:55–
70, 1992.
18. Oktober 2005, Version 1.3