49. Mathematik-Olympiade 3. Stufe (Landesrunde) Klasse 8

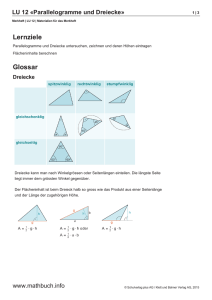
49. Mathematik-Olympiade
3. Stufe (Landesrunde)
Klasse 8
Lösungen – 1. Tag
c 2010 Aufgabenausschuss des Mathematik-Olympiaden e.V.
°
www.mathematik-olympiaden.de. Alle Rechte vorbehalten.
490831 Lösung
6 Punkte
Teil a) Die Legierung enthält (12 kg · 45/100 = ) 5,4 kg Kupfer. In der neu herzustellenden
Legierung sollen diese 5,4 kg nur 40 % des Ganzen darstellen. Die neue Legierung muss also
eine Masse von (5,4 kg : 40/100 = ) 13,5 kg haben. Folglich muss man (13,5 kg − 12 kg = ) 1,5 kg
Zinn hinzufügen.
Um den geforderten Kupfergehalt zu erzeugen, müssen der Legierung 1,5 kg Zinn hinzugefügt
werden.
Teil b) Die Gewichtskraft des Kupfers betrage x N. Dann ist (24 − x) N die Gewichtskraft
des Zinks. Der Kraftverlust im Wasser beträgt laut Aufgabenstellung für Kupfer 1/9 · x N und
für Zink 1/7 · (24 − x) N. Folglich gilt 1/9 · x + 1/7 · (24 − x) = 28/9. Durch Umformen erhält
man 7 · x + 9 · (24 − x) = 182 und schließlich x = 17.
Der Anteil des Kupfers an der Gewichtskraft ist 17/24; der Anteil von Zink ist 7/24.
490832 Lösung
7 Punkte
Nach Voraussetzung sind die Geraden AB, CD
und F G bzw. die Geraden BD, GH und EF parallel. Daher sind die Vierecke P F ED, P GHB,
ABF G und GF CD sowie nach Voraussetzung
ABCD Parallelogramme. Es gelten also
|EF | = |P D|,
|P B| = |GH|,
|AB| = |CD|,
|BC| = |AD|.
A
|<) F EC| = |<) EF P | = |<) DP G|.
C
P
G
(1)
(2)
(3)
Aus dem Wechselwinkelsatz bzw. dem Stufenwinkelsatz an geschnittenen Parallelen folgt
E
D
F
H
B
Abbildung L 490832 a
(4)
Weiterhin sind die Winkel ECF und P GD als gegenüberliegende Winkel im Parallelogramm
GF CD gleich groß, also gilt
|<) ECF | = |<) P GD|.
(5)
Aus dem Innenwinkelsatz sowie (4) und (5) folgt
|<) CF E| = 180◦ − |<) F EC| − |<) ECF | = 180◦ − |<) DP G| − |<) P GD| = |<) GDP |.
Daher und wegen (1) sind die Dreiecke EF C und P DG nach dem Kongruenzsatz (wsw)
kongruent. Folglich haben sie denselben Flächeninhalt; dieser sei mit A1 bezeichnet.
1
Aus dem Wechselwinkelsatz bzw. dem Stufenwinkelsatz an geschnittenen Parallelen folgt
|<) BP F | = |<) P BA| = |<) GHA|.
(6)
Die Winkel HAG und P F B sind als gegenüberliegende Winkel im Parallelogramm ABF G
gleich groß, also gilt
|<) HAG| = |<) P F B|.
(7)
Aus dem Innenwinkelsatz sowie (6) und (7) folgt
|<) AGH| = 180◦ − |<) GHA| − |<) HAG| = 180◦ − |<) BP F | − |<) P F B| = |<) F BP |.
Daher und wegen (2) sind auch die Dreiecke HGA und P BF nach dem Kongruenzsatz (wsw)
kongruent. Folglich haben sie den gleichen Flächeninhalt; dieser sei mit A2 bezeichnet.
Die Dreiecke ABD und CDB haben die gemeinsame Seite BD und sind daher wegen (3)
kongruent nach Kongruenzsatz (sss). Folglich haben auch sie einen gleichen Flächeninhalt;
dieser sei mit A3 bezeichnet.
Folglich haben P F ED und P GHB denselben Flächeninhalt A3 − A1 − A2 .
Lösungsvariante: Der Schnittpunkt der Seite AB mit der Parallelen durch P zur Geraden
BC wird mit K bezeichnet. Der Schnittpunkt der Seite CD mit der Parallelen durch P zur
Geraden BC wird mit L bezeichnet. Dann gelten nach Voraussetzung AB k GF k DC und
BC k KL k AD. Hieraus folgt:
Die Vierecke GP LD, KBF P , AKP G und P F CL sind Parallelogramme.
(1)
Da ein Parallelogramm durch eine seiner Diagonalen stets in zwei (kongruente und daher auch)
flächeninhaltsgleiche Dreiecke zerlegt wird, trifft dies auch für die Dreiecke GP D und LDP
bzw. für die Dreiecke KBP und F P B zu. Die zugehörigen Flächeninhalte bezeichnen wir mit
A1 bzw. A2 (siehe Abbildung L 490832 b).
L
D
D
C
E
C
A1
A1
G
P
A2
G
F
P
F
A2
A
B
K
Abbildung L 490832 b
A
B
H
Abbildung L 490832 c
Das Parallelogramm ABCD wird durch die Diagonale BD in die inhaltsgleichen Dreiecke
ABD und CDB zerlegt, deren Inhalt wir mit A3 bezeichnen. Hieraus und aus (1) folgt:
Die Parallelogramme AKP G und P F CL haben den gleichen Flächeninhalt A3 −A1 −A2 . (2)
Analog wie (1) folgt aus den Voraussetzungen, dass auch die Vierecke HBP G und P F ED
Parallelogramme sind (siehe Abbildung L 490832 c).
Da die Parallelogramme AKP G und HBP G die Seite P G gemeinsam haben und auch in der
Höhe übereinstimmen, sind sie inhaltsgleich. Dasselbe trifft analog für die Parallelogramme
P F CL und P F ED zu. Daher folgt aus (2), dass die Vierecke HBP G und P F ED denselben
Flächeninhalt haben.
2
490833 Lösung
7 Punkte
I. Eine sechsstellige Zahl z mit
z = 100000a + 10000b + 1000c + 100d + 10e + f
schreiben wir kurz als
z = abcdef .
Wenn es eine Zahl z gibt, welche die gestellten Bedingungen erfüllt, dann gelten nach Aufgabenstellung
z = abcdef = 105 · a + bcdef ,
(1)
0
z = bcdef a = 10 · bcdef + a,
z 0 = 3z.
(2)
(3)
Für n = bcdef folgt daher aus (1), (2) und (3)
10n + a = 3 · (105 · a + n),
10n + a = 300000 · a + 3n,
7n = 299999 · a,
also
n = 42857 · a.
Da n eine fünfstellige Zahl sein soll, kann nur a = 1 oder a = 2, also n = 42857 oder n = 85714
gelten.
Wenn es Zahlen z gibt, welche die gestellten Bedingungen erfüllen, dann können dies nur die
Zahlen 142857 oder 285714 sein.
II. Diese beiden Zahlen erfüllen tatsächlich die gestellten Bedingungen, denn sie sind sechsstellig und es gilt 428571 = 3 · 142857 bzw. 857142 = 3 · 285714.
Aus I. und II. folgt, dass es genau zwei Zahlen gibt, welche die gestellten Bedingungen erfüllen,
und zwar 142857 und 285714.
Hinweis: Die Zahl 142857 ist eine Phönix-Zahl: Durch Multiplikation dieser Zahl mit 1, 3,
2, 6, 4 bzw. 5 entstehen Zahlen, welche aus 142857 in dieser Reihenfolge der Multiplikationen
durch zyklisches Vertauschen der Ziffern entstehen, nämlich 142857, 428571, 285714, 857142,
571428, 714285. Außerdem ist 142857 die Periode von 1 bei Division durch 7.
3
Punktverteilungsvorschläge
Die Punktzahlen für die einzelnen Aufgaben sind verbindlich, um Vergleiche z. B. zum Zweck
der Entscheidung über die Teilnahme an der 4. Stufe (Bundesrunde) zu ermöglichen.
Die Einschätzung der Punktzahlen für einzelne Teilschritte einer Schülerlösung (nach dem
Maßstab Verwendbarkeit des Teilschrittes in einem zum Ziel führenden Lösungsweg“) liegt
”
beim Korrektor; die folgenden Aufteilungen sind möglicherweise dem Vorgehen in einer
Schülerlösung anzupassen und können in diesem Sinne gelegentlich abgeändert werden.
Aufgabe 490831
Insgesamt: 6 Punkte
Teil a) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Punkte
Teil b) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 Punkte
Aufgabe 490832
Insgesamt: 7 Punkte
Flächengleichheit der Dreiecke EF C und GP D . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 4 Punkte
Flächengleichheit weiterer Teilflächen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 2 Punkte
Ergebnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Punkt
Aufgabe 490833
Insgesamt: 7 Punkte
Teil I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 Punkte
Teil II . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . 2 Punkte
Ergebnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Punkt
4