Angewandte Elektrotechnik Übungen
Werbung

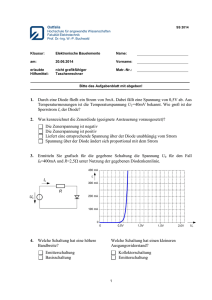
Angewandte Elektrotechnik Übungen Sönke Carstens-Behrens Wintersemester 2009/2010 RheinAhrCampus 1 Übungen 2 Angewandte Elektrotechnik, WS 2009/2010 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen Aufgabe 1: Tiefpass Gegeben ist folgende Schaltung: 10 kΩ Ue 2 nF Ua a) Geben Sie die Übertragungsfunktion der Schaltung an. b) Wie lautet der Amplitudengang? c) Berechnen Sie den Phasengang. d) Wie groÿ ist die Grenzfrequenz fg ? e) Welchen Wert besitzen der Amplitudengang und der Phasengang bei der Grenzfrequenz? Drücken Sie den Wert des Amplitudengangs auch in Dezibel an. f) Zeichnen Sie das Bode-Diagramm der Schaltung. A(ω)/dB 0 −10 −20 −30 −40 −50 −60 −70 −80 100 101 102 103 104 105 106 107 108 109 103 104 105 106 107 108 109 ω s−1 ϕ(ω)/◦ 90 45 0 −45 −90 100 101 102 ω s−1 g) Um wie viel Dezibel pro Dekade nimmt der Amplitudengang im Sperrbereich ab? Hinweis: Dekade bedeutet das Intervall von ω bis 10 · ω. h) Wie groÿ ist der Eektivwert U2 bei einer Kreisfrequenz von ω1 = 1 s−1 , ω1 = 10 s−1 , ω1 = 105 s−1 , ω1 = 107 s−1 , wenn der Eektivwert U1 = 1 V beträgt? RheinAhrCampus, S. Carstens-Behrens 3 Angewandte Elektrotechnik, WS 2009/2010 Übungen Aufgabe 2: RC-Hochpass 1. Ordnung Gegeben ist ein Hochpass 1. Ordnung, der aus einem Widerstand RHP und CHP besteht. a) Geben Sie allgemein die Übertragungsfunktion H(ω), den Amplitudengang A(ω) und den Phasengang ϕ(ω) an. b) Nachfolgend ist der Phasengang des Bode-Diagramms gegeben. Bestimmen Sie draus die Kreisgrenzfrequenz ωg . Hinweis: Beachten Sie, dass die x-Achse die Frequenzen und nicht die Kreisfrequenzen darstellt! c) Welchen Wert besitzt der Kondensator in der vorangegangenen Teilaufgabe, wenn RHP = 1,2 kΩ gilt? d) Zeichnen Sie den Amplitudengang in das Bode-Diagramm ein. A(ω)/dB 0 −10 −20 −30 −40 −50 −60 −70 −80 100 101 f Hz 102 103 104 105 106 107 108 109 102 103 104 105 106 107 108 f Hz 9 10 ϕ(ω)/◦ 90 45 0 −45 −90 100 101 Aufgabe 3: Reihenschwingkreis a) Drücken Sie den komplexen Widerstand eines Reihenschwingkreises, der aus den Elementen R, L und C besteht, mit Hilfe des ohmeschen Widerstandes, der Güte und der Verstimmung aus. b) Wie groÿ sind die Güte und die Bandbreite des Reihenschwingkreises mit R = 10 Ω, L = 200 mH und C = 400 µF? c) Wo liegen die untere und die obere Grenzfrequenzen? 4 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen Aufgabe 4: Parallelschwingkreis Häug werden Parallelschwingkreise als Bandsperren eingesetzt. Bandsperren dämpfen das Eingangssignal in einem bestimmten Frequenzbereich (=Band) stark. Hier ein vereinfachter Aufbau: Lp Rp U in U out Rs Cp a) Berechnen Sie die Übertragungsfunktion der Bandsperre. b) Bei welcher Frequenz wird der Amplitudengang minimal? c) Welchen Wert nimmt der Amplitudengang minimal an? d) Wie groÿ ist der Amplitudengang für ω = 0 und ω → ∞? e) Zeichnen Sie das Bode-Diagramm für Rs = 10 Ω, Rp = 10 kΩ, Cp = 20 nF und Lp = 5 mH. A(ω)/dB 0 −10 −20 −30 −40 −50 −60 −70 −80 100 101 f Hz 102 103 104 105 106 107 108 109 102 103 104 105 106 107 108 f Hz 9 10 ϕ(ω)/◦ 90 45 0 −45 −90 100 101 RheinAhrCampus, S. Carstens-Behrens 5 Angewandte Elektrotechnik, WS 2009/2010 Übungen Aufgabe 5: Transformator Gegeben ist folgende Schaltung mit U 1 = 10 V, f = 50 Hz, R1 = 1 Ω, R2 = 2 Ω, RL = 10 Ω, L1 = 40 mH, L2 = 90 mH und k = 1. Dabei repräsentieren R1 und R2 die ohmschen Widerstände der beiden Spulen des Transformators. I1 R1 R2 I2 U1 RL a) Berechnen Sie die Ströme I 1 und I 2 . b) Berechnen Sie die Schein-, Wirk- und Blindleistung sowie den Leistungsfaktor cos(ϕ) am Eingang. c) Berechnen Sie den Wirkungsgrad. Aufgabe 6: Arbeitspunkt einer Diode Eine Diode habe folgende Kennlinie im Durchlassbereich: I/mA 6 4 2 0 0 0,2 0,4 0,6 0,8 1 U/V Sie wird in Reihe mit einer idealen Spannungsquelle mit U = 1 V und einem Widerstand mit dem Wert R0 = 200 Ω geschaltet: I R0 U UD a) Welcher Strom I und welche Spannung UD stellen sich ein? Lösen Sie das Problem graphisch. b) Welche Leistung fällt an der Diode ab? Aufgabe 7: JFET-Kennlinie Ein JFET-Bauelement, dass eine Übertragungskennlinie und eine Ausgangskennlinie besitzt, wie sie im Skript skizziert sind, wird in eine einfache Schaltung verbaut: 6 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen IDS R1 20 kΩ RD 100 Ω UDS U0 U1 = 16 V UGS R2 10 kΩ Bestimmen Sie die Spannungen UGS , UDS und den Strom IDS sowie die Leistung PD , die am Widerstand RD umgesetzt wird für die beiden Fälle a) U0 = −12 V und b) U0 = −3 V. Hinweis: Verwenden Sie die Kennlinien aus dem Skript. Aufgabe 8: Halbwellengleichrichter Ein Halbwellengleichrichter mit einem Widerstand R = 10 kΩ wird an eine Wechselspannungsquelle mit U 0 = 7 V bei einer Frequenz von f = 50 Hz angeschlossen: i(t) u0 (t) R ua (t) a) Wie groÿ ist die Amplitude û der Spannungsquelle? b) Skizzieren Sie den Spannungsverlauf u0 (t) und die Ausgangsspannung ua (t) für den Fall einer idealen Diode, bei der in Durchlassrichtung keine Spannung abfällt. Achten Sie auf korrekte Achsenbeschriftungen. c) Skizzieren Sie den Verlauf des Stroms i(t). d) Welche Leistung wird am Widerstand im Mittel umgesetzt? Wie hängt diese Leistung von der Frequenz ab? e) Skizzieren Sie den Spannungsverlauf u0 (t) und die Ausgangsspannung ua (t) für den Fall einer (idealen) Diode, bei der im Durchlassbereich eine Spannung von 0,7 V abfällt. Aufgabe 9: Brückengleichrichter Mit einem Brückengleichrichter wird eine Wechselspannung u(t) = û cos(2πf t + π/4), wobei û = 5 V und f = 100 Hz, gleichgerichtet. Der Brückengleichrichter wird mit einem ohmschen Widerstand RL = 100 Ω belastet. Betrachten Sie zur Vereinfachung der nachfolgenden Teilaufgaben die Dioden als ideal, d. h. ohne Spannungsabfall im Durchlassbereich. RheinAhrCampus, S. Carstens-Behrens 7 Angewandte Elektrotechnik, WS 2009/2010 Übungen D1 uD1 (t) D3 i u(t) R ua (t) D2 D4 a) Skizzieren Sie den Spannungsverlauf u(t). b) Welchen Weg nimmt der Stromuss zum Zeitpunkt t = 0 s durch den Gleichrichter und Widerstand? Zeichnen Sie den Pfad in die Schaltung ein. c) Skizzieren Sie die Spannung uD1 (t), die an der Diode D1 abfällt. d) Wie groÿ ist die Momentanleistung p(t), die im Lastwiderstand umgesetzt wird? Welche Leistung P wird im Mittel umgesetzt? e) Nehmen Sie nun an, dass an den Dioden im Durchlassbereich doch eine Spannung abfällt. Was bedeutet das für die Leistung, die am Lastwiderstand umgesetzt wird? Begründen Sie Ihre Antwort. Aufgabe 10: Spannungsstabilisierung mit einer Z-Diode Mit Hilfe einer Z-Diode soll ein Lastwiderstand RL = 160 Ω mit einer stabilisierten Spannung UA = 8 V versorgt werden: RV UE DZ UA RL Dem Datenblatt der Z-Diode ist zu entnehmen, dass für eine Zenerspannung von −8 V ein Zenerstrom von −0,45 A ieÿt. a) Berechnen Sie den Vorwiderstand RV so, dass sich bei einer Eingangsspannung von UE = 10 V eine Ausgangsspannung von UA = 8 V einstellt. b) Wie groÿ sind die Leistungen, die an RV , RL und DZ umgesetzt werden? Aufgabe 11: Stromstabilisierung mit einem JFET In grober Näherung kann im Abschnürbereich eines JFETs von einem konstanten Strom ID = β(UGS − Up )2 ausgegangen werden. β ist der so genannte Transkonduktanz-Koezient. Welchen Wert muss der Widerstand R besitzen, damit ein Strom ID = 5 mA ieÿt, wenn Up = −3,2 V und β = 0,9 mA/V2 sind? Aufgabe 12: Emitterschaltung Gegeben ist eine Emitterschaltung mit kapazitiver Kopplung: 8 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 R1 Ri I1 Übungen RC C2 I2 C1 UBatt U2 U1 uq R2 RE CE RL Dabei sind R1 = 52 kΩ, R2 = 12 kΩ, RC = 540 Ω, RE = 100 Ω, Ri = 600 Ω, RL = 1 kΩ und UBatt = 20 V. Bei dem Transistor handelt es sich um einen 2N2222, dessen Kennlinien im Skript abgebildet sind, siehe Arbeitspunkteinstellung am Beispiel BJT. Die Beschaltung führt zu den beiden Arbeitspunkten: IB = 100 µA, IC = 20 mA. Berechnen Sie die Spannung U 2 am Ausgang für die Eingangsspannung U q = 10 mV. Gehen Sie dabei nach folgenden Teilaufgaben vor: a) Geben Sie die Wechselstromersatzschaltung für Kleinsignalaussteuerung an. b) Bestimmen Sie den Widerstand RBE als den linearen Anteil der Eingangskennlinie im Arbeitspunkt, d. h. bilden Sie das Verhältnis ∆UBE /∆IB . c) Bestimmen Sie den Leitwert GCE entsprechend aus der Ausgangskennlinie im Arbeitspunkt, d. h. bilden Sie her das Verhältnis ∆IC /∆UCE . d) Bestimmen Sie die Stromverstärkung h = IC IB im Arbeitspunkt. e) Bilden Sie eine lineare Ersatzspannungsquelle aus den Elementen R1 , R2 , Ri und U q . f) Wie groÿ ist der Eektivwert IB ? Hinweis: IB ist hier der Eektiwert des Wechselstromes, der durch U q verursacht wird, nicht der Gleichstrom der Arbeitspunkteinstellung! g) Fassen Sie die Widerstande RC , RL und 1/GCE zu einen Widerstand Re zusammen. h) Bestimmen Sie nun die Ausgangsspannung U 2 . Aufgabe 13: Arbeitspunkteinstellung bei Emitterschaltung Der Arbeitspunkt folgender Verstärkerschaltung ist einzustellen. Dabei sollen der Basisstrom IB = 50 µA und die Kollektor-Emitterspannung UCE = 7 V betragen. UB = 15 V RC R1 Ausgang Eingang R2 RheinAhrCampus, S. Carstens-Behrens 9 Angewandte Elektrotechnik, WS 2009/2010 Übungen UBE /V IB /µA 55 50 45 40 35 30 25 20 15 10 5 IC /mA 0,7 0,6 8 0,5 6 0,4 0,3 4 0,2 2 0,1 0 0 10 20 30 40 50 60 IB /µA 0 0 2 4 6 8 UCE /V a) Welche Spannung UBE fällt an der Basis-Emitterstrecke ab? b) Bestimmen Sie die Werte für R1 , R2 und RC . Hinweis: Üblicherweise ist der Strom durch R2 zehnmal so groÿ wie der Basisstrom IB . c) Die Verstärkerschaltung ist temperaturabhängig. Durch welche Maÿnahme kann die Temperaturabhängigkeit verringert werden? Aufgabe 14: Arbeitspunkteinstellung bei Emitterschaltung Betrachten Sie folgende Verstärkerschaltung: UB = 15 V RC R1 Ausgang C1 C2 Eingang R2 RE Der Transistor kann näherungsweise durch folgende Werte beschrieben werden: Die BasisEmitterspannung beträgt UBE = 0,6 V und der Kollektorstrom IC = 200IB . a) Beschreiben Sie die Funktion der beiden Kondensatoren. b) Beschreiben Sie die Funktion der Widerstände. c) Berechnen Sie die Widerstände so, dass sich folgende Werte einstellen: Kollektorstrom: IC = 5 mA Kollektor-Emitterspannung: UCE = 6 V Spannung über RE : URE = 2 V 10 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen Strom durch R2 : IR2 = 10IB Aufgabe 15: Idealer Operationsverstärker Beschreiben Sie folgende Kennzeichen eines idealen Operationsverstärkers: a) Eingangwiderstände b) Ausgangswiderstand c) Dierenzverstärkung d) Eingangsosetspannung e) Anstiegsgeschwindigkeit Aufgabe 16: Realer Operationsverstärker Beim µA741 ist die maximale Anstiegsgeschwindigkeit (slew rate) SR = 0,5 V/µs. Wie groÿ darf die Frequenz bei sinusförmiger Anregung, d. h. uE (t) = ûE sin(2πf t), maximal sein, damit die Ausgangsspannung ebenfalls sinusförmig ist, wenn die Amplitude ûA der Ausgangsspannung a) ûA = 1 V, b) ûA = 10 V. beträgt? Aufgabe 17: Komparator Gegeben ist folgende Operationsverstärkerschaltung: 15 V + ∞ UD − U1 U2 UA −15 V Der Operationsverstärker besitzt folgende Übertragungskennlinie: RheinAhrCampus, S. Carstens-Behrens 11 Angewandte Elektrotechnik, WS 2009/2010 Übungen UA /V 15 −1 UD /mV 1 −15 a) Die Spannung U1 = 8,25 V sei konstant. Wie groÿ ist die Ausgangsspannung für U2 = 0V 4V 8V 8,2 V 8,249 V 8,251 V 8,3 V 10 V b) Erläutern Sie, warum diese Operationsverstärkerschaltung als wird. Komparator bezeichnet Aufgabe 18: Invertierender Verstärker Betrachten Sie folgende Schaltung: R2 I1 U1 R1 − UD + I2 ∞ I2 U2 Es gilt U1 = 1 V, R1 = 10 kΩ und R2 = 20 kΩ. Die Eingangswiderstände des Operationsverstärkers können als unendlich groÿ, der Ausgangswiderstand als unendlich klein betrachtet werden. Berechnen Sie die Spannungen U2 und UD für verschiedene Spannungsübertragungsfaktoren A des Operationsverstärkers: a) A = 105 12 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen b) A = 2 · 105 c) A = 106 Aufgabe 19: Invertierender Verstärker Gegeben ist folgende Schaltung mit einem idealen Operationsverstärker: R2 R1 − U1 ∞ + U2 Ihnen stehen folgende Widerstände zur Verfügung, aber jeweils nur ein Exemplar: 10 kΩ, 47 kΩ, 100 kΩ, 150 kΩ, 220 kΩ, 470 kΩ. a) Um was für eine Schaltung handelt es sich? b) Bestimmen Sie die Widerstände R1 und R2 aus den gegebenen Widerständen so, dass die Schaltung eine Verstärkung von −2 aufweist. c) Wie groÿ sind die Ströme I1 durch den Widerstand R1 und I2 durch R2 , wenn U1 = 3 V? d) Skizzieren Sie das Ausgangssignal für folgendes Eingangssignal: U U1 t e) Skizzieren Sie das Eingangssignal für folgendes Ausgangssignal: RheinAhrCampus, S. Carstens-Behrens 13 Angewandte Elektrotechnik, WS 2009/2010 Übungen U U2 t Aufgabe 20: Strom-Spannungswandler Ein photooptischer Sensor erfasst den Abstand eines Gegenstandes im Bereich von 10 mm bis 100 mm. Als Ausgangsgröÿe liefert er einen Strom zwischen 4 mA und 20 mA. Ein Strom von 4 mA entspricht einer Entfernung von 10 mm, 20 mA einer Entfernung von 100 mm. a) Geben Sie eine Formel für den Strom I(x) in Abhängigkeit des Abstandes x des Gegenstandes zum Sensor an. b) Zur Auswertung steht ein Rechner mit einem Analog-Digital-Wandler (AD-Wandler) zur Verfügung. Ein AD-Wandler wandelt eine Spannung in einen Zahlenwert um, der im Rechner weiterverarbeitet werden kann. Skizzieren Sie eine Schaltung, mit der der Messstrom I(x) in eine Spannung U (x) umgewandelt werden kann. Der AD-Wandler erwartet Spannungen zwischen 0 V und 10 V. Aus einem Strom von 0 A soll also die Spannung 0 V und aus dem maximalen Strom die Spannung 10 V erzeugt werden. Aufgabe 21: Addierer Bei folgender Addiererschaltung sei R2 = 30 kΩ: R1a R2 R1b U1a − U1b + I1 ∞ I1 U2 a) Wie müssen die Widerstände R1a und R1b gewählt werden, damit U2 = − (2U1a + 3U1b ) gilt? b) Wie groÿ ist der Strom IA , der aus dem Ausgang des Operationsverstärkers herausieÿt, wenn die Spannung U2 = 6 V ist? Aufgabe 22: Addieren von drei Spannungen 14 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen a) Entwerfen Sie eine Schaltung, die die drei Spannungen U1 , U2 und U3 gewichtet addiert, so dass sich folgende Ausgangsspannung UA ergibt: UA = −(U1 + 12 U2 + 13 U3 ). b) Weisen Sie rechnerisch nach, dass die Schaltung funktioniert. Aufgabe 23: Subtrahierer Gegeben ist folgende Schaltung: R2 R1 − ∞ + R3 Ua Ub U2 R4 a) Berechnen Sie die Ausgangsspannung U2 folgender Schaltung in Abhängigkeit von Ua und Ub . b) Vereinfachen Sie die Lösung der vorangegangenen Teilaufgabe für den Fall R1 = R3 und R2 = R4 . c) Warum wird diese Schaltung als Subtrahierer oder Subrahierverstärker bezeichnet? Aufgabe 24: Integrierer Gegeben ist die Schaltung eines Integrierers mit einem idealen Operationsverstärker: C R − U1 ∞ + U2 Das Eingangssignal U 1 ist eine Sinusspannung der Frequenz ω . a) Berechnen Sie die Übertragungsfunktion H(ω) = U2 U1 . b) Berechnen Sie den Amplitudengang und den Phasengang. c) Skizzieren Sie das Bode-Diagramm im Intervall 100 ≤ ω ≤ 106 und den Werten R = 10 kΩ und C = 1 µF. Aufgabe 25: Dierenzierer Gegeben ist die Schaltung eines Dierenzierers mit einem idealen Operationsverstärker: RheinAhrCampus, S. Carstens-Behrens 15 Angewandte Elektrotechnik, WS 2009/2010 Übungen R C ∞ − U1 + U2 Das Eingangssignal U 1 ist eine Sinusspannung der Frequenz ω . a) Berechnen Sie die Übertragungsfunktion H(ω) = U2 U1 . b) Berechnen Sie den Amplitudengang und den Phasengang. c) Skizzieren Sie das Bode-Diagramm im Intervall 100 ≤ ω ≤ 106 und den Werten R = 10 kΩ und C = 1 µF. Aufgabe 26: Aktiver Tiefpass Gegeben ist folgende Schaltung eines aktiven Tiefpasses mit RA = 100 Ω, RB = 1 kΩ und C = 1 nF: C RB RA − U1 ∞ + U2 a) Wie lautet die Übertragungsfunktion der Schaltung? b) Geben Sie den Amplitudengang und den Phasengang der Schaltung an. c) Welche Werte besitzen Amplitudengang und Phasengang bei f0 = 0 Hz und f1 = 159,15 kHz und f2 → ∞? d) Skizzieren Sie das Bode-Diagramm. Aufgabe 27: Aktiver Hochpass Gegeben ist folgende Schaltung eines aktiven Hochpasses mit RX = 100 Ω, RY = 1 kΩ und C = 25 nF: 16 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen RY C RX − U1 ∞ + U2 a) Wie lautet die Übertragungsfunktion der Schaltung? b) Geben Sie den Amplitudengang und den Phasengang der Schaltung an. c) Wie groÿ sind die Grenzkreisfrequenz ωg und fg der Schaltung? d) Skizzieren Sie das Bode-Diagramm. Aufgabe 28: Bistabile Kippstufe Skizzieren Sie die Spannungsverläufe der bistabilen Kippstufe für die vorgegebenen Eingangsspannungen. Gehen Sie davon aus, dass die Spannungspulse auf US und UR für einen Schaltvorgang ausreichend groÿ bzw. klein sind. UB RC RC RB RB Q Q T1 UB1 UB2 RS RR US RheinAhrCampus, S. Carstens-Behrens T2 UR 17 Angewandte Elektrotechnik, WS 2009/2010 Übungen US t UR t UB1 0,7 V t UB2 0,7 V t Q UB t Q UB t Aufgabe 29: Monostabile Kippstufe Gegeben ist folgende monostabile Kippstufe: UB 2,2 kΩ 2,2 kΩ 68 kΩ 44 µF 56 kΩ ua ub2 T1 T2 10 kΩ ue a) Geben Sie zwei Bezeichnungen für diese Schaltung an. 18 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen b) Erläutern Sie, warum sich die Zeitkonstante der Schaltung mit tk ≈ RC ln(2) berechnen lässt. c) Skizzieren Sie die Spannungsverläufe von ua und ub2 . Beachten Sie dabei die Zeitskalierung. ue 1 2 3 4 5 6 7 t/s 1 2 3 4 5 6 7 t/s 1 2 3 4 5 6 7 t/s ub2 ua Aufgabe 30: Astabile Kippstufe a) Ergänzen Sie folgende Schaltung zu eine astabile Kippstufe. 470 Ω 4,7 kΩ 4,7 kΩ 470 Ω Q T1 RheinAhrCampus, S. Carstens-Behrens T2 19 Angewandte Elektrotechnik, WS 2009/2010 Übungen b) Legen Sie die geeigneten Bauteile so aus, dass am Q-Ausgang der Kippstufe etwa folgendes Signal entsteht: Q(t) 1 2 3 4 5 6 7 t/ms Aufgabe 31: Analyse von logischen Verknüpfungen mit NAND-Gattern In den nachfolgenden Schaltungen sind digitale Verknüpfungen dargestellt, die nur aus NANDGattern bestehen. Geben Sie für jede Schaltung die Wahrheitstabelle an. Welche logische Verknüpfung wird jeweils dargestellt? a) E1 & & E2 A b) E1 & & E2 A & Aufgabe 32: Synthese von logischen Verknüpfungen mit NAND-Gattern Geben Sie jeweils eine Schaltung an, die folgende Verknüpfung umsetzt, und geben Sie die Wahrheitstabelle gegebenenfalls mit Zwischenschritten an. a) NOT b) NAND c) NOR d) XOR e) XNOR Aufgabe 33: Synthese von logischen Verknüpfungen mit NOR-Gattern Geben Sie folgende logische Verknüpfungen mit Hilfe von Schaltungen an, die nur aus NORGattern bestehen. a) NOT 20 RheinAhrCampus, S. Carstens-Behrens Angewandte Elektrotechnik, WS 2009/2010 Übungen b) AND c) NAND Aufgabe 34: 4-Bit-zu-1-Bit-Datenselektor Ein 4-Bit-zu-1-Bit-Datenselektor besitzt vier Eingänge und einen Ausgang. Jeder Eingang und der Ausgang rerpräsentieren ein Bit. Über zwei Steuerleitungen soll nun ein Eingang ausgewählt und an den Ausgang übertragen werden: Wahrheitstabelle: A B C D Datenselektor S1 0 0 1 1 Z S1 S0 S0 0 1 0 1 Z= A B C D Ergänzen Sie folgende Schaltung zu einem solchen 4-Bit-zu-1-Bit-Datenselektor: S1 S1 S0 S0 A B Z C D & 1 S1 1 S0 Aufgabe 35: Adressdecodierer Zur Ansteuerung verschiedener Bausteine sind so genannte Adressen erforderlich. Eine Adresse ist in der Digitaltechnik eine 1-0-Folge bestimmter Länge, also ein binäres Wort mit einer festgelegten Anzahl von Bits. Es gibt 2-Bit-Adressen, 4-Bit-Adressen, usw. Ein Adressdecodierer ist eine Schaltung, die eine n-Bit-Adresse umsetzt und genau einen von 2n Ausgängen aktiviert. Für einen 2-Bit-Adressdecoder sehen die äuÿere Beschaltung und die Wahrheitstabelle wie folgt aus: RheinAhrCampus, S. Carstens-Behrens 21 Angewandte Elektrotechnik, WS 2009/2010 Übungen Adresseingänge A0 A1 2-BitAdressdecoder Ausgänge QA QB QC QD Wahrheitstabelle: Adresse A1 A0 QA QB 1 0 0 1 0 2 0 1 0 1 3 1 0 0 0 4 1 1 0 0 QC 0 0 1 0 QD 0 0 0 1 Entwerfen Sie eine Schaltung nur mit NOT- und AND-Gattern, die einen 2-Bit-Adressdecoder darstellt. 22 RheinAhrCampus, S. Carstens-Behrens