Arbeitsmaterialen zu Teilchen in Feldern
Werbung

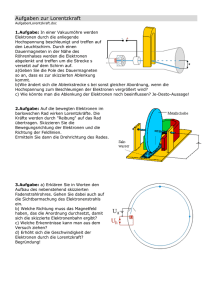
(24. Ergänzungslieferung RAAbits Physik – August 2011 – II/C Reihe 3) Bewegte Ladungen in elektrischen und magnetischen Feldern – ein Stationenzirkel mit Computereinsatz Matthias Borchardt, Bonn Auf einen Klick Hinweise für Lehrerinnen und Lehrer Materialübersicht M1 Elektronen auf Kreisbahn gezwungen – das Fadenstrahlrohr M2 Gefangen – die Erde als magnetische Flasche M3 Mit Fehlern behaftet – magnetische Linsen M4 In der Krebstherapie eingesetzt – das Zyklotron M5 Gekreuzte Felder – die Elektronenablenkröhre M6 Wasserstoff und seine Isotope – das Massenspektroskop Tippkarten Die Erläuterungen und Lösungen finden Sie hier. Zusatzdateien Computersimulationen Bewegte Ladungen in elektrischen und magnetischen Feldern – ein Stationenzirkel mit Computereinsatz Matthias Borchardt, Bonn __________________________________________________________________________ Die Erde als magnetische Flasche für geladene Teilchen, Spulen als Magnetlinsen in Elektronenmikroskopen und Geschwindigkeitsfilter in der Elektronenablenkröhre – die Bewegung von Ladungen in elektrischen und magnetischen Feldern ist spannend, überraschend und mit einem starken Anwendungsbezug verknüpft. Die Schüler erschließen sich die vielfältigen Aspekte dieses Themas mithilfe von Lernstationen, die durch die Verwendung von Computersimulationen besonders anschaulich und handlungsorientiert gestaltet sind. Die Entstehung von Polarlicht Abbildungen im gesamten Beitrag, falls nicht anders angegeben: M. Borchardt Wischer: Der Computer hilft der Anschauung auf die Sprünge! Der Beitrag im Überblick Klasse: 12 Dauer: 6 Doppelstunden Inhalt: – Fadenstrahlrohr Ihr Plus: 7 Simulationsprogramme – Entstehung des Polarlichts – Magnetische Linsen – Zyklotron – Elektronenablenkröhre – Massenspektroskop Fachliche und didaktisch-methodische Hinweise Ein zentrales und für die Abiturprüfung relevantes Thema im Oberstufen-Lehrplan Das Verhalten geladener Teilchen in elektrischen und magnetischen Feldern stellt ein zentrales Thema der Oberstufenphysik dar, das große Relevanz insbesondere für die Abiturprüfung hat. Unbestritten ist, dass der Thematik starke motivierende Impulse innewohnen, die in den vielfältigen Anwendungsbezügen begründet liegen. Elektronenablenkröhre, Fadenstrahlrohr, Linearbeschleuniger, Zyklotron, Synchrotron und das Massenspektroskop werden auf elementarem Niveau im Grund- und Leistungskurs erklärbar und ermöglichen eine Vielzahl attraktiver Rechenaufgaben. Die Schüler merken schnell, wie nah sie mit diesen Unterrichtsinhalten an der modernen Physik sind. Daher finden sie die Stunden endlich wieder interessant, nachdem sie die Durststrecke der Elektro- und Magnetostatik hinter sich gelassen haben, in der sie nicht selten einen lehrerzentrierten Unterrichtsstil erlebt haben. Der Stationenzirkel mit Computereinsatz – nahezu ein reales Experiment Der Stationenzirkel lässt die Schüler selbsttätig in die einzelnen Themen eintauchen. Da an jeder Station eine Computersimulation eingesetzt wird, sind Aufgabenstellungen möglich, die einem realen Experiment nahekommen. Besonders diese aktiven und spielerischen Elemente sind es, die das Arbeiten an den Stationen interessant und spannend machen. Dem Argument, ein echtes Schülerpraktikum sei doch die bessere Alternative, kann man entgegenhalten, dass der Aufbau eines Fadenstrahlrohrs oder einer Elektronenablenkröhre als Schülerexperiment allein aus Sicherheitsgründen problematisch ist (Spannungen: 200– 300 V). Darüber hinaus lassen sich Zyklotron, Massenspektroskop und magnetische Linsen als reales Experiment aus Kostengründen nicht in der Schule verwirklichen. Hier schlägt die Stunde der Computersimulationen, die bei den in diesem Beitrag vorgestellten Lernstationen ein wichtiges Arbeitswerkzeug darstellen. Überschaubar und zeitlich gut zu bewältigen Die Inhalte der Stationen decken einen großen Teil des Lehrplanthemas Bewegung von Ladungen in elektrischen und magnetischen Feldern ab. Dabei ist der Umfang des Stationenzirkels für die Schüler überschaubar und zeitlich gut zu bewältigen. Die ersten drei Stationen behandeln die Bewegung von Ladungen vorwiegend in Magnetfeldern. Erst ab Station 4 kommen Beschleunigungen in elektrischen Längs- und Querfeldern hinzu. Aufgrund der damit verbundenen Progression des Schwierigkeitsgrades erscheint es sinnvoll, bei der Bearbeitung die Reihenfolge der Stationen einigermaßen einzuhalten. Arbeit im Comuterraum der Schule Alle Stationen verlangen eine gezielte Recherche nach Aufbau und Funktion von Geräten, experimentellen Anordnungen und physikalischen Zusammenhängen. Dazu eignet sich oft das eingeführte Schulbuch. Aber auch auf das Internet müssen die Lernenden zugreifen, wenn es beispielsweise um die Entstehung des Polarlichts, Elektronenmikroskope und magnetische Linsen geht, denn nicht alles ist in den gängigen Schulbüchern ausführlich dargestellt. Da die Schüler Computer nicht nur für Rechercheaufträge benötigen, sondern auch für die Ausführung der Simulationen und eine erste Dokumentation ihrer Ergebnisse, ist es ratsam, dass Sie mit Ihrem Kurs im Computerraum der Schule arbeiten. Hinweise zur Gestaltung des Unterrichts Voraussetzungen für die erfolgreiche Durchführung der Unterrichtseinheit Ihre Schüler – sind mit den Grundlagen des elektrischen Feldes vertraut. – kennen die Braun’sche Röhre und den Linearbeschleuniger als Beispiele für die Bewegung von Ladungen in elektrischen Längs- und Querfeldern. – haben die Lorentzkraft (Formel und Drei-Finger-Regel) behandelt und in diesem Zusammenhang das Fadenstrahlrohr kennengelernt. Mithilfe dieses Gerätes wurde gezeigt, dass die Lorentzkraft existiert. Des Weiteren wurde es für qualitative Untersuchungen genutzt, also dafür, dass die Lorentzkraft von der Geschwindigkeit vs senkrecht zu den Feldlinien eines Magnetfeldes und der Stärke der magnetischen Flussdichte dieses Magnetfeldes abhängt. – kennen die Elektronenablenkröhre als Experiment zur Veranschaulichung des Verhaltens von Elektronenstrahlen in sich kreuzenden elektrischen und magnetischen Feldern. Hingegen kennen Ihre Schüler die Formeln rund um das Fadenstrahlrohr und die Elektronenablenkröhre noch nicht, haben an diesen Geräten noch keine Messungen durchgeführt und ausgewertet und auch das Phänomen des Geschwindigkeitsfilters noch nicht untersucht. Diese Aspekte sind Inhalt des Lernzirkels. Stationentische, Geräte, Protokolle und Noten – einige praktische Tipps Wie bereits erwähnt, erscheint es aus sachlogischen Gründen sinnvoll, wenn die Lernenden die Stationen im Wesentlichen in der angegebenen Reihenfolge bearbeiten. Richten Sie jede Station mehrfach ein, damit mehrere Schülergruppen parallel daran arbeiten können, wobei zwei oder drei Mitglieder pro Gruppe eine optimale Wahl darstellen. Jede Lerngruppe gibt nach Abschluss der Stationenstraße eine Mappe mit Protokollen ab, die von Ihnen bewertet wird. Je nach Gruppengröße muss ein einzelner Schüler dann zwei bis drei Protokolle anfertigen. Sie entscheiden, ob Sie die Bewertung der Protokolle auf alle Gruppenteilnehmer gleich verteilen oder lieber individuelle Noten geben. Stellen Sie vorab Fadenstrahlrohr und Elektronenablenkröhre zur Ansicht auf einem Rollwagen bereit. Diese Geräte werden während des Lernzirkels nicht in Betrieb genommen, sondern dienen lediglich zum Zwecke der Anschauung. Da die Computersimulationen frei über das Internet (http://www.mabo-physik.de) zu beziehen sind, können die Schülergruppen auch zu Hause weiterarbeiten, wenn sie aus bestimmten Gründen in Zeitnot geraten sind. Dies sollte jedoch die Ausnahme darstellen, denn es ist wichtig, dass Sie während der Bearbeitung der Stationen als fachlich kompetenter Ansprechpartner zur Verfügung stehen. Computersimulationen Computerprogramme, die im Physikunterricht eingesetzt und vornehmlich von Schülern bedient werden sollen, müssen bestimmte Bedingungen erfüllen: Grundvoraussetzung ist eine Benutzeroberfläche, die übersichtlich ist und eine schnelle und intuitive Bedienung des Programms ermöglicht. Mithilfe der Simulationen sollen die Schüler quantitative Untersuchungen durchführen. Sehr hilfreich kann dafür eine dreidimensionale Darstellung sein, die sich um bestimmte Raumachsen drehen lässt. Besonders die Wirkung der Lorentzkraft führt nämlich oft zu Bahnkurven, die in einer reinen 2-D-Darstellung kaum zu analysieren sind. Auch Größe und Auflösung der Applikationen sind für ihren erfolgreichen Einsatz von Bedeutung. Im Hinblick auf Lernstationen, an denen verschiedene physikalische Inhalte erarbeitet werden sollen, ist es sinnvoll, wenn die eingesetzten Programme alle eine ähnliche Bedienoberfläche besitzen. Eine zusammengewürfelte Sammlung verschiedener Programme mag zwar recht spannend erscheinen, kostet die Lernenden aber viel Zeit und Nerven, weil sie sich in die wechselnde Bedienung der Programme hineindenken müssen. Sieben Computersimulationen auf CD-ROM 24 Sie finden auf der beiliegenden CD-ROM 24 sieben kleine Computersimulationen zum Thema Bewegung von Ladungen in elektrischen und magnetischen Feldern, die speziell auf die Bedürfnisse des Oberstufenunterrichts in Physik zugeschnitten sind, sich gut für eine Einbindung in Lernstationen eignen und alle eine ähnliche Bedienoberfläche besitzen. Sie wurden mit der Programmierumgebung Delphi entworfen und lassen sich auch kostenlos von der Homepage des Autors herunterladen. Es handelt sich um direkt ausführbare Dateien, die nicht extra installiert werden müssen. Sollten Sie sich dafür interessieren, wie man Bewegungen von Teilchen in Kraftfeldern iterativ mithilfe eines Computers berechnet, sind Sie auf den Anhang verwiesen, in dem das Prinzip des Euler-Cauchy-Verfahrens kurz umrissen wird. Bezug zu den Bildungsstandards der Kultusministerkonferenz Wir haben hier die Bildungsstandards für die Sekundarstufe I sinngemäß auf die Oberstufe übertragen, für die Bildungsstandards noch nicht verabschiedet sind. Allg. physikalische Kompetenz Inhaltsbezogene Kompetenzen Die Schüler lernen … Anforderungsbereich … mit Richtung und Betrag der elektrischen Kraft im Sachzusammenhang umzugehen und ihre beschleunigende und ablenkende Wirkung zu verstehen (M 4), I, II … mit Richtung und Betrag der Lorentzkraft im Sachzusammenhang umzugehen und ihre kreisbildende Wirkung zu verstehen (M 1–M 3), I, II F 1–F 4, E 1–E 4, E 7, E 9, K 1–K 5 … verschiedene Kombinationen dieser beiden Kräfte im Sachzusammenhang kennen (M 5), I, II F 1, F 3, E 4, K 1, K5 … wichtige Formeln des Themenkomplexes herzuleiten, zu begründen und zu interpretieren (M 1–M 6), II, III … einen physikalischen Zugang zum Naturphänomen Polarlicht kennen (M 2), II, III … die Abbildungseigenschaften von magnetischen Linsen kennen (M 3), II, III … wichtige Anwendungsbeispiele wie Elektronenmikroskop (M 3), Zyklotron (M 4) und Massenspektroskop (M 6) kennen. I, II F 1–F 4 E 1–E 4, E 7, E 9, K 1–K 5 F 1–F 4 E 1–E 4, E 7, E 9, K 1–K 5 F 4, E 1, E 2, E 4, E 10, K 1–K 3, K 5, B4 F 1, F 3, F 4 E 10, K 1, K 3, K 5 F 2, F 4, E 1–E 3, E 5, K 1–K 5, B 2 Für welche Kompetenzen und Anforderungsbereiche die Abkürzungen stehen, finden Sie vorn im Heft hinter der Inhaltsübersicht. Mediothek http://www.mabo-physik.de (Simulationsprogramme zu den Lernstationen) Außerdem: das eingeführte Schulbuch für die Oberstufenphysik; das Internet und Bücher und Lexika der Schulbibliothek. Zum Fadenstrahlrohr http://www.leifiphysik.de/web_ph10/versuche/10_fadenstrahl/versuch/fadenstrahl.htm Zum Phänomen der Polarlichter http://www.leifiphysik.de/web_ph12/umwelt_technik/02polarlicht/polarlicht.htm http://www.unimarburg.de/fb17/fachgebiete/pflanzenphysio/pflanzenphysiologie_I/forschung/magnetorezeption/ magnetfelder/view http://www.pro-physik.de/Phy/leadArticle.do?laid=10636 Zum Elektronenmikroskop http://www.leifiphysik.de/web_ph10_g8/umwelt_technik/10tem/tem.htm http://www.biologie.uni-hamburg.de/b-online/d03/03e.htm Linsenfehler http://www.uni-mainz.de/FB/Chemie/fbhome/physc/Dateien/Linsen_Korrektur_Schaefer.ppt http://de.wikipedia.org/wiki/Elektronenmikroskop#Optische_Aberrationen_in_Elektronenmikro skopen www.nhn.ou.edu/~larson/SEM/SEM-EMLens-II.ppt http://www.techniklexikon.net/d/elektronenoptische_aberration/elektronenoptische_aberration .htm Zyklotron http://www.leifiphysik.de/web_ph11_g8/umwelt_technik/04teilchenbeschl/zyklotron/prinzip/pri nzip.htm Elektronenablenkröhre Gängige Physikbücher für die Oberstufe (Internetangebot ist sehr rar und wenig informativ) Massenspektroskop http://www.leifiphysik.de/web_ph11_g8/simulationen/04bainbridge/masspe_bainbridge.htm Materialübersicht V = Vorbereitungszeit SV = Schülerversuch Ab = Arbeitsblatt/Informationsblatt D = Durchführungszeit LV = Lehrerversuch Fo = Folie M1 Ab Elektronen auf Kreisbahn gezwungen – das Fadenstrahlrohr V: 5 min D: 90 min M2 Ab Gefangen – die Erde als magnetische Flasche V: 5 min D: 90 min M3 Ab Ab Ab Aufbau, Funktionsweise und Formeln des Zyklotrons; Auswertung Zyklotron.exe Internetzugang, Taschenrechner Gekreuzte Felder – die Elektronenablenkröhre V: 5 min D: 90 min M6 Aufbau und Funktionsweise eines Elektronenmikroskops; Elektronenstrahlen durch kurze Zylinderspulen; Bilddrehung und Linsenfehler Magnetlinse_1.exe Internetzugang Magnetlinse_2.exe Taschenrechner In der Krebstherapie eingesetzt – das Zyklotron V: 5 min D: 90 min M5 Entstehung des Polarlichts; Bewegung von Ladungen in inhomogenen Magnetfeldern Polarlicht.exe Internetzugang, Taschenrechner Mit Fehlern behaftet – magnetische Linsen V: 5 min D: 90 min M4 Aufbau, Funktionsweise und Formeln des Fadenstrahlrohrs (= der Wehnelt-Röhre); Auswertung Fadenstrahlrohr.exe Internetzugang, Taschenrechner Ab Aufbau, Funktionsweise und Formeln der Elektronenablenkröhre; Bewegung von Elektronen in gekreuzten Feldern; Wienfilter; Auswertung Elektronenablenkröhre.exe Internetzugang, Taschenrechner Wasserstoff und seine Isotope – das Massenspektroskop V: 5 min D: 90 min Aufbau, Funktionsweise und Formeln des Massenspektroskops; Auswertung Massenspektroskop.exe Internetzugang, Taschenrechner Die Erläuterungen und Lösungen zu den Materialien finden Sie ab Seite 15. Minimalplan Jedes Material lässt sich auch einzeln in den Unterricht einbauen, wenn Sie das Thema gerade behandelt haben. M 1 Elektronen auf Kreisbahn gezwungen – das Fadenstrahlrohr Aufgaben 1. Informieren Sie sich (Physikbuch, Internet), wie ein Fadenstrahlrohr aufgebaut ist und wie es funktioniert – insbesondere wie der Elektronenstrahl erzeugt, sichtbar gemacht und abgelenkt wird. Der auf dem Rollwagen stehende Versuchsaufbau ist Ihnen dabei ebenfalls von Nutzen. Notieren Sie die wichtigsten Erkenntnisse in Ihren Unterlagen. 2. Starten Sie das Simulationsprogramm Fadenstrahlrohr.exe und machen Sie sich mit den einzelnen Funktionen vertraut. 3. Begründen Sie, dass sich bei eingeschaltetem Magnetfeld eine kreisförmige Bahn für den Elektronenstrahl ergibt. 4. Leiten Sie folgende Formeln her: a) Für die Geschwindigkeit, mit der die Elektronen das Beschleunigungssystem verlassen, gilt: v = 2⋅ e ⋅ Ua ; Ua = Anodenspannung. m b) Für den Radius der Kreisbahn ergibt sich die Formel: r = 2 ⋅ m e ⋅ Ua . e ⋅ B2 5. Stellen Sie im Simulationsprogramm eine kreisförmige Bahn ein und verändern Sie dann die Spannung Ua und die magnetische Flussdichte B. Notieren Sie Ihre Beobachtungen und begründen Sie die Ergebnisse mithilfe der in 4. hergeleiteten Formeln. 6. Man kann das Fadenstrahlrohr dazu verwenden, die Masse von Elektronen zu bestimmen. Voraussetzung ist allerdings, dass die Ladung des Elektrons ( e = 1,6 ⋅ 10−19 C ) bekannt ist. a) Leiten Sie folgende Formel für die Masse des Elektrons her: m e = B2 ⋅ r 2 ⋅e . 2 ⋅ Ua b) Ermitteln Sie mithilfe der Simulation einen Wert für die Elektronenmasse. Tipp Verwenden Sie das Koordinatensystem in der Simulation, dessen Achsen in cm skaliert sind. Für Experten: Wenn Sie die „Elektronenkanone“ im Fadenstrahlrohr etwas schräg stellen (Winkel ≠ 0), entsteht eine spiralförmige Bahn. a) Beschreiben Sie diese Bahn mit Worten und erklären Sie, wie sie entsteht. b) Begründen Sie die folgenden drei Formeln, mit denen sich die Spiralbahn quantitativ erfassen lässt: vr = 2π ⋅r , v z = v r ⋅ tan(φ) , h = v z ⋅ T (*), T wobei r den Radius der Spiralbahn, T die Umlaufzeit für eine Windung und h die Ganghöhe der Spirale bezeichnen. c) Leiten Sie nun mithilfe der drei oben genannten Formeln (*) her: Die Ganghöhe der Spirale ergibt sich aus der Beziehung: h = 2 π ⋅ r ⋅ tan(φ) . d) Überprüfen Sie die Formel h = 2 π ⋅ r ⋅ tan(φ) mithilfe der Simulation. M 2 Gefangen – die Erde als magnetische Flasche Aufgaben 1. Beantworten Sie mithilfe von Physikbüchern und dem Internet die folgenden Fragen: a) Was ist und wie entsteht der Van-Allen-Gürtel der Erde? b) Wie entstehen Polarlichter? c) Warum gibt es manchmal sehr schwache und manchmal sehr intensive Polarlichter? d) Gibt es Polarlichter auch auf anderen Planeten? 2. Wenn geladene Teilchen mit großer Geschwindigkeit schräg auf das Magnetfeld der Erde treffen (siehe Skizze), bewegen sie sich auf schraubenartigen Bahnen Richtung Süd- oder Nordpol. a) Entscheiden Sie, ob das links oben in die Skizze eingezeichnete Teilchen ein positives oder ein negatives Teilchen darstellt. Tipp Stellen Sie sich vor, das Teilchen schraubt sich im Uhrzeigersinn in Richtung des geografischen Nordpols, der in der Abbildung oben liegt, also auf der Seite, auf der man den magnetischen Südpol findet. b) Begründen Sie, dass die Spiralbahn des Teilchens immer enger wird, je näher es dem geografischen Nordpol kommt. c) Erstaunlicherweise endet die Spiralbahn nicht an den Polen. Vielmehr kehrt sich die Schraubrichtung um und das Teilchen bewegt sich von dem einen Pol weg, um dann seine Richtung erneut an dem anderen Pol zu ändern. So können geladene Teilchen für längere Zeit im Magnetfeld der Erde „gefangen“ bleiben. Dieses Phänomen wird als magnetische Flasche bezeichnet. Mithilfe der Abbildung rechts sollen Sie verstehen, wie es zu dieser periodischen Umkehr kommt. Dargestellt sind ein inhomogenes Magnetfeld und eine nach unten führende Schraubenbahn eines Protons. Zeichnen Sie im Punkt P – das Proton geht dort in die Papierebene hinein – die Lorentzkraft als Pfeil ein und begründen Sie, inwiefern das Proton eine Kraft nach oben spürt, welche die Abwärtsbewegung bremst und die Ganghöhe der Spirale vermindert. 3. Eine typische Schraubenbahn ist in der Abbildung unten dargestellt (mit N und S sind hier die magnetischen Pole bezeichnet). Noch eindrucksvoller können Sie die Entstehung solcher Bahnen mithilfe der Computersimulation Polarlicht.exe verfolgen. a) Starten Sie dazu das Programm und machen Sie sich mit dessen Funktionen vertraut. b) Beschreiben Sie kurz, welchen Einfluss die Veränderung der Startparameter auf die Bahn der Teilchen hat. c) Erklären Sie, was die Begriffe Protonendrift und Elektronendrift in der Abbildung unten bedeuten. Für Experten Die geladenen Teilchen (Protonen, Elektronen) stammen von der Sonne (Sonnenwind) und haben Geschwindigkeiten von 300 bis 800 km/s. a) Berechnen Sie, wie lange Teilchen mit einer Geschwindigkeit von 600 km/s in etwa unterwegs sind, bevor sie auf das Magnetfeld der Erde treffen. Tipp Mittlere Entfernung Erde − Sonne: etwa 150 Millionen km. b) Protonen treffen mit einer Geschwindigkeit von 600 km/s in Äquatornähe in einer Höhe von 5000 km senkrecht auf das Erdmagnetfeld. Dort hat es eine Stärke von etwa 5 µT (Mikrotesla). Berechnen Sie, welchen Radius in etwa die Teilchenbahn dort aufweist. Wiederholen Sie die Rechnung für Elektronen. c) Kreis- und Spiralbahnen mit solchen Radien wären in der Computersimulation nicht sichtbar (warum?). Daher wurde im Programm die Geschwindigkeit der Teilchen stark überhöht. Starten Sie die Simulation und „schießen“ Sie Protonen mit einer relativen Geschwindigkeit von 50 senkrecht auf das Erdmagnetfeld (Winkel θ = 90°, ϕ = 0°). Schätzen Sie ab, wie groß der Radius der Spiralbahn ist. Nehmen Sie den Durchmesser der Erde (d = 2 • 6371,04 km) als Bezugsgröße. Berechnen Sie daraus die Geschwindigkeit der Protonen. d) Erklären Sie, warum in der in c) eingestellten Situation keine stabile Kreisbahn (wie beim Fadenstrahlrohr) entsteht, sondern eine flache, spiralförmige Bahn. M 3 Mit Fehlern behaftet – magnetische Linsen Aufgaben 1. Beantworten Sie mithilfe von Physikbüchern und dem Internet, wie ein Elektronenmikroskop aufgebaut ist und wie es funktioniert. Gehen Sie dabei auch auf die Unterschiede zwischen einem Transmissionselektronenmikroskop und einem Rasterelektronenmikroskop ein. 2. Magnetfelder können auf Elektronenstrahlen fokussierende oder defokussierende Wirkung haben. Beim Elektronenmikroskop werden zur Fokussierung der Elektronenbahnen kurze Zylinderspulen verwendet. Die fokussierende Wirkung dieser Spulen ist allerdings schwierig nachzuvollziehen, weil man sich die Situation dreidimensional vorstellen muss. Das Computerprogramm Magnetlinse_1.exe hilft Ihnen, die Funktionsweise dieser magnetischen Linsen zu ver-stehen. a) Starten Sie die Simulation Magnetlinse_1.exe und machen Sie sich mit den Funktionen des Programms vertraut. Schauen Sie sich dazu auch die Info-Box des Programms an. b) Die Linsenwirkung der Spule lässt sich mithilfe der voreingestellten Beispiele in der Simulation nachvollziehen. Beschreiben Sie diese Beispiele kurz in eigenen Worten. Gehen Sie dabei auf folgende Punkte ein: – Welche Art von Elektronenstrahlen treffen auf die Linse (Anfangsbedingungen)? – Was macht die magnetische Linse mit ihnen? – Wie stellt sich die Situation hinter der Linse dar? Gehen Sie dabei auch auf den folgenden Satz ein: Eine typische Eigenschaft magnetischer Linsen ist die Drehung der Bildebene gegenüber der Gegenstandsebene. c) Linsenfehler treten nicht nur bei Glaslinsen, sondern auch bei magnetischen Linsen auf – dort sogar in viel stärkerem Maße. Informieren Sie sich, was man unter chromatischer Aberration und unter sphärischer Aberration bei Glas- und Magnetlinsen versteht, und notieren Sie sich die grundlegenden Inhalte in Ihren Unterlagen. d) Stellen Sie mithilfe der Simulation diese typischen Linsenfehler nach und beschreiben Sie, wie Sie sie erzeugt haben. Illustrieren Sie Ihre Ausführungen auch mit passenden Screenshots der Simulationsergebnisse. e) Recherchieren Sie: Welche Maßnahmen zur Vermeidung der Linsenfehler werden üblicherweise angewendet? 3. Die Drehung und Verzerrung der Bildinformationen beim Durchgang der Strahlen durch die magnetische Linse verändern das Bild des Gegenstandes. Einen Eindruck, wie solche Bilder aussähen, würden Lichtstrahlen ähnlich abgelenkt wie die Elektronenstrahlen in magnetischen Linsen, vermittelt das Programm Magnetlinse_2.exe. Dabei wurde durch ein spezielles Raytracing-Verfahren berechnet, wo die Bildinformationen der einzelnen Bildpixel nach Durchgang durch die magnetische Linse im Auge des Beobachters (Kamera) landen würden. Probieren Sie das Programm aus – Sie können auch eigene Bilder laden und diese durch die Magnetlinse schicken. M 4 In der Krebstherapie eingesetzt – das Zyklotron Aufgaben 1. Informieren Sie sich (Physikbuch, Internet), wie ein klassisches Zyklotron aufgebaut ist und wie es funktioniert. Notieren Sie die wichtigsten Erkenntnisse in Ihren Unterlagen. Fertigen Sie Skizzen an, die die Situation verdeutlichen. 2. Starten Sie das Programm Zyklotron.exe und machen Sie sich mit den Funktionen dieses Programms vertraut. 3. Das Zyklotron hat den großen Vorteil, dass es mit einer Wechselspannung konstanter Frequenz betrieben werden kann. Die Frequenz dieser sinusförmigen Wechselspannung ist durch die berühmte Zyklotronformel gegeben: f = 1 q ⋅ ⋅B 2π m Leiten Sie diese Formel her. 4. Untersuchen Sie mithilfe der Simulation, welchen Einfluss eine Abweichung der Ist-Frequenz von der Soll-Frequenz auf die Bahn der geladenen Teilchen hat. Zyklotron in der University of Washington – eingesetzt in der Krebstherapie Foto: http://de.wikipedia.org 5. Lassen Sie ein Ion das Zyklotron vollständig durchlaufen und betrachten Sie danach die Kurven, welche die zeitliche Entwicklung der Geschwindigkeit und die der Energie angeben. Beschreiben Sie die Form der Kurven. Worin unterscheiden sich die beiden Kurven deutlich voneinander? Erklären Sie, warum dies so ist. 6. Wenn der Krümmungsradius des letzten Halbkreises der Teilchenbahn mit rEnd bezeichnet wird, gibt die folgende Formel die kinetische Energie des Teilchens auf diesem Halbkreis an: EkinEnd = q 2 ⋅ B2 ⋅ rEnd 2 2 ⋅m Leiten Sie diese Formel her. 7. Bemerkenswert an dieser Formel ist, dass die Endenergie nicht von der Höhe der angelegten Beschleunigungsspannung Ua abhängt. Machen Sie diese Aussage physikalisch plausibel. Tipp Lassen Sie in der Simulation Ionen bei verschiedenen Spannungen (aber konstantem Magnetfeld) das Zyklotron durchlaufen und betrachten Sie die Bahnkurven. 8. Da der Krümmungsradius des letzten Halbkreises nicht mit dem Radius des Zyklotrons übereinstimmt und das Programm keine Informationen über die Radien der Halbkreise liefert, lässt sich die Endenergie hier nicht mit der Formel aus 6. berechnen. Das Programm gibt allerdings die Endgeschwindigkeit der Teilchen beim Verlassen des Zyklotrons an. Beschleunigen Sie hintereinander ein Proton, einen Deuteriumkern und einen Heliumkern (bei gleichen Parametern des Zyklotrons) und berechnen Sie die Endenergien der Teilchen in Elektronenvolt (eV). Tipp Einstellungen: Ua = 2500 V, B = 0,1 T. M 5 Gekreuzte Felder – die Elektronenablenkröhre Aufgaben 1. Informieren Sie sich (Physikbuch), wie eine Elektronenablenkröhre aufgebaut ist und wie sie funktioniert – insbesondere wie der Elektronenstrahl erzeugt, sichtbar gemacht und abgelenkt wird. Der auf dem Rollwagen stehende Versuchsaufbau ist Ihnen dabei ebenfalls von Nutzen. Notieren Sie die wichtigsten Erkenntnisse in Ihren Unterlagen. 2. Starten Sie das Simulationsprogramm Elektronenablenkröhre.exe und machen Sie sich mit den Funktionen dieses Programms vertraut. 3. Lassen Sie das Magnetfeld ausgeschaltet und stellen Sie eine Ablenkspannung ein, die zu einer deutlich gekrümmten Bahn führt. Stellen Sie den Strahl so ein, dass im Koordinatensystem die Koordinaten eines Punktes der Bahn gut ablesbar sind. Prüfen Sie nun durch Rechnung, ob die von der Braun’schen Röhre her bekannte Formel y = 1 e UK 1 2 ⋅ ⋅ ⋅ ⋅ x mit v 0 = 2 m d v 20 2⋅ e ⋅ Ua m hier auch gilt (d = 0,1 m). 4. Nun soll die Ablenkspannung gleich 0 sein. Schalten Sie nur das Magnetfeld ein. a) Der Radius des kreisförmigen Bahnabschnitts lässt sich mit der Formel r = m ⋅ v0 e ⋅B berechnen. Leiten Sie diese Formel her. b) Überprüfen Sie die Formel mithilfe der Simulation (ein Beispiel genügt). Protokollieren Sie die gewählten Einstellungen und Ergebnisse. 5. Mit der Elektronenablenkröhre kann man das Prinzip eines Geschwindigkeitsfilters für geladene Teilchen demonstrieren. a) Wählen Sie in der Simulation eine Ablenkspannung und versuchen Sie durch Variation des Magnetfeldes, den Strahl wieder gerade zu „biegen“. Notieren Sie die Polung des elektrischen und magnetischen Feldes (mithilfe einer Skizze) und die eingestellten Werte. b) Leiten Sie folgenden Zusammenhang her: Für den Fall, dass die Wirkungen der beiden Felder auf die bewegte Ladung sich gegenseitig aufheben (gerader Strahl), gilt: v = E . B c) Überprüfen Sie diese Formel mithilfe der Simulation. Protokollieren Sie die gewählten Einstellungen und Ergebnisse. d) Nehmen Sie an, die „Elektronenkanone“ ist nicht in der Lage, allen Elektronen exakt die gleiche Geschwindigkeit zu geben. Diskutieren Sie: Was geschieht mit Elektronen, die etwas zu langsam sind, bzw. solchen, die etwas zu schnell sind? Erläutern Sie in diesem Zusammenhang, warum man diese Anordnung als Geschwindigkeitsfilter (Wienfilter) bezeichnet. M 6 Wasserstoff und seine Isotope – das Massenspektroskop Aufgaben 1. Informieren Sie sich (Physikbuch, Internet), wie ein Massenspektroskop (Massenspektrograf, Massenspektrometer) nach Bainbridge aufgebaut ist und wie es funktioniert. Notieren Sie die wichtigsten Erkenntnisse in Ihren Unterlagen. 2. Starten Sie das Simulationsprogramm Massenspektroskop.exe und machen Sie sich mit den Funktionen dieses Programms vertraut. 3. Die Masse m der Teilchen und ihre Bahnradien r im Ablenkfeld B2 sind zueinander proportional. Es gilt die Beziehung: q ⋅ B1 ⋅ B2 ⋅ d m = ⋅r UK Prinzip des Massenspektroskops Quelle: http://www.leifiphysik.de/web_ph12/musteraufgaben/0 2beweg_gel_teil/massenspektro_00/anordnung.gif Leiten Sie diese Formel her. Tipp Verwenden Sie Ihre Erkenntnisse aus Station 5 über den Geschwindigkeitsfilter. 4. Überprüfen Sie diese Formel mithilfe der Simulation durch ein konkretes Beispiel. Protokollieren Sie die gewählten Einstellungen und Ergebnisse (q = 1,6 • 10–19 C). Für Experten: Wasserstoff und seine Isotope Bestimmen Sie die Massenverhältnisse von Wasserstoff und den Isotopen Deuterium und Tritium zueinander. Stellen Sie eine Beschleunigungsspannung von 600 Volt ein und wählen Sie einen scharfen Geschwindigkeitsfilter (hohe Feldstärken: beispielsweise B1 = 0,06 T). a) Wählen Sie zunächst Tritiumkerne als Teilchenart. Stellen Sie den Geschwindigkeitsfilter so ein, dass die Ionen geradlinig den Filter passieren, und wählen Sie das Magnetfeld B2 so, dass ein großer Halbkreis entsteht. Notieren Sie sich die Werte – vor allem den Radius des Halbkreises. b) Wählen Sie nun Deuterium. Lassen Sie das Feld B2 und den Geschwindigkeitsfilter unangetastet (warum?) und variieren Sie nur die Beschleunigungsspannung Ua so lange, bis die Deuteriumkerne den Geschwindigkeitsfilter geradlinig durchlaufen. Bestimmen Sie den Radius der Halbkreisbahn. c) Führen Sie die oben beschriebenen Schritte auch mit Wasserstoff durch. d) Welche Aussage können Sie nun aus den Radien der Halbkreise bzgl. des Massenverhältnisses der drei Teilchenarten zueinander machen? Tippkarten für die Differenzierung nach Grund- und Leistungskurs Die Stationen wurden für einen Leistungskurs konzipiert, Sie können sie aber auch gut in einem Grundkurs einsetzen. Dazu ist es ratsam, die Stationen mit einigen Hilfestellungen zu versehen und sie etwas zu reduzieren. Falls Sie den Lernzirkel in einem Grundkurs verwenden möchten, teilen Sie die folgenden Tippkarten an die Lernenden aus: M1 Elektronen auf Kreisbahn gezwungen – das Fadenstrahlrohr Aufgabe 4 a) Verwenden Sie den Ansatz: Die Arbeit, die das elektrische Feld am Elektron verrichtet, wird vollständig in kinetische Energie umgewandelt. b) Verwenden Sie den Ansatz: Die Lorentzkraft wirkt hier als Zentripetalkraft. Aufgabe für Experten, Teil d) Stellen Sie dazu beispielsweise einen Winkel von 3,3° ein. Wählen Sie das Magnetfeld dann so, dass die Spiralbahn eine Ganghöhe von genau 2 cm hat. Nun können Sie den Radius r der Spiralbahn ablesen, wenn Sie eine günstige Beobachtungsposition wählen. M4 In der Krebstherapie eingesetzt – das Zyklotron Aufgabe 3 Verwenden Sie den Ansatz: Die Lorentzkraft wirkt hier als Zentripetalkraft. Zwischen Geschwindigkeit und Umlauffrequenz besteht folgender Zusammenhang: v = 2π ⋅r =2π ⋅r ⋅ f T Aufgabe 5: Verwenden Sie die Formel für die kinetische Energie. M5 Gekreuzte Felder – die Elektronenablenkröhre Aufgabe 4a) Verwenden Sie den Ansatz: Die Lorentzkraft wirkt hier als Zentripetalkraft. Aufgabe 5b) Bedenken Sie: Der Elektronenstrahl wird nur dann geradlinig verlaufen, wenn sich die elektrische Feldkraft und die Lorentzkraft kompensieren. M6 Wasserstoff und seine Isotope – das Massenspektroskop Aufgabe 3 In Station 5 haben Sie gelernt, dass nur Teilchen den Geschwindigkeitsfilter durchlaufen, deren Geschwindigkeit der Bedingung v = E genügt. Außerdem gilt: B1 Im Magnetfeld B2 wirkt die Lorentzkraft als Zentripetalkraft. Erläuterungen und Lösungen M1 Elektronen auf Kreisbahn gezwungen – das Fadenstrahlrohr Zur Bearbeitung dieser Station ist es hilfreich, wenn die Schüler den experimentellen Aufbau des Fadenstrahlrohrs bereits aus dem Unterricht kennen und er ihnen zum Anschauen auch während der Stationsbearbeitung zur Verfügung steht. Verzichten Sie jedoch in dieser Phase auf eine Inbetriebnahme der Anordnung, denn die notwendige Verdunkelung des Raumes und Ihre ständige Anwesenheit (Sicherheitsaspekte) verhindern eine zügige Bearbeitung der Station. Wenn Sie mit dem gesamten Kurs im Computerraum der Schule arbeiten, stellen Sie das Fadenstrahlrohr (ohne elektrische Beschaltung) zur Ansicht auf das Lehrerpult. Lösungen 3. Die Geschwindigkeit der Elektronen ist betragsmäßig nahezu konstant und senkrecht zum Magnetfeld gerichtet, das in Betrag und Richtung zeitlich konstant ist. In jedem Punkt der Bahn innerhalb des Feldes ist der Betrag der Lorentzkraft daher gleich. Außerdem ist sie stets senkrecht zum Geschwindigkeitsvektor und zur magnetischen Flussdichte gerichtet – die Lorentzkraft wirkt also als kreisbildende Kraft. 4. a) Für die Beschleunigung der Elektronen in der „Elektronenkanone“ gilt: Die Arbeit, die das elektrische Feld am Elektron verrichtet, wird vollständig in Bewegungsenergie umgewandelt. e ⋅ Ua = 21 m ⋅ v 2 ⇔ v = 2⋅ e ⋅ Ua m b) Die Lorentzkraft wirkt als Zentripetalkraft – daher gilt: FL = FZ ⇔ e ⋅ v ⋅ B = m ⋅ v2 r r= m ⋅v (I) e ⋅B Setzt man die in Teil a) gefundene Formel für v ein, ergibt sich: m ⋅v r= = e ⋅B m⋅ e ⋅ Ua m = e ⋅B 2⋅ 2 ⋅ m ⋅ Ua (II) e ⋅ B2 5. Man erkennt: – Je größer die Beschleunigungsspannung Ua ist, desto größer ist der Radius r der Kreisbahn. – Je größer die magnetische Flussdichte B ist, desto kleiner ist der Radius r der Bahn. Beide Aussagen lassen sich durch die Formel (II) belegen, weil Ua im Zähler des Bruches steht und B im Nenner. 6. a) Umstellen der Formel (II) nach m ergibt die gesuchte Formel: m e = B2 ⋅ r 2 ⋅ e (III) 2 ⋅ Ua b) In der Simulation wurden z. B. folgende Werte eingestellt: Ua = 253 V und B = 0,000715 T und Winkel = 0°. Damit ergibt sich ein Radius der Elektronenbahn von 7,5 cm. Eingesetzt in die Formel aus (III) ergibt sich für die Masse des Elektrons: 9,0929 ⋅ 10−31 kg Für Experten a) Es entsteht eine Spiralbahn mit konstantem Radius und konstanter Ganghöhe. Die Geschwindigkeit der Elektronen lässt sich nämlich in zwei Komponenten zerlegen: Die Komponente senkrecht zu den magnetischen Feldlinien ist für die Lorentzkraft verantwortlich. Diese zwingt das Elektron auf eine kreisförmige Bahn, die Komponente parallel zu den Feldlinien trägt zur Lorentzkraft nichts bei, sondern bewirkt eine gleichförmige Bewegung längs der z-Achse. Beide Komponenten zusammen zwingen das Elektron auf eine Spiralbahn. b) v r ist die Geschwindigkeit, die das Elektron in der x-yEbene hat, also auf dem Kreis, der sich als Projektion der Spiralbahn auf diese Ebene ergeben würde. Für einen Umlauf 2 π ⋅ r benötigt das Elektron die Zeit T. v z = v r ⋅ tan(φ) ergibt sich direkt aus der Geometrie des Vek- tordiagramms. Die Ganghöhe h ergibt sich aus der Definition der Ganghöhe: Das Elektron bewegt sich mit der Geschwindigkeit vz in z-Achsen-Richtung innerhalb der Zeit T um die Ganghöhe h weiter. c) Mithilfe der drei Formeln leitet man her: h = v z ⋅ T = v r ⋅ tan(φ) ⋅ T = 2π ⋅r ⋅ tan(φ) ⋅ T = 2 π ⋅ r ⋅ tan(φ) T d) Einstellung: Ua = 250 V, B = 0,00095 T, Winkel: φ = 3, 3o . An der z-Achse (Einteilung in cm) liest man ab, dass die Spirale eine Ganghöhe von 2 cm hat. An der x-Achse (Einteilung in cm) liest man ab, dass der Kreis einen Durchmesser von 11,1 cm hat. Also beträgt der Radius der Spirale r = 5,55 cm. Die Formel ergibt für die Ganghöhe: h = 2 π ⋅ r ⋅ tan(φ) = 2 π ⋅ 0,0555 m ⋅ tan(3, 3°) = 0,0201m ≈ 2 cm Damit ist die Formel bestätigt. M2 Gefangen – die Erde als magnetische Flasche Das Computerprogramm Polarlicht.exe simuliert die Bahnen von Protonen und Elektronen im Magnetfeld der Erde und zeigt sehr eindringlich, welchen Einfluss Auftreffwinkel und Auftreffgeschwindigkeit auf die Form der Spiralbahnen haben. Darüber hinaus zeigt die Simulation das Pendeln der Teilchen zwischen Nord- und Südpol und vermittelt so eine sehr anschauliche Darstellung des Phänomens magnetische Flasche. Aus didaktischen Gründen wurde die Geschwindigkeit der ankommenden Teilchen deutlich überhöht, da die Durchmesser der Spiralbahnen sonst so klein ausfallen würden, dass sie im Vergleich zur abgebildeten Erdkugel nur als Striche wahrnehmbar wären. Diese Problematik wird in Form einer Aufgabe für Experten am Ende der Station thematisiert. Weisen Sie Ihre Schüler darauf hin, dass sie, um Unklarheiten zu vermeiden, in ihren Ausführungen zwischen geografischem Nord- und Südpol und magnetischem Nord- und Südpol unterscheiden sollen. Lösungen 1. a) Der Van-Allen-Gürtel ist ein torusförmiger Landungsspeicher, der die Erde umgibt und in dem vom Sonnenwind stammende geladene Teilchen eingefangen werden. Das Erdmagnetfeld ist auf der sonnenabgewandten Seite aufgrund dieser Teilchenstrahlung wie ein Kometenschweif verformt, was in der Skizze auf dem Arbeitsblatt jedoch nicht berücksichtigt wurde. b) http://www.leifiphysik.de/web_ph12/umwelt_technik/02polarlicht/polarlicht.htm c) Das liegt daran, dass die Aktivität der Sonne schwankt (in etwa ein 11-Jahres-Zyklus). Bei großer Sonnenaktivität ist der Sonnenwind entsprechend intensiv und es gelangen viele Teilchen in das Magnetfeld der Erde. d) http://www.pro-physik.de/Phy/leadArticle.do?laid=10636 2. a) Mithilfe der Drei-Finger-Regel der linken Hand (im Punkt P) stellt man fest, dass es sich um ein negativ geladenes Teilchen handeln muss. 2. b) In Richtung der Pole wird das Magnetfeld stärker. Wegen r = m ⋅v (siehe Station 1, e ⋅B (I)) bewirkt eine Vergrößerung der magnetischen Flussdichte eine Verringerung des Radius der Teilchenbahn – d. h. die Bahn wird immer enger. 2. c) Die Richtung der Lorentzkraft ergibt sich durch Anwendung der Drei-Finger-Regel für die rechte Hand (Proton). Die Lorentzkraft ist schräg nach oben gerichtet, was dazu führt, dass das Teilchen nicht nur auf die Kreisbahn gedrückt wird, sondern auch nach oben. Die Abwärtsbewegung wird dadurch gebremst bzw. schließlich in eine Aufwärtsbewegung verwandelt. 3. b) Die Veränderung des Startparameters hat z. B. folgenden Einfluss auf die Bahn: Eine Erhöhung der Startgeschwindigkeit der Teilchen führt zu Spiralbahnen mit einem deutlich größeren Radius. Die Wanderung der Teilchenbahnen nach Westen bzw. Osten wird ebenfalls stärker. Treffen die Teilchen steiler in der Region des Äquators auf (wenn der Winkel θ zugenommen hat), kommen sie den Polen nicht mehr so nahe – sie kehren früher um. c) Die Simulation zeigt, dass positiv geladene Teilchen (Protonen) nach links – wenn man von oben auf den geografischen Nordpol schaut, im Uhrzeigersinn – wegdriften, während negativ geladene Teilchen gegen den Uhrzeigersinn wandern. Für Experten a) Entfernung Erde − Sonne: etwa 150 000 000 km. Teilchen mit einer Geschwindigkeit von 600 km/s benötigen dafür 250 000 Sekunden. Das sind nahezu 70 Stunden. Die Laufzeit der Teilchen liegt daher zwischen 2 und 3 Tagen. b) Protonen: r = Elektronen: r = m ⋅ v 1,67 ⋅ 10−27 ⋅ 600 000 = m = 1252,5 m e ⋅B 1, 6 ⋅ 10−19 ⋅ 5 ⋅ 10−6 m ⋅ v 9,1⋅ 10−31 ⋅ 600 000 = m = 0,6825 m e ⋅B 1, 6 ⋅ 10−19 ⋅ 5 ⋅ 10−6 c) Bahnen mit solchen Radien würden im Vergleich zur Erdkugel in der Simulation so schmal erscheinen, dass man sie nicht mehr als Spirale erkennen könnte. Mit den angegebenen Einstellungen entsteht eine flache Spiralbahn, die sich um den Äquator bewegt. Um dies zu erkennen, sollte man die Erdkugel von oben mit Blick auf den Nordpol betrachten (siehe Screenshot). Geschätzt beträgt der Durchmesser der Spiralbahn etwa 1/9 des Durchmessers der Erdkugel. Der Radius der Teilchenbahn beträgt also in etwa 700 km (707,89 km). Damit ergibt sich: e ⋅ B ⋅ r 1,6 ⋅ 10−19 ⋅ 5 ⋅ 10−6 ⋅ 700 ⋅ 103 m = m 1, 67 ⋅ 10−27 s m = 3, 353 ⋅ 108 s v = Damit wäre die Lichtgeschwindigkeit überschritten, d. h., die Protonen hätten relativistische Geschwindigkeiten, was nicht der Realität entspricht. d) Die Spiralbahn in der Ebene des Äquators entsteht aufgrund des inhomogenen Magnetfeldes. Bewegt sich das Teilchen in Richtung Äquator, wird die Flussdichte größer und damit die Bahn enger (kleinerer Radius). Deswegen bewegt sich das Teilchen wieder vom Äquator weg in Regionen, wo das Feld schwächer wird, was wiederum zu einer weiter werdenden Bahn führt. So entsteht eine spiralförmige Bahn, die um die Erde führt. M3 Mit Fehlern behaftet – magnetische Linsen Magnetische Linsen werden vor allem in Elektronenmikroskopen verwendet. Es handelt sich meist um kurze Zylinderspulen mit sehr hohen Flussdichten. Die Form des Magnetfeldes solcher Spulen entspricht dem Feld, das eine kreisförmige, stromdurchflossene Leiterschleife erzeugen würde. Die Bahnen von Elektronen, die eine solche Stromschleife senkrecht zu deren Fläche durchlaufen, sind kompliziert, da sie eine Spiralstruktur aufweisen. Interessanterweise treffen sich divergente Strahlen, die vor der Linse von einem Punkt ausgehen, hinter der Linse wieder in einem Punkt. Genau das macht die Linsenwirkung solcher Magnetfelder aus. Die räumliche Orientierung der Elektronenbahnen und die Entstehung starker Linsenfehler, die solchen Linsen anhaften, lassen sich mithilfe der Computersimulation demonstrieren. Im Gegensatz zu den vorherigen Simulationen dauert die Berechnung der einzelnen Elektronenbahnen jeweils einige Sekunden. Das liegt daran, dass die Berechnung des Magnetfeldes einer kreisförmigen Leiterschleife nach dem Biot-Savart-Gesetz zwar grundsätzlich möglich ist, am Ende jedoch Integrale entstehen, die analytisch nicht mehr lösbar sind. Daher muss in jedem Punkt der berechneten Elektronenbahn das jeweilige Magnetfeld in Richtung und Stärke durch numerisches Lösen der entsprechenden Integrale neu bestimmt werden, was Zeit kostet. Wenn Sie Genaueres dazu erfahren möchten, sind Sie auf den Anhang verwiesen. Am Ende der Station sollen die Lernenden einen Eindruck davon bekommen, wie eine Abbildung durch eine solche Magnetlinse aussehen würde, könnte man die Elektronenstrahlen als Lichtstrahlen auffassen. Eigenschaften von Magnetlinsen: Drehung und kissenartige Verzerrung der Bildebene Das Programm Magnetlinse_2.exe enthält eine Abbildungsmatrix, die durch ein spezielles Raytracing-Verfahren gewonnen wurde, welches jedem Punkt des Gegenstandes einen Punkt auf dem Bild zuweist, nachdem der Elektronenstrahl durch die Magnetlinse gegangen ist. Wendet man diese Abbildungsmatrix auf optische Bilder an, erkennt man wichtige Eigenschaften von Magnetlinsen, wie beispielsweise – die Drehung und – die kissenartige Verzerrung der Bildebene. Versuch: Schattenkreuzröhre als Ergänzung Falls in der Physiksammlung eine Schattenkreuzröhre vorhanden ist, können Sie die fokussierende Wirkung von Magnetfeldern auf Elektronenstrahlen auch experimentell zeigen, was sicher eine attraktive Ergänzung der Computersimulationen darstellt. Die Linsenwirkung einer kurzen Spule können Sie dann demonstrieren, indem Sie eine der beiden Helmholtzspulen so anordnen, wie in der nebenstehenden Abbildung dargestellt ist. Versuchsaufbau zur Schattenkreuzröhre Foto: M. Borchardt Versuchsbeobachtung Die divergenten Elektronenstrahlen erzeugen bei ausgeschaltetem Spulenstrom den Schatten eines Metallkreuzes auf dem Fluoreszenzschirm, der sich mit dem optischen Schatten deckt, den die hell leuchtende Glühwendel wirft. Beim Hochfahren des Spulenstroms erkennt man sehr schön, wie sich der elektronenoptische Schatten verkleinert und sich immer mehr dreht. Irgendwann kreuzen sich sogar die Elektronenstrahlen vor dem Schirm und erzeugen einen Schatten, der die typischen Linsenfehler von magnetischen Linsen zeigt. Lösungen 1. Siehe Mediothek. 2. b) Divergente Strahlen, die von einem Punkt auf der optischen Achse vor der Linse ausgehen (Beispiel 1), werden hinter der Linse wieder in einem Punkt auf der Achse vereinigt. Allerdings gilt das nur für Strahlen, welche die Linse nicht zu weit von der optischen Achse passieren, also für kleine Divergenzwinkel. Gehen die divergenten Strahlen von einem Punkt abseits der optischen Achse aus (Beispiel 2), treffen sie sich ebenfalls wieder in einem Punkt, dieser liegt jedoch gedreht gegenüber dem Ausgangspunkt. Im dritten Beispiel liegen die divergenten Strahlen alle in einer Ebene. Dadurch lässt sich gut erkennen, wie die Magnetlinse diese Bahnebene dreht. Parallele Strahlen (Beispiel 4) werden hinter der Linse fast wieder in einem Punkt vereinigt – allerdings verlaufen die Strahlen anders als Lichtstrahlen, die den Brennpunkt treffen und ihre Richtung beibehalten. Elektronenstrahlen bewegen sich zu einer Art Brennpunkt, bewegen sich dann aber wieder von diesem weg. 2. c) Recherche im Physikbuch oder im Internet. Bei Glaslinsen entsteht die chromatische Aberration aufgrund der verschiedenen Brechungseigenschaften von farbigem Licht. Blaues Licht wird von einer Linse stärker gebrochen als rotes, daher liegt der Brennpunkt für blaues Licht dichter an der Linse. Bei Magnetlinsen bewirken Schwankungen in der Elektronengeschwindigkeit, dass es verschiedene Brennpunkte gibt. Elektronen, die etwas schneller sind, werden später zu einem Brennpunkt geführt als langsamere Elektronen. Der Brennpunkt verwischt dadurch längs der Symmetrieachse der Linse. Die Magnetlinse verhält sich dabei umgekehrt wie die optische Linse. Weist man den Elektronen eine De-Broglie-Wellenlänge zu, dann haben schnelle Elektronen eine kleine Wellenlänge, entsprechen also dem blauen Licht in der Optik. Bei der Magnetlinse treffen sich diese Strahlen weit weg von der Linse, bei der Glaslinse nahe an der Linse. Daran sieht man, dass sich die Magnetlinsen nur sehr bedingt mit den Glaslinsen im Detail vergleichen lassen. 2. d) Beispiel Screenshot: Sphärische Aberration: Achsennahe Strahlen treffen sich in einem Punkt. Achsenferne Strahlen treffen sich ebenfalls, allerdings in einem anderen Punkt – die Brennweite hat sich geändert. Abbildungen zu 2. d) Sphärische Aberration Chromatische Aberration Beim Screenshot wurden folgende Einstellungen vorgenommen: Bahn 1: θ = 7, ϕ = 0, v = 25 Bahn 2: θ = −7, ϕ = 0, v = 25 Bahn 3: θ = 7, ϕ = 0, v = 22 Bahn 4: θ = −7, ϕ = 0, v = 22 2. e) Die einfachste Methode besteht darin, durch Blenden die Divergenz der Elektronenstrahlen stark zu begrenzen. Neuerdings versucht man auch, mit neuen Linsentypen die Fehler zu minimieren. 3. Beispiel: Screenshot aus dem Programm Magnetlinse_2.exe: M4 In der Krebstherapie eingesetzt – das Zyklotron Die Schüler erarbeiten sich grundlegende Eigenschaften eines klassischen Zyklotrons. Zur Veranschaulichung und als Arbeitsmittel dient die Computersimulation Zyklotron.exe, die eine Variation vieler Parameter ermöglicht. So lässt sich beispielsweise verdeutlichen, welchen Einfluss eine minimale Veränderung der Frequenz der Wechselspannung auf den Verlauf der Bahn der Teilchen hat. Da in der Sinuskurve dieser Spannung die Zeitintervalle markiert werden, in denen sich die Ladungen im Beschleunigungsspalt befinden, lässt sich schnell einsehen, warum das Zyklotron außer Takt gerät, wenn sich die Frequenz ändert. Darüber hinaus erlaubt die Simulation die Darstellung der Geschwindigkeits-Zeit- und Energie-Zeit-Kurve der beschleunigten Teilchen. Dies ist didaktisch wertvoll, denn die Lernenden bekommen so noch einmal vor Augen geführt, dass eine konstante, periodische Energiezufuhr (Beschleunigung im elektrischen Längsfeld) nicht zu einem linearen Anstieg der Geschwindigkeit führt. Diese Tatsache sollte den Schülern bereits beim Linearbeschleuniger begegnet sein. Lösungen 1. Siehe Mediothek. 3. Die Lorentzkraft wirkt im Zyklotron als Zentripetalkraft. Daher gilt: FL = FZ , also: q ⋅ v ⋅ B = und mit v = f = m ⋅ v2 , r 2π ⋅r = 2 π ⋅ r ⋅ f ergibt sich: T 1 q ⋅ ⋅B 2π m 4. Mit dem Schieberegler lässt sich die Frequenz der Beschleunigungsspannung um einige Prozent variieren. Schon bei 2 % Abweichung erkennt man im Diagramm der Wechselspannung (unteres Fenster), dass die Teilchen mit der Zeit den Beschleunigungsspalt zu immer ungünstigeren Zeitpunkten durchlaufen. Optimal wäre ein Passieren des Spalts, wenn die Spannung ihre Scheitelwerte hat. Irgendwann treffen die Teilchen den Beschleunigungsspalt in einer Phase, in der die Spannung so gepolt ist, dass sie bremst, anstatt zu beschleunigen. Die spiralförmige Bahn wird immer enger und die Teilchen bewegen sich nach einiger Zeit sogar wieder Richtung Zentrum, weil ihre Geschwindigkeit abnimmt. 5. Typische Geschwindigkeits- und Energiekurve eines Zyklotrons: Geschwindigkeitskurve Energiekurve Der Geschwindigkeitszuwachs pro Umlauf ist nicht konstant, während der Zuwachs an Energie bei jedem Passieren des Beschleunigungsspaltes gleich ist, denn dort wird den Teilchen stets die gleiche elektrische Energie zugeführt: Wel = q ⋅ E = q ⋅U , wobei d der Abstand der d Elektroden ist. Da die Geschwindigkeit in die kinetische Energie quadratisch eingeht, führt eine Verdopplung der Energie nur zum 2 -Fachen der Geschwindigkeit. Der Geschwindigkeitszuwachs folgt also einer Wurzelfunktion. 6. Da die Lorentzkraft als Zentripetalkraft wirkt, ergibt sich: v = q ⋅B ⋅r (vgl. 3.). m Eingesetzt in Ekin = 21 m ⋅ v 2 ergibt sich die gesuchte Formel: EkinEnd = q 2 ⋅ B2 ⋅ rEnd 2 . 2 ⋅m 7. Die Simulation zeigt, dass bei kleiner Beschleunigungsspannung die Teilchen sehr viele Umläufe machen müssen, um das Zyklotron zu verlassen. Da die Spannung klein ist, wird dem Teilchen im Beschleunigungsspalt nur wenig Energie zugeführt. Dafür durchläuft es den Spalt häufiger als bei hohen Spannungen und erhält schließlich die gleiche Endenergie, wie wenn die Beschleunigungsspannung hoch wäre. 8. Einstellungen: Ua = 2500 V, B = 0,1 T. Proton: Endgeschwindigkeit: v = 4,61⋅ 106 m , s Ekin = 0,5 ⋅ 1,673 ⋅ 10−27 ⋅ (4, 61⋅ 106 )2 J = 1, 778 ⋅ 10−14 J ≈ 111 keV Deuteron: Endgeschwindigkeit: v = 2,29 ⋅ 106 m , s Ekin = 0,5 ⋅ 3, 344 ⋅ 10−27 ⋅ (2, 29 ⋅ 106 )2 J = 8, 768 ⋅ 10−15 J ≈ 54, 73 keV Heliumkern: Endgeschwindigkeit: v = 2, 297 ⋅ 106 m , s Ekin = 0,5 ⋅ 6, 645 ⋅ 10−27 ⋅ (2,297 ⋅ 106 )2 J = 1, 753 ⋅ 10−14 J ≈ 109 keV 19 (1 J = 0,6242 • 10 eV) M5 Gekreuzte Felder – die Elektronenablenkröhre Die Elektronenablenkröhre ist ein vielseitiges Gerät, denn mit ihr lässt sich demonstrieren, wie sich Elektronen in einem elektrischen Querfeld ausbreiten, wie sie sich in einem homogenen Magnetfeld verhalten und was geschieht, wenn man beide Felder gleichzeitig einschaltet (gekreuzte Felder). Damit wird die Wirkungsweise eines Geschwindigkeitsfilters für geladene Teilchen verständlich und die darauf folgende Station vorbereitet, in der es um das Massenspektroskop geht. Die Computersimulation Elektronenablenkröhre.exe lässt alle Einstellungen zu, die auch das reale Experiment vorsieht, und bietet vielfältige Möglichkeiten, quantitative Aufgaben zu stellen, da sich die Bahn der Elektronen auch auf einem Koordinatensystem abbilden lässt. Ähnlich wie beim Fadenstrahlrohr ist es bei dieser Station hilfreich, wenn Sie die Elektronenablenkröhre vorher im Unterricht demonstriert haben und die Versuchsanordnung den Schülern während der Bearbeitung der Station zum Betrachten zugänglich machen. Lösungen 3. Einstellungen z. B.: Ua = 400 V , UK = 396 V , B = 0T . Damit ergibt sich eine Bahn, die durch den Punkt P(9 cm|2 cm) geht (d = 0,1 m). Einsetzen: y= UK 1 e UK 1 396 ⋅ (0, 09)2 ⋅ ⋅ ⋅ ⋅ x2 = ⋅ x2 = m = 0,02005m ≈ 2 cm 2 m d 2 ⋅ e ⋅U 4 ⋅ Ua ⋅ d 4 ⋅ 400 ⋅ 0,1 a m Damit ist die Formel bestätigt. 4. Die Ablenkspannung ist gleich 0. Nur das Magnetfeld ist eingeschaltet. a) Aus e ⋅ v 0 ⋅ B = m ⋅ v 02 m ⋅ v0 ergibt sich: r = . r e ⋅B b) Einstellungen z. B.: Ua = 400 V , UK = 0 V , B = 0,00337T . Damit ergibt sich eine Bahn, die durch den Punkt P(0 cm|4 cm) geht. Der Durchmesser der Kreisbahn beträgt also 4 cm, der Radius 2 cm. Rechnung: r= m ⋅ v0 = e ⋅B 5. a) 1,6 ⋅ 10−19 ⋅ 400 9,1⋅ 10−31 m = 0,020016m ≈ 2cm 1, 6 ⋅ 10−19 ⋅ 0,00337 9,1⋅ 10−31 ⋅ 2⋅ Einstellungen z. B.: Ua = 400 V , UK = − 1056 V , B = − 0,00089 T . Obere Ablenkplatte negativ, untere positiv; Magnetfeld aus der Papierebene auf den Betrachter zu gerichtet. 5. b) Die elektrische Feldkraft wird durch die Lorentzkraft kompensiert. Daher: FL = Fel ⇔ e ⋅ v ⋅ B = e ⋅ E 5. c) v = v = E . B E UK 1056 m m = = = 1,1865 ⋅ 107 (Werte aus Teil a) B B ⋅ d 0, 00089 ⋅ 0,1 s s Mit der eingestellten Beschleunigungsspannung Ua = 400 V ergibt sich: v = 2⋅ e ⋅ Ua = m 2⋅ 1, 6 ⋅ 10−19 m ⋅ 400 = 1,186 ⋅ 107 −31 9,1⋅ 10 s Damit ist die Formel v = E sehr gut bestätigt. B 5. d) Die Lorentzkraft ist im Gegensatz zur elektrischen Feldkraft von der Geschwindigkeit der Teilchen abhängig. Daher gilt (Einstellungen wie in Teilaufgabe a): – Langsame Elektronen spüren eine kleine Lorentzkraft Fel überwiegt. Daher werden diese Elektronen alle nach unten abgelenkt. Dies kann man überprüfen, indem man für Ua einen Wert einstellt, der kleiner ist als 400 V, was zu einer niedrigeren Geschwindigkeit als in Teil a) führt. – Schnelle Elektronen spüren eine größere Lorentzkraft FL überwiegt. Daher werden diese Elektronen alle nach oben abgelenkt. Dies kann man überprüfen, indem man für Ua einen Wert einstellt, der größer ist als 400 V, was zu einer höheren Geschwindigkeit als in Teil a) führt. M6 Wasserstoff und seine Isotope – das Massenspektroskop Vom didaktischen Standpunkt her ist das Massenspektroskop nach Bainbridge – im Vergleich zu vielen anderen Geräten zur Bestimmung der Masse atomarer Teilchen – für den Unterricht besonders geeignet, weil Sie hier die verschiedenen Abschnitte des Versuchsaufbaus klar und übersichtlich voneinander getrennt behandeln können. Dennoch ist es für Lernende kein einfaches Gerät. Die sachlogischen Zusammenhänge der einzelnen Komponenten stellen gewisse Anforderungen an das physikalische Verständnis. Als hilfreiches Werkzeug hat sich diesbezüglich die Computersimulation Massenspektroskop.exe erwiesen. Viele Aufgaben lassen sich durch Interaktion mit diesem Programm anschaulich erarbeiten. Lösungen 1. Siehe Mediothek. 3. Den Geschwindigkeitsfilter können nur Teilchen passieren, welche die Bedingung v = U E = K erfüllen. B1 B1 ⋅ d Im Ablenkfeld B2 gilt: q ⋅ v ⋅ B2 = m ⋅ v2 r m = q ⋅ B2 ⋅ r v Setzt man die Formel für die Geschwindigkeit ein, ergibt sich: m = q ⋅ B1 ⋅ B2 ⋅ d ⋅r . UK 4. Einstellungen z. B.: Ua = 180 V, UK = 29 V, B1 = 0, 00264 T, B2 = 0,0457T ; d = 0,06 m. Damit ergibt sich für Wasserstoff ein Bahndurchmesser im Ablenkfeld B2 von 0,085 m. Der Radius ist also 0,0425 m. Einsetzen: m = q ⋅ B1 ⋅ B2 ⋅ d 1,6 ⋅ 10−19 ⋅ 0,00264 ⋅ 0,0457 ⋅ 0, 06 ⋅ 0,0425 ⋅r = kg = 1,697 ⋅ 10−27 kg UK 29 Dies entspricht gut der Masse des Wasserstoffkerns (Proton m P = 1, 67 ⋅ 10−27 kg ). Für Experten: Wasserstoff und seine Isotope a) Tritium: Ua = 600 V, UK = 706 V, B1 = 0,06 T, B2 = 0,1361T Der Durchmesser der Teilchenbahn in Magnetfeld B2 ist dann: 0,09 m. 5. b) Deuterium: Ua = 400 V, UK = 706 V, B1 = 0,06 T, B2 = 0,1361T Der Durchmesser der Teilchenbahn in Magnetfeld B2 ist dann: 0,06 m. 5. c) Wasserstoff: Ua = 200 V, UK = 706 V, B1 = 0,06T, B2 = 0,1361 T Der Durchmesser der Teilchenbahn in Magnetfeld B2 ist dann: 0,03 m. Die Massen der Isotope verhalten sich in etwa wie 3 : 2 : 1. ANHANG Bewegte Ladungen im Computermodell – der Euler-Cauchy-Algorithmus Die Bahnkurven von geladenen Partikeln lassen sich Schritt für Schritt berechnen, wenn man den Betrag und die Richtung der Kräfte kennt, die in den verschiedenen Punkten der Bahn auf die Teilchen wirken. Für den eindimensionalen Fall stellt sich das beispielsweise so dar: Der Startpunkt xStart und die Startgeschwindigkeit vStart sind bekannt. Aus a = dv folgt der Geschwindigkeitszuwachs dv = a ⋅ dt und dt aus v = dx folgt der Wegzuwachs dx = v ⋅ dt . dt Damit ergibt sich folgende Iterationsschleife: x = x Start ; v = v Start ; t := 0 ; repeat; a(x, v) = F(x, v) m v neu = v alt + a(x, v) ⋅ dt x neu = x alt + v neu ⋅ dt t neu = t alt + dt Zeichne x gegen t until t > t End Bei einer Bewegung im Raum muss dieses Verfahren für jede Raumrichtung durchgeführt werden, was voraussetzt, dass die Kraftkomponenten in x-, y- und z-Richtung formelmäßig bekannt sind. Das oben beschriebene Verfahren wird auch Euler-Cauchy-Algorithmus genannt und stellt die einfachste Möglichkeit dar, die Bewegung von Teilchen numerisch zu berechnen. Sind die Simulationszeiträume nicht zu groß und der Zeitschritt dt möglichst klein, liefert das Verfahren recht gute Ergebnisse. Rundungsfehler aufgrund starker Bahnkrümmungen In manchen Fällen, besonders dann, wenn die Bahnen sehr starke Krümmungen aufweisen, schaukeln sich jedoch Rundungsfehler mit der Zeit enorm auf. Deshalb sollte man hier auf Verfahren zurückgreifen, die Zwischenwerte im betrachteten Zeitintervall ausrechnen, die ein Wegdriften der berechneten Größen vom Sollwert verhindern. Typische Beispiele solcher Algorithmen sind das Runge-Kutta-Verfahren zweiter Ordnung, was noch recht überschaubar ist, und das Runge-Kutta-Verfahren vierter Ordnung, das bereits einen hohen Programmieraufwand erfordert – dafür aber auch sehr exakte Simulationsläufe liefert. Das Magnetfeld einer kreisförmigen Leiterschleife Mit dem Biot-Savart-Gesetz lassen sich durch Integration längs des Leiters L alle Magnetfeldanteile so aufaddieren, dass man das Magnetfeld im Punkt P in Betrag und Richtung erhält: ur ur µ B r = 0 ⋅I⋅ ∫ 4π L ( ) r ur uur dl × r − rL r ur 3 r − rL Mithilfe dieses Gesetzes soll das Magnetfeld einer kreisförmigen, stromdurchflossenen Leiterschleife in jedem x r beliebigen Beobachtungspunkt r = y berechnet werden. z Dazu legen wir die Leiterschleife in die y-z-Ebene eines kartesischen Koordinatensystems und parametrisieren den Weg längs der Leiterschleife mithilfe von Polarkoordinaten wie folgt: Für einen Punkt auf dem Leiter gilt: 0 0 uur rL = y L = R ⋅ cos(φ) z R ⋅ sin(φ) L uur Leiten wir den Vektor rL nach φ ab, erhalten wir: ur 0 drL = R ⋅ − sin(φ) dφ cos(φ) uur Der rechte Vektor entspricht aber gerade dem Einheitsvektor eφ , der die Lage des Winkels φ im Koordinatensystem beschreibt, sodass wir schreiben können: ur uur drL = R ⋅ eφ dφ ur Der Differenzvektor drL entspricht dem infinitesimalen Leiterstück r dl im Biot-Savart-Gesetz und daher gilt: ur uur r uur dl = R ⋅ eφ bzw. dl = R ⋅ d φ ⋅ eφ dφ r Setzen wir das Element dl ins Biot-Savart-Gesetz ein und be- rücksichtigen wir, dass wir die gesamte Länge des Leiters erfas- sen, wenn wir den Winkel φ von 0 bis 2π laufen lassen, nimmt das Gesetz die Form an: 2π ur ur µ B r = 0 ⋅I⋅ ∫ 4π 0 ( ) r ur uur r − rL R⋅ dφ ⋅ e ur 3 φ × r r − rL Etwas übersichtlicher sortiert, erhalten wir schließlich das Biot-Savart-Gesetz für das Magr netfeld eines Kreisstroms an jedem beliebigen Beobachtungspunkt r : 2π ur ur µ B r = 0 ⋅I ⋅ R⋅ ∫ 4π 0 ( ) r ur uur e × r − rL r ur 3 φ r − rL dφ Wir wählen die folgende Situation: Die Leiterschleife liegt in der y-z-Ebene, hat den Radius R und wird vom Strom I durchflossen. Für die Terme in der oberen Formel (Integral) ergeben sich dann folgende Beziehungen, die oben zwar bereits genannt wurden, hier aber noch einmal im Zusammenhang dargestellt werden sollen: Der Beobachtungspunkt, also die Stelle, an der wir das Magnetfeld berechnen wollen, hat x 0 r uur den Ortsvektor r = y . Ein Punkt auf der Leiterschleife wird durch den Ortsvektor rL = y L z z L erreicht, den wir mithilfe von Polarkoordinaten so ausdrücken können: 0 0 uur rL = y L = R ⋅ cos(φ) . z R ⋅ sin(φ) L uur Der Einheitsvektor eϕ , der den Winkel ϕ beschreibt, ist dann: 0 uur eφ = − sin(φ) . cos(φ) r ur Der Differenzvektor r − rL ist vom Punkt auf der Leiterschleife zum Beobachtungspunkt hin x r ur gerichtet und wird zu: r − rL = y − R ⋅ cos(φ) . z − R ⋅ sin(φ) r ur Der Betrag dieses Vektors ist: r − rL = x 2 + (y − R ⋅ cos(φ))2 + (z − R ⋅ sin(φ))2 . Das Kreuzprodukt im Integral des Biot-Savart-Gesetzes nimmt dann die folgende Form an: 0 x − sin(φ) ⋅ (z − R ⋅ sin(φ)) − cos(φ) ⋅ (y − R ⋅ cos(φ)) uur r r eφ × (r − r L ) = − sin(φ) × y − R ⋅ cos(φ) = x ⋅ cos(φ) cos(φ) z − R ⋅ sin(φ) x ⋅ sin(φ) − sin(φ) ⋅ z + R ⋅ sin 2 (φ)) − cos(φ) ⋅ y + R ⋅ cos2 (φ)) − sin(φ) ⋅ z − cos(φ) ⋅ y + R = x ⋅ cos(φ) x ⋅ cos(φ) = x ⋅ sin(φ) x ⋅ sin(φ) Setzt man dies in das Integral ein, erhält man für jede der drei Raumrichtungen die Stärke des Magnetfeldes im Punkt P in Form der Integrale: Bx = By = Bz = µ0 ⋅ I ⋅R⋅ 4π 2π µ0 ⋅I ⋅R⋅ 4π 2π µ0 ⋅I⋅R⋅ 4π 2π ∫ 0 ∫ 0 ∫ 0 R − z ⋅ sin(φ) − y ⋅ cos(φ) ( 2 x + (y − R ⋅ cos(φ)) + (z − R ⋅ sin(φ)) ) ( x + (y − R ⋅ cos(φ))2 + (z − R ⋅ sin(φ))2 ) ( 2 2 x ⋅ cos(φ) 2 x ⋅ sin(φ) ) x 2 + (y − R ⋅ cos(φ))2 + (z − R ⋅ sin(φ))2 3 dφ 3 dφ 3 dφ Diese Integrale lassen sich analytisch nicht lösen. Daher müssen sie auf numerischem Weg (Computer) näherungsweise bestimmt werden. Um beispielsweise die Bahn eines geladenen Teilchens durch das Magnetfeld einer kreisförmigen Leiterschleife zu simulieren, muss für jeden durch Iteration bestimmten Punkt der Bahn Stärke und Richtung des Magnetfeldes durch die drei obigen Integrale numerisch berechnet werden. Dies stellt einen erheblichen Rechenaufwand dar, der sich in der Ausführungsgeschwindigkeit einer solchen Simulation niederschlägt. Ergänzung: Interessant ist der Spezialfall, wenn man sich nur für das Magnetfeld genau auf der Achse der Linse (hier der x-Achse) interessiert. Dort sind die y- und z-Koordinaten des Beobachtungspunktes 0, sodass die oberen Integrale sich enorm vereinfachen zu: Bx = = µ0 ⋅ I ⋅R⋅ 4π 2π µ0 ⋅I ⋅ R⋅ 4π 2π ∫ 0 ∫ 0 = µ0 ⋅I ⋅R⋅ 4π µ0 ⋅I ⋅R⋅ 4π 2π By = µ0 ⋅I⋅R⋅ 4π 2π Bz = R ( x 2 + (R ⋅ cos(φ))2 + (R ⋅ sin(φ))2 R ( x 2 + R2 R ( x 2 + R2 ∫ 0 ∫ 0 ( ( ) 3 ) dφ = 3 ⋅ 2π = µ0 ⋅ I ⋅ x ⋅ cos(φ) x 2 + R2 ) x ⋅ sin(φ) x 2 + R2 µ0 ⋅I⋅R⋅ 4π ) dφ = 3 dφ = 3 2⋅ µ0 ⋅I ⋅ R⋅ 4π dφ 2π R ( x 2 + R2 R2 ( µ0 ⋅ I ⋅R⋅ 4π ) 3 x 2 + R2 ( ( ) x 2 + R2 x 2 + R2 ∫ dφ 0 3 x x ) ⋅ 3 2π ) 3 ⋅ ∫ cos(φ) d φ = 0 0 2π ) 3 ⋅ ∫ sin(φ) d φ = 0 0 Übrig bleibt also nur die Komponente Bx mit: Bx = µ 0 ⋅ I ⋅ 2⋅ ( R2 x 2 + R2 ) 3 Diese bekannte Formel findet man in der Literatur sehr häufig, wenn nach dem Magnetfeld einer kreisförmigen Leiterschleife sucht. Allerdings erhält man damit lediglich das Magnetfeld auf der x-Achse.