Document

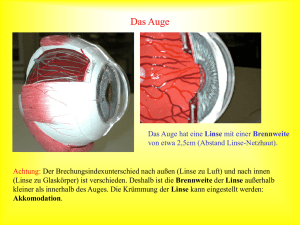
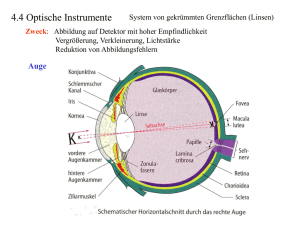
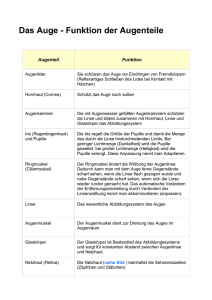
21.4 Linsen
Eine Linse ist ein optisches Gerät, dessen Funktion auf dem
Brechungsgesetz beruht. Dadurch erfährt der Lichtstrahl eine
Richtungsänderung beim Ein- und Austritt. Die Oberflächen von Linsen
sind im allgemeinen sphärisch geformt. Der Krümmungsradius und der
Brechungsindex des Materials, aus dem die Linse besteht, bestimmt die
Brechungseigenschaften der Linse.
Betrachten wir zunächst den Strahlengang beim Durchgang durch eine
planparallele Glasplatte. Eine solche Glasplatte ist gewissermaßen eine
Linse mit unendlichem Krümmungsradius auf beiden Seiten.
Nach dem Brechungsgesetz von Snellius
hat der ausfallende Strahl die gleiche Richtung
wie der einfallende Strahl, die Strahl ist lediglich
parallel verschoben.
Entscheidend für die Funktion einer Linse ist
daher, dass die beiden Oberflächen zueinander
gekrümmt sind.
α1
α2
n1
α2
n2
α1
n1
Wir unterscheiden zwischen konvex geschliffenen Sammellinsen und
konkav geschliffenen Zerstreuungslinsen. Wenn der Krümmungsradius
der sphärischen Oberfläche groß ist gegen die Dicke der Linse, so
spricht man von einer dünnen Linse. In diesem Fall kann man eine
vereinfachte Bildkonstruktion vornehmen, indem man annimmt, dass die
Brechung in einer einzigen Ebene, der Hauptebene der Linse erfolgt.
Sammellinse
Zerstreuungslinse
F
F
F
F
Hauptebene
Fällt ein achsenparalleles Strahlenbündel auf eine Sammellinse, so
werden die Strahlen zum Brennpunkt auf der Transmissionsseite
fokussiert.
Achsenparallele Strahlen, die auf eine Zerstreuungslinse treffen, werden
von der optischen Achse weg gebrochen. Ihre rückwärtigen
Verlängerungen vereinigen sich im Brennpunkt auf der Einfallsseite.
Neben der Brennweite f benutzt man zur Charakterisierung einer Linse
auch die Brechkraft D, die als der Kehrwert der Brennweite definiert ist:
1
D=
Einheit : [D ] = 1 m −1 = 1 dpt (Dioptrie)
f
Brennebene einer Sammellinse
Jedes parallel einfallende Strahlenbündel
wird in einen Punkt in der Brennebene
fokussiert. Die Brennebene ist die zur
Hauptebene parallel verlaufende Ebene,
die die optische Achse im Brennpunkt
schneidet. (Speziell: das achsenparallele
Strahlenbündel wird in den Brennpunkt
fokussiert.)
Hauptebene
Brennebene
F
Bildkonstruktion bei der Sammellinse
Für die Bildkonstruktion bei der Sammellinse gelten folgende Regeln:
•
Der Mittelpunktstrahl, der durch den Schnittpunkt von Hauptachse
und optischer Achse verläuft, wird nicht gebrochen.
•
Der achsenparallele Strahl wird durch den jenseitigen Brennpunkt F‘
gebrochen
•
Der Brennpunktstrahl verläuft durch den Brennpunkt auf der
Einfallsseite und verlässt die Linse achsenparallel.
Mittelpunktstrahl
Der Bildpunkt liegt dann
im Schnittpunkt der
gebrochenen Strahlen.
G
achsenparalleler Strahl
F
F‘
g
b
f
Brennpunktstrahl
B
Wir erinnern uns an die Definition des
Abbildungsmaßstabes:
sowie an die Abbildungsgleichung:
V=
1 1 1
fg
= + ⇒b=
f g b
g −f
und diskutieren drei mögliche Fälle für die
Sammellinse:
1) g > 2f Æ -1 < V < 0, b > 0
F
Æ reelles, verkleinertes, umgedrehtes Bild
2) f < g < 2f Æ V < -1, b > 0
Æ reelles, vergrößertes, umgedrehtes Bild
B
b
=−
G
g
F
3) 0 < g < f Æ V > 1, b < 0
Æ virtuelles, vergrößertes, aufrechtes Bild
F
Bildkonstruktion der Zerstreuungslinse
Bei der Zerstreuungslinse gibt es auf der Transmissionsseite keinen
Schnittpunkt der gebrochenen Strahlen. Es gibt also kein reelles Bild,
sondern es entsteht ein virtuelles Bild am Ort, wo sich die rückwärtigen
Verlängerungen der gebrochenen Strahlen treffen.
•
Der Mittelpunktstrahl verlässt die Linse ohne Richtungsänderung.
•
Der achsenparallele Strahl wird so gebrochen, dass seine
rückwärtige Verlängerung durch den Brennpunkt auf der Einfallsseite
läuft.
•
Der auf den Brennpunkt auf der Transmissionsseite gerichtete Strahl
verlässt die Linse achsenparallel.
F‘
F
Abbildungsfehler
Linsen weisen bestimmte Abbildungsfehler auf, die prinzipieller Natur
sind und auch bei perfekter Herstellung der Linsen auftreten.
Achsenferne Strahlen werden nicht in einem einzigen Brennpunkt
fokussiert, sondern näher an der Linse. Man bezeichnet dies als
sphärische Aberration. Sie kann
vermindert werden, indem man
achsenferne Strahlen ausblendet,
man verliert dann jedoch an Lichtstärke.
Da der Brechungsindex leicht von der
Wellenlänge abhängig ist, kommt es in
der Linse zur Dispersion. Die
verschiedenfarbigen Anteile des weißen
Lichts werden also nicht in den selben
Punkt fokussiert. Diesen Effekt bezeichnet
man als chromatische Aberration.
Beide Effekte lassen sich durch Verwendung von Korrekturlinsen
weitgehend beheben.
22. Optische Systeme
22.1 Das Auge
Die Augenlinse funktioniert wie eine Sammellinse, die das einfallende
Licht auf die Netzhaut fokussiert. Der Abstand zwischen Linse und
Netzhaut beträgt etwa 25 mm, dies entspricht der maximalen Brennweite
der Linse. Objekte, die im „Unendlichen“ stehen (paralleler Lichteinfall)
werden also auf die Netzhaut fokussiert. Befindet sich der Gegenstand
näher am Auge, kann die Brennweite der Linse durch Anspannung des
Ziliarkuskels verkleinert werden,
um ein scharfes Bild auf der
Netzhaut zu erzeugen
(Akkomodation).
Der minimal Abstand, bei dem
dies möglich ist, ist die deutliche
Sehweite s0, die bei jedem
Mensch anders ist und vom
Alter abhängt. Als Bezugswert
werden s0 = 25 cm festgelegt.
Das Objekt befindet sich dann
am so genannten Nahpunkt.
Weitsichtigkeit
Weitsichtigkeit liegt vor, wenn nur weit entfernte Gegenstände scharf
wahrgenommen werden können. Die Lichtstrahlen, die von näher am
Auge liegenden Gegenständen ausgehen, können von der Augenlinse
nicht ausreichend gebrochen werden und werden hinter der Netzhaut
fokussiert. Diese Sehstörung kann durch eine Sammellinse
ausgeglichen werden.
Kurzsichtigkeit
Das kurzsichtige Auge kann weit entfernte Gegenstände nicht scharf
wahrnehmen, da selbst die völlig entspannte Augenlinse eine zu große
Brechkraft hat. Die Lichtstrahlen werden vor der Netzhaut fokussiert.
Kurzsichtigkeit kann durch eine Zerstreuungslinse ausgeglichen werden.
Sehwinkel
Die Größe, mit der ein Gegenstand vom Auge wahrgenommen wird, ist
durch die Größe des Bildes auf der Netzhaut gegeben. Wir können dies
durch den so genannten Sehwinkel ε ausdrücken. Je näher ein
Gegenstand gegebener Größe G sich am Auge befindet, umso größer
ist das Bild auf der Netzhaut und damit der entsprechende Sehwinkel.
G
ε1
g1
G
ε2
25 mm
ε2
ε1
B1
B2
Für kleine Winkel gilt:
ε=
B
25 mm
bzw.
ε=
G
g
⇒ B = 25 mm ⋅
G
g
22.2 Die Lupe
Eine Lupe dient dazu, kleine Gegenstände größer wahrnehmen zu
können, als dies bei gegebener deutlicher Sehweite der Fall wäre.
Befindet sich der Gegenstand am
Nahpunkt, also in einem Abstand vom
Auge, der der deutlichen Sehweite s0
entspricht, dann ergibt sich der
maximale Sehwinkel ε0, unter dem der
Gegenstand vom bloßen Auge noch
scharf wahrgenommen werden kann:
ε0 =
G
ε0
ε0
s0
Lupe
G
ε
ε
f
G
s0
Eine Lupe ist eine Sammellinse mit Brennweite f. Hält man eine Lupe vor
das Auge und bringt den Gegenstand in ihre Brennebene, so werden die
vom Gegenstand ausgehenden Lichtstrahlen von der Lupe in parallele
Lichtbündel gebrochen, und erscheinen dem Auge als virtuelles Bild, das
im Unendlichen steht. Dieses Bild kann vom Auge mühelos abgebildet
werden.
Der Sehwinkel, unter dem der Gegenstand mit Verwendung der Lupe
wahrgenommen wird, ist dann
ε=
G
f
Man definiert die Vergrößerung vL einer Lupe mit Brennweite f als den
den Sehwinkel ε unter Verwendung der Lupe geteilt durch den
Sehwinkel ε0, unter dem der Gegenstand im Abstand der deutlichen
Sehweite mit bloßem Auge wahrgenommen werden kann:
vL =
ε s0
=
ε0 f
Die Vergrößerung ist nicht zu verwechseln mit dem Abbildungsmaßstab
V = B/G = -b/g, der eine Kenngröße der Linse ist. Die Vergrößerung ist
bezogen auf die durchschnittliche Leistungsfähigkeit des bloßen Auges,
der eine Konvention zugrunde liegt, nämlich die deutliche Sehweite s0.
In der Praxis können höhere Vergrößerungen erzielt werden, wenn der
Gegenstand näher an die Linse herangebracht wird. Dann erscheint der
Gegenstand dem Auge aber nicht mehr im Unendlichen, das Auge muss
akkomodieren.
22.3 Das Mikroskop
Ein Mikroskop dient dazu, sehr kleine Gegenstände für das Auge
sichtbar zu machen. Ein Mikroskop ist im einfachsten Fall ein System
von zwei Sammellinsen.
Der Gegenstand G befindet sich
dicht vor dem Brennpunkt der ersten
Sammellinse, dem so genannten
Objektiv. Das Objektiv erzeugt ein
reelles Zwischenbild B am Ort der
Brennebene der zweiten
Sammellinse, dem Okular.
Objektiv
fOb
G
Okular
t
fOk
β
β
B
Das Okular funktioniert wie eine Lupe, durch die das reelle Zwischenbild
betrachten werden kann. Da das Zwischenbild in der Brennebene des
Okulars steht, treffen die vom Zwischenbild ausgehenden Lichtstrahlen
als parallele Lichtbündel auf das Auge des Betrachters, das Bild
erscheint dem Betrachter also aus dem Unendlichen stehend und kann
mühelos von der Augenlinse auf die Netzhaut abgebildet werden.
Den Abstand zwischen der Brennebene des Objektivs und der
Brennebene des Okulars bezeichnet man als die Tubuslänge t des
Mikroskops. Ein typischer Wert ist t = 16 cm.
Für das Objektiv gilt:
tan β =
G
B
=−
fOb
t
Damit folgt für den Abbildungsmaßstab des Objektivs:
VOb =
B
t
=−
G
fOb
Für die Vergrößerung des Okulars (Lupe) gilt:
v Ok =
s0
fOk
Daraus erhält man die Vergrößerung des Mikroskops:
v M = VOb ⋅ v Ok = −
t
fOb
⋅
s0
fOk
Beispiel zum Mikroskop: Die Brennweite des Objektivs betrage
fOb = 1,2 cm, die Brennweite des Okulars fOk = 2 cm. Der Abstand der
beiden Linsen beträgt 20 cm. Wie groß ist die Vergrößerung des
Mikroskops?
Die Tubuslänge t ist der Abstand der Brennebenen von Objektiv und
Okular, also
t = 20 cm − fOb − fOk = 20 cm − 1,2 cm − 2 cm = 16,8 cm
Damit ergibt sich für die Vergrößerung
vM = −
t ⋅ s0
16,8 cm ⋅ 25 cm
=−
= −175
fOb ⋅ fOk
1,2 cm ⋅ 2 cm